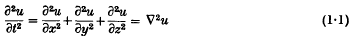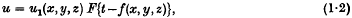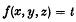Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ludwig, Donald
1960.
Exact and asymptotic solutions of the cauchy problem.
Communications on Pure and Applied Mathematics,
Vol. 13,
Issue. 3,
p.
473.
Cooper, Jr., Henry F.
1967.
Propagation of One-Dimensional Waves in Inhomogeneous Elastic Media.
SIAM Review,
Vol. 9,
Issue. 4,
p.
671.
Yen, David H. Y.
and
Bazer, J.
1967.
The riemann matrix of (2 + 1)‐dimensional symmetric‐hyperbolic systems.
Communications on Pure and Applied Mathematics,
Vol. 20,
Issue. 2,
p.
329.
Moodie, T. Bryant
1973.
On the propagation, reflection, and transmission of transient cylindrical shear waves in nonhomogeneous four-parameter viscoelastic media.
Bulletin of the Australian Mathematical Society,
Vol. 8,
Issue. 3,
p.
397.
Barclay, D.W.
and
Moodie, T. Bryant
1974.
Verifications of a formal technique for viscoelastodynamics.
Bulletin of the Australian Mathematical Society,
Vol. 11,
Issue. 2,
p.
279.
Moorhem, William K. Van
and
George, A. R.
1975.
On the stability of plane shocks.
Journal of Fluid Mechanics,
Vol. 68,
Issue. 01,
p.
97.
Moodie, T. B.
and
Barclay, D. W.
1975.
Wave propagation in inhomogeneous variable-section viscoelastic bars.
Acta Mechanica,
Vol. 23,
Issue. 3-4,
p.
199.
Moodie, T. Bryant
and
Barclay, D. W.
1976.
Transient solutions for longitudinally impacted inhomogeneous conical shells.
Journal of Elasticity,
Vol. 6,
Issue. 2,
p.
209.
Collins, C. B.
1976.
Complex potential equations I. A technique for solution.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 80,
Issue. 1,
p.
165.
Moodie, T. B.
and
Barclay, D. W.
1977.
Wave propagation from a cylindrical cavity.
Acta Mechanica,
Vol. 27,
Issue. 1-4,
p.
103.
Urbantke, H.
1979.
On rotating plane-fronted waves and their Poincaré-invariant differential geometry.
Journal of Mathematical Physics,
Vol. 20,
Issue. 9,
p.
1851.
Collins, C. B.
1980.
All solutions to a nonlinear system of complex potential equations.
Journal of Mathematical Physics,
Vol. 21,
Issue. 2,
p.
240.
1982.
Bäcklund Transformations and Their Applications.
Vol. 161,
Issue. ,
p.
302.
Szekeres, Peter
1983.
Solutions of Einstein’s equations involving arbitrary functions.
Journal of Mathematical Physics,
Vol. 24,
Issue. 12,
p.
2786.
Urbantke, H.
1985.
On complex-valued scalar waves of the simply- progressive type.
Reports on Mathematical Physics,
Vol. 21,
Issue. 1,
p.
111.
Singh, Avtar
and
Gupta, Kishan Chand
1986.
One-dimensional propagation of discontinuities in non-homogeneous linear viscoelastic semi-infinite media.
Sadhana,
Vol. 9,
Issue. 1,
p.
1.
KANEKO, Jyoichi
1986.
WAVE EQUATION AND DUPIN HYPERSURFACE.
Memoirs of the Faculty of Science, Kyushu University. Series A, Mathematics,
Vol. 40,
Issue. 1,
p.
51.
Ward, R S
1987.
Progressing waves in flat spacetime and in plane-wave spacetimes.
Classical and Quantum Gravity,
Vol. 4,
Issue. 3,
p.
775.
Torrence, R. J.
and
Couch, W. E.
1988.
Progressing waves on spherical spacetimes.
General Relativity and Gravitation,
Vol. 20,
Issue. 4,
p.
343.
1989.
Methods of Mathematical Physics.
p.
799.