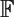Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T13:51:03.500Z Has data issue: false hasContentIssue false
  • English
  • Français

Simply transitive quaternionic lattices of rank 2 over $\mathbb{F}$q(t) and a non-classical fake quadric

Published online by Cambridge University Press:  20 March 2017

JAKOB STIX  and
ALINA VDOVINA
JAKOB STIX
Affiliation:
Institut für Mathematik, Goethe-Universität, 60325 Frankfurt am Main, Germany. e-mail: stix@math.uni-frankfurt.de
ALINA VDOVINA
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU. e-mail: Alina.Vdovina@newcastle.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

By means of a quaternion algebra over 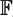$\mathbb{F}$q(t), we construct an infinite series of torsion free, simply transitive, irreducible lattices in PGL2(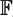$\mathbb{F}$q((t))) × PGL2(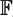$\mathbb{F}$q((t))). The lattices depend on an odd prime power q = pr and a parameter τ ∈ 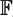$\mathbb{F}$q×, τ ≠ 1, and are the fundamental group of a square complex with just one vertex and universal covering Tq+1 × Tq+1, a product of trees with constant valency q + 1.

Our lattices give rise via non-archimedian uniformization to smooth projective surfaces of general type over 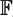$\mathbb{F}$q((t)) with ample canonical class, Chern numbers c12 = 2 c2, trivial Albanese variety and non-reduced Picard scheme. For q = 3, the Zariski–Euler characteristic attains its minimal value χ = 1: the surface is a non-classical fake quadric.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 3 , November 2017 , pp. 453 - 498
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BB95] Ballmann, W. and Brin, M. Orbihedra of nonpositive curvature. Inst. Hautes Etudes Sci. Publ. Math. 82 (1995), 169–209.Google Scholar
[BB12] Böckle, G. and Butenuth, R. On computing quaternion quotient graphs for function fields. J. Théor. Nombres Bordeaux. 24 (2012), no. 1, 73–99.Google Scholar
[BCG05] Bauer, I.C., Catanese, F. and Grunewald, F. The classification of surfaces with pg = q =0 isogenous to a product of curves. Pure Appl. Math. Q. 4 Special Issue: In honor of Fedor Bogomolov Part 1, (2008), no. 2, 547–586.Google Scholar
[Be96] Beauville, A. Complex algebraic surfaces. translated from the 1978 French original by R. Barlow, with assistance from Shepherd–Barron, N. I. and Reid, M. London Mathematical Society Student Texts 34 (2nd ed.) (Cambridge University Press), 1996, x+132 pp.Google Scholar
[Bh98] Behr, H. Arithmetic groups over function fields I. A complete characterization of finitely generated and finitely presented arithmetic subgroups of reductive algebraic groups. J. Reine Angew. Math. 495 (1998), 79–118.CrossRefGoogle Scholar
[Bl03] Blumenthal, O. Über Modulfunktionen von mehreren Veränderlichen. Math. Ann. 56 (1903), 509–548.Google Scholar
[BM97] Burger, M. and Mozes, Sh. Finitely presented simple groups and products of trees. C. R. Acad. Sci. Paris Sér. I Math. 324 (1997), no. 7, 747–752.CrossRefGoogle Scholar
[BM00] Burger, M. and Mozes, Sh. Lattices in product of trees. Inst. Hautes Études Sci. Publ. Math. 92 (2000), 151–194.Google Scholar
[CFH] Chinburg, T., Friedlander, H., Howe, S., Kosters, M., Singh, B., Stover, M., Zhang, Y. and Ziegler, P. Presentations for quaternionic S-unit groups. Experimental Mathematics. 24 (2015), no. 2, 175–182.Google Scholar
[Di22] Dickson, L.E. Arithmetic of quaternions. Proc. London Math. Soc. (2) 20 (1922), 225–232.Google Scholar
[Di58] Dickson, L.E. Linear groups : With an exposition of the galois field theory. With an introduction by Magnus, W. (Dover Publications, Inc., New York 1958), xvi+312 pp.Google Scholar
[Dz14] Džambić, A. Fake quadrics from irreducible lattices acting on the product of upper half planes. Math. Ann. 360 (2014), no. 1-2, 23–51.Google Scholar
[GN95] Gekeler, E.-U. and Nonnengardt, U. Fundamental domains of some arithmetic groups over function fields. Internat. J. Math. 6 (1995), 689–708.Google Scholar
[Ha02] Hatcher, A. Algebraic Topology (Cambridge University Press, 2002), 554 pp.Google Scholar
[He54] Herrmann, O. Eine metrische Charakterisierung eines Fundamentalbereiches der Hilbertschen Modulgruppen. Math. Z. 60 (1954), 148–155.Google Scholar
[Hi56] Hirzebruch, F. Automorphe Formen und der Satz von Riemann-Roch, in: Symposium internacional de topologí a algebraica. Univ. Nacional Autónoma de México and UNESCO (Mexico City, 1958), 129–144.Google Scholar
[Hi87] Hirzebruch, F. Gesammelte Abhandlungen, Band I, 1951–1962 (Springer-Verlag, Berlin, 1987), viii+814 pp.Google Scholar
[KW80] Kirchheimer, F. and Wolfart, J. Explizite Präsentation gewisser Hilbertscher Modulgruppen durch Erzeugende und Relationen. J. Reine Angew. Math. 315 (1980), 139–173.Google Scholar
[LPS88] Lubotzky, A., Phillips, R. and Sarnak, P. Ramanujan graphs. Combinatorica. 8 (1988), no. 3, 261–277.Google Scholar
[LSV15] Linowitz, B., Stover, M. and Voight, J. Fake quadrics, preprint (2015), arXiv: 1504.04642.Google Scholar
[Ma40] Maass, H. Über Gruppen von hyperabelschen Transformationen. Sitzungsber. Heidelberg Akad. Wiss. Math.-nat. Klasse 2 (1940).Google Scholar
[Ma91] Margulis, G. A. Discrete subgroups of semisimple Lie groups. Ergeb. Math. Grenzgeb. (3), volume 17 (Springer-Verlag, Berlin, 1991), x+388 pp.Google Scholar
[Mo94] Morgenstern, M. Existence and explicit constructions of q + 1 regular Ramanujan graphs for every prime power q . J. Combin. Theory Ser. B 62 (1994), no. 1, 44–62.Google Scholar
[Mo95] Mozes, Sh. Actions of Cartan subgroups. Israel J. Math. 90 (1995), no. 1–3, 253–294.Google Scholar
[Mu79] Mumford, D. An algebraic surface with K ample, (K 2) = 9, pg = q = 0. Amer. J. Math. 101 (1979), no. 1, 233–244.Google Scholar
[Pa11] Papikian, M. On finite arithmetic simplicial complexes. Proc. Amer. Math. Soc. 139 (2011), no. 1, 111–124.Google Scholar
[Pr89] Prasad, G. Volumes of S-arithmetic quotients of semi-simple groups. Publ. Math. IHES 69 (1989), 91–117.CrossRefGoogle Scholar
[Ra04] Rattaggi, D.A. Computations in Goups acting on a product of trees: normal subgroup structures and quaternion lattices. Thesis ETH Zürich (2004).Google Scholar
[Ru17] Rungtanapirom, N. Quaternionic arithmetic lattices of rank 2 and a fake quadric in characteristic 2. Thesis Goethe–Universität Frankfurt (2017).Google Scholar
[Se80] Serre, J.-P. Trees, translated from the French by Stillwell, John (Springer, 1980), ix+142pp.Google Scholar
[Sh78] Shavel, I.H. A class of algebraic surfaces of general type constructed from quaternion algebras. Pacific J. Math. 76 (1978), no. 1, 221–245.Google Scholar
[Sw71] Swan, R.G. Generators and relations for certain special linear groups. Adv. Math. 6 (1971), 1–77.Google Scholar
[Vi80] Vignéras, M.-F. Arithmétique des algèbres de quaternions. Lecture Notes in Math. 800 (Springer-Verlag, Berlin Heidelberg, 1980).Google Scholar
[VM80] Valentini, R.C. and Madan, M. L. A Hauptsatz of L. E. Dickson and Artin-Schreier extensions. J. Reine Angew. Math. 318 (1980), 156–177.Google Scholar
[Vo09] Voight, J. Computing fundamental domains for Fuchsian groups. J. Théor. Nombres Bordeaux 21 (2009), no. 2, 469–491.Google Scholar
[Wi96] Wise, D. Non-positively curved squared complexes, aperiodic tilings, and non-residually finite groups, Ph.D. thesis, Princeton University (1996), 71 pp.Google Scholar