Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de la Peña, Victor
and
Lai, T
2000.
Probability and Statistical Models with Applications.
de la Peña, Victor H.
and
Zamfirescu, Ingrid-Mona
2002.
Decoupling and domination inequalities with application to Wald's identity for martingales.
Statistics & Probability Letters,
Vol. 57,
Issue. 2,
p.
157.
2003.
Vol. 2,
Issue. ,
p.
1131.
Cox, Sonja
and
Veraar, Mark
2011.
Vector-valued decoupling and the Burkholder–Davis–Gundy inequality.
Illinois Journal of Mathematics,
Vol. 55,
Issue. 1,
Lindemulder, Nick
Veraar, Mark
and
Yaroslavtsev, Ivan
2019.
Positivity and Noncommutative Analysis.
p.
349.
Astashkin, S. V.
2021.
Sequences of Independent Functions in Rearrangement Invariant Spaces.
Siberian Mathematical Journal,
Vol. 62,
Issue. 2,
p.
189.
Randrianantoanina, Narcisse
2022.
Interpolation between noncommutative martingale Hardy and BMO spaces: the case.
Canadian Journal of Mathematics,
Vol. 74,
Issue. 6,
p.
1700.
Jiao, Yong
Wu, Lian
and
Zhou, Dejian
2023.
Noncommutative martingale Hardy-Orlicz spaces: Dualities and inequalities.
Science China Mathematics,
Vol. 66,
Issue. 9,
p.
2081.

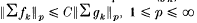 where the number
where the number 