No CrossRef data available.
Ω theorems for the complex divisor function
Published online by Cambridge University Press: 24 October 2008
Extract
This paper is a sequel to [6] and concerns the complex divisor function
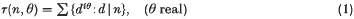
which has had a number of applications in the analytic theory of numbers. Thus Hooley's Δ-function [8] defined by
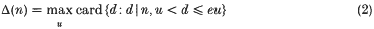
satisfies the inequality

and Erdös' τ+-function, defined by

satisfies
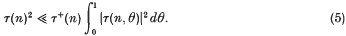
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 145 - 157
- Copyright
- Copyright © Cambridge Philosophical Society 1994
References
REFERENCES
[1]Bastick, L.. A better lower bound for Σn ≤ xτ+(n). M.Phil thesis (University of York, 1992).Google Scholar
[2]Erdös, P. and Hall, R. R.. The propinquity of divisors. B. London Math. Soc. 11 (1979), 304–307.CrossRefGoogle Scholar
[3]Halberstam, H. and Richert, H.-E.. On a result of R. R. Hall. J. Number Theory, 11 (1979), 76–89.CrossRefGoogle Scholar
[4]Hall, R. R.. Sums of imaginary powers of the divisors of integers. J. London Math. Soc. 9 (1975), 571–580.CrossRefGoogle Scholar
[5]Hall, R. R.. The propinquity of divisors. Acta Arithmetica 49 (1987), 155–163.CrossRefGoogle Scholar
[6]Hall, R. R.. Uniform upper bounds for the complex divisor function. Math. Proc. Cambridge Phil. Soc. 108 (1990), 421–427.CrossRefGoogle Scholar
[7]Hall, R. R. and Tenenbaum, G.. Divisors. Cambridge Tracts in Mathematics No. 90 (Cambridge University Press, 1988).CrossRefGoogle Scholar
[8]Hooley, C.. On a new technique and its applications to the theory of numbers. Proc. London Math. Soc. 38 (1979), 115–151.CrossRefGoogle Scholar
[9]Maier, H. and Tenenbaum, G.. On the set of divisors of an integer. Inventiones Math. 76 (1984), 121–128.CrossRefGoogle Scholar
[10]Tenenbaum, G.. Sur la concentration moyenne des diviseurs. Comment. Math. Helvetici 60 (1985), 411–428.CrossRefGoogle Scholar

