Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jackowski, Stefan
McClure, James E.
and
Oliver, Bob
1990.
Self-maps of classifying spaces of compact simple Lie groups.
Bulletin of the American Mathematical Society,
Vol. 22,
Issue. 1,
p.
65.
Ishiguro, Kenshi
1992.
Algebraic Topology Homotopy and Group Cohomology.
Vol. 1509,
Issue. ,
p.
210.
McGibbon, C.A.
and
Moller, J.M.
1992.
On spaces with the same n-type for all n.
Topology,
Vol. 31,
Issue. 1,
p.
177.
Notbohm, Dietrich
1993.
Maps between classifying spaces and applications.
Journal of Pure and Applied Algebra,
Vol. 89,
Issue. 3,
p.
273.
Ishiguro, Kenshi
and
Notbohm, Dietrich
1994.
Fibrations of classifying spaces.
Transactions of the American Mathematical Society,
Vol. 343,
Issue. 1,
p.
391.
Jackowski, Stefan
McClure, James
and
Oliver, Bob
1994.
Algebraic Topology and Its Applications.
Vol. 27,
Issue. ,
p.
81.
Aguadé, Jaume
and
Ruiz, Albert
2003.
Maps between classifying spaces of Kac–Moody groups.
Advances in Mathematics,
Vol. 178,
Issue. 1,
p.
66.
Lin, Xian Zu
2011.
Geometric realization of Adams maps.
Acta Mathematica Sinica, English Series,
Vol. 27,
Issue. 5,
p.
863.
Hornbostel, Jens
and
Schröer, Stefan
2015.
Infinite CW-complexes, Brauer groups and phantom cohomology.
Israel Journal of Mathematics,
Vol. 207,
Issue. 1,
p.
77.

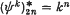 . Id
. Id