Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T17:55:27.557Z Has data issue: false hasContentIssue false
  • English
  • Français

An application of the Thue–Siegel–Roth theorem to elliptic functions

Published online by Cambridge University Press:  24 October 2008

J. Coates
J. Coates
Affiliation:
Harvard University
Get access Rights & Permissions [Opens in a new window]

Extract

Let α1, …, αn be n ≥ 2 algebraic numbers such that log α1,…, log αn and 2πi are linearly independent over the field of rational numbers Q. It is well known (see (6), Ch. 1) that the Thue–Siegel–Roth theorem implies that, for each positive number δ, there are only finitely many integers b1,…, bn satisfying

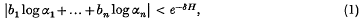
where H denotes the maximum of the absolute values of b1, …, bn. However, such an argument cannot provide an explicit upper bound for the solutions of (1), because of the non-effective nature of the theorem of Thue–Siegel–Roth. An effective proof that (1) has only a finite number of solutions was given by Gelfond (6) in the case n = 2, and by Baker(1) for arbitrary n. The work of both these authors is based on arguments from the theory of transcendental numbers. Baker's effective proof of (1) has important applications to other problems in number theory; in particular, it provides an algorithm for solving a wide class of diophantine equations in two variables (2).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 1 , January 1971 , pp. 157 - 161
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, A.Linear forms in the logarithms of algebraic numbers. Mathematika 13 (1966), 204–16.Google Scholar
(2)Baker, A.Contributions to the theory of Diophantine equations I, II. Philos. Trans. Roy. Soc. London Ser. A 263 (1968), 173–208.Google Scholar
(3)Baker, A. Paper to appear in the proceedings of a conference on Number Theory, held in Rome, December, 1968.Google Scholar
(4)Baker, A. and Coates, J.Integer points on curves of genus 1. Proc. Cambridge Philos. Soc. 67 (1970), 597–602.Google Scholar
(5)Fricke, R.Die elliptischen Funktionen und ihre Anwendungen, vol. II (Leipzig, 1916).Google Scholar
(6)Gelfond, A.Transcendental and algebraic numbers (New York, 1960).Google Scholar
(7)Leveque, W.Topics in number theory, vol. II (Reading, Mass., 1956).Google Scholar
(8)Feldman, N. I.An elliptic analogue of an inequality of A. O. Gelfond. Trans. Moscow Math. Soc. 18 (1968), 71–84.Google Scholar
(9)Siegel, C.Approximation algebraischer Zahlen. Math. Z. 10 (1921), 173–213CrossRefGoogle Scholar
Siegel, C.Approximation algebraischer Zahlen. Ges. Ab. I, 6–46.Google Scholar
(10)Siegel, C.Uber einige Anwendungen diophantischer Approximationen. Abh. Preuss. Akad. Wiss. 1 (1929).Google Scholar
Siegel, C.Uber einige Anwendungen diophantischer Approximationen. Ges. Ab. I, 209–66.Google Scholar