Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rowlands, K.
1976.
On a class of generalized functions.
Glasgow Mathematical Journal,
Vol. 17,
Issue. 1,
p.
37.

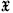 be the complex vector space consisting of all complex-valued functions of a non-negative real variable
be the complex vector space consisting of all complex-valued functions of a non-negative real variable 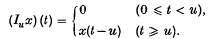
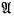 of
of 