Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T20:25:21.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Double multipliers and A*-algebras of the first kind

Published online by Cambridge University Press:  24 October 2008

M. S. Kassem  and
K. Rowlands
M. S. Kassem
Affiliation:
Department of Mathematics, Mansoura University, Egypt
K. Rowlands
Affiliation:
Department of Mathematics, University College of Wales, Aberystwyth
Get access Rights & Permissions [Opens in a new window]

Extract

Let A be an A*-algebra and let 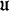denote its auxiliary norm closure. The multiplier algebras of dual A*-algebras of the first kind have been studed by Tomiuk [12], [13] and Wong[15]. In this paper we study the double multiplier algebra of A*-algebras of the first kind. In particular, we prove that, if A is an A*-algebra of the first kind, then the double multiplier algebra M(A) of A is *-isomorphic and (auxiliary norm) isometric to a subalgebra of M(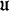), extending in the process some results established by Tomiuk[12]. We also consider the embedding of the double multiplier algebra of A in 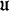**, when the latter is regarded as an algebra with the Arens product, and, in particular, we show that, for an annihilator A*-algebra, M(A) is *-isomorphic and (auxiliary norm) isometric to **.

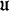Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 507 - 516
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alexander, F. E.. The bidual of A*-algebras of the first kind. J. London, Math. Soc. (2), 12 (1975), 1–6.CrossRefGoogle Scholar
[2]Barnes, B. A.. Algebras with the spectral expansion property. Illinois J. Math. 11 (1967), 284–290.CrossRefGoogle Scholar
[3]Barnes, B. A.. Subalgebras of modular annihilator algebras. Proc. Cambridge Philos. Soc. 66 (1969), 5–12.Google Scholar
[4]Busby, R. C.. Double centralizers and extensions of C*-algebras. Trans. Amer. Math. Soc. 132 (1968), 79–99.Google Scholar
[5]Davenport, J. W.. The strict dual of B*-algebras. Proc. Amer. Math. Soc. 65 (1977), 309–312.Google Scholar
[6]Kaplansky, I.. The structure of certain operator algebras. Trans. Amer. Math. Soc. 70 (1951), 219–255.CrossRefGoogle Scholar
[7]Ogasawara, T. and Yoshinaga, K.. Weakly completely continuous Banach *-algebras. Sci. Hiroshima Univ. Ser. A 18 (1954), 15–36.Google Scholar
[8]Rickart, C. E.. General Theory of Banach Algebras (Van Nostrand, 1960).Google Scholar
[9]Sentilles, F. D. and Taylor, D. C.. Factorization in Banach algebras and the general strict topology. Trans. Amer. Math. Soc. 142 (1969), 141–152.Google Scholar
[10]Taylor, D. C.. The strict topology for double centralizer algebras. Trans. Amer. Math. Soc. 150 (1970), 633–643.Google Scholar
[11]Tomiuk, B. J.. Modular annihilator A*-algebras. Canadian Math. Bull. 15 (3) (1972), 421–426.Google Scholar
[12]Tomiuk, B. J.. Multipliers on Banach algebras. Studia Math. 54 (1976), 267–283.CrossRefGoogle Scholar
[13]Tomiuk, B. J.. Multipliers on dual A*-algebras. Proc. Amer. Math. Soc. 62 (1977), 259–265.Google Scholar
[14]Wong, P. K.. On the Arens product and annihilator algebras. Proc. Amer. Math. Soc. 30 (1971), 79–83.Google Scholar
[15]Wong, P. K.. A note on isomorphisms of multiplier algebras. Canadian Math. Bull. 22 (1979), 243–245.CrossRefGoogle Scholar
[16]Yood, B.. Ideals in topological rings. Canadian J. Math. 16 (1964), 28–15.CrossRefGoogle Scholar