No CrossRef data available.
Extension of a Lemma of Stroh
Published online by Cambridge University Press: 24 October 2008
Extract
The lemma I propose to discuss may be stated as follows;
If ξ, η, ζ are three quantities whose sum is zero and λ, μ, ν three positive integers (≤n) satisfying the condition
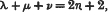
then any polynomial of order n in ξ, η, ζ can be expressed in the form
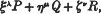
where P, Q, R are polynomials of orders n − λ, n − μ, n − ν.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 24 , Issue 2 , April 1928 , pp. 218 - 222
- Copyright
- Copyright © Cambridge Philosophical Society 1928
References
* Math. Ann. Bd XXXI, p. 444Google Scholar. Cf. Algebra of Invariants, p. 62. The case of n = 1 is trivial, exceptional, and ignored throughout.Google Scholar
† The number is: g(n−λ)+g(n−μ)+g(n−ν)+g(n−ρ)Google Scholar
* This as usual means
or
The word apolar is frequently used in the same sense.
† There is a trifling modification for two variables, the case which gives Stroh's lemma, because the principle of duality is unnecessary in one dimension. Cf. Bertini, , Geometria projettiva degli iperspazi (1923), p. 260. I return to the point in §6.Google Scholar
* Proc. Lond. Math. Soc. (2) I, pp. 345–350 (1903).Google Scholar The thesis there was to prove that expression is possible with each exponent equal to or greater than n/2 and this of course follows from the particular cases. It follows from the general theorem of §1, since one of the integers
must be divisible by 4.
* Cf. Algebra of Invariants, p. 375.Google Scholar

