Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T07:59:05.661Z Has data issue: false hasContentIssue false
  • English
  • Français

Fully admissible binary relations in topology

Published online by Cambridge University Press:  24 October 2008

D. M. G. McSherry
D. M. G. McSherry
Affiliation:
Queen's University, Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

A fully admissible binary relation (3) is an operator 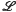, other than the equality operator 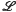and universal operator 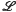, which assigns to each space |S, τ|, a reflexive, symmetric, binary relation 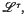, and which is such that for any continuous mapping 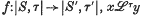implies 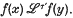. With each such relation 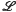, we associate a ‘separation axiom’ 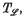, as well as ‘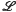-regularity’ and ‘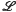-connectedness’, where 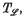≡ 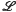-regularity + T0, and 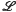-regularity + 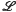-connectedness ≡ indiscreteness.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 2 , September 1977 , pp. 259 - 264
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Archangel'skii, A. V. and Wiegandt, R. Connectednesses and disconnectednesses in topology. Gen. Top. and its Appl., North-Holland Publ. Co. 5 (1975), 9–33.Google Scholar
(2)Collins, P. J.Connection properties in topological spaces. Math. Balkanics 1 (1971), 44–51.Google Scholar
(3)McSherry, D. M. G.A general theory of separation, regularity, and connectedness properties. Math. Proc. Cambridge Philos. Soc. 80 (1976), 81–90.CrossRefGoogle Scholar