Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T10:53:42.376Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on analytic functions in the unit circle

Published online by Cambridge University Press:  24 October 2008

R. E. A. C. Paley  and
A. Zygmund
R. E. A. C. Paley
Affiliation:
Trinity College
A. Zygmund
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let

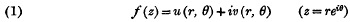
be a function regular for |z| < 1. We say that u belongs to the class Lp (p > 0) if

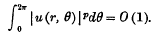
It has been proved by M. Riesz that, for p > 1, if u(r, θ) belongs to Lp, so does v (r, θ). Littlewood and later Hardy and Littlewood have shown that for 0 < p < 1 the theorem is no longer true: there exists an f(z) such that u(r, θ) belongs to every L1−ε and v(r, θ) belongs to no Lε(0 < ε < 1). The proof was based on the theorem (due to F. Riesz) that if, for an ε > 0, we have

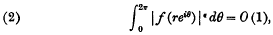
then 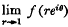f(reiθ) exists for almost every θ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 28 , Issue 3 , July 1932 , pp. 266 - 272
Copyright
Copyright © Cambridge Philosophical Society 1932

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Littlewood, J. E., “On inequalities in the theory of functions”, Proc. London Math. Soc. (2), 23 (1924), 481–519 (516–617) (no proof given)Google Scholar, Hardy, G. H. and Littlewood, J. E., “Some properties of conjugate functions”, Journal für Math., 167 (1932), 405–423 (416 ff.)Google Scholar.

* Hardy and Littlewood, loc. cit.

* Paley, R. E. A. C. and Zygmund, A., “On some series of functions, (3)”, Proc. Camb. Phil. Soc., 28 (1932), 190–205CrossRefGoogle Scholar, Lemma 19 (192).

* Zygmund, A., “On the convergence of lacunary trigonometric series”, Fundamenta Math., 16 (1930), 90–107.CrossRefGoogle Scholar