Hostname: page-component-5c6d5d7d68-lvtdw Total loading time: 0 Render date: 2024-08-11T05:24:55.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Summability by Dirichlet convolutions

Published online by Cambridge University Press:  24 October 2008

S. L. Segal
S. L. Segal
Affiliation:
University of Rochester
Get access Rights & Permissions [Opens in a new window]

Extract

Ingham (3) discusses the following summation method:

A series ∑an will be said to be summable to s if

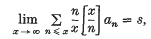
where, as usual, [x] indicates the greatest integer ≤ x. (An equivalent method was introduced somewhat earlier by Wintner (8), but the notation (I) for the above method and the attachment to Ingham's name seem to have become usual following [(1), Appendix IV].) The method (I) is intimately connected with the prime number theorem and the fact that the Riemann zeta-function ζ(s) has no zeros on the line σ = 1. Ingham proved, among other results, that (I) is not comparable with convergence but, nevertheless, for every δ > 0, (I) ⇒ (C, δ) and for every δ, 0 < δ < 1, (C, −δ) ⇒ (I), where the (C, k) are Cesàro means of order k.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 2 , April 1967 , pp. 393 - 400
Copyright
Copyright © Cambridge Philosophical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hardy, G. H.Divergent series (Oxford, 1949).Google Scholar
(2)Hardy, G. H. and Riesz, M.The general theory of dirichlet series. Cambridge Tracts in Mathematics No. 18 (Cambridge, 1915).Google Scholar
(3)Ingham, A. E.Some Tauberian theorems connected with the prime number theorem. J. London Math. Soc. 20 (1945), 171–180.CrossRefGoogle Scholar
(4)Landau, E.Über einige neuere Grenzwertsätze. Rend. circ. Mat. Palermo 34 (1912), 121–131.CrossRefGoogle Scholar
(5)Maddox, I. J.Matrix transformations of (C, −1)-summable series. Indag. Math. 27 (1965), 129–132.CrossRefGoogle Scholar
(6)Pennington, W. B.On Ingham summability and summability by Lambert Series. Proc. Cambridge Philos. Soc. 51 (1955), 65–80.CrossRefGoogle Scholar
(7)Segal, S. L.On Ingham's summation method. Canad. J. Math. 18 (1966), 97–105.CrossRefGoogle Scholar
(8)Wintner, A.Eratosthenian averages (Baltimore, 1943).Google Scholar