Article contents
Analysis of permutation equivalence in 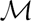 $\mathcal{M}$-adhesive transformation systems with negative application conditions
$\mathcal{M}$-adhesive transformation systems with negative application conditions
Published online by Cambridge University Press: 26 June 2014
Abstract
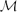 $\mathcal{M}$-adhesive categories provide an abstract framework for a large variety of specification frameworks for modelling distributed and concurrent systems. They extend the well-known frameworks of adhesive and weak adhesive HLR categories and integrate high-level constructs such as attribution as in the case of typed attributed graphs.
$\mathcal{M}$-adhesive categories provide an abstract framework for a large variety of specification frameworks for modelling distributed and concurrent systems. They extend the well-known frameworks of adhesive and weak adhesive HLR categories and integrate high-level constructs such as attribution as in the case of typed attributed graphs.
In the current paper, we investigate 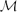 $\mathcal{M}$-adhesive transformation systems including negative application conditions (NACs) for transformation rules, which are often used in applications. For such systems, we propose an original equivalence on transformation sequences, called permutation equivalence, that is coarser than the classical switch equivalence. We also present a general construction of deterministic processes for
$\mathcal{M}$-adhesive transformation systems including negative application conditions (NACs) for transformation rules, which are often used in applications. For such systems, we propose an original equivalence on transformation sequences, called permutation equivalence, that is coarser than the classical switch equivalence. We also present a general construction of deterministic processes for 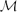 $\mathcal{M}$-adhesive transformation systems based on subobject transformation systems. As a main result, we show that the process obtained from a transformation sequence identifies its equivalence class of permutation-equivalent transformation sequences. Moreover, we show how the analysis of this process can be reduced to the analysis of the reachability graph of a generated Place/Transition Petri net. This net encodes the dependencies between rule applications of the transformation sequence, including the inhibiting effects of the NACs.
$\mathcal{M}$-adhesive transformation systems based on subobject transformation systems. As a main result, we show that the process obtained from a transformation sequence identifies its equivalence class of permutation-equivalent transformation sequences. Moreover, we show how the analysis of this process can be reduced to the analysis of the reachability graph of a generated Place/Transition Petri net. This net encodes the dependencies between rule applications of the transformation sequence, including the inhibiting effects of the NACs.
Information
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 24 , Issue 4: Structure Transformation , August 2014 , 240409
- Copyright
- Copyright © Cambridge University Press 2014
References
- 5
- Cited by

