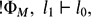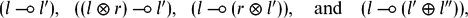There has been an increased interest in the decision problems for linear logic and its fragments. Here, we give a fully self-contained, easy-to-follow, but fully detailed, direct and constructive proof of the undecidability of a very simple Horn-like fragment of linear logic, which is accessible to a wide range of people. Namely, we show that there is a direct correspondence between terminated computations of a Minsky machine M and cut-free linear logic derivations for a Horn-like sequent of the form

\begin{equation*} \bang{\Phi_M},\ l_1 \vdash l_0, \end{equation*}

\begin{equation*} (l \llto l'),\ \ ((l\otimes r) \llto l'),\ \ (l\llto (r\otimes l')),\ \ and \ \ (l\llto (l'\oplus l'')), \end{equation*}

Neither negation, nor &, nor constants, nor embedded implications/bangs are used here.

Furthermore, our particular correspondence constructed above provides decidability for each of the Horn-like fragments whenever we confine ourselves to any two forms of the above Horn-like implications, along with the complexity bounds that come from the proof.

A ‘hybridization’ of a logic, referred to as the base logic, consists of developing the characteristic features of hybrid logic on top of the respective base logic, both at the level of syntax (i.e. modalities, nominals, etc.) and of the semantics (i.e. possible worlds). By ‘hybridized institutions’ we mean the result of this process when logics are treated abstractly as institutions (in the sense of the institution theory of Goguen and Burstall). This work develops encodings of hybridized institutions into (many-sorted) first-order logic (abbreviated $\mathcal{FOL}$) as a ‘hybridization’ process of abstract encodings of institutions into $\mathcal{FOL}$, which may be seen as an abstraction of the well-known standard translation of modal logic into $\mathcal{FOL}$. The concept of encoding employed by our work is that of comorphism from institution theory, which is a rather comprehensive concept of encoding as it features encodings both of the syntax and of the semantics of logics/institutions. Moreover, we consider the so-called theoroidal version of comorphisms that encode signatures to theories, a feature that accommodates a wide range of concrete applications. Our theory is also general enough to accommodate various constraints on the possible worlds semantics as well a wide variety of quantifications. We also provide pragmatic sufficient conditions for the conservativity of the encodings to be preserved through the hybridization process, which provides the possibility to shift a formal verification process from the hybridized institution to $\mathcal{FOL}$.

In this paper, it is proved that Girard's proof nets for multiplicative linear logic characterize free semi-star-autonomous categories.

Linearity is a multi-faceted and ubiquitous notion in the analysis and development of programming language concepts. We study linearity in a denotational perspective by picking out programs that correspond to linear functions between domains.

We propose a PCF-like language imposing linear constraints on the use of variable to program only linear functions. To entail a full abstraction result, we introduce some higher-order operators related to exception handling and parallel evaluation. We study several notions of operational equivalence and show them to coincide with our language. Finally, we present a new operational evaluation of the language that provides the base for a real implementation. It exploits the denotational linearity to provide an efficient evaluation semantics SECD-like, that avoids the use of closures.

We show that the proof-theoretic notion of logical preorder coincides with the process-theoretic notion of barbed preorder for a CCS-like process calculus obtained from the formula-as-process interpretation of a fragment of linear logic. The argument makes use of other standard notions in process algebra, namely simulation and labelled transition systems. This result establishes a connection between an approach to reason about process specifications, the barbed preorder, and a method to reason about logic specifications, the logical preorder.