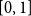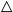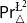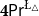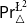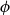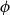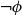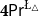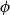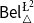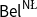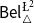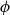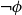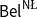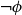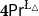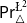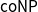We provide a fine classification of bisimilarities between states of possibly different labelled Markov processes (LMP). We show that a bisimilarity relation proposed by Panangaden that uses direct sums coincides with “event bisimilarity” from his joint work with Danos, Desharnais, and Laviolette. We also extend Giorgio Bacci’s notions of bisimilarity between two different processes to the case of nondeterministic LMP and generalize the game characterization of state bisimilarity by Clerc et al. for the latter.

We revisit the communication primitive in ambient calculi. Previously, such communication was confined to first-order (FO) mode (e.g., merely names or capabilities of ambients can be sent), local mode (e.g., the communication only occurs inside an ambient), or particular cross-hierarchy mode (e.g., parent-child communication). In this work, we explore further higher-order (HO) communication in ambient calculi. Specifically, such a communication mechanism allows sending a whole piece of a program across the borders of ambients and is the only form of communication that can happen exactly between ambients. Since ambients are basically of HO nature (i.e., those being moved may be ambients themselves), in a sense, it appears more natural to have HO communication than FO communication. We stipulate that communications merely occur between equally positioned ambients in a peer-to-peer fashion (e.g., between sibling ambients). Following this line, we drop the local or other forms of communication that violate this criterion. As the workbench, we work on a variant of Fair Ambients extended with HO communication, FAHO. This variant also strengthens the original version in that entirely real-identity interaction is guaranteed. We study the semantics, bisimulation, and expressiveness of FAHO. Particularly, we provide the operational semantics using a labeled transition system. Over the semantics, we define the bisimulation in line with the standard notion of bisimulation for ambients and prove that the bisimulation equivalence (i.e., bisimilarity) is a congruence. In addition, we demonstrate that bisimilarity coincides with observational congruence (i.e., barbed congruence). Moreover, we show that FAHO can encode a minimal Turing-complete HO calculus and thus is computationally complete.

This paper is an extended version of Bílková et al. ((2023b). Logic, Language, Information, and Computation. WoLLIC 2023, Lecture Notes in Computer Science, vol. 13923, Cham, Springer Nature Switzerland, 101–117.). We discuss two-layered logics formalising reasoning with probabilities and belief functions that combine the Łukasiewicz 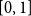[0,1]$[0,1]$-valued logic with Baaz 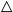\triangle$\triangle$ operator and the Belnap–Dunn logic. We consider two probabilistic logics – 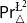\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$ (introduced by Bílková et al. 2023d. Annals of Pure and Applied Logic, 103338.) and 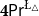\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$ (from Bílková et al. 2023b. Logic, Language, Information, and Computation. WoLLIC 2023, Lecture Notes in Computer Science, vol. 13923, Cham, Springer Nature Switzerland, 101–117.) – that present two perspectives on the probabilities in the Belnap–Dunn logic. In 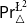\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$, every event 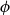\phi$\phi$ has independent positive and negative measures that denote the likelihoods of 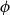\phi$\phi$ and 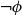\neg \phi$\neg \phi$, respectively. In 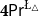\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$, the measures of the events are treated as partitions of the sample into four exhaustive and mutually exclusive parts corresponding to pure belief, pure disbelief, conflict and uncertainty of an agent in 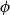\phi$\phi$. In addition to that, we discuss two logics for the paraconsistent reasoning with belief and plausibility functions from Bílková et al. ((2023d). Annals of Pure and Applied Logic, 103338.) – 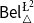\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$ and 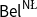\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$. Both these logics equip events with two measures (positive and negative) with their main difference being that in 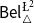\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$, the negative measure of 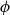\phi$\phi$ is defined as the belief in 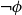\neg \phi$\neg \phi$ while in 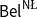\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$, it is treated independently as the plausibility of 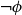\neg \phi$\neg \phi$. We provide a sound and complete Hilbert-style axiomatisation of 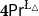\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$ and establish faithful translations between it and 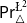\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$. We also show that the validity problem in all the logics is 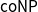\mathsf {coNP}$\mathsf {coNP}$-complete.

In this paper, by means of upper approximation operators in rough set theory, we study representations for sL-domains and its special subclasses. We introduce the concepts of sL-approximation spaces, L-approximation spaces, and bc-approximation spaces, which are special types of CF-approximation spaces. We prove that the collection of CF-closed sets in an sL-approximation space (resp., an L-approximation space, a bc-approximation space) ordered by set-theoretic inclusion is an sL-domain (resp., an L-domain, a bc-domain); conversely, every sL-domain (resp., L-domain, bc-domain) is order-isomorphic to the collection of CF-closed sets of an sL-approximation space (resp., an L-approximation space, a bc-approximation space). Consequently, we establish an equivalence between the category of sL-domains (resp., L-domains) with Scott continuous mappings and that of sL-approximation spaces (resp., L-approximation spaces) with CF-approximable relations.

A categorical axiomatic theory of creation/annihilation operators on symmetric Fock space is introduced, and the combinatorial model that motivated it is presented. Commutation relations and coherent states are considered in both frameworks.

A topological space has a domain model if it is homeomorphic to the maximal point space \mbox{Max}(P)$\mbox{Max}(P)$ of a domain P$P$. Lawson proved that every Polish space X$X$ has an \omega$\omega$-domain model P$P$ and for such a model P$P$, \mbox{Max}(P)$\mbox{Max}(P)$ is a G_{\delta }$G_{\delta }$-set of the Scott space of P$P$. Martin (2003) then asked whether it is true that for every \omega$\omega$-domain Q$Q$, \mbox{Max}(Q)$\mbox{Max}(Q)$ is G_{\delta }$G_{\delta }$-set of the Scott space of Q$Q$. In this paper, we give a negative answer to Martin’s long-standing open problem by constructing a counterexample. The counterexample here actually shows that the answer is no even for \omega$\omega$-algebraic domains. In addition, we also construct an \omega$\omega$-ideal domain \widetilde{Q}$\widetilde{Q}$ for the constructed Q$Q$ such that their maximal point spaces are homeomorphic. Therefore, \textrm{Max}(Q)$\textrm{Max}(Q)$ is a G_\delta$G_\delta$-set of the Scott space of the new model \widetilde{Q}$\widetilde{Q}$ .

We present an axiom system for what we call Prior’s Ideal Language and prove its completeness and pure completeness with respect to general models. With this is done, we explain, with examples, why this system provides a useful setting for exploring Arthur Prior’s work.

We show that the principal types of the closed terms of the affine fragment of λ-calculus, with respect to a simple type discipline, are structurally isomorphic to their interpretations, as partial involutions, in a natural Geometry of Interaction model à la Abramsky. This permits to explain in elementary terms the somewhat awkward notion of linear application arising in Geometry of Interaction, simply as the resolution between principal types using an alternate unification algorithm. As a consequence, we provide an answer, for the purely affine fragment, to the open problem raised by Abramsky of characterizing those partial involutions which are denotations of combinatory terms.

We extend the recently introduced setting of coherent differentiation by taking into account not only differentiation but also Taylor expansion in categories which are not necessarily (left) additive. The main idea consists in extending summability into an infinitary functor which intuitively maps any object to the object of its countable summable families. This functor is endowed with a canonical structure of a bimonad. In a linear logical categorical setting, Taylor expansion is then axiomatized as a distributive law between this summability functor and the resource comonad (aka. exponential). This distributive law allows to extend the summability functor into a bimonad on the coKleisli category of the resource comonad: this extended functor computes the Taylor expansion of the (nonlinear) morphisms of the coKleisli category. We also show how this categorical axiomatization of Taylor expansion can be generalized to arbitrary cartesian categories, leading to a general theory of Taylor expansion formally similar to that of cartesian differential categories, although it does not require the underlying cartesian category to be left additive. We provide several examples of concrete categories that arise in denotational semantics and feature such analytic structures.

We investigate causal computations, which take sequences of inputs to sequences of outputs such that the n$n$th output depends on the first n$n$ inputs only. We model these in category theory via a construction taking a Cartesian category \mathbb{C}$\mathbb{C}$ to another category \mathrm{St}(\mathbb{C})$\mathrm{St}(\mathbb{C})$ with a novel trace-like operation called “delayed trace,” which misses yanking and dinaturality axioms of the usual trace. The delayed trace operation provides a feedback mechanism in \mathrm{St}(\mathbb{C})$\mathrm{St}(\mathbb{C})$ with an implicit guardedness guarantee. When \mathbb{C}$\mathbb{C}$ is equipped with a Cartesian differential operator, we construct a differential operator for \mathrm{St}(\mathbb{C})$\mathrm{St}(\mathbb{C})$ using an abstract version of backpropagation through time (BPTT), a technique from machine learning based on unrolling of functions. This obtains a swath of properties for BPTT, including a chain rule and Schwartz theorem. Our differential operator is also able to compute the derivative of a stateful network without requiring the network to be unrolled.