Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vaughan, R. C.
and
Wooley, T. D.
1995.
On a certain nonary cubic form and related equations.
Duke Mathematical Journal,
Vol. 80,
Issue. 3,
Greaves, George
1997.
Some Diophantine equations with almost all solutions trivial.
Mathematika,
Vol. 44,
Issue. 1,
p.
14.
Vaughan, R. C.
1998.
Hardy's legacy to number theory.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 65,
Issue. 2,
p.
238.
Wooley, Trevor D.
2001.
Rational Points on Algebraic Varieties.
Vol. 199,
Issue. ,
p.
405.
Kawada, Koichi
and
Wooley, Trevor D.
2010.
DAVENPORT'S METHOD AND SLIM EXCEPTIONAL SETS: THE ASYMPTOTIC FORMULAE IN WARING'S PROBLEM.
Mathematika,
Vol. 56,
Issue. 2,
p.
305.
Brüdern, Jörg
and
Kawada, Koichi
2011.
The asymptotic formula in Waring’s problem for one square and seventeen fifth powers.
Monatshefte für Mathematik,
Vol. 162,
Issue. 4,
p.
385.
Wooley, Trevor D.
2012.
The Asymptotic Formula in Waring’s Problem.
International Mathematics Research Notices,
Vol. 2012,
Issue. 7,
p.
1485.
Boklan, Kent D.
and
Wooley, Trevor D.
2012.
On Weyl sums for smaller exponents.
Functiones et Approximatio Commentarii Mathematici,
Vol. 46,
Issue. 1,
Parsell, Scott T.
2012.
HUA‐TYPE ITERATION FOR MULTIDIMENSIONAL WEYL SUMS.
Mathematika,
Vol. 58,
Issue. 2,
p.
209.
Wooley, Trevor
2012.
Vinogradov's mean value theorem via efficient congruencing.
Annals of Mathematics,
Vol. 175,
Issue. 3,
p.
1575.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Laporta, Maurizio
2012.
On the number of representations in the Waring-Goldbach problem with a prime variable in an arithmetic progression.
Journal de théorie des nombres de Bordeaux,
Vol. 24,
Issue. 2,
p.
355.
HARVEY, M. P.
2013.
MINOR ARC MOMENTS OF WEYL SUMS.
Glasgow Mathematical Journal,
Vol. 55,
Issue. 1,
p.
97.
Wooley, Trevor D.
2013.
Vinogradov’s mean value theorem via efficient congruencing, II.
Duke Mathematical Journal,
Vol. 162,
Issue. 4,
Parsell, Scott T.
and
Wooley, Trevor D.
2014.
Exceptional Sets for Diophantine Inequalities.
International Mathematics Research Notices,
Vol. 2014,
Issue. 14,
p.
3919.
Banks, William D.
Güloğlu, Ahmet M.
and
Vaughan, Robert C.
2015.
Waring’s problem for Beatty sequences and a local to global principle.
Journal de théorie des nombres de Bordeaux,
Vol. 26,
Issue. 1,
p.
1.
Bourgain, Jean
and
Demeter, Ciprian
2015.
The proof of the l^2 Decoupling Conjecture.
Annals of Mathematics,
p.
351.
Wooley, Trevor D.
2015.
Mean value estimates for odd cubic Weyl sums.
Bulletin of the London Mathematical Society,
p.
bdv066.
Kuo, Wentang
Liu, Yu-Ru
and
Zhao, Xiaomei
2019.
The asymptotic estimates and Hasse principle for multidimensional Waring's problem.
Advances in Mathematics,
Vol. 353,
Issue. ,
p.
1.
VAUGHAN, R. C.
2021.
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI.
Glasgow Mathematical Journal,
Vol. 63,
Issue. 1,
p.
223.


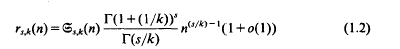
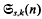 , the
, the 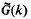 to be the smallest value of
to be the smallest value of 