Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-30T03:43:20.144Z Has data issue: false hasContentIssue false
  • English
  • Français

DYADIC SHIFT RANDOMIZATION IN CLASSICAL DISCREPANCY THEORY

Part of: Other (nonclassical) types of functional analysis Miscellaneous applications of functional analysis Combinatorial probability Extremal combinatorics

Published online by Cambridge University Press:  06 May 2015

M. M. Skriganov
M. M. Skriganov*
Affiliation:
St. Petersburg Department of Steklov Institute of Mathematics, Fontanka 27, St. Petersburg 191023, Russia email maksim88138813@mail.ru
Get access

Abstract

Dyadic shifts 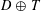$D\oplus T$ of point distributions 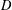$D$ in the 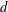$d$-dimensional unit cube 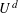$U^{d}$ are considered as a form of randomization. Explicit formulas for the 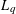$L_{q}$-discrepancies of such randomized distributions are given in the paper in terms of Rademacher functions. Relying on the statistical independence of Rademacher functions, Khinchin’s inequalities, and other related results, we obtain very sharp upper and lower bounds for the mean 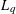$L_{q}$-discrepancies, 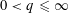$0<q\leqslant \infty$. The upper bounds imply directly a generalization of the well-known Chen theorem on mean discrepancies with respect to dyadic shifts (Theorem 2.1). From the lower bounds, it follows that for an arbitrary 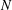$N$-point distribution 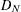$D_{N}$ and any exponent 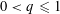$0<q\leqslant 1$, there exist dyadic shifts 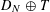$D_{N}\oplus T$ such that the 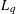$L_{q}$-discrepancy 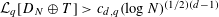${\mathcal{L}}_{q}[D_{N}\oplus T]>c_{d,q}(\log N)^{(1/2)(d-1)}$ (Theorem 2.2). The lower bounds for the 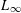$L_{\infty }$-discrepancy are also considered in the paper. It is shown that for an arbitrary 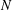$N$-point distribution 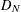$D_{N}$, there exist dyadic shifts 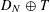$D_{N}\oplus T$ such that 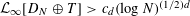${\mathcal{L}}_{\infty }[D_{N}\oplus T]>c_{d}(\log N)^{(1/2)d}$ (Theorem 2.3).

MSC classification

Primary: 05D99: None of the above, but in this section 46N99: None of the above, but in this section
Secondary: 46S99: None of the above, but in this section 60C99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 183 - 209
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beck, J. and Chen, W. W. L., Irregularities of Distribution (Cambridge Tracts in Mathematics 89), Cambridge University Press (1987).CrossRefGoogle Scholar
Bilyk, D., Roth’s orthogonal function method in discrepancy theory and some new connections. In A Panorama of Discrepancy Theory (Lecture Notes in Mathematics 2107) (eds Chen, W. W. L., Srivastav, A. and Travaglini, G.), Springer (New York, 2014), 65–149.Google Scholar
Bilyk, D. and Lacey, M. T., On the small ball inequality in three dimensions. Duke Math. J. 143 2008, 81–115.CrossRefGoogle Scholar
Bilyk, D. and Lacey, M. T., The supremum norm of the discrepancy function: recent results and connections. In Monte Carlo and Quasi-Monte Carlo Methods 2012 (Springer Proceedings in Mathematics and Statistics 65) (eds Dick, J., Kuo, F. Y., Peters, G. W. and Sloan, I. H.), Springer (New York, 2013), 23–38.CrossRefGoogle Scholar
Bilyk, D., Lacey, M. T. and Vagharshakyan, A., On the small ball inequality in all dimensions. J. Funct. Anal. 254 2008, 2470–2502.CrossRefGoogle Scholar
Chen, W. W. L., On irregularities of distribution. Mathematika 27 1980, 153–170.CrossRefGoogle Scholar
Chen, W. W. L., On irregularities of distribution II. Quart. J. Math. 34 1983, 257–279.CrossRefGoogle Scholar
Chen, W. W. L., Srivastav, A. and Travaglini, G. (Eds.), A Panorama of Discrepancy Theory (Lecture Notes in Mathematics 2107), Springer (New York, 2014).CrossRefGoogle Scholar
Chen, W. W. L. and Skriganov, M. M., Upper bounds in classical discrepancy theory. In A Panorama of Discrepancy Theory (Lecture Notes in Mathematics 2107) (eds Chen, W. W. L., Srivastav, A. and Travaglini, G.), Springer (New York, 2014), 3–64.CrossRefGoogle Scholar
Chow, Y. S. and Teicher, H., Probability Theory: Independence, Interchangeability, Martingales, 3rd edn., Springer (New York, 1997).CrossRefGoogle Scholar
Golubov, B. I., Efimov, A. V. and Skvortsov, V. A., Walsh Series and Transformations: Theory and Applications, Nauka (Moscow, 1987); Engl. transl., Mathematics and its Applications (Soviet Ser. 64), Kluwer (Dordrecht, 1991).Google Scholar
Matoušek, J., Geometric Discrepancy: An Illustrated Guide (Algorithms and Combinatorics 18), 2nd edn., Springer (New York, 2010).Google Scholar
Peshkir, G. and Shiryaev, A. N., Khinchin inequality and a martingale extention of the sphere of their action. Uspekhi Mat. Nauk 50(5) 1995, 3–62; Engl. transl., Russian Math. Surveys 50(5) (1995), 849–904.Google Scholar
Skriganov, M. M., Khinchin’s inequality and Chen’s theorem. Algebr. Anal. 23(4) 2011, 179–204; Engl. transl., St. Petersburg Math. J. 23(4) (2012), 761–778.Google Scholar
Skriganov, M. M., On mean values of the L q -discrepancies of point distributions. Algebr. Anal. 24(6) 2012, 196–225; Engl. transl., St. Petersburg Math. J. 24(6) (2013), 991–1012.Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions (Princeton Mathematical Series 30), Princeton University Press (Princeton, NJ, 1970).Google Scholar
Zygmund, A., Trigonometric Series, Vols. 1 and 2, 3rd edn., Cambridge University Press (Cambridge, 2002).Google Scholar