Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T19:14:12.661Z Has data issue: false hasContentIssue false
  • English
  • Français

ISOSPECTRALITY FOR GRAPH LAPLACIANS UNDER THE CHANGE OF COUPLING AT GRAPH VERTICES: NECESSARY AND SUFFICIENT CONDITIONS

Part of: General theory in ordinary differential equations General mathematical topics and methods in quantum theory General theory of linear operators

Published online by Cambridge University Press:  16 January 2015

Yulia Ershova ,
Irina I. Karpenko  and
Alexander V. Kiselev
Yulia Ershova
Affiliation:
Institute of Mathematics, National Academy of Sciences of Ukraine, Tereschenkivska st. 3, Kiev-4, 01601, Ukraine email julija.ershova@gmail.com
Irina I. Karpenko
Affiliation:
Department of Algebra and Functional Analysis, V.I. Vernadsky Taurida National University, 4 Vernadsky pr., Autonomous Republic of Crimea, Simferopol, 95007, Ukraine email i_karpenko@ukr.net
Alexander V. Kiselev
Affiliation:
Department of Functional Analysis, Pidstryhach Institute for Applied Problems of Mechanics and Mathematics, National Academy of Sciences of Ukraine, 3-b Naukova Str., 79060 L’viv, Ukraine Department of Higher Mathematics and Mathematical Physics, St. Petersburg State University, 1 Ulianovskaya Street, St. Petersburg, St. Peterhoff, 198504, Russia email alexander.v.kiselev@gmail.com
Get access

Abstract

Laplace operators on finite compact metric graphs are considered under the assumption that matching conditions at graph vertices are of types 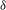${\it\delta}$ and 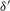${\it\delta}^{\prime }$. Assuming rational independence of edge lengths, necessary and sufficient conditions for isospectrality of two Laplacians defined on the same graph are derived and scrutinized. It is proved that the spectrum of a graph Laplacian uniquely determines matching conditions for “almost all” graphs.

MSC classification

Primary: 47A10: Spectrum, resolvent
Secondary: 34A55: Inverse problems 81Q35: Quantum mechanics on special spaces
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 210 - 242
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurova, E. N., Kandagura, A. N. and Karpenko, I. I., The criterion of simplicity for symmetric operator on a graph. Methods Funct. Anal. Topology 20(2) 2014, 117–123.Google Scholar
Avdonin, S. and Kurasov, P., Inverse problems for quantum trees. Inverse Probl. Imaging 2 2008, 1–21.CrossRefGoogle Scholar
Avdonin, S., Kurasov, P. and Nowaczyk, M., Inverse problems for quantum trees II. Recovering matching conditions for star graphs. Inverse Probl. Imaging 4/4 2010, 579–598.CrossRefGoogle Scholar
Belishev, M. I. and Vakulenko, A. F., Inverse problems on graphs: recovering the tree of strings by the BC-method. J. Inverse Ill-Posed Probl. 14(1) 2006, 29–46.CrossRefGoogle Scholar
Belishev, M. I. and Wada, N., On revealing graph cycles via boundary measurements. Inverse Problems 25(10) 2009 105011, 21 pp.CrossRefGoogle Scholar
Berkolaiko, G. and Kuchment, P., Introduction to Quantum Graphs (Mathematical Surveys and Monographs 186), American Mathematical Society (Providence, RI, 2012).CrossRefGoogle Scholar
Cassels, J. W. S., An Introduction to Diophantine Approximation (Cambridge Tracts in Mathematics and Mathematical Physics 45), Cambridge University Press (New York, 1957).Google Scholar
Carlson, R., Inverse eigenvalue problems on directed graphs. Trans. Amer. Math. Soc. 351(10) 1999, 4069–4088.CrossRefGoogle Scholar
Derkach, V. A. and Malamud, M. M., Generalized resolvents and the boundary value problems for Hermitian operators with gaps. J. Funct. Anal. 95 1991, 1–95.CrossRefGoogle Scholar
Ershova, Yu., Karpenko, I. I. and Kiselev, A. V., Isospectrality for graph Laplacians under the change of coupling at graph vertices. J. Spectral Theory (to appear), arXiv:1405.2997 [math.sp].Google Scholar
Ershova, Yu. and Kiselev, A. V., Trace formulae for graph Laplacians with applications to recovering matching conditions. Methods Funct. Anal. Topology 18(4) 2012, 343–359.Google Scholar
Ershova, Yu. and Kiselev, A. V., Trace formulae for Schrodinger operators on metric graphs with applications to recovering matching conditions. Methods Funct. Anal. Topology 20(2) 2014, 134–148.Google Scholar
Exner, P., Lattice Kronig–Penney models. Phys. Rev. Lett. 74 1995, 3503–3506.CrossRefGoogle ScholarPubMed
Exner, P., A duality between Schrödinger operators on graphs and certain Jacobi matrices. Ann. Inst. Henri Poincaré Phys. Theor. 66 1997, 359–371.Google Scholar
Gorbachuk, V. I. and Gorbachuk, M. L., Boundary Value Problems for Operator Differential Equations (Mathematics and its Applications (Soviet Series) 48), Kluwer (Dordrecht, 1991). Translated and revised from the 1984 Russian original.CrossRefGoogle Scholar
Gutkin, B. and Smilansky, U., Can one hear the shape of a graph? J. Phys. A 34 2001, 6061–6068.CrossRefGoogle Scholar
Kočubeĭ, A. N., On extension of symmetric operators and symmetric binary relations. Math. Notes 17 1975, 41–48.Google Scholar
Kočubeĭ, A. N., Characteristic functions of symmetric operators and their extensions. Izv. Akad. Nauk Arm. SSR Ser. Mat. 15(3) 1980, 219–232 (in Russian).Google Scholar
Kostrykin, V., Potthoff, J. and Schrader, R., Heat kernels on metric graphs and a trace formula. In Adventures in Mathematical Physics (Contemporary Mathematics 447), American Mathematical Society (Providence, RI, 2007), 175–198.CrossRefGoogle Scholar
Kostrykin, V. and Schrader, R., Kirchhoff’s rule for quantum wires. J. Phys. A 32 1999, 595–630.CrossRefGoogle Scholar
Kottos, T. and Smilansky, U., Periodic orbit theory and spectral statistics for quantum graphs. Ann. Phys. 274 1999, 76–124.CrossRefGoogle Scholar
Kuchment, P., Quantum graphs: an introduction and a brief survey. In Analysis on Graphs and its Applications (Proceedings of Symposia in Pure Mathematics 77), American Mathematical Society (Providence, RI, 2008), 291–314.CrossRefGoogle Scholar
Kurasov, P., Graph Laplacians and topology. Ark. Mat. 46 2008, 95–111.CrossRefGoogle Scholar
Kurasov, P., Inverse problem for Aharonov–Bohm rings. Math. Proc. Cambridge Philos. Soc. 148 2010, 331–362.CrossRefGoogle Scholar
Kurasov, P., Malenová, G. and Naboko, S., Spectral gap for quantum graphs and their edge connectivity. J. Phys. A 46(27) 2013 275309, 16 pp.CrossRefGoogle Scholar
Kurasov, P. and Nowaczyk, M., Inverse spectral problem for quantum graphs. J. Phys. A: Math. Gen. 38 2005, 4901–4915. Correction: J. Phys. A: Math. Gen. 39 (2006), 993.CrossRefGoogle Scholar
Levin, B. Ya., Lectures on Entire Functions (Translations of Mathematical Monographs 150), American Mathematical Society (Providence, RI, 1996). In collaboration with and with a preface by Yu. Lyubarskii, M. Sodin and V. Tkachenko. Translated from the Russian manuscript by Tkachenko.CrossRefGoogle Scholar
Pivovarchik, V. and Taystruk, O., On characteristic functions of operators on equilateral graphs. Methods Funct. Anal. Topology 18(2) 2012, 189–197.Google Scholar
Roth, J. P., Le spectre du Laplacien sur un graphe. In Théorie du Potentiel (Orsay, 1983) (Lecture Notes in Mathematics 1096), 521–539.CrossRefGoogle Scholar
Ryzhov, V., Functional model of a class of nonselfadjoint extensions of symmetric operators. Oper. Theory Adv. Appl. 174 2007, 117–158.Google Scholar
Shabat, B. V., Introduction to Complex Analysis. Part II. Functions of Several Variables (Translations of Mathematical Monographs 110), American Mathematical Society (Providence, RI, 1992). Translated from the third (1985) Russian edition by J. S. Joel.CrossRefGoogle Scholar
Tutte, W. T., Graph Theory (Encyclopedia of Mathematics and its Applications 21), Addison-Wesley (Reading, MA, 1984). With a foreword by C. St. J. A. Nash-Williams..Google Scholar