Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T21:07:50.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure function properties of the asymmetric Cauchy process

Published online by Cambridge University Press:  26 February 2010

John Hawkes
John Hawkes
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, Michigan, U.S.A.
Get access

Extract

§1. Preliminaries. A Cauchy process in d-dimensional Euclidean space, Rd, is a stochastic process, Xt(ω), with stationary independent increments and with a continuous transition density, p(t, y − x) defined by

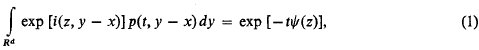
and

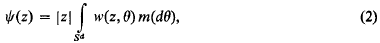
where m, the isotropic measure, is a probability measure on Sd, the unit sphere in Rd, such that when d > 1 the support of m is not contained in any d − 1 dimensional subspace. In (2) w is given by

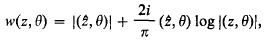
where 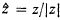. It follows that for each t > 0 and y we have p(t, y) > 0 and that for each t > 0 p(t, y) is a bounded and continuous function of y. Xt(ω) can be considered as being a standard Markov process (for a full description of the definition of such a process see Chapter 1 of [1]) and in particular we can assume that the sample functions of Xt(ω) are right continuous and have left limits. We can also assume that Xt(ω) enjoys the strong Markov property. We write Px and Ex for probabilities and expectations conditional on X0(ω) = x, and we write P for P0.

Type
Research Article
Information
Mathematika , Volume 17 , Issue 1 , June 1970 , pp. 68 - 78
Copyright
Copyright © University College London 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Blumenthal, R. M. and Getoor, R. K., Markov processes and potential theory (Academic Press, New York, 1968).Google Scholar
2.Blumenthal, R. M., Getoor, R. K., “Sample functions of stochastic processes with stationary independent increments”, Math. Mech., 10 (1961), 493–516.Google Scholar
3.Blumenthal, R. M., Getoor, R. K., “The dimension of the set of zeros and the graph of a symmetric stable process”, Illinois J. Math., 6 (1962), 308–316.CrossRefGoogle Scholar
4.Blumenthal, R. M., Getoor, R. K., “Local times and Markov processes”, Z. Wahrscheinlichkeitstheorie, 3 (1964), 50–74.CrossRefGoogle Scholar
5.Kingman, J. F. C., “Recurrence properties of processes with stationary independent increments”, J. Australian Math. Soc, 4 (1964), 223–228.CrossRefGoogle Scholar
6.Marstrand, J. M., “The dimension of cartesian product sets”, Proc. Camb. Phil. Soc, 50 (1954), 198–202.CrossRefGoogle Scholar
7.Orey, S., “Polar sets for processes with stationary independent increments”, Proceedings of the Madison Conference on Markov processes and potential theory (John Wiley, New York 1967), 117–126.Google Scholar
8.Port, S. C. and Stone, C., “The asymmetric Cauchy processes on the line”, Ann. Math. Stat., 40 (1969), 137–143.CrossRefGoogle Scholar
9.Pruitt, W. E. and Taylor, S. J., “Sample path properties of processes with stable components”, Z. Wahrscheinlichkeitstheorie, 12 (1969), 267–289.CrossRefGoogle Scholar
10.Taylor, S. J., “Sample path properties of a transient stable process”, J. Math. Mech., 16 (1967), 1229–1246.Google Scholar
11.Taylor, S. J. and Wendel, J. G., “The exact Hausdorff measure of the zero set of a stable process”, Z. Wahrscheinlichkeitstheorie, 6 (1966), 170–180.CrossRefGoogle Scholar