Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goodman, Jacob E.
and
Pollack, Richard
1986.
There are asymptotically far fewer polytopes than we thought.
Bulletin of the American Mathematical Society,
Vol. 14,
Issue. 1,
p.
127.
Kalai, Gil
1988.
Many triangulated spheres.
Discrete & Computational Geometry,
Vol. 3,
Issue. 1,
p.
1.
GOODMAN, JACOB E.
and
POLLACK, RICHARD
1989.
New Bounds on Higher Dimensional Configurations and Polytopesa.
Annals of the New York Academy of Sciences,
Vol. 555,
Issue. 1,
p.
205.
YAO, F. Frances
1990.
Algorithms and Complexity.
p.
343.
Alon, Noga
1990.
Ramsey graphs cannot be defined by real polynomials.
Journal of Graph Theory,
Vol. 14,
Issue. 6,
p.
651.
Alon, Noga
Katchalski, Meir
and
Scheinerman, Edward R.
1990.
Not All Graphs are Segment T-graphs.
European Journal of Combinatorics,
Vol. 11,
Issue. 1,
p.
7.
Goodman, Jacob E.
and
Pollack, Richard
1991.
The complexity of point configurations.
Discrete Applied Mathematics,
Vol. 31,
Issue. 2,
p.
167.
Richter, Jürgen
and
Sturmfels, Bernd
1991.
On the topology and geometric construction of oriented matroids and convex polytopes.
Transactions of the American Mathematical Society,
Vol. 325,
Issue. 1,
p.
389.
Croft, Hallard T.
Falconer, Kenneth J.
and
Guy, Richard K.
1991.
Unsolved Problems in Geometry.
Vol. 2,
Issue. ,
p.
48.
BAYER, Margaret M.
and
LEE, Carl W.
1993.
Handbook of Convex Geometry.
p.
485.
BOKOWSKI, J.
1993.
Handbook of Convex Geometry.
p.
555.
ECKHOFF, Jürgen
1993.
Handbook of Convex Geometry.
p.
389.
Goodman, Jacob E.
and
Pollack, Richard
1993.
New Trends in Discrete and Computational Geometry.
Vol. 10,
Issue. ,
p.
103.
Thomas, F.
and
Torras, C.
1994.
Interference detection between non-convex polyhedra revisited with a practical aim.
p.
587.
Alt, Helmut
Godau, Michael
and
Whitesides, Sue
1996.
Graph Drawing.
Vol. 1027,
Issue. ,
p.
8.
Kung, Joseph P.S.
1996.
Vol. 1,
Issue. ,
p.
157.
Roy, Marie-Françoise
2000.
Development of Mathematics, 1950–2000.
p.
939.
Spencer, Joel
and
Tóth, Géza
2002.
Crossing numbers of random graphs.
Random Structures & Algorithms,
Vol. 21,
Issue. 3-4,
p.
347.
Roy, Marie-Françoise
2003.
Discrete and Computational Geometry.
Vol. 25,
Issue. ,
p.
737.
2005.
Research Problems in Discrete Geometry.
p.
325.

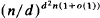 , as
, as 