Hostname: page-component-77f85d65b8-pkds5 Total loading time: 0 Render date: 2026-04-19T20:27:10.156Z Has data issue: false hasContentIssue false
  • English
  • Français

On surface Bieberbach groups

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  26 February 2010

F. E. A. Johnson
F. E. A. Johnson
Affiliation:
Department of Mathematics, University College London, Gower Street, London. WCIE 6BT.
Get access

Extract

Recall that a Poincaré Duality group G is said to be smoothly realisable when there exists a smooth closed manifold XG of homotopy type K(G, 1). In this note we prove

Theorem 1. Let

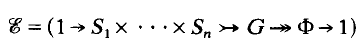
be an exact sequence of groups in which each Si is a Surface group, with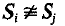for i ≠ j, Ф is finite and G is torsion free. Then the Poincaré Duality group G is smoothly realisable.

MSC classification

Secondary: 20F34: Fundamental groups and their automorphisms

Information

Type
Research Article
Information
Mathematika , Volume 34 , Issue 1 , June 1987 , pp. 82 - 85
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Bieberbach, L.. Über die Bewegungsgruppen der Euklidischen Räume I. Math. Ann., 70 (1911), 297–336.CrossRefGoogle Scholar
2.Johnson, F. E. A.. Automorphisms of direct products of groups and their geometric realisations. Math. Ann., 263 (1983), 343–364.CrossRefGoogle Scholar
3.Johnson, F. E. A.. On the generalised Bieberbach-Nielsen problem. In preparation.Google Scholar
4.Johnson, F. E. A. and Wall, C. T. C.. On groups satisfying Poincare Duality. Ann. of Math., 96 (1972), 592–598.CrossRefGoogle Scholar
5.Kerckhofi, S. P.. The Nielsen realisation problem. Ann. of Math., 117 (1983), 235–265.Google Scholar
6.Neumann, H.. Varieties of groups. Ergebnisse der Mathematik no. 37 (Berlin, Springer, 1966).Google Scholar