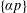Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rudnick, Zeév
2018.
A METRIC THEORY OF MINIMAL GAPS.
Mathematika,
Vol. 64,
Issue. 3,
p.
628.
Bloom, Thomas F.
Chow, Sam
Gafni, Ayla
and
Walker, Aled
2018.
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY.
Mathematika,
Vol. 64,
Issue. 3,
p.
679.
Hinrichs, Aicke
Kaltenböck, Lisa
Larcher, Gerhard
Stockinger, Wolfgang
and
Ullrich, Mario
2019.
On a multi-dimensional Poissonian pair correlation concept and uniform distribution.
Monatshefte für Mathematik,
Vol. 190,
Issue. 2,
p.
333.
Aistleitner, Christoph
Lachmann, Thomas
and
Technau, Niclas
2019.
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS.
Mathematika,
Vol. 65,
Issue. 4,
p.
929.
Lachmann, Thomas
and
Technau, Niclas
2019.
On exceptional sets in the metric Poissonian pair correlations problem.
Monatshefte für Mathematik,
Vol. 189,
Issue. 1,
p.
137.
Rudnick, Zeév
and
Technau, Niclas
2020.
The metric theory of the pair correlation function of real-valued lacunary sequences.
Illinois Journal of Mathematics,
Vol. 64,
Issue. 4,
Marklof, Jens
2020.
Pair correlation and equidistribution on manifolds.
Monatshefte für Mathematik,
Vol. 191,
Issue. 2,
p.
279.
Steinerberger, Stefan
2020.
Poissonian pair correlation in higher dimensions.
Journal of Number Theory,
Vol. 208,
Issue. ,
p.
47.
Bloom, Thomas F.
and
Walker, Aled
2020.
GCD sums and sum-product estimates.
Israel Journal of Mathematics,
Vol. 235,
Issue. 1,
p.
1.
Cohen, Alex
2021.
Poissonian correlation of higher order differences.
Journal of Number Theory,
Vol. 229,
Issue. ,
p.
463.
RAMÍREZ, FELIPE A.
2022.
Remarks about inhomogeneous pair correlations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 173,
Issue. 2,
p.
369.
Hauke, Manuel
and
Zafeiropoulos, Agamemnon
2024.
Weak Poissonian correlations.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 203,
Issue. 6,
p.
2711.
Altman, Daniel
and
Chase, Zachary
2025.
On the smallest gap in a sequence with Poisson pair correlations.
Combinatorics, Probability and Computing,
Vol. 34,
Issue. 2,
p.
283.
HAUKE, MANUEL
and
ZAFEIROPOULOS, AGAMEMNON
2025.
On inhomogeneous Poissonian pair correlations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 179,
Issue. 1,
p.
17.
Babu, C.G. Karthick
Malavika, E.
and
Viswanadham, G.K.
2026.
Poissonian pair correlation of linear generalized monomials over primes.
Journal of Number Theory,
Vol. 279,
Issue. ,
p.
270.