Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T21:36:24.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Random Banach spaces: The limitations of the method

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  26 February 2010

Piotr Mankiewicz  and
Stanislaw J. Szarek
Piotr Mankiewicz
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Warsaw, Poland.
Stanislaw J. Szarek
Affiliation:
Department of Mathematics, Case Western Reserve University, 10900 Euclid Avenue, Cleveland, Ohio 44106-7058, U.S.A.
Get access

Extract

We shall study the properties of typical n-dimensional subspaces of 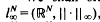, or equivalently, -typical n-dimensional quotients of 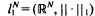, where the meaning of what is typical and what is not is defined in terms of the Haar measure μn,N on the Grassmann manifold Gn,N of all n-dimensional subspaces of .

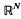MSC classification

Secondary: 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Mathematika , Volume 41 , Issue 2 , December 1994 , pp. 239 - 250
Copyright
Copyright © University College London 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ca.-P.Carl, B. and Pajor, A.. Gelfand numbers of operators with values in a Hilbert space. Invent. Math., 94 (1988), 479–504.CrossRefGoogle Scholar
Gl.1.Gluskin, E. D.. The diameter of the Minkowski compactum is roughly equal to n. Func. Anal i Priloz., 15 (1981), 72–73 (in Russian).Google Scholar
G1.2.Gluskin, E. D.. Finite dimensional analog of a space without basis. Dokl. AN SSSR, 261 (5) (1981), 1046–1050 (in Russian).Google Scholar
G1.3.Gluskin, E. D.. Oktaeder is poorly approximable by random subspaces. Func. Anal, i Priloz., 20 (1) (1986), 14–20 (in Russian).Google Scholar
G1.4.Gluskin, E. D.. Extremal properties of orthogonal parallelograms and their applications to the geometry of Banach spaces. Mat. Sbor., 136 (178) (1988), 85–96 (in Russian)Google Scholar
G1.5.Gluskin, E. D.. Personal communications.Google Scholar
F-L-M.Figiel, T., Lindenstrauss, J. and Milman, V. D.. The dimension of almost spherical sections of convex bodies. Acta Math., 139 (1977), 56–94.CrossRefGoogle Scholar
Ma.1.Mankiewicz, P.. Factoring the identity operator on a subspace of . Studia Math., 95 (1989), 134–139.CrossRefGoogle Scholar
Ma.2.Mankiewicz, P.. Subspace mixing properties of operators in with applications to Gluskin spaces. Studia Math., 88 (1988), 51–67.CrossRefGoogle Scholar
Ma.-T.Mankiewicz, P. and Tomczak-Jaegermann, N.. Random subspaces and quotients of finite dimensional Banach spaces. Preprint. Odense University (1998).Google Scholar
P-T.Pajor, A. and Tomczak-Jaegermann, N.. Subspaces of small codimensions of finite dimensional Banach spaces. Proc. AMS, 97 (1986), 637–642.CrossRefGoogle Scholar
Pi.1.Pisier, G.. Remarques sur un resultat non publie de B. Maurey. Seminaire d'Analyse Fonctionnelk, Ecole Polytechnique (1980-1981) exp. 5.Google Scholar
Pi.2.Pisier, G.. A new approach to several results of V. Milman. J. Reine Angew. Math., 393 (1989), 115–131.Google Scholar
Si.Silverstein, J.. The smallest eigenvalue of a large dimensional Wishart matrix. Ann. Probab., 13 (1985), 1364–1368.CrossRefGoogle Scholar
Sz.1.Szarek, S. J.. On finite dimensional basis problem with an appendix on nets of Grassmann manifolds. Acta. Math., 151 (1983), 153–179.CrossRefGoogle Scholar
Sz.2.Szarek, S. J.. On the existence and uniqueness of complex structure and spaces with few operators. Trans. Amer. Math. Soc., 293 (1986), 339–353.Google Scholar
Sz.3.Szarek, S. J.. Spaces with large distance to and random matrices. Amer. J. Math., 112 (1990), 899–942.CrossRefGoogle Scholar
Sz-T.Szarek, S. J. and Tomczak-Jaegermann, N.. On nearly Euclidean decomposition for some classes of Banach spaces. Comp. Math., 40 (1980), 367–385.Google Scholar
T.Tong, Y.. Probability Inequalities in Multivariate distributions. (Academic Press, New York).Google Scholar