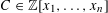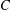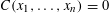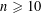Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dong, Aiju
Huang, Linzhe
and
Xue, Boqing
2018.
Operator algebras associated with multiplicative convolutions of arithmetic functions.
Science China Mathematics,
Vol. 61,
Issue. 9,
p.
1665.