Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T05:52:14.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Some extremal problems for convex bodies

Published online by Cambridge University Press:  26 February 2010

C. A. Rogers  and
G. C. Shephard
C. A. Rogers
Affiliation:
University of Birmingham, Birmingham, 15.
G. C. Shephard
Affiliation:
University of Birmingham, Birmingham, 15.
Get access

Extract

If K is a convex body in n-dimensional space, let SK denote the closed n-dimensional sphere with centre at the origin and with volume equal to that of K. If H and K are two such convex bodies let C(H, K) denote the least convex cover of the union of H and K, and let V*(H, K) denote the maximum, taken over all points x for which the intersection 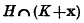is not empty, of the volume

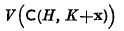
of the set 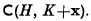. The object of this paper is to discuss some of the more interesting consequences of the following general theorem.

Type
Research Article
Information
Mathematika , Volume 5 , Issue 2 , December 1958 , pp. 93 - 102
Copyright
Copyright © University College London 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 93 note † Since the choice of a may not be unique, the symbol R*K may not denote a unique set; no confusion should arise as all the possible sets, which R*K may denote, have the same volume.

page 93 note ‡ Rogers, C. A. and Shephard, G. C., Journal London Math. Soc., 33 (1958), 270–281.CrossRefGoogle Scholar

page 95 note † Loc. cit., 210–211.

page 95 note ‡ Proc. Cambridge Phil. Soc., 47 (1951), 245–247.CrossRefGoogle Scholar

page 95 note § We define the least convex cover to be the least convex set containing the given set; it is not necessarily closed.

page 95 note ║ See, for example, Bonnesen-Fenchel, , Theorie der konvexen Körper (Ergebnisse der Math.), §11.Google Scholar

page 97 note † See, for example, Eggleston, H. G., Convexity (Cambridge 1958), 98.CrossRefGoogle Scholar

page 97 note ‡ Loc. cit., Satz 4.

page 97 note § Loc. cit., Lemma 2.

page 97 note ║ Eggleston, H. G., loc. cit., Ch. 5.Google Scholar

page 98 note † This supposition is convenient for the purely technical reason that it enables us to take the index set I introduced below to be the union of H and K.

page 100 note † Loc. cit.

page 101 note † Macbeath, A. M., Canadian J. of Math., 3 (1951), 54–61.CrossRefGoogle Scholar