Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T08:32:23.727Z Has data issue: false hasContentIssue false
  • English
  • Français

Some inequalities concerning symmetric forms

Published online by Cambridge University Press:  26 February 2010

J. N. Whiteley
J. N. Whiteley
Affiliation:
Department of Mathematics, University College, London.
Get access

Extract

Let a1, …, am and b1, … bm be non-negative real numbers. The well-known inequality of Minkowski states that

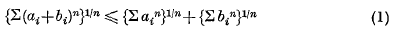
if n ≥ 1. If n is a positive integer, this inequality asserts a property of a particular symmetric form (i.e. homogeneous polynomial) in m variables, namely the sum of the n-th powers of the variables. Some time ago, Prof. A. C. Aitken conjectured that similar properties are possessed by certain other symmetric forms. In particular, let E(n)(a) denote the n-th elementary symmetric function of a1, …, am and let C(n)(a) denote the n-th complete symmetric function of a1, …, am, the formal definitions being

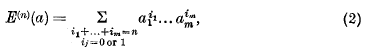
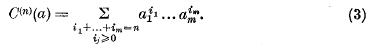
Then Prof. Aitken conjectured that

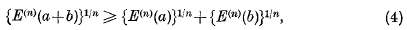
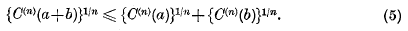
Type
Research Article
Information
Mathematika , Volume 5 , Issue 1 , June 1958 , pp. 49 - 57
Copyright
Copyright © University College London 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 49 note * Canadian J. of Math., 9 (1957), 305–312.

page 51 note * It will be noted that, as a consequence of these results, the form δT (n) satisfies an identity similar to (12a) but with a numerical factor independent of a 1,…, a m. This property characterizes the forms T (n)(a), considered in the present paper, among a wider class of symmetric forms.

page 56 note * Hardy, Littlewood and Póya, Inequalities (1st ed.), Theorem 52.