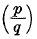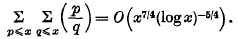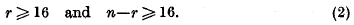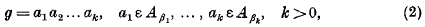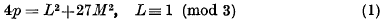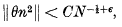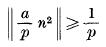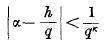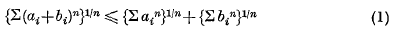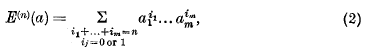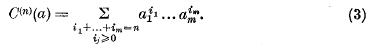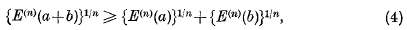Contents
Research Article
On the averages of some arithmetical functions of two variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-7
-
- Article
- Export citation
Indefinite quadratic forms in many variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 8-12
-
- Article
- Export citation
A proof of the subgroup theorem for free products
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-19
-
- Article
- Export citation
Criteria for cubic and quartic residuacity
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-29
-
- Article
- Export citation
An extension of a theorem of Heilbronn
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-37
-
- Article
- Export citation
On sequences of integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-39
-
- Article
- Export citation
The p-adic generalization of the Thue-Siegel-Roth theorem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-48
-
- Article
- Export citation
Some inequalities concerning symmetric forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-57
-
- Article
- Export citation
Derivatives of vector-valued functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-61
-
- Article
- Export citation
Note on a conformal transformation
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-66
-
- Article
- Export citation
Stress relief in a cracked plate
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-81
-
- Article
- Export citation
The separation of a viscous liquid at a straight edge
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-84
-
- Article
- Export citation
Front matter
MTK volume 5 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
-
- Article
-
- You have access
- Export citation