Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T19:20:25.241Z Has data issue: false hasContentIssue false
  • English
  • Français

THE VOLUME OF RANDOM POLYTOPES CIRCUMSCRIBED AROUND A CONVEX BODY

Part of: General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  22 June 2015

Ferenc Fodor ,
Daniel Hug  and
Ines Ziebarth
Ferenc Fodor
Affiliation:
Department of Geometry, Bolyai Institute, University of Szeged, Aradi vértanúk tere 1, 6720 Szeged, Hungary Department of Mathematics and Statistics, University of Calgary, Canada email fodorf@math.u-szeged.hu
Daniel Hug
Affiliation:
Karlsruhe Institute of Technology, Department of Mathematics, D-76128 Karlsruhe, Germany email daniel.hug@kit.edu
Ines Ziebarth
Affiliation:
Karlsruhe Institute of Technology, Department of Mathematics, D-76128 Karlsruhe, Germany email ines.ziebarth@gmail.com
Get access

Abstract

Let 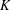$K$ be a convex body in 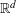$\mathbb{R}^{d}$ which slides freely in a ball. Let 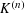$K^{(n)}$ denote the intersection of $n$ closed half-spaces containing 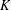$K$ whose bounding hyperplanes are independent and identically distributed according to a certain prescribed probability distribution. We prove an asymptotic formula for the expectation of the difference of the volumes of 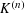$K^{(n)}$ and 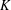$K$, and an asymptotic upper bound on the variance of the volume of 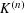$K^{(n)}$. We obtain these asymptotic formulas by proving results for weighted mean width approximations of convex bodies that admit a rolling ball by inscribed random polytopes and then using polar duality to convert them into statements about circumscribed random polytopes.

MSC classification

Primary: 52A22: Random convex sets and integral geometry
Secondary: 60D05: Geometric probability and stochastic geometry 52A27: Approximation by convex sets
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 283 - 306
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bárány, I., Random points and lattice points in convex bodies. Bull. Amer. Math. Soc. (N.S.) 45(3) 2008, 339–365.CrossRefGoogle Scholar
Böröczky, K. J., Fodor, F. and Hug, D., The mean width of random polytopes circumscribed around a convex body. J. Lond. Math. Soc. (2) 81(2) 2010, 499–523.CrossRefGoogle Scholar
Böröczky, K. J., Fodor, F., Reitzner, M. and Vígh, V., Mean width of random polytopes in a reasonably smooth convex body. J. Multivariate Anal. 100(10) 2009, 2287–2295.CrossRefGoogle Scholar
Böröczky, K. J. and Schneider, R., The mean width of circumscribed random polytopes. Canad. Math. Bull. 53(4) 2010, 614–628.CrossRefGoogle Scholar
Calka, P., Schreiber, T. and Yukich, J. E., Brownian limits, local limits and variance asymptotics for convex hulls in the ball. Ann. Probab. 41(1) 2013, 50–108.CrossRefGoogle Scholar
Calka, P. and Yukich, J. E., Variance asymptotics for random polytopes in smooth convex bodies. Probab. Theory Related Fields 158(1–2) 2014, 435–463.CrossRefGoogle Scholar
Federer, H., Geometric Measure Theory, Springer (Berlin, 1969).Google Scholar
Fodor, F., Hug, D. and Ziebarth, I., The volume of random polytopes circumscribed around a convex body. Preprint, 2014, arXiv:1409.8105.CrossRefGoogle Scholar
Glasauer, S. and Gruber, P. M., Asymptotic estimates for best and stepwise approximation of convex bodies. III. Forum Math. 9(4) 1997, 383–404.CrossRefGoogle Scholar
Gruber, P. M., Expectation of random polytopes. Manuscripta Math. 91(3) 1996, 393–419.CrossRefGoogle Scholar
Gruber, P. M., Convex and Discrete Geometry (Grundlehren der Mathematischen Wissenschaften 336), Springer (Berlin, 2007).Google Scholar
Hug, D., Contributions to affine surface area. Manuscripta Math. 91(1) 1996, 283–301.CrossRefGoogle Scholar
Hug, D., Curvature relations and affine surface area for a general convex body and its polar. Results Math. 29(3–4) 1996, 233–248.CrossRefGoogle Scholar
Hug, D., Absolute continuity for curvature measures of convex sets I. Math. Nachr. 195 1998, 139–158.CrossRefGoogle Scholar
Hug, D., Measures, curvatures and currents in convex geometry. Habilitationsschrift, University of Freiburg, 2000.Google Scholar
Hug, D., Random polytopes. In Stochastic Geometry, Spatial Statistics and Random Fields (Lecture Notes in Mathematics 2068), Springer (Heidelberg, 2013), 205–238.CrossRefGoogle Scholar
Hug, D. and Schneider, R., Hölder continuity of normal cycles and of support measures of convex bodies. Preprint, 2013, arXiv:1310.1514v1.Google Scholar
Kaltenbach, F. J., Asymptotisches Verhalten zufälliger konvexer Polyeder, Doctoral Thesis, Albert-Ludwigs-Universität Freiburg, 1990.Google Scholar
Reitzner, M., Random polytopes and the Efron–Stein jackknife inequality. Ann. Probab. 31(4) 2003, 2136–2166.CrossRefGoogle Scholar
Reitzner, M., Stochastic approximation of smooth convex bodies. Mathematika 51(1–2) 2004, 11–29.CrossRefGoogle Scholar
Reitzner, M., Random polytopes. In New Perspectives in Stochastic Geometry, Oxford University Press (Oxford, 2010), 45–76.Google Scholar
Rényi, A. and Sulanke, R., Über die konvexe Hülle von n zufällig gewählten Punkten. Z. Wahrsch. verw. Gebiete 2 1963, 75–84 (in German).CrossRefGoogle Scholar
Rényi, A. and Sulanke, R., Über die konvexe Hülle von n zufällig gewählten Punkten. II. Z. Wahrsch. verw. Gebiete 3 1964, 138–147 (in German).CrossRefGoogle Scholar
Schneider, R., Convex Bodies: the Brunn–Minkowski Theory, 2nd edn., (Encyclopedia of Mathematics and its Applications 151), Cambridge University Press (Cambridge, 2014).Google Scholar
Schneider, R. and Weil, W., Stochastic and Integral Geometry. In Probability and its Applications (New York), Springer (Berlin, 2008).Google Scholar
Schneider, R. and Wieacker, J. A., Random polytopes in a convex body. Z. Wahrsch. verw. Gebiete 52(1) 1980, 69–73.CrossRefGoogle Scholar
Spivak, M., A Comprehensive Introduction to Differential Geometry, Vol. 3, 2nd edn., Publish or Perish (Berkeley, CA, 1979).Google Scholar
Weil, W. and Wieacker, J. A., Stochastic geometry. In Handbook of Convex Geometry, Vol. A, B, North-Holland (Amsterdam, 1993), 1391–1438.CrossRefGoogle Scholar
Ziezold, H., Über die Eckenanzahl zufälliger konvexer Polygone. Izv. Akad. Nauk Armjan. SSR Ser. Mat. 5(3) 1970, 296–312 (in German, with Armenian and Russian summaries).Google Scholar