Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T22:30:08.191Z Has data issue: false hasContentIssue false
  • English
  • Français

The average orders of Hooley's Δr-functions

Published online by Cambridge University Press:  26 February 2010

R. R. Hall  and
G. Tenenbaum
R. R. Hall
Affiliation:
Department of Mathematics, University of York, Heslington, York. YO1 5DD
G. Tenenbaum
Affiliation:
UER Sciences Mathématiques, Université de Nancy 1, Boîte Postale 239, 54506 Vandoeuvre les Nancy Cedex, France.
Get access

Extract

In this paper we are concerned with upper bounds for the sums

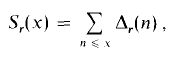
where

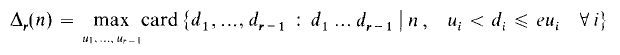
and Δ2(n) is written simply as Δ(n). These functions were introduced by Hooley [4] and applied in a novel way to problems related to Waring's, and in Diophantine approximation. Thus Hooley deduced from his result about S2(x) that for any irrational θ, real γ, and fixed ε > 0, the inequality

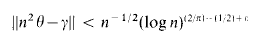
holds for infinitely many n. His result for S3(x) led to a proof that

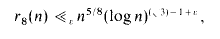
where r8(n) denotes the number of representations of n as the sum of eight positive cubes.

Type
Research Article
Information
Mathematika , Volume 31 , Issue 1 , June 1984 , pp. 98 - 109
Copyright
Copyright © University College London 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Feller, W.. An introduction to probability theory and its applications, Vol. II (John Wiley, New York, 1966).Google Scholar
2.Hall, R. R. and Tenenbaum, G.. On the average and normal orders of Hooley's Δ-function. J. London Math. Soc., (2), 25 (1982), 329–406.Google Scholar
3.Hall, R. R.. On the probability that n and f(n) are relatively prime III. Acta Arith., 20 (1972), 226–289.CrossRefGoogle Scholar
4.Hooley, C.. On a new technique and its applications to the theory of numbers. Proc. London Math. Soc., (3), 38 (1979), 115–151.CrossRefGoogle Scholar
5.Hooley, C.. On power-free values of polynomials II. Journal für die reine und angewandte Mathematik, 295 (1977), 1–21.Google Scholar
6.Pearson, K.. The Problem of the Random Walk. Nature, 72 (1905), 294–342.Google Scholar
7.Watson, G. N.. A treatise on the theory of Bessel functions. 2nd ed. (Cambridge, 1958).Google Scholar