Let Λ be a lattice in three-dimensional space with the property that the spheres of radius 1 centred at the points of Λ cover the whole of space. In other words, every point of space is at a distance not more than 1 from some point of Λ. It was proved by Bambah that then

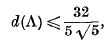
equality occurring if and only if Λ is a body-centred cubic lattice with the side of the cube equal to 4/√5. Another way of stating the result is to say that the least density of covering of three-dimensional space by equal spheres, subject to the condition that the centres of the spheres form a lattice, is 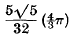. Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.