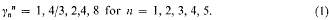Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watson, G. L.
1971.
On the minimum points of a positive quadratic form.
Mathematika,
Vol. 18,
Issue. 1,
p.
60.
Ryshkov, S. S.
and
Baranovskii, E. P.
1987.
Perfect lattices as admissible centerings.
Journal of Soviet Mathematics,
Vol. 37,
Issue. 4,
p.
1155.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
1988.
Low-dimensional lattices. III. Perfect forms.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 418,
Issue. 1854,
p.
43.
Jaquet-Chiffelle, David-Olivier
1992.
Description des voisines de E 7 ,D 7 ,D 8 , et D 9 .
Journal de théorie des nombres de Bordeaux,
Vol. 4,
Issue. 2,
p.
273.