Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zarzuela, Santiago
1990.
A generalization of a theorem of Sharp on big Cohen-Macaulay modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 108,
Issue. 2,
p.
193.
Simon, Anne-Marie
1990.
Some homological properties of complete modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 108,
Issue. 2,
p.
231.
Bruns, Winfried
1992.
The Evans-Griffith syzygy theorem and Bass numbers.
Proceedings of the American Mathematical Society,
Vol. 115,
Issue. 4,
p.
939.
Ali Esmkhani, Mohammad
and
Tousi, Massoud
2010.
Duality for a Cohen–Macaulay Local Ring.
Communications in Algebra,
Vol. 38,
Issue. 6,
p.
2048.

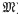 ) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated
) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated