Contents
Research Article
Homogeneous quadratic equations
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-4
-
- Article
- Export citation
An extension of stone's partitioning theorem for ordered sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 5-7
-
- Article
- Export citation
Fractional powers of a submodule of an algebra
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 8-13
-
- Article
- Export citation
The existence and uniqueness of a similarity solution of boundary-layer theory
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-19
-
- Article
- Export citation
Short surface waves due to an oscillating half-immersed sphere
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-39
-
- Article
- Export citation
On the distribution of Fekete points II
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-49
-
- Article
- Export citation
A convex body with a false centre is an ellipsoid
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-59
-
- Article
- Export citation
On the minimum points of a positive quadratic form
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-70
-
- Article
- Export citation
On pseudo-polynomials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-77
-
- Article
- Export citation
The lengths of limbs of random trees
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-81
-
- Article
- Export citation
Toroidal maps with prescribed types of vertices and faces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-90
-
- Article
- Export citation
On plane coverings with convex domains
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-97
-
- Article
- Export citation
On the representation of positive integers as sums of three cubes of positive rational numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-99
-
- Article
- Export citation
A determinant of linear forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 100-104
-
- Article
- Export citation
Symmetrical sets of constant width and their partitions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-111
-
- Article
- Export citation
A compact set of disjoint line segments in E3 whose end set has positive measure
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 112-125
-
- Article
- Export citation
On a problem of Gauthier
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 126-129
-
- Article
- Export citation
A note on the steady longitudinal motion of an insulating cylinder in a conducting fluid
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 130-133
-
- Article
- Export citation
When is a linear viscoelastic material elastic?
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-137
-
- Article
- Export citation
Trees with Hamiltonian square
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-140
-
- Article
- Export citation
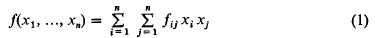

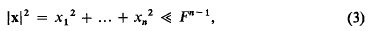
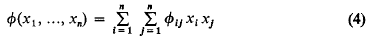

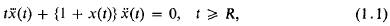
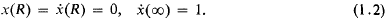

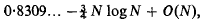

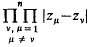



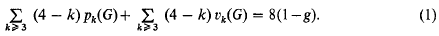
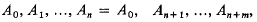
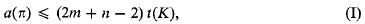

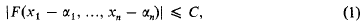
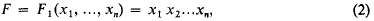
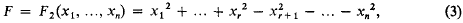

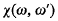 is called the distance between ω and ω′ in the spherical or in the chordal metric.
is called the distance between ω and ω′ in the spherical or in the chordal metric.