Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T23:59:56.635Z Has data issue: false hasContentIssue false
  • English
  • Français

Accelerating Copper Dissociated Dislocations to Transonic and Supersonic Speeds

Published online by Cambridge University Press:  01 February 2011

Paulo Sergio Branicio ,
Hélio Tsuzuki  and
José Pedro Rino
Paulo Sergio Branicio
Affiliation:
branicio@ihpc.a-star.edu.sg, Institute of High Performance Computing, Materials Theory and Simulation Laboratory, Singapore, Singapore
Hélio Tsuzuki
Affiliation:
helio@df.ufscar.br, Universidade Federal de São Carlos, Departamento de Física, São Carlos, SP, Brazil
José Pedro Rino
Affiliation:
djpr@df.ufscar.br, Universidade Federal de São Carlos, Departamento de Física, São Carlos, SP, Brazil
Get access

Abstract

The acceleration of dissociated dislocations to transonic and supersonic velocities in copper fcc crystals is investigated using molecular dynamics simulations. A thin and long system with a single stationary dislocation is constructed to study the dislocation acceleration process in anisotropic materials, which have two transverse, νT1 and νT2 , and one longitudinal acoustic velocity, νL along the dislocation glide direction. Copper is used as the representative anisotropic material and the embedded atom model is used to calculate interatomic forces. The common neighborhood parameter and local stresses are used to monitor the position and structure of the dislocations. Initial stationary dislocations on the (111) plane, aligned along the 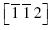direction are accelerated in the 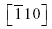direction in two different ways. By using the shear stress of a homogeneously sheared simulation box, and by using a strain-rate deformation obtained by shearing the top and bottom atomic layers in opposite directions by a given velocity. Results show that different levels of stress make dislocations accelerate and move in three distinguished regimes: i) in a plateau of velocities close to 1.6 km/s in the subsonic regime just below νT1; ii) in a narrow range of velocities around 2.6 km/s in the first transonic regime between νT1 and νT2; iii) in the second transonic regime, above νT2 but below νL, with increasing velocities for increasing stresses. Supersonic dislocations moving above νL are generated but their motion is transient. To be generated, they require high stresses above the shear strength which trigger spontaneous nucleation of dislocation dipoles throughout the system. The stacking fault width fluctuates around 35 Å in the subsonic regime but decline subsequently with velocity and fluctuates around 13 Å in the second transonic regime. In the first transonic regime however the stacking fault anomalously increases with velocity. Both the decreasing stacking fault width for fast dislocations and the plateau of velocities in the first transonic regime, indicating the existence of a radiation-free state, are in agreement with theoretical predictions.

Keywords

defectsdislocationssimulation
Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 1137: Symposium EE – Nano-and Microscale Materials–Mechanical Properties and Behavior under Extreme Environments , 2008 , 1137-EE08-08-W10-08
Copyright
Copyright © Materials Research Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1. Eshelby, J. D., Proc. Phys. Soc. Lond. A 62 (353), 307 (1949).Google Scholar
2. Gumbsch, P. and Gao, H., Science 283 (5404), 965 (1999);Google Scholar
Gumbsch, P. and Gao, H. J., J. Comput.-Aid. Mat. Des. 6 (2–3), 137 (1999);Google Scholar
Vandersall, J. A. Y. and Wirth, B. D., Phil. Mag. 84 (35), 3755 (2004).Google Scholar
3. Li, Q. K. and Shi, S. Q., Appl. Phys. Lett. 80 (17), 3069 (2002).Google Scholar
4. Teutonico, L. J., Phys. Rev. 124 (4), 1039 (1961);Google Scholar
Teutonico, L. J., Acta Metallurgica 11 (12), 1283 (1963).Google Scholar
5. Hirth, John Price and Lothe, Jens, Theory of dislocations, 2nd ed. (Krieger Pub. Co., Malabar, FL, 1992).Google Scholar
6. Mordehai, D., Ashkenazy, Y., Kelson, I. et al., Phys. Rev. B 67 (2), 024112 (2003);Google Scholar
Mordehai, D., Kelson, I., and Makov, G., Phys. Rev. B 74 (18), 184115 (2006).Google Scholar
7. Tsuzuki, H., Branicio, P. S., and Rino, J. P., Appl. Phys. Lett. 92 (19), 191909 (2008);Google Scholar
Tsuzuki, H., Branicio, P. S., and Rino, J. P., Acta Mater (2009), doi:10.1016/j.actamat.2008.12.025.Google Scholar
8. Mishin, Y., Mehl, M. J., Papaconstantopoulos, D. A. et al., Phys. Rev. B 63 (22), 224106 (2001).Google Scholar
9. Tsuzuki, H., Branicio, P. S., and Rino, J. P., Comput. Phys. Commun. 177 (6), 518 (2007).Google Scholar