Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-22T11:53:12.041Z Has data issue: false hasContentIssue false
  • English
  • Français

FORMAL LIFTING OF DUALIZING COMPLEXES AND CONSEQUENCES

Part of: Ring extensions and related topics Arithmetic rings and other special rings

Published online by Cambridge University Press:  20 January 2025

SHIJI LYU Open the ORCID record for SHIJI LYU [Opens in a new window]
SHIJI LYU*
Affiliation:
Department of Mathematics, Statistics, and Computer Science University of Illinois Chicago Chicago, IL 60607-7045 United States
*
slyu@uic.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for a Noetherian ring A that is I-adically complete for an ideal I, if 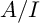$A/I$ admits a dualizing complex, so does A. This gives an alternative proof of the fact that a Noetherian complete local ring admits a dualizing complex. We discuss several consequences of this result. We also consider a generalization of the notion of dualizing complexes to infinite-dimensional rings and prove the results in this generality. In addition, we give an alternative proof of the fact that every excellent Henselian local ring admits a dualizing complex, using ultrapower.

Keywords

dualizing complexeslifting problemexcellence properties

MSC classification

Primary: 13F40: Excellent rings
Secondary: 13B35: Completion
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aoyama, Y., Some basic results on canonical modules , J. Math. Kyoto Univ. 23 (1983), no. 1, 85–94.Google Scholar
Bhatt, B., Algebraization and Tannaka duality , Cambridge J. Math. 4 (2016), no. 4, 403–461.CrossRefGoogle Scholar
Česnavičius, K., Macaulayfication of Noetherian schemes , Duke Math. J. 170 (2021), no. 7, 1419–1455.CrossRefGoogle Scholar
Fossum, R., Foxby, H. B., Griffith, P., and Reiten, I., Minimal injective resolutions with applications to dualizing modules and Gorenstein modules , Inst. Hautes Études Sci. Publ. Math. 45 (1976), 193–215.CrossRefGoogle Scholar
Ferrand, D. and Raynaud, M., Fibres formelles d’un anneau local noethérien , Annales scientifiques de l’É.N.S. 4e série 3 (1970), no. 3, 295–311.Google Scholar
Greco, S. and Marinari, M. G., Nagata’s criterion and openness of loci for Gorenstein and complete intersection , Math. Z. 160 (1978), 207–216.CrossRefGoogle Scholar
Greco, S., A note on universally catenary rings , Nagoya Math. J. 87 (1982), 95–100.CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Seconde partie , Inst. Hautes Études Sci. Publ. Math. 24 (1965), 55–231, with a collaboration of Jean Dieudonné.Google Scholar
Hall, J. A., Fundamental dualizing complexes for commutative Noetherian rings , Quart J. Math. Oxford 30 (1979), no. 2, 21–32.CrossRefGoogle Scholar
Hartshorne, R., Residues and duality, Lecture Notes in Mathematics, 20, Springer-Verlag, Berlin, 1966.CrossRefGoogle Scholar
Hinich, V., Rings with approximation property admit a dualizing complex , Math. Nachr. 163 (1993), 289–296.CrossRefGoogle Scholar
Hochster, M., Non-openness of loci in Noetherian rings , Duke Math. J. 40 (1973), no. 1, 215–219.CrossRefGoogle Scholar
Kawasaki, T., On arithmetic Macaulayfication of Noetherian rings , Trans. Amer. Math. Soc. 354 (2002), no. 1, 123–149.CrossRefGoogle Scholar
Kawasaki, T., Finiteness of Cousin cohomologies , Trans. Amer. Math. Soc. 360 (2008), no. 5, 2709–2739.CrossRefGoogle Scholar
Kurano, K. and Shimomoto, K., Ideal-adic completion of quasi-excellent rings (after Gabber) , Kyoto J. Math. 61 (2021), no. 3, 707–722.CrossRefGoogle Scholar
Lurie, J., Spectral algebraic geometry, https://www.math.ias.edu/lurie/papers/SAG-rootfile.pdf Google Scholar
Lyu, S., Permanence properties of splinters via ultrapower , Michigan Math. J. Advance Publication, (2024), 1–8.Google Scholar
Marot, J., Sur les anneaux universellement japonais , Bull. Soc. Math. France 103 (1975), 103–111.CrossRefGoogle Scholar
Takumi, M., A uniform treatment of Grothendieck’s localization problem , Compos. Math. 158 (2022), no. 1, 57–88.Google Scholar
Nishimura, J., A few examples of local rings, I , Kyoto J. Math. 52 (2012), no. 1, 51–87.CrossRefGoogle Scholar
Ogoma, T., Existence of dualizing complexes , J. Math. Kyoto Univ. 24 (1984), no. 1, 27–48.Google Scholar
Reiten, I., The converse to a theorem of Sharp on Gorenstein modules , Proc. Amer. Math. Soc 32 (1972), 417–420.CrossRefGoogle Scholar
Schoutens, H., The use of ultraproducts in commutative algebra, Lecture Notes in Mathematics, 1999, Springer-Verlag, Berlin, 2010.CrossRefGoogle Scholar
Sharp, R. Y., A commutative Noetherian ring which possesses a dualizing complex is acceptable , Math. Proc. Camb. Phil. Soc. 82 (1977), 192–213.CrossRefGoogle Scholar
The Stacks Project Authors, The Stacks project, https://stacks.math.columbia.edu/ Google Scholar