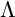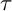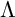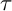1 Introduction
The representation theory of a finite-dimensional algebra
![]() $ \Lambda $
aims to understand the category of finitely generated
$ \Lambda $
aims to understand the category of finitely generated
![]() $ \Lambda $
-modules. A fundamental step in achieving a complete understanding is the investigation of the indecomposable finite-dimensional modules: these are the building blocks of the category.
$ \Lambda $
-modules. A fundamental step in achieving a complete understanding is the investigation of the indecomposable finite-dimensional modules: these are the building blocks of the category.
Some algebras have only a finite number of indecomposables, up to isomorphism. These representation-finite algebras are the best understood: powerful techniques were developed to distinguish representation-finite algebras from representation-infinite ones and several equivalent characterizations of this property were obtained.
On the other hand, representation-infinite algebras exhibit in most cases a wild behavior, to the point where an explicit classification of all the indecomposables seems out of reach.
Nonetheless, these more complex module categories have many interesting characteristics and there are many valid approaches to their study.
A useful tool is the idea of torsion pairs, introduced by Dickson in 1966 as a generalization of torsion abelian groups to arbitrary abelian categories. Torsion pairs give a way to break a complex category into two smaller pieces, a torsion and a torsion-free class, from which the whole can be recovered.
Therefore, understanding the set of torsion pairs in the category of finite-dimensional modules would be an important step toward a more complete understanding of representation-infinite algebras.
Among the torsion pairs in the category of finite-dimensional modules, we find the functorially finite pairs, which are generated, in a suitable sense, by a single module, known as a support
![]() $ \tau $
-tilting module.
$ \tau $
-tilting module.
The concept of
![]() $ \tau $
-tilting module was introduced by Adachi, Iyama, and Reiten [Reference Adachi, Iyama and Reiten1] to complete, with respect to mutation, the classical theory of tilting modules.
$ \tau $
-tilting module was introduced by Adachi, Iyama, and Reiten [Reference Adachi, Iyama and Reiten1] to complete, with respect to mutation, the classical theory of tilting modules.
In their foundational work, they established a bijection between functorially finite torsion classes and support
![]() $ \tau $
-tilting modules.
$ \tau $
-tilting modules.
Demonet, Iyama, and Jasso introduced in [Reference Demonet, Iyama and Jasso14]
![]() $ \tau $
-tilting finite algebras: these are finite-dimensional algebras which admit a finite number of basic
$ \tau $
-tilting finite algebras: these are finite-dimensional algebras which admit a finite number of basic
![]() $ \tau $
-tilting modules up to isomorphism.
$ \tau $
-tilting modules up to isomorphism.
In the cited work, they obtained a connection between bricks, that is, modules whose endomorphism ring is a division ring, torsion classes, and
![]() $ \tau $
-tilting modules.
$ \tau $
-tilting modules.
In particular, they proved that a finite-dimensional algebra is
![]() $ \tau $
-tilting finite if and only if it has a finite number of finitely generated bricks up to isomorphism.
$ \tau $
-tilting finite if and only if it has a finite number of finitely generated bricks up to isomorphism.
This result suggested a strong analogy between representation-finite algebras and
![]() $ \tau $
-tilting finite algebras, leading to new versions of classical results, where the role of indecomposable modules in the representation-finite case is now played by bricks.
$ \tau $
-tilting finite algebras, leading to new versions of classical results, where the role of indecomposable modules in the representation-finite case is now played by bricks.
As an example, in [Reference Schroll and Treffinger27], Schroll and Treffinger prove the analogue of the first Brauer–Thrall conjecture in this brick setting: for every
![]() $ \tau $
-tilting infinite algebra, we can find a succession of bricks
$ \tau $
-tilting infinite algebra, we can find a succession of bricks
![]() $ \{ B_n \}_{n \in \mathbb {N}} $
such that
$ \{ B_n \}_{n \in \mathbb {N}} $
such that
![]() $ \dim B_N \ge n $
.
$ \dim B_N \ge n $
.
The analogue of the second Brauer–Thrall conjecture claiming the existence of an infinite collection of Hom-orthogonal bricks for every
![]() $ \tau $
-tilting infinite algebras is still wide open.
$ \tau $
-tilting infinite algebras is still wide open.
Following this line, the aim of this paper is to prove a brick version of the following classical result of Auslander.
Theorem 1.1 [Reference Auslander7].
An Artin algebra
![]() $ \Lambda $
is representation-finite if and only if every indecomposable module is finitely generated.
$ \Lambda $
is representation-finite if and only if every indecomposable module is finitely generated.
To obtain this, we exploit the concept of torsion-free, almost torsion module, introduced by Herzog in [Reference Herzog19] and recently reintroduced by Barnard, Carrol, and Zhu [Reference Barnard, Carroll and Zhu8] in the finite-dimensional setting.
These modules play an important role within the study of the lattice structure of the set of torsion classes in the category of finitely generated modules over a finite-dimensional algebra. In [Reference Demonet, Iyama, Reading, Reiten and Thomas15], we find a detailed study of this lattice theoretical properties.
We start in §2 with a quick reminder about
![]() $ \tau $
-tilting theory, silting theory, and definable classes. We also recall a bijection, essentially due to Crawley–Boevey, between torsion-free classes in the category of finitely generated modules over a Noetherian ring and definable torsion-free classes in the large module category.
$ \tau $
-tilting theory, silting theory, and definable classes. We also recall a bijection, essentially due to Crawley–Boevey, between torsion-free classes in the category of finitely generated modules over a Noetherian ring and definable torsion-free classes in the large module category.
Section 3 contains a discussion of the concept of torsion-free, almost torsion module, with the new result that torsion-free, almost torsion modules determine definable torsion-free classes.
In §4, we observe that, for a non-
![]() $ \tau $
-tilting finite algebra, we can always find a non-functorially finite torsion class which is locally maximal (i.e., without any element covering it in the lattice of torsion classes).
$ \tau $
-tilting finite algebra, we can always find a non-functorially finite torsion class which is locally maximal (i.e., without any element covering it in the lattice of torsion classes).
We use this last observation to give the proof of the following brick version of the theorem of Auslander.
Theorem 1.2. A finite-dimensional algebra
![]() $ \Lambda $
is
$ \Lambda $
is
![]() $ \tau $
-tilting finite if and only if every brick over
$ \tau $
-tilting finite if and only if every brick over
![]() $ \Lambda $
is finitely generated.
$ \Lambda $
is finitely generated.
1.1 Notation
All the subcategories we consider are assumed to be full. We do not distinguish a collection of objects in a category from the corresponding full subcategory.
![]() $ R $
denotes an arbitrary ring (with unit),
$ R $
denotes an arbitrary ring (with unit),
![]() $ \Lambda $
a finite-dimensional algebra over some field
$ \Lambda $
a finite-dimensional algebra over some field
![]() $ k $
.
$ k $
.
We denote by
![]() $ R$
-Mod (resp. R-mod) the category of (finitely presented) left
$ R$
-Mod (resp. R-mod) the category of (finitely presented) left
![]() $ R $
modules.
$ R $
modules.
For a Grothendieck category
![]() $ \mathcal {G} $
, we denote by
$ \mathcal {G} $
, we denote by
![]() $ \mathcal {D}(\mathcal {G}) $
the derived category of
$ \mathcal {D}(\mathcal {G}) $
the derived category of
![]() $ \mathcal {G} $
. We also write
$ \mathcal {G} $
. We also write
![]() $ \mathcal {D}(R) $
instead of
$ \mathcal {D}(R) $
instead of
![]() $ \mathcal {D}(R$
-
$ \mathcal {D}(R$
-
![]() $\mathrm {Mod})$
.
$\mathrm {Mod})$
.
For a subclass
![]() $ \mathcal { C } \subseteq R$
-Mod, the symbol
$ \mathcal { C } \subseteq R$
-Mod, the symbol
![]() $ \mathbf {T}(\mathcal { C }) $
(resp.
$ \mathbf {T}(\mathcal { C }) $
(resp.
![]() $ \mathbf {F}(\mathcal { C }) $
) denotes the smallest torsion (resp. torsion-free) class in
$ \mathbf {F}(\mathcal { C }) $
) denotes the smallest torsion (resp. torsion-free) class in
![]() $ R$
-Mod containing
$ R$
-Mod containing
![]() $ \mathcal { C } $
.
$ \mathcal { C } $
.
If
![]() $ \mathcal {C} = \{M\} $
, we write simply
$ \mathcal {C} = \{M\} $
, we write simply
![]() $ \mathbf {T}(M) $
and
$ \mathbf {T}(M) $
and
![]() $ \mathbf {F}(M) $
.
$ \mathbf {F}(M) $
.
We use
![]() $ \widetilde {\mathbf {T}} $
(resp.
$ \widetilde {\mathbf {T}} $
(resp.
![]() $ \widetilde {\mathbf {F}} $
) in the same way when referring to torsion pairs in
$ \widetilde {\mathbf {F}} $
) in the same way when referring to torsion pairs in
![]() $ R$
-mod.
$ R$
-mod.
![]() $ \mathbf { Tors }(R) $
(resp.
$ \mathbf { Tors }(R) $
(resp.
![]() $ \mathbf { tors }(R) $
) is the class of torsion classes in
$ \mathbf { tors }(R) $
) is the class of torsion classes in
![]() $ R$
-Mod (resp.
$ R$
-Mod (resp.
![]() $ R$
-mod).
$ R$
-mod).
For a class
![]() $ \mathcal {S} \subseteq R$
-
$ \mathcal {S} \subseteq R$
-
![]() $\mathrm {Mod} $
,
$\mathrm {Mod} $
,
![]() $ \mathrm {Gen}(\mathcal {S}) $
is the subcategory of modules isomorphic to quotients of arbitrary (set-indexed) direct sums of objects in
$ \mathrm {Gen}(\mathcal {S}) $
is the subcategory of modules isomorphic to quotients of arbitrary (set-indexed) direct sums of objects in
![]() $ \mathcal {S} $
.
$ \mathcal {S} $
.
Let
![]() $ I \subset \mathbb {N} $
denote by
$ I \subset \mathbb {N} $
denote by
![]() $ M^{\perp _I} $
the class of modules
$ M^{\perp _I} $
the class of modules
![]() $ N $
with
$ N $
with
![]() $ \operatorname {Ext}^i(M,N) = 0 $
, for all
$ \operatorname {Ext}^i(M,N) = 0 $
, for all
![]() $ i \in I $
. In case the set
$ i \in I $
. In case the set
![]() $ I = \{i\} $
, we write
$ I = \{i\} $
, we write
![]() $ M^{\perp _i} $
.
$ M^{\perp _i} $
.
2 Preliminaries
We assume that the reader is familiar with the concept of torsion pair. A comprehensive account can be found in many textbooks, for instance, [Reference Borceux9].
2.1
 $\tau $
-tilting finite algebras
$\tau $
-tilting finite algebras
We recall in this section the definition of a
![]() $ \tau $
-tilting module by Adachi, Iyama, and Reiten [Reference Adachi, Iyama and Reiten1] and the related concept of
$ \tau $
-tilting module by Adachi, Iyama, and Reiten [Reference Adachi, Iyama and Reiten1] and the related concept of
![]() $ \tau $
-tilting finiteness, together with some characterizations given in [Reference Angeleri Hügel, Marks and Vitória5], [Reference Demonet, Iyama and Jasso14].
$ \tau $
-tilting finiteness, together with some characterizations given in [Reference Angeleri Hügel, Marks and Vitória5], [Reference Demonet, Iyama and Jasso14].
Definition 2.1. Let
![]() $ \Lambda $
be a finite-dimensional algebra over a field
$ \Lambda $
be a finite-dimensional algebra over a field
![]() $ k $
. Denote by
$ k $
. Denote by
![]() $ \tau $
the Auslander–Reiten translation.
$ \tau $
the Auslander–Reiten translation.
![]() $ M \in \Lambda $
-
$ M \in \Lambda $
-
![]() $\mathrm {mod} $
is
$\mathrm {mod} $
is
![]() $\tau $
-tilting if:
$\tau $
-tilting if:
-
(τ1)
 $ \mathrm {Hom}(M, \tau M) = 0 $
;
$ \mathrm {Hom}(M, \tau M) = 0 $
; -
(τ2) The number of nonisomorphic indecomposable summands of
 $ M $
is equal to the number of isoclasses of simple
$ M $
is equal to the number of isoclasses of simple
 $ \Lambda $
-modules.
$ \Lambda $
-modules.
Given two
![]() $ \tau $
-tilting modules
$ \tau $
-tilting modules
![]() $ M_1 $
and
$ M_1 $
and
![]() $ M_2 $
, we say that
$ M_2 $
, we say that
![]() $ M_1 $
is equivalent to
$ M_1 $
is equivalent to
![]() $ M_2 $
if their additive closures in
$ M_2 $
if their additive closures in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
coincide,
$\mathrm {mod} $
coincide,
![]() $ \mathrm {add}(M_1) = \mathrm {add}(M_2)$
.
$ \mathrm {add}(M_1) = \mathrm {add}(M_2)$
.
A module
![]() $ M $
is support
$ M $
is support
![]() $\tau $
-tilting if there exists some idempotent
$\tau $
-tilting if there exists some idempotent
![]() $ e \in \Lambda $
, such that
$ e \in \Lambda $
, such that
![]() $ M $
is a
$ M $
is a
![]() $\tau $
-tilting
$\tau $
-tilting
![]() $\Lambda /\langle e\rangle $
-module.
$\Lambda /\langle e\rangle $
-module.
Definition 2.2. A finite-dimensional algebra
![]() $ \Lambda $
is
$ \Lambda $
is
![]() $\tau $
-tilting finite if there are only finitely many basic
$\tau $
-tilting finite if there are only finitely many basic
![]() $ \tau $
-tilting
$ \tau $
-tilting
![]() $ \Lambda $
-modules up to isomorphism.
$ \Lambda $
-modules up to isomorphism.
Definition 2.3. A
![]() $ \Lambda $
-module
$ \Lambda $
-module
![]() $ B $
is a brick if its endomorphism ring is a skew field.
$ B $
is a brick if its endomorphism ring is a skew field.
Definition 2.4. Let
![]() $ \mathbf {s} $
be a subcategory of
$ \mathbf {s} $
be a subcategory of
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
,
$\mathrm {mod} $
,
![]() $ M \in \Lambda $
-
$ M \in \Lambda $
-
![]() $\mathrm {mod} $
. A morphism
$\mathrm {mod} $
. A morphism
![]() $ r : S \to M $
is a right
$ r : S \to M $
is a right
![]() $ \mathbf {s}$
-approximation if
$ \mathbf {s}$
-approximation if
![]() $ S \in \mathbf {s} $
and for every
$ S \in \mathbf {s} $
and for every
![]() $ f : S' \to M $
with
$ f : S' \to M $
with
![]() $ S' \in \mathbf {s} $
there exists a map
$ S' \in \mathbf {s} $
there exists a map
![]() $ \bar {f} : S' \to S $
such that
$ \bar {f} : S' \to S $
such that
![]() $ f = r \circ \bar {f} $
. Dually, we can define a left
$ f = r \circ \bar {f} $
. Dually, we can define a left
![]() $ \mathbf {s}$
-approximation.
$ \mathbf {s}$
-approximation.
A subcategory
![]() $ \mathbf {s} $
of
$ \mathbf {s} $
of
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
is functorially finite if every module admits a left and right
$\mathrm {mod} $
is functorially finite if every module admits a left and right
![]() $ \mathbf {s}$
-approximation.
$ \mathbf {s}$
-approximation.
Theorem 2.5 ([Reference Demonet, Iyama and Jasso14, Ths. 3.8 and 4.2]).
The following conditions are equivalent for a finite-dimensional algebra
![]() $ \Lambda $
:
$ \Lambda $
:
-
(TF1)
 $ \Lambda $
is
$ \Lambda $
is
 $\tau $
-tilting finite.
$\tau $
-tilting finite. -
(TF2)
 $ \mathbf {tors}(\Lambda ) $
is finite.
$ \mathbf {tors}(\Lambda ) $
is finite. -
(TF3) All torsion classes in
 $ \Lambda $
-
$ \Lambda $
-
 $\mathrm {mod} $
are functorially finite.
$\mathrm {mod} $
are functorially finite. -
(TF4) There are only finitely many isoclasses of bricks in
 $\Lambda $
-
$\Lambda $
-
 $\mathrm {mod} $
.
$\mathrm {mod} $
.
For the next characterization, we recall the concept of silting module, introduced in [Reference Angeleri Hügel, Marks and Vitória4].
Definition 2.6. Let
![]() $ R $
be a ring.
$ R $
be a ring.
Let
![]() $ \sigma $
be a homomorphism in
$ \sigma $
be a homomorphism in
![]() $ \mathrm {Proj}(R) $
, the subcategory of
$ \mathrm {Proj}(R) $
, the subcategory of
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
whose objects are the projective modules. We define the class
$\mathrm {Mod} $
whose objects are the projective modules. We define the class
A module
![]() $ M \in R$
-
$ M \in R$
-
![]() $\mathrm {Mod} $
is called silting if there exists a projective presentation
$\mathrm {Mod} $
is called silting if there exists a projective presentation
![]() $ P \xrightarrow {\sigma } Q \to M \to 0 $
such that
$ P \xrightarrow {\sigma } Q \to M \to 0 $
such that
![]() $ \mathrm {Gen}(M) = \mathcal {D}_\sigma $
. Notice that in this case
$ \mathrm {Gen}(M) = \mathcal {D}_\sigma $
. Notice that in this case
![]() $ \mathcal {D}_\sigma $
is a torsion class in
$ \mathcal {D}_\sigma $
is a torsion class in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
.
$\mathrm {Mod} $
.
Two silting modules are said to be equivalent if they generate the same torsion class.
Proposition 2.7 [Reference Angeleri Hügel, Marks and Vitória4, Prop. 3.16].
A module
![]() $ M $
over a finite-dimensional algebra is support
$ M $
over a finite-dimensional algebra is support
![]() $ \tau $
-tilting if and only if it is a finite-dimensional silting module.
$ \tau $
-tilting if and only if it is a finite-dimensional silting module.
Theorem 2.8 [Reference Angeleri Hügel, Marks and Vitória5, Th. 4.8].
Let
![]() $ \Lambda $
be a finite-dimensional algebra. TFAE:
$ \Lambda $
be a finite-dimensional algebra. TFAE:
-
(i)
 $ \Lambda $
is
$ \Lambda $
is
 $ \tau $
-tilting finite.
$ \tau $
-tilting finite. -
(ii) For every
 $ \mathcal {T} \in \mathbf { Tors }(\Lambda ) $
, there is a finite-dimensional silting module
$ \mathcal {T} \in \mathbf { Tors }(\Lambda ) $
, there is a finite-dimensional silting module
 $ S $
, with
$ S $
, with
 $ \mathcal {T} = \mathrm {Gen}(S) $
.
$ \mathcal {T} = \mathrm {Gen}(S) $
. -
(iii) Every silting module is finite-dimensional up to equivalence.
There are dual notions of cosilting and
![]() $\tau ^{-}$
-tilting modules, with dual properties linked to torsion-free classes. See [Reference Angeleri Hügel and Hrbek3] for details and additional results about cosilting modules.
$\tau ^{-}$
-tilting modules, with dual properties linked to torsion-free classes. See [Reference Angeleri Hügel and Hrbek3] for details and additional results about cosilting modules.
2.2 Definable torsion and torsion-free classes
We collect some well-known facts about definable classes and purity. A comprehensive reference can be found in [Reference Prest24].
Definition 2.9. A short exact sequence
![]() $ 0 \to L \to M \to N \to 0 $
in
$ 0 \to L \to M \to N \to 0 $
in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
is pure if for every
$\mathrm {Mod} $
is pure if for every
![]() $ U \in R$
-
$ U \in R$
-
![]() $\mathrm {mod} $
the sequence
$\mathrm {mod} $
the sequence
is an exact sequence of abelian groups. In this case, we say that
![]() $ L $
is a pure submodule of
$ L $
is a pure submodule of
![]() $ M $
.
$ M $
.
Definition 2.10. Let
![]() $ \mathcal {D} \subseteq R$
-
$ \mathcal {D} \subseteq R$
-
![]() $\mathrm {Mod} $
. We say that
$\mathrm {Mod} $
. We say that
![]() $ \mathcal {D} $
is definable if it is closed under products, pure submodules, and direct limits.
$ \mathcal {D} $
is definable if it is closed under products, pure submodules, and direct limits.
Remark 2.11. Notice that a torsion-free class in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
is definable if and only if it is closed under direct limits, as closure under products and (pure) submodules is granted.
$\mathrm {Mod} $
is definable if and only if it is closed under direct limits, as closure under products and (pure) submodules is granted.
For finite-dimensional algebras, we have the following.
Proposition 2.12 [Reference Crawley-Boevey12, Sec. 2.2].
A short exact sequence
![]() $ 0 \to L \to M \to N \to 0 $
in
$ 0 \to L \to M \to N \to 0 $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
is pure if for every
$\mathrm {Mod} $
is pure if for every
![]() $ U \in \Lambda $
-
$ U \in \Lambda $
-
![]() $\mathrm {mod} $
the sequence
$\mathrm {mod} $
the sequence
is an exact sequence of abelian groups.
Examples 2.13.
-
(1) Let
 $ M \in R$
-
$ M \in R$
-
 $\mathrm {mod} $
. Then the torsion-free class
$\mathrm {mod} $
. Then the torsion-free class
 $ M^{\perp _0} $
is a definable subcategory of
$ M^{\perp _0} $
is a definable subcategory of
 $ R$
-
$ R$
-
 $\mathrm {Mod} $
.
$\mathrm {Mod} $
. -
(1’) Let
 $ M \in \Lambda $
-
$ M \in \Lambda $
-
 $\mathrm {mod} $
. Then, as shown in [Reference Dean13, Exam. 2.3], the torsion class
$\mathrm {mod} $
. Then, as shown in [Reference Dean13, Exam. 2.3], the torsion class
 $ {}^{\perp _0}M $
is a definable subcategory of
$ {}^{\perp _0}M $
is a definable subcategory of
 $ \Lambda $
-
$ \Lambda $
-
 $\mathrm {Mod} $
.
$\mathrm {Mod} $
. -
(2) Given a set-indexed family of definable classes
 $ \{ \mathcal {D}_i \}_{i \in I} $
, the intersection
$ \{ \mathcal {D}_i \}_{i \in I} $
, the intersection
 $ \mathcal {D} = \bigcap _{i \in I} \mathcal {D}_i $
is a definable class.
$ \mathcal {D} = \bigcap _{i \in I} \mathcal {D}_i $
is a definable class.
We are concerned with definable torsion classes and definable torsion-free classes.
For definable torsion-free classes, we have a result valid for any Noetherian ring, using [Reference Crawley-Boevey11, Sec. 4.4]:
Theorem 2.14. Let
![]() $ R $
be a Noetherian ring. There is a bijection between torsion pairs in
$ R $
be a Noetherian ring. There is a bijection between torsion pairs in
![]() $ R$
-
$ R$
-
![]() $\mathrm {mod} $
and torsion pairs in
$\mathrm {mod} $
and torsion pairs in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
with definable torsion-free class.
$\mathrm {Mod} $
with definable torsion-free class.
This bijection associates to a torsion pair
![]() $ ( \mathbf {t}, \mathbf {f} ) $
in
$ ( \mathbf {t}, \mathbf {f} ) $
in
![]() $ R$
-
$ R$
-
![]() $\mathrm {mod} $
the limit closure
$\mathrm {mod} $
the limit closure
![]() $ ( \mathcal {T} := \underrightarrow {\lim }\, \mathbf {t},\, \mathcal {F} := \underrightarrow {\lim }\, \mathbf {f}) $
. In this setting,
$ ( \mathcal {T} := \underrightarrow {\lim }\, \mathbf {t},\, \mathcal {F} := \underrightarrow {\lim }\, \mathbf {f}) $
. In this setting,
![]() $ \mathcal { T } $
can also be described as
$ \mathcal { T } $
can also be described as
![]() $ \mathrm {Gen}(\mathbf {t}) $
and
$ \mathrm {Gen}(\mathbf {t}) $
and
![]() $ \mathcal {F} $
as the perpendicular class
$ \mathcal {F} $
as the perpendicular class
![]() $ \mathbf {t}^{\perp _0} $
.
$ \mathbf {t}^{\perp _0} $
.
The inverse of this map sends a torsion pair
![]() $ ( \mathcal {T} , \mathcal {F} ) $
to its restriction
$ ( \mathcal {T} , \mathcal {F} ) $
to its restriction
![]() $ ( \mathcal {T} \cap R$
-
$ ( \mathcal {T} \cap R$
-
![]() $\mathrm {mod}, \mathcal {F} \cap R$
-
$\mathrm {mod}, \mathcal {F} \cap R$
-
![]() $\mathrm {mod} ) $
.
$\mathrm {mod} ) $
.
A dual version of this bijection holds true in the setting of finite-dimensional algebras as a direct consequence of the following observation [Reference Crawley-Boevey12, Sec. 2.2].
Lemma 2.15. Let
![]() $ M \in \Lambda $
-
$ M \in \Lambda $
-
![]() $\mathrm {Mod} $
. Then
$\mathrm {Mod} $
. Then
![]() $ M $
is a pure submodule of the product of its finite-dimensional quotients.
$ M $
is a pure submodule of the product of its finite-dimensional quotients.
Proof. Let
![]() $ \mathcal {S} $
be a chosen set of representatives of all the isomorphism classes of finite-dimensional
$ \mathcal {S} $
be a chosen set of representatives of all the isomorphism classes of finite-dimensional
![]() $ \Lambda $
-modules. Let
$ \Lambda $
-modules. Let
![]() $ \overline {M} := \prod _{S \in \mathcal {S}} \prod _{f \in \operatorname {Hom}(M, S) } \operatorname {Im}(f) $
and consider the map
$ \overline {M} := \prod _{S \in \mathcal {S}} \prod _{f \in \operatorname {Hom}(M, S) } \operatorname {Im}(f) $
and consider the map
![]() $ f : M \to \overline {M} $
obtained through the universal property of products. Then, by construction, every map from
$ f : M \to \overline {M} $
obtained through the universal property of products. Then, by construction, every map from
![]() $ M $
to a finite-dimensional module must factor through
$ M $
to a finite-dimensional module must factor through
![]() $ f $
.
$ f $
.
In particular, the map
![]() $ f $
is injective: we have some set
$ f $
is injective: we have some set
![]() $ I $
such that there exists an embedding
$ I $
such that there exists an embedding
![]() $ g : M \to ( D\Lambda )^{I} $
; therefore, if
$ g : M \to ( D\Lambda )^{I} $
; therefore, if
![]() $ f(m) = 0 $
for some
$ f(m) = 0 $
for some
![]() $ m \in M $
, then
$ m \in M $
, then
![]() $ g_i(m) = 0 $
for all
$ g_i(m) = 0 $
for all
![]() $ i \in I $
, which means
$ i \in I $
, which means
![]() $ m = 0 $
.
$ m = 0 $
.
Using Proposition 2.12, we can conclude that
![]() $ f $
is a pure monomorphism.
$ f $
is a pure monomorphism.
Theorem 2.16. Let
![]() $ \Lambda $
be a finite-dimensional algebra over a field
$ \Lambda $
be a finite-dimensional algebra over a field
![]() $ k $
. There is a bijection between torsion pairs in
$ k $
. There is a bijection between torsion pairs in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
and torsion pairs in
$\mathrm {mod} $
and torsion pairs in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
with definable torsion class.
$\mathrm {Mod} $
with definable torsion class.
This bijection associates to a torsion pair
![]() $ ( \mathbf {t}, \mathbf {f} ) $
in
$ ( \mathbf {t}, \mathbf {f} ) $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
the torsion pair cogenerated by
$\mathrm {mod} $
the torsion pair cogenerated by
![]() $ \mathbf {f} ( \mathcal {T} := {}^{\perp _0}\mathbf {f},\, \mathcal {F} := ({}^{\perp _0}\mathbf {f})^{\perp _0}) $
. In this setting,
$ \mathbf {f} ( \mathcal {T} := {}^{\perp _0}\mathbf {f},\, \mathcal {F} := ({}^{\perp _0}\mathbf {f})^{\perp _0}) $
. In this setting,
![]() $ \mathcal { T } $
can also be described as
$ \mathcal { T } $
can also be described as
![]() $ \mathrm {PureCogen}(\mathbf {t}) $
, the class of modules obtained as pure submodules of arbitrary direct products of modules in
$ \mathrm {PureCogen}(\mathbf {t}) $
, the class of modules obtained as pure submodules of arbitrary direct products of modules in
![]() $ \mathbf {t} $
.
$ \mathbf {t} $
.
The inverse of this map sends a torsion pair
![]() $ ( \mathcal {T} , \mathcal {F} ) $
to its restriction
$ ( \mathcal {T} , \mathcal {F} ) $
to its restriction
![]() $ ( \mathcal {T} \cap \Lambda $
-
$ ( \mathcal {T} \cap \Lambda $
-
![]() $\mathrm {mod}, \mathcal {F} \cap \Lambda $
-
$\mathrm {mod}, \mathcal {F} \cap \Lambda $
-
![]() $\mathrm {mod} ) $
.
$\mathrm {mod} ) $
.
Proof. We prove that the restriction map is bijective, with inverse as above.
Let
![]() $ ( \mathcal {T} , \mathcal {F} ) $
be a torsion pair in
$ ( \mathcal {T} , \mathcal {F} ) $
be a torsion pair in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
with definable torsion class. Let
$\mathrm {Mod} $
with definable torsion class. Let
![]() $ (\mathbf {t}, \mathbf {f}) $
be the corresponding restriction.
$ (\mathbf {t}, \mathbf {f}) $
be the corresponding restriction.
We want to show that
![]() $ \mathcal {T} = {}^{\perp _0} \mathbf {f} $
. The inclusion
$ \mathcal {T} = {}^{\perp _0} \mathbf {f} $
. The inclusion
![]() $ \mathcal { T } \subseteq {}^{\perp _0} \mathbf {f} $
is immediate.
$ \mathcal { T } \subseteq {}^{\perp _0} \mathbf {f} $
is immediate.
For the opposite one, let
![]() $ M \in {}^{\perp _0} \mathbf {f} $
. By Lemma 2.15,
$ M \in {}^{\perp _0} \mathbf {f} $
. By Lemma 2.15,
![]() $ M $
can be obtained as a pure subobject of a direct product of finitely generated objects in
$ M $
can be obtained as a pure subobject of a direct product of finitely generated objects in
![]() $ {}^{\perp _0} \mathbf {f} $
which are exactly the modules in
$ {}^{\perp _0} \mathbf {f} $
which are exactly the modules in
![]() $ \mathbf {t} $
.
$ \mathbf {t} $
.
Whence
![]() $ M $
is a pure submodule of a product of objects in
$ M $
is a pure submodule of a product of objects in
![]() $ \mathcal {T} $
, so that by definability it follows that
$ \mathcal {T} $
, so that by definability it follows that
![]() $ M \in \mathcal {T} $
.
$ M \in \mathcal {T} $
.
This proves the injectivity of the restriction map. Surjectivity follows form the fact that for any torsion pair
![]() $ ( \mathbf {t}, \mathbf {f} ) $
in
$ ( \mathbf {t}, \mathbf {f} ) $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
, the torsion pair
$\mathrm {mod} $
, the torsion pair
![]() $ ({}^{\perp _0} \mathbf {f}, \mathbf {F}(\mathbf {f})) $
is an extension to
$ ({}^{\perp _0} \mathbf {f}, \mathbf {F}(\mathbf {f})) $
is an extension to
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod}$
with definable torsion class.
$\mathrm {Mod}$
with definable torsion class.
Since we have a continuous interplay between torsion pairs in the small and in the large module categories, we fix the following terminology, for a left Noetherian ring
![]() $ R $
.
$ R $
.
Definition 2.17. Let
![]() $ (\mathcal {T}, \mathcal {F}) $
be a torsion pair in
$ (\mathcal {T}, \mathcal {F}) $
be a torsion pair in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod}$
, and let
$\mathrm {Mod}$
, and let
![]() $ ( \mathbf {t},\mathbf {f}) $
be a torsion pair in
$ ( \mathbf {t},\mathbf {f}) $
be a torsion pair in
![]() $ R$
-
$ R$
-
![]() $\mathrm {mod} $
. Then
$\mathrm {mod} $
. Then
![]() $ (\mathcal {T}, \mathcal {F}) $
extends
$ (\mathcal {T}, \mathcal {F}) $
extends
![]() $ ( \mathbf {t},\mathbf {f}) $
if
$ ( \mathbf {t},\mathbf {f}) $
if
![]() $ \mathbf {t} = \mathcal {T} \cap R$
-
$ \mathbf {t} = \mathcal {T} \cap R$
-
![]() $\mathrm {mod} $
and
$\mathrm {mod} $
and
![]() $ \mathbf {f} = \mathcal {F} \cap R$
-
$ \mathbf {f} = \mathcal {F} \cap R$
-
![]() $\mathrm {mod} $
. We also say that
$\mathrm {mod} $
. We also say that
![]() $ (\mathcal {T}, \mathcal {F}) $
restricts to
$ (\mathcal {T}, \mathcal {F}) $
restricts to
![]() $ ( \mathbf {t},\mathbf {f}) $
.
$ ( \mathbf {t},\mathbf {f}) $
.
Example 2.18. For any torsion pair
![]() $ ( \mathbf {t},\mathbf {f}) $
in
$ ( \mathbf {t},\mathbf {f}) $
in
![]() $ R$
-
$ R$
-
![]() $\mathrm {mod} $
, we have the following two, not necessarily distinct, extensions to
$\mathrm {mod} $
, we have the following two, not necessarily distinct, extensions to
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
:
$\mathrm {Mod} $
:
-
(S) The extension with the largest torsion class
 $ ({}^{\perp _0}\mathbf {f}, \mathbf {F}(\mathbf {f}) ) $
.
$ ({}^{\perp _0}\mathbf {f}, \mathbf {F}(\mathbf {f}) ) $
. -
(C) The extension with the largest torsion-free class
 $ (\mathbf {T}(\mathbf {t}), \mathbf {t}^{\perp _0}) $
.
$ (\mathbf {T}(\mathbf {t}), \mathbf {t}^{\perp _0}) $
.
Over a left Noetherian ring
![]() $ R $
, definable torsion classes in
$ R $
, definable torsion classes in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
are parametrized by silting modules [Reference Angeleri Hügel and Hrbek3, Cor. 3.8].
$\mathrm {Mod} $
are parametrized by silting modules [Reference Angeleri Hügel and Hrbek3, Cor. 3.8].
Moreover, definable torsion-free classes over an arbitrary ring are parametrized by cosilting modules (see [Reference Breaz and Pop10], [Reference Wei and Zhang30]).
In the following sections, we always work with left Noetherian rings; therefore, we write
![]() $ \mathcal {T} \in \mathbf {Silt}(R) $
(resp.
$ \mathcal {T} \in \mathbf {Silt}(R) $
(resp.
![]() $\mathcal {F} \in \mathbf {Cosilt}(R) $
) to indicate that
$\mathcal {F} \in \mathbf {Cosilt}(R) $
) to indicate that
![]() $ \mathcal {T} $
is a definable torsion class (resp.
$ \mathcal {T} $
is a definable torsion class (resp.
![]() $ \mathcal {F} $
is a definable torsion-free class) in
$ \mathcal {F} $
is a definable torsion-free class) in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
.
$\mathrm {Mod} $
.
3 Torsion-free, almost torsion modules
The concept of torsion-free, almost torsion modules was already being used by Herzog in 2009, as a tool for studying critical summands of cotilting modules.
More recently, Barnard, Carroll, and Zhu introduced the related concept of minimal extending modules in their work on the lattice of torsion classes of the category
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
.
$\mathrm {mod} $
.
In this section,
![]() $ R $
is a left Noetherian ring.
$ R $
is a left Noetherian ring.
Definition 3.1 [Reference Barnard, Carroll and Zhu8], [Reference Herzog19].
Let
![]() $ (\mathcal { T }, \mathcal {F} ) $
be a torsion pair in
$ (\mathcal { T }, \mathcal {F} ) $
be a torsion pair in
![]() $ R$
-Mod (resp. in R-mod). Let
$ R$
-Mod (resp. in R-mod). Let
![]() $ B \ne 0 $
be a (finitely generated)
$ B \ne 0 $
be a (finitely generated)
![]() $ R $
-module. We say that
$ R $
-module. We say that
![]() $ B $
is torsion-free, almost torsion (resp. minimal extending) if:
$ B $
is torsion-free, almost torsion (resp. minimal extending) if:
-
(1)
 $ B \in \mathcal {F} $
.
$ B \in \mathcal {F} $
. -
(2) Every proper quotient of
 $ B $
is contained in
$ B $
is contained in
 $ \mathcal { T } $
.
$ \mathcal { T } $
. -
(3) For every short exact sequence
 $ 0 \to B \to F \to M \to 0 $
, if
$ 0 \to B \to F \to M \to 0 $
, if
 $ F \in \mathcal {F} $
, then
$ F \in \mathcal {F} $
, then
 $ M \in \mathcal {F} $
.
$ M \in \mathcal {F} $
.
Condition (2) is equivalent to:
-
(2’) For any
 $ F \in \mathcal {F} $
, any nonzero morphism
$ F \in \mathcal {F} $
, any nonzero morphism
 $ B \to F $
is a monomorphism
$ B \to F $
is a monomorphism
Moreover, assuming conditions (1) and (2), we have the following reformulation of (3):
-
(3’) For every nonsplit short exact sequence
 $ 0 \to B \to M \to T \to 0 $
, if
$ 0 \to B \to M \to T \to 0 $
, if
 $ T \in \mathcal { T } $
, then
$ T \in \mathcal { T } $
, then
 $ M \in \mathcal { T } $
.
$ M \in \mathcal { T } $
.
Dually, we can define torsion, almost torsion-free (and minimal co-extending) modules.
Remark 3.2. Modules satisfying conditions (1) and (2) in the definition above are precisely the simple torsion-free objects used in Enomoto’s study of torsion-free classes [Reference Enomoto16].
Lemma 3.3. For a module satisfying (1) and (2), condition (3) is equivalent to condition (3’).
Proof. Fix a module
![]() $ B \ne 0 $
satisfying (1) and (2) with respect to some torsion pair
$ B \ne 0 $
satisfying (1) and (2) with respect to some torsion pair
![]() $ ( \mathcal { T }, \mathcal { F } ) $
.
$ ( \mathcal { T }, \mathcal { F } ) $
.
![]() $"(3) \implies (3')":$
Assume that
$"(3) \implies (3')":$
Assume that
![]() $ B $
satisfies condition (3). Consider a short exact sequence
$ B $
satisfies condition (3). Consider a short exact sequence
![]() $ 0 \to B \to M \to T \to 0 $
, with
$ 0 \to B \to M \to T \to 0 $
, with
![]() $ T $
torsion.
$ T $
torsion.
Take the canonical short exact sequence given by the torsion pair
with
![]() $ tM $
torsion,
$ tM $
torsion,
![]() $ M/tM $
torsion-free.
$ M/tM $
torsion-free.
Since
![]() $ B $
satisfies (2), the map
$ B $
satisfies (2), the map
![]() $ g : B \to M \to M/tM $
is zero or injective. Assume that it is zero. Then we have the following commutative diagram, by the snake lemma and the universal property of the kernel:
$ g : B \to M \to M/tM $
is zero or injective. Assume that it is zero. Then we have the following commutative diagram, by the snake lemma and the universal property of the kernel:

Since
![]() $ T $
is torsion, the map
$ T $
is torsion, the map
![]() $ T \to M' $
must be zero; therefore,
$ T \to M' $
must be zero; therefore,
![]() $ M/tM = 0 $
and
$ M/tM = 0 $
and
![]() $ M $
is torsion.
$ M $
is torsion.
Assume now that
![]() $ g $
is injective. Consider the following commutative diagram:
$ g $
is injective. Consider the following commutative diagram:

By (3), the module
![]() $ M' $
is both torsion and torsion-free; therefore,
$ M' $
is both torsion and torsion-free; therefore,
![]() $ M' = 0 $
and the sequence
$ M' = 0 $
and the sequence
![]() $ 0 \to B \to M \to T \to 0 $
is split. In conclusion,
$ 0 \to B \to M \to T \to 0 $
is split. In conclusion,
![]() $ B $
satisfies (3’).
$ B $
satisfies (3’).
![]() $"(3') \implies (3)":$
Assume now that
$"(3') \implies (3)":$
Assume now that
![]() $ B $
satisfies (3’). Take a short exact sequence
$ B $
satisfies (3’). Take a short exact sequence
![]() $ 0 \to B \to F \to M \to 0 $
, with
$ 0 \to B \to F \to M \to 0 $
, with
![]() $ F $
torsion-free. Consider the torsion, torsion-free sequence for
$ F $
torsion-free. Consider the torsion, torsion-free sequence for
![]() $ M $
as above and take the pullback to obtain the commutative diagram:
$ M $
as above and take the pullback to obtain the commutative diagram:

Since
![]() $ M' $
is a submodule of
$ M' $
is a submodule of
![]() $ F $
, it is torsion-free. Now, applying the contrapositive of (3’), it follows that the sequence
$ F $
, it is torsion-free. Now, applying the contrapositive of (3’), it follows that the sequence
![]() $ 0 \to B \to M' \to tM \to 0 $
splits, whence
$ 0 \to B \to M' \to tM \to 0 $
splits, whence
![]() $ tM = 0 $
and
$ tM = 0 $
and
![]() $ M $
is torsion-free.
$ M $
is torsion-free.
3.1 Simples in the heart
Torsion-free, almost torsion modules for any torsion pair
![]() $ (\mathcal {T},\mathcal {F}) $
enjoy several orthogonality properties: these follow at once from their characterization as simple objects in a suitable abelian subcategory of
$ (\mathcal {T},\mathcal {F}) $
enjoy several orthogonality properties: these follow at once from their characterization as simple objects in a suitable abelian subcategory of
![]() $ D(R) $
.
$ D(R) $
.
This subcategory is the heart of the t-structure obtained from
![]() $ (\mathcal {T},\mathcal {F}) $
by the Happel–Reiten–Smalø construction [Reference Happel, Reiten and Smalø18, I.2], which we recall below.
$ (\mathcal {T},\mathcal {F}) $
by the Happel–Reiten–Smalø construction [Reference Happel, Reiten and Smalø18, I.2], which we recall below.
For a classical reference on derived categories and t-structures, see [Reference Gelfand and Manin17].
Definition 3.4. Let
![]() $ \mathcal {T} $
be a triangulated category with shift functor
$ \mathcal {T} $
be a triangulated category with shift functor
![]() $ \Sigma $
. A t-structure in
$ \Sigma $
. A t-structure in
![]() $ \mathcal {T} $
consists of a pair
$ \mathcal {T} $
consists of a pair
![]() $ ( \mathcal {U}, \mathcal {V} ) $
of full subcategories closed under isomorphism such that:
$ ( \mathcal {U}, \mathcal {V} ) $
of full subcategories closed under isomorphism such that:
-
(i)
 $ \mathrm {Hom}_{\mathcal {T}}(U, V) = 0 $
for all
$ \mathrm {Hom}_{\mathcal {T}}(U, V) = 0 $
for all
 $ U \in \mathcal {U} $
,
$ U \in \mathcal {U} $
,
 $ V \in \mathcal {V} $
.
$ V \in \mathcal {V} $
. -
(ii)
 $ \Sigma \mathcal {U} \subseteq \mathcal {U} $
.
$ \Sigma \mathcal {U} \subseteq \mathcal {U} $
. -
(iii) For every object
 $ T \in \mathcal {T} $
, there exists a triangle: with
$ T \in \mathcal {T} $
, there exists a triangle: with $$\begin{align*}U \to T \to V \to \Sigma U \end{align*}$$
$$\begin{align*}U \to T \to V \to \Sigma U \end{align*}$$
 $ U \in \mathcal { U } $
and
$ U \in \mathcal { U } $
and
 $ V \in \mathcal {V} $
.
$ V \in \mathcal {V} $
.
Proposition 3.5 [Reference Happel, Reiten and Smalø18, I.2].
Let
![]() $ \mathfrak {t} = (\mathcal {T}, \mathcal { F }) $
be a torsion pair in a Grothendieck category
$ \mathfrak {t} = (\mathcal {T}, \mathcal { F }) $
be a torsion pair in a Grothendieck category
![]() $ \mathcal {G} $
. The classes
$ \mathcal {G} $
. The classes
 $$ \begin{align*} \mathcal{D}_{\mathfrak{t}}^{\le -1} = & \left\lbrace X^\bullet \in \mathcal{D}(\mathcal{G})\ |\ H^0(X^\bullet) \in \mathcal{T},\ H^i(X^\bullet) = 0,\ \text{for all}\ i> 0 \right\rbrace, \\ \mathcal{D}_{\mathfrak{t}}^{\ge 0} = & \left\lbrace X^\bullet \in \mathcal{D}(\mathcal{G}) \ |\ H^{0}(X^\bullet) \in \mathcal{F},\ H^i(X^\bullet) = 0,\ \text{for all}\ i < 0 \right\rbrace \end{align*} $$
$$ \begin{align*} \mathcal{D}_{\mathfrak{t}}^{\le -1} = & \left\lbrace X^\bullet \in \mathcal{D}(\mathcal{G})\ |\ H^0(X^\bullet) \in \mathcal{T},\ H^i(X^\bullet) = 0,\ \text{for all}\ i> 0 \right\rbrace, \\ \mathcal{D}_{\mathfrak{t}}^{\ge 0} = & \left\lbrace X^\bullet \in \mathcal{D}(\mathcal{G}) \ |\ H^{0}(X^\bullet) \in \mathcal{F},\ H^i(X^\bullet) = 0,\ \text{for all}\ i < 0 \right\rbrace \end{align*} $$
form a t-structure
![]() $ (\mathcal {D}_{\mathfrak {t}}^{\le -1}, \mathcal {D}_{\mathfrak {t}}^{\ge 0} ) $
in
$ (\mathcal {D}_{\mathfrak {t}}^{\le -1}, \mathcal {D}_{\mathfrak {t}}^{\ge 0} ) $
in
![]() $ D(\mathcal {G}) $
. We denote the corresponding heart by
$ D(\mathcal {G}) $
. We denote the corresponding heart by
![]() $ \mathscr {H}_{\mathfrak {t}} = \mathcal {D}_{\mathfrak {t}}^{\le -1}[-1] \cap \mathcal {D}_{\mathfrak {t}}^{\ge 0} $
.
$ \mathscr {H}_{\mathfrak {t}} = \mathcal {D}_{\mathfrak {t}}^{\le -1}[-1] \cap \mathcal {D}_{\mathfrak {t}}^{\ge 0} $
.
The t-structure obtained by choosing the trivial torsion pair
![]() $ (0, \mathcal {G} ) $
is the standard t-structure
$ (0, \mathcal {G} ) $
is the standard t-structure
![]() $ (\mathcal {D}^{\le -1}, \mathcal {D}^{\ge 0} ) $
with heart
$ (\mathcal {D}^{\le -1}, \mathcal {D}^{\ge 0} ) $
with heart
![]() $ \mathcal {G} $
.
$ \mathcal {G} $
.
Remark 3.6. Recall that the heart of a t-structure is always an abelian category. (An accessible proof can be found in [Reference Miličić20, Sec. 1.2].)
Moreover, the torsion pair
![]() $ \mathfrak {t} = (\mathcal {T}, \mathcal {F}) $
in the category
$ \mathfrak {t} = (\mathcal {T}, \mathcal {F}) $
in the category
![]() $ R$
-Mod induces a torsion pair
$ R$
-Mod induces a torsion pair
![]() $ (\mathcal {F}, \mathcal {T}[-1]) $
in the corresponding heart
$ (\mathcal {F}, \mathcal {T}[-1]) $
in the corresponding heart
![]() $ \mathscr {H}_{\mathfrak {t}} $
.
$ \mathscr {H}_{\mathfrak {t}} $
.
In fact,
![]() $\mathrm {Hom}(\mathcal {F},\mathcal {T}[-1]) = 0 $
, as modules do not have any extension in negative degrees, and for every object
$\mathrm {Hom}(\mathcal {F},\mathcal {T}[-1]) = 0 $
, as modules do not have any extension in negative degrees, and for every object
![]() $ H $
of the heart, we can construct an approximation triangle in
$ H $
of the heart, we can construct an approximation triangle in
![]() $ \mathcal {D}(R) $
with respect to the standard t-structure
$ \mathcal {D}(R) $
with respect to the standard t-structure
![]() $ (\mathcal {D}^{\le -1}, \mathcal {D}^{\ge 0} ) $
. This induces a short exact sequence
$ (\mathcal {D}^{\le -1}, \mathcal {D}^{\ge 0} ) $
. This induces a short exact sequence
with
![]() $ H^0(H) \in \mathcal {F} $
and
$ H^0(H) \in \mathcal {F} $
and
![]() $ H^{1}(H) \in \mathcal {T} $
as required.
$ H^{1}(H) \in \mathcal {T} $
as required.
Theorem 3.7 [Reference Angeleri Hügel, Herzog and Laking2].
Let
![]() $ \mathfrak {t} = (\mathcal {T},\mathcal {F} ) $
be a torsion pair in
$ \mathfrak {t} = (\mathcal {T},\mathcal {F} ) $
be a torsion pair in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
. The simple objects in the HRS-heart
$\mathrm {Mod} $
. The simple objects in the HRS-heart
![]() $\mathscr {H}_{\mathfrak {t}}$
are precisely the objects
$\mathscr {H}_{\mathfrak {t}}$
are precisely the objects
![]() $ S $
of the form
$ S $
of the form
![]() $ S = F $
with
$ S = F $
with
![]() $ F $
torsion-free, almost torsion, or
$ F $
torsion-free, almost torsion, or
![]() $ S = T[-1] $
with
$ S = T[-1] $
with
![]() $ T $
torsion, almost torsion-free.
$ T $
torsion, almost torsion-free.
For a proof of the result above, see [Reference Rapa25, Th. 2.3.6].
Corollary 3.8. The collection of torsion-free, almost torsion objects for any torsion pair in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
is a semibrick, that is, a set of pairwise orthogonal modules whose endomorphism ring is a division ring. The same holds for torsion, almost torsion-free modules.
$\mathrm {Mod} $
is a semibrick, that is, a set of pairwise orthogonal modules whose endomorphism ring is a division ring. The same holds for torsion, almost torsion-free modules.
We may also obtain some further orthogonality properties of torsion-free, almost torsion and torsion, almost torsion-free modules.
Corollary 3.9. Let
![]() $ (\mathcal { T }, \mathcal { F }) $
be a torsion pair in
$ (\mathcal { T }, \mathcal { F }) $
be a torsion pair in
![]() $ R$
-
$ R$
-
![]() $\mathrm {Mod} $
. Let
$\mathrm {Mod} $
. Let
![]() $ \mathcal {S} $
be the collection of all the torsion, almost torsion-free modules with respect to this pair.
$ \mathcal {S} $
be the collection of all the torsion, almost torsion-free modules with respect to this pair.
Then any torsion-free, almost torsion module is contained in
![]() $ \mathcal {S}^{\perp _1} \cap \mathcal {F} $
.
$ \mathcal {S}^{\perp _1} \cap \mathcal {F} $
.
We end this section by recalling the following result of Parra and Saorín [Reference Parra and Saorín21], [Reference Parra and Saorín22] which we will use later.
Theorem 3.10. Let
![]() $ \mathcal {G} $
be a Grothendieck category, and let
$ \mathcal {G} $
be a Grothendieck category, and let
![]() $ (\mathcal {T}, \mathcal {F} ) $
be a torsion pair in
$ (\mathcal {T}, \mathcal {F} ) $
be a torsion pair in
![]() $ \mathcal {G} $
. Then the heart associated with the HRS-tilt at
$ \mathcal {G} $
. Then the heart associated with the HRS-tilt at
![]() $ (\mathcal {T}, \mathcal {F} ) $
is Grothendieck if and only if
$ (\mathcal {T}, \mathcal {F} ) $
is Grothendieck if and only if
![]() $ \mathcal {F} $
is definable.
$ \mathcal {F} $
is definable.
3.2 The small and the large ones
Since the definition of minimal extending modules for a torsion pair in
![]() $ R$
-mod is identical to the definition of torsion-free, almost torsion modules for torsion pairs in R-Mod, we rightfully expect to have a relation between the two notions.
$ R$
-mod is identical to the definition of torsion-free, almost torsion modules for torsion pairs in R-Mod, we rightfully expect to have a relation between the two notions.
This is indeed the case:
Proposition 3.11. Let
![]() $ R $
be a left Noetherian ring. Let
$ R $
be a left Noetherian ring. Let
![]() $ (\mathbf { t }, \mathbf { f }) $
be a torsion pair in
$ (\mathbf { t }, \mathbf { f }) $
be a torsion pair in
![]() $ R$
-mod, and let
$ R$
-mod, and let
![]() $ ( \mathcal {T} = \underrightarrow {\lim }\, \mathbf { t }, \mathcal {F} = \underrightarrow {\lim }\, \mathbf { f } ) $
be the corresponding torsion pair in
$ ( \mathcal {T} = \underrightarrow {\lim }\, \mathbf { t }, \mathcal {F} = \underrightarrow {\lim }\, \mathbf { f } ) $
be the corresponding torsion pair in
![]() $ R$
-Mod with definable torsion-free class (with respect to the bijection in Theorem 2.14).
$ R$
-Mod with definable torsion-free class (with respect to the bijection in Theorem 2.14).
Then the minimal extending modules with respect to
![]() $ (\mathbf { t }, \mathbf { f }) $
are precisely the finitely generated torsion-free, almost torsion modules for
$ (\mathbf { t }, \mathbf { f }) $
are precisely the finitely generated torsion-free, almost torsion modules for
![]() $ (\mathcal {T}, \mathcal {F}) $
.
$ (\mathcal {T}, \mathcal {F}) $
.
Moreover, all torsion, almost torsion-free modules for
![]() $ (\mathcal {T}, \mathcal {F}) $
are finitely generated and coincide with the minimal co-extending modules for
$ (\mathcal {T}, \mathcal {F}) $
are finitely generated and coincide with the minimal co-extending modules for
![]() $ (\mathbf { t }, \mathbf { f }) $
.
$ (\mathbf { t }, \mathbf { f }) $
.
We need the following lemma in the proof.
Lemma 3.12. Let
![]() $ (\mathcal { T }, \mathcal { F }) $
be a torsion pair with
$ (\mathcal { T }, \mathcal { F }) $
be a torsion pair with
![]() $ \mathcal {F} \in \mathbf {Cosilt}(R) $
. Then all the torsion, almost torsion-free modules are finitely generated.
$ \mathcal {F} \in \mathbf {Cosilt}(R) $
. Then all the torsion, almost torsion-free modules are finitely generated.
Over a finite-dimensional algebra
![]() $\Lambda $
, we can say dually that for a torsion class in
$\Lambda $
, we can say dually that for a torsion class in
![]() $ \mathbf {Silt}(\Lambda ) $
all torsion-free, almost torsion modules are finite-dimensional.
$ \mathbf {Silt}(\Lambda ) $
all torsion-free, almost torsion modules are finite-dimensional.
Proof. By Theorem 2.14, the torsion pair can be written as
![]() $ ( \mathrm {Gen}(\mathbf {t}) , \mathbf {t}^{\perp _0} ) $
with
$ ( \mathrm {Gen}(\mathbf {t}) , \mathbf {t}^{\perp _0} ) $
with
![]() $ \mathbf {t} $
torsion class in
$ \mathbf {t} $
torsion class in
![]() $ R$
-mod.
$ R$
-mod.
Assume that
![]() $ T $
is torsion, almost torsion-free and
$ T $
is torsion, almost torsion-free and
![]() $ T \not \in R$
-
$ T \not \in R$
-
![]() $\mathrm {mod}$
. By assumption, all proper submodules of
$\mathrm {mod}$
. By assumption, all proper submodules of
![]() $ T $
, in particular all possible images of morphisms from a finitely generated module, must be torsion-free, whence
$ T $
, in particular all possible images of morphisms from a finitely generated module, must be torsion-free, whence
![]() $ T \in \mathbf { t }^{ \perp _0 } $
. This yields a contradiction.
$ T \in \mathbf { t }^{ \perp _0 } $
. This yields a contradiction.
For the second case, proceed dually using Theorem 2.16.
Now, we can prove the proposition.
Proof. It is clear that the finitely generated torsion-free, almost torsion modules for
![]() $ (\mathcal {T}, \mathcal {F}) $
are minimal extending for
$ (\mathcal {T}, \mathcal {F}) $
are minimal extending for
![]() $ (\mathbf { t }, \mathbf { f }) $
.
$ (\mathbf { t }, \mathbf { f }) $
.
So suppose that
![]() $ S $
is minimal extending. We have immediately
$ S $
is minimal extending. We have immediately
![]() $ S \in \mathcal {F} $
and that all its proper quotients are in
$ S \in \mathcal {F} $
and that all its proper quotients are in
![]() $ \mathbf { t } $
, so in particular in
$ \mathbf { t } $
, so in particular in
![]() $ \mathcal {T} $
.
$ \mathcal {T} $
.
The only condition that we have to check is the last one: consider a short exact sequence
with
![]() $ F \in \mathcal { F } $
. Recall that
$ F \in \mathcal { F } $
. Recall that
![]() $ \mathcal { F } = \mathbf { t }^{\perp _0} $
. Hence, suppose that we have a map
$ \mathcal { F } = \mathbf { t }^{\perp _0} $
. Hence, suppose that we have a map
![]() $ T \to M $
with
$ T \to M $
with
![]() $ T \in \mathbf { t } $
which we may assume, without loss of generality, to be injective; taking the pullback, we obtain the commutative diagram:
$ T \in \mathbf { t } $
which we may assume, without loss of generality, to be injective; taking the pullback, we obtain the commutative diagram:

whose first row is in
![]() $ R$
-mod. Applying the minimal extending property (3’) of
$ R$
-mod. Applying the minimal extending property (3’) of
![]() $ S $
to
$ S $
to
![]() $ 0 \to S \to P \to T \to 0 $
, we obtain that either
$ 0 \to S \to P \to T \to 0 $
, we obtain that either
![]() $ P $
is torsion or the sequence splits. Since
$ P $
is torsion or the sequence splits. Since
![]() $ P $
is a submodule of
$ P $
is a submodule of
![]() $ F $
, it must be torsion-free, so the sequence splits, and
$ F $
, it must be torsion-free, so the sequence splits, and
![]() $ T = 0 $
, proving that
$ T = 0 $
, proving that
![]() $ M \in \mathbf { t }^{\perp _0} $
.
$ M \in \mathbf { t }^{\perp _0} $
.
The proof of the second statement is more involved, as the available description of
![]() $ \mathcal {T} $
is less practical to work with.
$ \mathcal {T} $
is less practical to work with.
We need to check that every minimal co-extending module is torsion, almost torsion-free. Let
![]() $ S $
be minimal co-extending. By definition,
$ S $
be minimal co-extending. By definition,
![]() $ S \in \mathbf {t} \subseteq \mathcal {T} $
.
$ S \in \mathbf {t} \subseteq \mathcal {T} $
.
The second property is immediately verified, as every proper submodule of
![]() $ S $
is an element of
$ S $
is an element of
![]() $ \mathbf {f} \subseteq \mathcal {F} $
.
$ \mathbf {f} \subseteq \mathcal {F} $
.
For the third property, consider a short exact sequence
with
![]() $ T \in \mathcal { T } $
. By Theorem 2.14, we can find a family
$ T \in \mathcal { T } $
. By Theorem 2.14, we can find a family
![]() $ \{U_i\}_{i \in I} $
of objects of
$ \{U_i\}_{i \in I} $
of objects of
![]() $ \mathbf {t} $
, with an epimorphism
$ \mathbf {t} $
, with an epimorphism
![]() $ h : \coprod _I U_i \to T $
.
$ h : \coprod _I U_i \to T $
.
Since
![]() $ S $
is finitely generated, we can find a finite subset
$ S $
is finitely generated, we can find a finite subset
![]() $ I_0 \subseteq I $
such that
$ I_0 \subseteq I $
such that
![]() $ \tilde {f} = f \circ h \circ \iota _{I_0} $
is surjective (where
$ \tilde {f} = f \circ h \circ \iota _{I_0} $
is surjective (where
![]() $ \iota _{I_0} : \coprod _{I_0} U_i \to \coprod _I U_i $
).
$ \iota _{I_0} : \coprod _{I_0} U_i \to \coprod _I U_i $
).
By definition,
![]() $ \coprod _{I_0} U_i \in \mathbf {t} $
, whence
$ \coprod _{I_0} U_i \in \mathbf {t} $
, whence
![]() $ K' = \ker \tilde {f} $
is a torsion module, as
$ K' = \ker \tilde {f} $
is a torsion module, as
![]() $ S $
is minimal co-extending.
$ S $
is minimal co-extending.
Consider the following pullback diagram:

Notice that
![]() $ P \in \mathcal { T } $
since
$ P \in \mathcal { T } $
since
![]() $ T $
and
$ T $
and
![]() $ K' $
are torsion modules.
$ K' $
are torsion modules.
Then consider the map
![]() $ h \circ \iota _{I_0} : \coprod _{I_0} U_i \to T $
. Using the universal property of the pullback, we obtain the following commutative diagram:
$ h \circ \iota _{I_0} : \coprod _{I_0} U_i \to T $
. Using the universal property of the pullback, we obtain the following commutative diagram:

Thus, the middle horizontal short exact sequence in the first diagram splits, and hence
![]() $ K \in \mathcal { T } $
.
$ K \in \mathcal { T } $
.
3.3 Torsion-free, almost torsion, and functorially finite classes
Starting from this section, we always work over a finite-dimensional algebra
![]() $ \Lambda $
.
$ \Lambda $
.
For a torsion pair
![]() $ (\mathbf {t}, \mathbf {f} ) $
in
$ (\mathbf {t}, \mathbf {f} ) $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod}, $
we know by work of Smalø [Reference Smalø28] that
$\mathrm {mod}, $
we know by work of Smalø [Reference Smalø28] that
![]() $ \mathbf {t} $
is functorially finite if and only if
$ \mathbf {t} $
is functorially finite if and only if
![]() $ \mathbf {f} $
is functorially finite (see Definition 2.4).
$ \mathbf {f} $
is functorially finite (see Definition 2.4).
Functorially finite torsion pairs are parametrized by support
![]() $ \tau $
-tilting modules.
$ \tau $
-tilting modules.
Theorem 3.13 [Reference Adachi, Iyama and Reiten1, Th. 2.7].
There is a bijection between functorially finite torsion classes in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
and equivalence classes of support
$\mathrm {mod} $
and equivalence classes of support
![]() $ \tau $
-tilting
$ \tau $
-tilting
![]() $ \Lambda $
-modules, which associates to any representative
$ \Lambda $
-modules, which associates to any representative
![]() $ T $
the torsion class
$ T $
the torsion class
![]() $ \widetilde {\mathbf {T}}(T) = \mathrm {gen}(T) $
.
$ \widetilde {\mathbf {T}}(T) = \mathrm {gen}(T) $
.
Such classes admit a unique extension to
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
as was already observed in [Reference Vitória29]. We give a proof for completeness.
$\mathrm {Mod} $
as was already observed in [Reference Vitória29]. We give a proof for completeness.
Proposition 3.14 [Reference Vitória29, Prop. 5.3].
Let
![]() $ (\mathbf {t}, \mathbf {f} ) $
be a torsion pair in
$ (\mathbf {t}, \mathbf {f} ) $
be a torsion pair in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod}$
. Then the following statements are equivalent:
$\mathrm {mod}$
. Then the following statements are equivalent:
-
(1)
 $ \mathbf {t} $
is functorially finite.
$ \mathbf {t} $
is functorially finite. -
(2) There exists a torsion pair
 $ ( \mathcal { T }, \mathcal { F }) $
in
$ ( \mathcal { T }, \mathcal { F }) $
in
 $ \Lambda $
-
$ \Lambda $
-
 $\mathrm {Mod}$
extending
$\mathrm {Mod}$
extending
 $( \mathbf {t}, \mathbf {f} )$
, such that both the torsion and the torsion-free classes are definable.
$( \mathbf {t}, \mathbf {f} )$
, such that both the torsion and the torsion-free classes are definable. -
(3) There is a unique torsion pair extending
 $ ( \mathbf {t} , \mathbf {f} ) $
to
$ ( \mathbf {t} , \mathbf {f} ) $
to
 $ \Lambda $
-Mod.
$ \Lambda $
-Mod.
Proof. “(1)
![]() $\implies $
(2)”: By Theorem 3.13, we find a support
$\implies $
(2)”: By Theorem 3.13, we find a support
![]() $ \tau $
-tilting module
$ \tau $
-tilting module
![]() $ T $
generating
$ T $
generating
![]() $ \mathbf {t} $
. The torsion pair
$ \mathbf {t} $
. The torsion pair
![]() $ ( \mathbf {T}(T), T^{\perp _0} ) $
in
$ ( \mathbf {T}(T), T^{\perp _0} ) $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
extends the original torsion pair and it is definable on both sides:
$\mathrm {Mod} $
extends the original torsion pair and it is definable on both sides:
![]() $ \mathbf {T}(T) = \mathrm {Gen}(\mathrm {gen}(T)) = \mathrm {Gen}(T) = \underrightarrow {\lim } (\mathrm {gen}(T) ) $
by Theorem 2.14. To obtain definability of the last torsion class, we can apply a result of Lenzing (see [Reference Prest24, Cor. 3.4.37]), since
$ \mathbf {T}(T) = \mathrm {Gen}(\mathrm {gen}(T)) = \mathrm {Gen}(T) = \underrightarrow {\lim } (\mathrm {gen}(T) ) $
by Theorem 2.14. To obtain definability of the last torsion class, we can apply a result of Lenzing (see [Reference Prest24, Cor. 3.4.37]), since
![]() $ \mathrm {gen}(T) $
is functorially finite.
$ \mathrm {gen}(T) $
is functorially finite.
“(2)
![]() $\implies $
(1)”: By assumption, we have a torsion pair
$\implies $
(1)”: By assumption, we have a torsion pair
![]() $ ( \mathcal { T }, \mathcal { F }) $
extending
$ ( \mathcal { T }, \mathcal { F }) $
extending
![]() $ (\mathbf {t}, \mathbf {f} ) $
to
$ (\mathbf {t}, \mathbf {f} ) $
to
![]() $ \Lambda $
-Mod, such that both the torsion and the torsion-free classes are definable. Using Theorem 2.14, we obtain that
$ \Lambda $
-Mod, such that both the torsion and the torsion-free classes are definable. Using Theorem 2.14, we obtain that
![]() $ \mathcal { T } = \underrightarrow {\lim }(\mathbf {t} ) $
.
$ \mathcal { T } = \underrightarrow {\lim }(\mathbf {t} ) $
.
Then we can apply [Reference Prest24, Cor. 3.4.37], ensuring that the torsion class
![]() $ \mathbf { t } $
has left approximations, and hence it is functorially finite. (Every torsion class provides right approximations.)
$ \mathbf { t } $
has left approximations, and hence it is functorially finite. (Every torsion class provides right approximations.)
“(2)
![]() $ \implies $
(3)”: Using Theorems 2.14 and 2.16, it follows that
$ \implies $
(3)”: Using Theorems 2.14 and 2.16, it follows that
![]() $ \mathcal {T} = {}^{\perp _0}\mathbf {f} $
and
$ \mathcal {T} = {}^{\perp _0}\mathbf {f} $
and
![]() $ \mathcal {F} = \mathbf {t}^{\perp _0} $
. Let
$ \mathcal {F} = \mathbf {t}^{\perp _0} $
. Let
![]() $ (\mathcal {U}, \mathcal {V} ) $
be a torsion pair in
$ (\mathcal {U}, \mathcal {V} ) $
be a torsion pair in
![]() $ \Lambda $
-Mod extending
$ \Lambda $
-Mod extending
![]() $ (\mathbf {t}, \mathbf {f}) $
. Then we have
$ (\mathbf {t}, \mathbf {f}) $
. Then we have
![]() $ \mathcal {V} = \mathcal {U}^{\perp _0} \subseteq \mathbf {t}^{\perp _0} $
and
$ \mathcal {V} = \mathcal {U}^{\perp _0} \subseteq \mathbf {t}^{\perp _0} $
and
![]() $ \mathcal {U} = {}^{\perp _0} \mathcal {V} \subseteq {}^{\perp _0} \mathbf {f} $
. From this, we deduce that
$ \mathcal {U} = {}^{\perp _0} \mathcal {V} \subseteq {}^{\perp _0} \mathbf {f} $
. From this, we deduce that
![]() $ \mathcal {V} = \mathcal {U}^{\perp _0} = ({}^{\perp _0}\mathcal {V})^{\perp _0} \supseteq ({}^{\perp _0}\mathbf {f})^{\perp _0} = \mathcal {F} $
. In conclusion,
$ \mathcal {V} = \mathcal {U}^{\perp _0} = ({}^{\perp _0}\mathcal {V})^{\perp _0} \supseteq ({}^{\perp _0}\mathbf {f})^{\perp _0} = \mathcal {F} $
. In conclusion,
![]() $ \mathcal {V} = \mathcal {F} $
, proving that there is a unique extension.
$ \mathcal {V} = \mathcal {F} $
, proving that there is a unique extension.
“(3)
![]() $ \implies $
(2)”: Immediate, using the fact that the extension with definable torsion class and the one with definable torsion-free class must coincide.
$ \implies $
(2)”: Immediate, using the fact that the extension with definable torsion class and the one with definable torsion-free class must coincide.
Corollary 3.15. Let
![]() $ (\mathbf {t}, \mathbf {f}) $
be a functorially finite torsion pair in
$ (\mathbf {t}, \mathbf {f}) $
be a functorially finite torsion pair in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
.
$\mathrm {mod} $
.
Then, for its unique extension
![]() $ ( \mathcal {T}, \mathcal {F}) $
to
$ ( \mathcal {T}, \mathcal {F}) $
to
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
, all the torsion-free, almost torsion and torsion, almost torsion-free modules are finite-dimensional.
$\mathrm {Mod} $
, all the torsion-free, almost torsion and torsion, almost torsion-free modules are finite-dimensional.
3.4 Torsion-free, almost torsion modules determine torsion pairs
We want to prove that a definable torsion-free class
![]() $ \mathcal {F} $
in
$ \mathcal {F} $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
is uniquely determined by its torsion-free, almost torsion modules.
$\mathrm {Mod} $
is uniquely determined by its torsion-free, almost torsion modules.
This is a consequence of the following lemma, ensuring the existence of finitely generated, even finitely presented, objects in the heart associated with
![]() $ \mathcal {F} $
and of the characterization of torsion-free, almost torsion modules as simple objects in the heart.
$ \mathcal {F} $
and of the characterization of torsion-free, almost torsion modules as simple objects in the heart.
Lemma 3.16 [Reference Parra, Saorín and Virili23, Cor. 4.3].
Any finite-dimensional module in
![]() $ \mathcal { F} $
is finitely presented when seen as an object in the heart
$ \mathcal { F} $
is finitely presented when seen as an object in the heart
![]() $ \mathscr {H} $
of the associated HRS t-structure.
$ \mathscr {H} $
of the associated HRS t-structure.
Remark 3.17. The original result in [Reference Parra, Saorín and Virili23] is much stronger and gives a complete description of finitely presented objects in the torsion class
![]() $ \mathcal {F} $
in
$ \mathcal {F} $
in
![]() $ \mathscr {H} $
in terms of properties of the corresponding modules.
$ \mathscr {H} $
in terms of properties of the corresponding modules.
At this point, we can prove the following corollary.
Corollary 3.18. Consider a definable torsion-free class
![]() $ 0 \ne \mathcal {F} \in \mathbf {Cosilt}(\Lambda ) $
, then there exists some (not necessarily finite-dimensional) torsion-free, almost torsion module.
$ 0 \ne \mathcal {F} \in \mathbf {Cosilt}(\Lambda ) $
, then there exists some (not necessarily finite-dimensional) torsion-free, almost torsion module.
Proof. Since
![]() $ 0 \ne \mathcal {F} $
, by Theorem 2.14, there exists some nonzero finite-dimensional module
$ 0 \ne \mathcal {F} $
, by Theorem 2.14, there exists some nonzero finite-dimensional module
![]() $ F \in \mathcal {F} $
.
$ F \in \mathcal {F} $
.
![]() $ F $
is a nonzero finitely generated object in
$ F $
is a nonzero finitely generated object in
![]() $ \mathscr {H} $
, which is a Grothendieck category by Theorem 3.10, whence
$ \mathscr {H} $
, which is a Grothendieck category by Theorem 3.10, whence
![]() $ F $
has a maximal subobject, giving rise to a simple quotient
$ F $
has a maximal subobject, giving rise to a simple quotient
![]() $ S $
which is an element of
$ S $
which is an element of
![]() $ \mathcal { F } $
, as this is a torsion class in the heart (see Remark 3.6).
$ \mathcal { F } $
, as this is a torsion class in the heart (see Remark 3.6).
By Theorem 3.7, this simple object
![]() $ S $
corresponds to a torsion-free, almost torsion module for
$ S $
corresponds to a torsion-free, almost torsion module for
![]() $ \mathcal {F} $
.
$ \mathcal {F} $
.
Remark 3.19. A different proof for the existence of torsion-free, almost torsion modules can be obtained using model-theoretic arguments, related to the link with critical summands of cotilting modules. More details on these appear in [Reference Angeleri Hügel, Herzog and Laking2].
Recall that a finite-dimensional module
![]() $ S \ne 0 $
is simple with respect to a torsion-free class (see [Reference Enomoto16]), if it satisfies conditions (1) and (2) in Definition 3.1.
$ S \ne 0 $
is simple with respect to a torsion-free class (see [Reference Enomoto16]), if it satisfies conditions (1) and (2) in Definition 3.1.
Notice that a simple module for some torsion-free class
![]() $ \mathbf {f} $
in
$ \mathbf {f} $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
automatically satisfies conditions (1) and (2) for any extension of
$\mathrm {mod} $
automatically satisfies conditions (1) and (2) for any extension of
![]() $ \mathbf {f} $
to
$ \mathbf {f} $
to
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
.
$\mathrm {Mod} $
.
Proposition 3.20. Let
![]() $ \mathcal {F} $
and
$ \mathcal {F} $
and
![]() $ \mathcal {F}' $
be definable torsion-free classes in
$ \mathcal {F}' $
be definable torsion-free classes in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
such that the torsion-free, almost torsion modules for
$\mathrm {Mod} $
such that the torsion-free, almost torsion modules for
![]() $ \mathcal {F} $
and
$ \mathcal {F} $
and
![]() $ \mathcal {F}'$
coincide. Then
$ \mathcal {F}'$
coincide. Then
![]() $ \mathcal {F} = \mathcal {F}'$
.
$ \mathcal {F} = \mathcal {F}'$
.
Moreover, every finite-dimensional simple object for
![]() $ \mathcal {F}$
embeds in some torsion-free, almost torsion module.
$ \mathcal {F}$
embeds in some torsion-free, almost torsion module.
Proof. Since the torsion-free classes are definable, by Theorem 2.14, it is enough to prove that
![]() $ \mathcal {F}\, \cap \, \Lambda $
-
$ \mathcal {F}\, \cap \, \Lambda $
-
![]() $\mathrm {mod} = \mathcal {F}' \cap \Lambda $
-
$\mathrm {mod} = \mathcal {F}' \cap \Lambda $
-
![]() $\mathrm {mod} $
.
$\mathrm {mod} $
.
By [Reference Enomoto16, Th. 3.15], we know that torsion-free classes in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
are determined by their simple objects.
$\mathrm {mod} $
are determined by their simple objects.
Assume without loss of generality that
![]() $ \mathcal {F} \ne 0 $
. Let
$ \mathcal {F} \ne 0 $
. Let
![]() $ B \in \mathcal {F} \cap \Lambda $
-
$ B \in \mathcal {F} \cap \Lambda $
-
![]() $\mathrm {mod} $
be a simple object in the torsion-free class.
$\mathrm {mod} $
be a simple object in the torsion-free class.
Then, by Lemma 3.16,
![]() $ B $
is a finitely generated object in the heart associated with
$ B $
is a finitely generated object in the heart associated with
![]() $ \mathcal {F} $
, whence it admits a simple quotient
$ \mathcal {F} $
, whence it admits a simple quotient
![]() $ S $
. In the heart,
$ S $
. In the heart,
![]() $ B $
is an object of the torsion class
$ B $
is an object of the torsion class
![]() $ \mathcal {F} $
, and therefore
$ \mathcal {F} $
, and therefore
![]() $ S \in \mathcal {F}$
.
$ S \in \mathcal {F}$
.
It follows, by Theorem 3.7, that there is a torsion-free, almost torsion module
![]() $ S $
for
$ S $
for
![]() $ \mathcal {F}$
, together with a nonzero homomorphism
$ \mathcal {F}$
, together with a nonzero homomorphism
![]() $ f : B \to S $
.
$ f : B \to S $
.
Since
![]() $ B $
is simple in the torsion-free class,
$ B $
is simple in the torsion-free class,
![]() $ f $
must be a monomorphism, whence
$ f $
must be a monomorphism, whence
![]() $ B $
is a submodule of
$ B $
is a submodule of
![]() $ S $
which is by assumption an element of
$ S $
which is by assumption an element of
![]() $ \mathcal {F}' $
.
$ \mathcal {F}' $
.
This procedure shows that all the simple objects in
![]() $ \mathcal {F} \cap \Lambda $
-
$ \mathcal {F} \cap \Lambda $
-
![]() $\mathrm {mod} $
are contained in
$\mathrm {mod} $
are contained in
![]() $ \mathcal {F}' \cap \Lambda $
-
$ \mathcal {F}' \cap \Lambda $
-
![]() $\mathrm {mod} $
.
$\mathrm {mod} $
.
Whence
![]() $ \mathcal {F} \cap \Lambda $
-
$ \mathcal {F} \cap \Lambda $
-
![]() $\mathrm {mod} \subseteq \mathcal {F}' \cap \Lambda $
-
$\mathrm {mod} \subseteq \mathcal {F}' \cap \Lambda $
-
![]() $\mathrm {mod} $
. The same argument works for the opposite inclusion.
$\mathrm {mod} $
. The same argument works for the opposite inclusion.
Remark 3.21. Minimal extending modules (i.e., finite-dimensional torsion-free, almost torsion modules) do not provide enough information to determine a torsion-free class in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
as already observed in [Reference Asai and Pfeifer6], [Reference Enomoto16].
$\mathrm {mod} $
as already observed in [Reference Asai and Pfeifer6], [Reference Enomoto16].
This shows that the role of infinite-dimensional torsion-free, almost torsion modules is not negligible in the study of torsion pairs of
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
.
$\mathrm {mod} $
.
4 The lattice of torsion classes
There is a natural partial order on the collection of torsion classes
![]() $ \mathbf {tors}(\Lambda ) $
of
$ \mathbf {tors}(\Lambda ) $
of
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
given by inclusion.
$\mathrm {mod} $
given by inclusion.
As shown in [Reference Demonet, Iyama, Reading, Reiten and Thomas15], the resulting poset has the structure of a complete lattice and enjoys several nice lattice-theoretic properties.
More explicitly, we have the following description of the meet and join of a set indexed family
![]() $ \{ \mathbf {t}_i \}_{i \in I} $
of torsion classes:
$ \{ \mathbf {t}_i \}_{i \in I} $
of torsion classes:
 $$\begin{align*}\bigwedge_{I} \mathbf{t}_i := \bigcap_I \mathbf{t}_i \quad, \quad \bigvee \mathbf{t}_i := \widetilde{\mathbf{T}}\Big( \bigcup_I \mathbf{t}_i \Big). \end{align*}$$
$$\begin{align*}\bigwedge_{I} \mathbf{t}_i := \bigcap_I \mathbf{t}_i \quad, \quad \bigvee \mathbf{t}_i := \widetilde{\mathbf{T}}\Big( \bigcup_I \mathbf{t}_i \Big). \end{align*}$$
We recall also some basic lattice theoretic terminology.
Definition 4.1. Let
![]() $ (L, \le ) $
be a poset,
$ (L, \le ) $
be a poset,
![]() $ x, y \in L $
:
$ x, y \in L $
:
-
(1) The interval
 $ [ x, y ] $
is the poset supported by those
$ [ x, y ] $
is the poset supported by those
 $ z \in L $
with
$ z \in L $
with
 $ x \le z \le y $
. Notice that if
$ x \le z \le y $
. Notice that if
 $ L $
is a (complete) lattice, any nonempty interval in
$ L $
is a (complete) lattice, any nonempty interval in
 $ L $
is a (complete) sublattice of
$ L $
is a (complete) sublattice of
 $ L $
.
$ L $
. -
(2) We say that
 $ y $
covers
$ y $
covers
 $ x $
if
$ x $
if
 $ x < y $
and for any
$ x < y $
and for any
 $ z \in L $
such that
$ z \in L $
such that
 $ x \le z \le y $
, either
$ x \le z \le y $
, either
 $ z = x $
or
$ z = x $
or
 $ z = y $
.
$ z = y $
. -
(3) Let
 $ L $
be a lattice. An element
$ L $
be a lattice. An element
 $ x $
is meet irreducible if whenever
$ x $
is meet irreducible if whenever
 $ x = y \wedge z $
we must have
$ x = y \wedge z $
we must have
 $ x = y $
or
$ x = y $
or
 $ x = z $
. If
$ x = z $
. If
 $ L $
is complete, an element
$ L $
is complete, an element
 $ x $
is completely meet irreducible if whenever
$ x $
is completely meet irreducible if whenever
 $ x = \bigwedge _{I} y_i $
, with
$ x = \bigwedge _{I} y_i $
, with
 $ y_i \in L $
, we must have
$ y_i \in L $
, we must have
 $ x = y_j $
for some
$ x = y_j $
for some
 $ j \in I $
.
$ j \in I $
.This condition can be restated as follows: there is a unique element
 $ x^\star $
covering
$ x^\star $
covering
 $ x $
, and for every
$ x $
, and for every
 $ y> x $
we have
$ y> x $
we have
 $ y \ge x^\star $
.
$ y \ge x^\star $
. -
(3’) Let
 $ L $
be a lattice. An element
$ L $
be a lattice. An element
 $ x $
is join irreducible if whenever
$ x $
is join irreducible if whenever
 $ x = y \vee z $
we must have
$ x = y \vee z $
we must have
 $ x = y $
or
$ x = y $
or
 $ x = z $
. If
$ x = z $
. If
 $ L $
is complete, an element
$ L $
is complete, an element
 $ x $
is completely join irreducible if whenever
$ x $
is completely join irreducible if whenever
 $ x = \bigvee _{I} y_i $
, with
$ x = \bigvee _{I} y_i $
, with
 $ y_i \in L $
, we must have
$ y_i \in L $
, we must have
 $ x = y_j $
for some
$ x = y_j $
for some
 $ j \in I $
.
$ j \in I $
.This condition can be restated as follows: there is a unique element
 $ x^\star $
covered by
$ x^\star $
covered by
 $ x $
, and for every
$ x $
, and for every
 $ y < x $
we have
$ y < x $
we have
 $ y \le x^\star $
.
$ y \le x^\star $
. -
(4) A poset
 $ L $
has finite length if every chain in
$ L $
has finite length if every chain in
 $ L $
stabilizes.
$ L $
stabilizes.
We recall a result proved in [Reference Barnard, Carroll and Zhu8], relating minimal extending modules with the covering relation in
![]() $ \mathbf {tors}(\Lambda ) $
.
$ \mathbf {tors}(\Lambda ) $
.
Theorem 4.2 [Reference Barnard, Carroll and Zhu8, Th. 1.0.2].
Let
![]() $ \mathbf { t } \in \mathbf {tors}(\Lambda ) $
, and let
$ \mathbf { t } \in \mathbf {tors}(\Lambda ) $
, and let
![]() $ \mathcal {S} $
be a collection of representatives of the isoclasses of minimal extending modules for
$ \mathcal {S} $
be a collection of representatives of the isoclasses of minimal extending modules for
![]() $(\mathbf {t}, \mathbf {t}^{\perp _0})$
.
$(\mathbf {t}, \mathbf {t}^{\perp _0})$
.
Then the elements of
![]() $ \mathcal {S}$
are in bijection with torsion classes covering
$ \mathcal {S}$
are in bijection with torsion classes covering
![]() $ \mathbf {t} $
.
$ \mathbf {t} $
.
A typical phenomenon for the lattice of torsion pairs in the
![]() $ \tau $
-tilting infinite case is the presence of nontrivial locally maximal elements.
$ \tau $
-tilting infinite case is the presence of nontrivial locally maximal elements.
Definition 4.3. Let
![]() $ \mathbf { t } \in \mathbf {tors}(\Lambda ) $
. We say that
$ \mathbf { t } \in \mathbf {tors}(\Lambda ) $
. We say that
![]() $ \mathbf { t } $
is locally maximal if there are no elements of
$ \mathbf { t } $
is locally maximal if there are no elements of
![]() $ \mathbf { tors }(\Lambda ) $
covering
$ \mathbf { tors }(\Lambda ) $
covering
![]() $ \mathbf {t} $
.
$ \mathbf {t} $
.
Remark 4.4. Any locally maximal torsion class is obtained as the meet of all the strictly larger torsion classes. In particular, such classes are never completely meet irreducible.
Furthermore, notice that there is a unique functorially finite locally maximal element, namely the torsion class
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
, which is by definition the meet of the empty set.
$\mathrm {mod} $
, which is by definition the meet of the empty set.
In fact, for any functorially finite torsion class
![]() $ \mathbf {t} $
properly contained in some other class
$ \mathbf {t} $
properly contained in some other class
![]() $ \mathbf {u} $
, it is possible, by means of mutation, to find a class
$ \mathbf {u} $
, it is possible, by means of mutation, to find a class
![]() $ \mathbf {t}^{\star } $
covering
$ \mathbf {t}^{\star } $
covering
![]() $ \mathbf {t} $
such that
$ \mathbf {t} $
such that
![]() $ \mathbf {t}^{\star } \le \mathbf {u} $
. See [Reference Demonet, Iyama and Jasso14, Th. 3.1].
$ \mathbf {t}^{\star } \le \mathbf {u} $
. See [Reference Demonet, Iyama and Jasso14, Th. 3.1].
Lemma 4.5. Let
![]() $ \mathbf { t } \in \mathbf { tors }(\Lambda ) $
be a meet irreducible, but not completely meet irreducible element, then
$ \mathbf { t } \in \mathbf { tors }(\Lambda ) $
be a meet irreducible, but not completely meet irreducible element, then
![]() $ \mathbf { t } $
is locally maximal.
$ \mathbf { t } $
is locally maximal.
Proof. Assume by contradiction that
![]() $ \mathbf {t} $
has some covering class. By meet irreducibility, it has precisely one, say
$ \mathbf {t} $
has some covering class. By meet irreducibility, it has precisely one, say
![]() $\mathbf { t }^\star $
.
$\mathbf { t }^\star $
.
As
![]() $ \mathbf {t} $
is not completely meet-irreducible, but it has just one covering class, there must be some torsion class
$ \mathbf {t} $
is not completely meet-irreducible, but it has just one covering class, there must be some torsion class
![]() $ \mathbf { u } \supsetneq \mathbf { t } $
such that
$ \mathbf { u } \supsetneq \mathbf { t } $
such that
![]() $ \mathbf { u } \not \supseteq \mathbf { t }^\star $
.
$ \mathbf { u } \not \supseteq \mathbf { t }^\star $
.
However, this is absurd, since
![]() $ \mathbf { u } \wedge \mathbf { t }^\star = \mathbf { t } $
. So
$ \mathbf { u } \wedge \mathbf { t }^\star = \mathbf { t } $
. So
![]() $ \mathbf { t } $
is locally maximal.
$ \mathbf { t } $
is locally maximal.
Example 4.6. We discuss the most common example of a torsion pair without minimal extending modules. Let
![]() $ k $
be an algebraically closed field.
$ k $
be an algebraically closed field.
Let
![]() $ \Lambda = kK_2 $
be the Kronecker algebra, obtained as the path algebra of the quiver
$ \Lambda = kK_2 $
be the Kronecker algebra, obtained as the path algebra of the quiver
![]() .
.
This is a finite-dimensional tame hereditary algebra, and as such, we have that any indecomposable in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
is contained in the preprojective
$\mathrm {mod} $
is contained in the preprojective
![]() $ \mathbf {p} $
, regular
$ \mathbf {p} $
, regular
![]() $ \mathbf {r} $
, or preinjective
$ \mathbf {r} $
, or preinjective
![]() $ \mathbf {q} $
component of the AR-quiver.
$ \mathbf {q} $
component of the AR-quiver.
Recall that the additive closure of the regular component
![]() $ \mathbf {r} $
is a wide subcategory of
$ \mathbf {r} $
is a wide subcategory of
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
whose simple objects are called simple regular modules.
$\mathrm {mod} $
whose simple objects are called simple regular modules.
The torsion class generated by the modules in the regular component
![]() $ \widetilde {\mathbf {T}}(\mathbf {r}) $
contains all the regular and preinjective modules, but no preprojective module.
$ \widetilde {\mathbf {T}}(\mathbf {r}) $
contains all the regular and preinjective modules, but no preprojective module.
The preprojective component contains a countable collection of bricks
![]() $ P_i $
, such that
$ P_i $
, such that
![]() $ \widetilde {\mathbf {T}}(P_i) \supset \widetilde {\mathbf {T}}(P_{i + 1}) $
. Moreover,
$ \widetilde {\mathbf {T}}(P_i) \supset \widetilde {\mathbf {T}}(P_{i + 1}) $
. Moreover,
![]() $ \bigcap \widetilde {\mathbf {T}}(P_i) = \widetilde {\mathbf {T}}(\mathbf {r} ) $
.
$ \bigcap \widetilde {\mathbf {T}}(P_i) = \widetilde {\mathbf {T}}(\mathbf {r} ) $
.
Any torsion class larger than
![]() $ \widetilde {\mathbf {T}}(\mathbf {r}) $
is of the form
$ \widetilde {\mathbf {T}}(\mathbf {r}) $
is of the form
![]() $ \widetilde {\mathbf {T}}(P_i) $
for some
$ \widetilde {\mathbf {T}}(P_i) $
for some
![]() $ P_i $
, so it follows that
$ P_i $
, so it follows that
![]() $ \widetilde {\mathbf {T}}(\mathbf {r}) $
is locally maximal.
$ \widetilde {\mathbf {T}}(\mathbf {r}) $
is locally maximal.
Consider now the corresponding cosilting torsion pair
![]() $ ( {\mathbf {T}}(\mathbf {r}), \mathbf {r}^{\perp _0} ) $
in
$ ( {\mathbf {T}}(\mathbf {r}), \mathbf {r}^{\perp _0} ) $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
(see Figure 1). By Corollary 3.18, we know that there must be some torsion-free, almost torsion module for this torsion pair, which is necessarily infinite-dimensional as the corresponding torsion pair in
$\mathrm {Mod} $
(see Figure 1). By Corollary 3.18, we know that there must be some torsion-free, almost torsion module for this torsion pair, which is necessarily infinite-dimensional as the corresponding torsion pair in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
has no minimal extending modules.
$\mathrm {mod} $
has no minimal extending modules.

Figure 1 Torsion pairs in
![]() $ kK_2$
-
$ kK_2$
-
![]() $\mathrm {mod}$
.
$\mathrm {mod}$
.
It is easy to compute the torsion, almost torsion-free modules for this torsion pair: they are precisely the simple regular modules
![]() $ \{S_l\}_{L} $
.
$ \{S_l\}_{L} $
.
By Corollary 3.9, it follows that the torsion-free, almost torsion modules must lie in the orthogonal category
![]() $ (\{ S_{l}\}_{L})^{\perp _{0,1}} $
which is known to be equivalent to the module category
$ (\{ S_{l}\}_{L})^{\perp _{0,1}} $
which is known to be equivalent to the module category
![]() $ k(X)$
-
$ k(X)$
-
![]() $\mathrm {Mod} $
.
$\mathrm {Mod} $
.
Such a subcategory contains a unique brick, up to isomorphism, since
![]() $ k(X) $
is a field, and this brick is the generic module
$ k(X) $
is a field, and this brick is the generic module
![]() $ G $
described by Ringel [Reference Ringel26, Sec. 5.7, Th. 5.3].
$ G $
described by Ringel [Reference Ringel26, Sec. 5.7, Th. 5.3].
Since a torsion-free, almost torsion module must exist, we conclude that
![]() $ G $
is the unique torsion-free, almost torsion module for the extended torsion pair.
$ G $
is the unique torsion-free, almost torsion module for the extended torsion pair.
4.1 Locally maximal torsion classes for
 $ \tau $
-tilting infinite algebras
$ \tau $
-tilting infinite algebras
We need some preparations to show the existence of non-functorially finite locally maximal torsion classes.
Definition 4.7. Let
![]() $ L $
be a complete lattice. An element
$ L $
be a complete lattice. An element
![]() $ x \in L $
is compact if for every set-indexed family
$ x \in L $
is compact if for every set-indexed family
![]() $ \{y_i\}_{i \in I} $
such that
$ \{y_i\}_{i \in I} $
such that
![]() $ x \le \bigvee _{i \in I} y_i $
there exists a finite subset
$ x \le \bigvee _{i \in I} y_i $
there exists a finite subset
![]() $ J \subseteq I $
such that
$ J \subseteq I $
such that
![]() $ x \le \bigvee _{i \in J} y_i $
. Dually, we have the notion of a co-compact element.
$ x \le \bigvee _{i \in J} y_i $
. Dually, we have the notion of a co-compact element.
We use the following observation (the contrapositive of [Reference Demonet, Iyama and Jasso14, Lemma 3.10]).
Lemma 4.8. Let
![]() $ \mathbf { t } \in \mathbf { tors }(\Lambda ) $
be a functorially finite torsion class. Let
$ \mathbf { t } \in \mathbf { tors }(\Lambda ) $
be a functorially finite torsion class. Let
![]() $ \{ \mathbf { t }_i \} $
be a chain of torsion classes indexed by some ordinal.
$ \{ \mathbf { t }_i \} $
be a chain of torsion classes indexed by some ordinal.
If
![]() $ \mathbf { t } = \bigvee _i \mathbf { t }_i $
, then there exists some
$ \mathbf { t } = \bigvee _i \mathbf { t }_i $
, then there exists some
![]() $ j $
such that
$ j $
such that
![]() $ \mathbf {t}_j = \mathbf {t} $
.
$ \mathbf {t}_j = \mathbf {t} $
.
Proof. Any functorially finite torsion class is both compact and co-compact [Reference Demonet, Iyama, Reading, Reiten and Thomas15, Prop. 3.2], in particular, there exists a finite subchain
![]() $ \mathbf { t }_{i_n} $
such that
$ \mathbf { t }_{i_n} $
such that
![]() $ \mathbf { t } = \bigvee _n \mathbf { t }_{i_n} $
. Whence,
$ \mathbf { t } = \bigvee _n \mathbf { t }_{i_n} $
. Whence,
![]() $ \mathbf {t}_j = \mathbf {t} $
for some
$ \mathbf {t}_j = \mathbf {t} $
for some
![]() $ j $
.
$ j $
.
Lemma 4.9. Let
![]() $ \mathbf { u }_1, \mathbf { u }_2 $
be functorially finite torsion classes in
$ \mathbf { u }_1, \mathbf { u }_2 $
be functorially finite torsion classes in
![]() $ \Lambda $
-mod, and let
$ \Lambda $
-mod, and let
![]() $ I = [ \mathbf { u }_1, \mathbf { u }_2 ] \subseteq \mathbf { tors }(\Lambda ) $
be the corresponding interval.
$ I = [ \mathbf { u }_1, \mathbf { u }_2 ] \subseteq \mathbf { tors }(\Lambda ) $
be the corresponding interval.
Then, if
![]() $ I $
has not finite length, it contains a maximal and a minimal non-functorially finite torsion class
$ I $
has not finite length, it contains a maximal and a minimal non-functorially finite torsion class
![]() $ \mathbf {t}_{max} $
and
$ \mathbf {t}_{max} $
and
![]() $ \mathbf { t }_{min} $
.
$ \mathbf { t }_{min} $
.
Moreover,
![]() $ \mathbf {t}_{max} $
is meet irreducible in
$ \mathbf {t}_{max} $
is meet irreducible in
![]() $ I $
but not completely meet irreducible, whereas
$ I $
but not completely meet irreducible, whereas
![]() $ \mathbf { t }_{min} $
is join irreducible in
$ \mathbf { t }_{min} $
is join irreducible in
![]() $ I $
but not completely join irreducible.
$ I $
but not completely join irreducible.
Proof. We denote by
![]() $ \mathbf {nftors}(\Lambda ) \subset \mathbf {tors}(\Lambda ) $
the poset of non-functorially finite torsion classes.
$ \mathbf {nftors}(\Lambda ) \subset \mathbf {tors}(\Lambda ) $
the poset of non-functorially finite torsion classes.
By assumption,
![]() $ I $
must contain either an infinite strictly ascending chain or an infinite strictly descending chain.
$ I $
must contain either an infinite strictly ascending chain or an infinite strictly descending chain.
Since
![]() $ I $
is a complete sublattice, the join of the first chain, or the meet of the second one yields a non-functorially finite class lying in
$ I $
is a complete sublattice, the join of the first chain, or the meet of the second one yields a non-functorially finite class lying in
![]() $ I $
(using compactness, or co-compactness of functorially finite torsion classes), proving that the poset
$ I $
(using compactness, or co-compactness of functorially finite torsion classes), proving that the poset
![]() $ nI = I \cap \mathbf {nftors}(\Lambda ) $
is not empty.
$ nI = I \cap \mathbf {nftors}(\Lambda ) $
is not empty.
This poset and its dual satisfy the hypotheses of Zorn’s lemma; in fact, for any chain in
![]() $ nI $
, the join, or meet, of the chain in
$ nI $
, the join, or meet, of the chain in
![]() $ I $
is again a non-functorially finite torsion class by Lemma 4.8 and its dual, giving the required upper, or lower, bound.
$ I $
is again a non-functorially finite torsion class by Lemma 4.8 and its dual, giving the required upper, or lower, bound.
So we conclude that
![]() $ nI $
has a maximal and a minimal element.
$ nI $
has a maximal and a minimal element.
Now, if
![]() $ \mathbf { t } $
is such a maximal element, then starting with the obvious inclusion
$ \mathbf { t } $
is such a maximal element, then starting with the obvious inclusion
![]() $ \mathbf { t } \subsetneq \mathbf {u}_2 $
and applying inductively [Reference Demonet, Iyama and Jasso14, Th. 3.1], it is possible to construct an infinite descending chain of functorially finite torsion classes
$ \mathbf { t } \subsetneq \mathbf {u}_2 $
and applying inductively [Reference Demonet, Iyama and Jasso14, Th. 3.1], it is possible to construct an infinite descending chain of functorially finite torsion classes
![]() $ \mathbf { t } \subseteq \cdots \subsetneq \mathbf { t }_n \subsetneq \dots \subsetneq \mathbf { t }_1 \subsetneq \mathbf { t }_0 = \mathbf {u}_2 $
.
$ \mathbf { t } \subseteq \cdots \subsetneq \mathbf { t }_n \subsetneq \dots \subsetneq \mathbf { t }_1 \subsetneq \mathbf { t }_0 = \mathbf {u}_2 $
.
Now, by co-compactness, the meet of an infinite strictly descending chain is not functorially finite, whence we can conclude by maximality that
![]() $ \mathbf { t } = \bigwedge _{ i \in \mathbb {N}} \mathbf {t}_i $
, proving that it is not completely meet irreducible.
$ \mathbf { t } = \bigwedge _{ i \in \mathbb {N}} \mathbf {t}_i $
, proving that it is not completely meet irreducible.
Assume now that
![]() $ \mathbf { t } = \mathbf { s}_1 \wedge \mathbf {s}_2 $
, for some
$ \mathbf { t } = \mathbf { s}_1 \wedge \mathbf {s}_2 $
, for some
![]() $ \mathbf { s }_i \in I $
.
$ \mathbf { s }_i \in I $
.
By the definition of meet,
![]() $ \mathbf { t } \le \mathbf { s }_i $
, so if any of the two is not functorially finite, we must have equality, by maximality in
$ \mathbf { t } \le \mathbf { s }_i $
, so if any of the two is not functorially finite, we must have equality, by maximality in
![]() $ nI $
.
$ nI $
.
So assume that they are both functorially finite. By the argument above,
![]() $ \mathbf { t } = \bigwedge _{ i \in \mathbb {N}} \mathbf {t}_i $
, but by co-compactness of
$ \mathbf { t } = \bigwedge _{ i \in \mathbb {N}} \mathbf {t}_i $
, but by co-compactness of
![]() $ \mathbf {s}_i $
, there is some index
$ \mathbf {s}_i $
, there is some index
![]() $ j $
, such that
$ j $
, such that
![]() $ \mathbf { t }_j \le \mathbf {s}_1, \mathbf { s }_2 $
, but this is a contradiction, since
$ \mathbf { t }_j \le \mathbf {s}_1, \mathbf { s }_2 $
, but this is a contradiction, since
![]() $ \mathbf {t}_j> \mathbf {t} $
. So maximal non-functorially finite torsion classes are meet irreducible in
$ \mathbf {t}_j> \mathbf {t} $
. So maximal non-functorially finite torsion classes are meet irreducible in
![]() $ I $
.
$ I $
.
Dual arguments yield the dual results.
Corollary 4.10. Let
![]() $ \Lambda $
be a
$ \Lambda $
be a
![]() $ \tau $
-tilting infinite algebra, then there exists a maximal non-functorially finite torsion class. Such torsion class is meet irreducible, but not completely meet irreducible, hence locally maximal.
$ \tau $
-tilting infinite algebra, then there exists a maximal non-functorially finite torsion class. Such torsion class is meet irreducible, but not completely meet irreducible, hence locally maximal.
Proof. Apply the lemma above to the interval
![]() $ [0, \Lambda $
-
$ [0, \Lambda $
-
![]() $\mathrm {mod} ] $
, which has infinite length (see [Reference Demonet, Iyama and Jasso14, Prop. 3.9]), to obtain a maximal element
$\mathrm {mod} ] $
, which has infinite length (see [Reference Demonet, Iyama and Jasso14, Prop. 3.9]), to obtain a maximal element
![]() $ \mathbf {t} $
in
$ \mathbf {t} $
in
![]() $ \mathbf {nftors}(\Lambda ) $
with the required properties.
$ \mathbf {nftors}(\Lambda ) $
with the required properties.
4.2 The main theorem
We need a last lemma before proceeding into the proof of the main theorem. This construction is already present in the literature (see [Reference Barnard, Carroll and Zhu8]), and we give a proof for the convenience of the reader.
Lemma 4.11. Let
![]() $ B \in \Lambda $
-
$ B \in \Lambda $
-
![]() $\mathrm {Mod} $
be a brick. Then
$\mathrm {Mod} $
be a brick. Then
![]() $ B $
is the unique torsion, almost torsion-free module for the torsion pair
$ B $
is the unique torsion, almost torsion-free module for the torsion pair
![]() $ ( \mathbf {T}(B), B^{\perp _0}) $
.
$ ( \mathbf {T}(B), B^{\perp _0}) $
.
Proof. We check the three conditions dual to those in Definition 3.1:
(1)
![]() $ B \in \mathbf {T}(B) $
by definition.
$ B \in \mathbf {T}(B) $
by definition.
(2) Since
![]() $ B $
is a brick, for every proper submodule
$ B $
is a brick, for every proper submodule
![]() $ M $
of
$ M $
of
![]() $ B $
, we must have
$ B $
, we must have
![]() $ M \in B^{\perp _0} $
, that is,
$ M \in B^{\perp _0} $
, that is,
![]() $ M $
is torsion-free.
$ M $
is torsion-free.
(3’) Consider a short exact sequence
with
![]() $ F \in B^{\perp _0} $
. If
$ F \in B^{\perp _0} $
. If
![]() $ M \not \in B^{\perp _0} $
, let
$ M \not \in B^{\perp _0} $
, let
![]() $ 0 \ne g : B \to M $
. Since
$ 0 \ne g : B \to M $
. Since
![]() $ F $
is torsion-free,
$ F $
is torsion-free,
![]() $ g $
cannot factor through
$ g $
cannot factor through
![]() $ F $
, in particular
$ F $
, in particular
![]() $ f \circ g \ne 0 $
.
$ f \circ g \ne 0 $
.
Since
![]() $ B $
is a brick, this endomorphism must be invertible, which means that the sequence splits. This proves that
$ B $
is a brick, this endomorphism must be invertible, which means that the sequence splits. This proves that
![]() $ B $
is torsion, almost torsion-free.
$ B $
is torsion, almost torsion-free.
Any other torsion, almost torsion-free module
![]() $ S $
, if not isomorphic to
$ S $
, if not isomorphic to
![]() $ B $
, would be orthogonal to it, in particular torsion-free. This is a contradiction, yielding uniqueness (up to isomorphism).
$ B $
, would be orthogonal to it, in particular torsion-free. This is a contradiction, yielding uniqueness (up to isomorphism).
Lemma 4.12. Let
![]() $ \Lambda $
be a
$ \Lambda $
be a
![]() $ \tau $
-tilting finite algebra. Then every brick in
$ \tau $
-tilting finite algebra. Then every brick in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
is finite-dimensional.
$\mathrm {Mod} $
is finite-dimensional.
Proof. Let
![]() $ B $
be a brick. By Lemma 4.11, the module
$ B $
be a brick. By Lemma 4.11, the module
![]() $ B $
is torsion, almost torsion-free with respect to
$ B $
is torsion, almost torsion-free with respect to
![]() $ ( \mathbf {T}(B), B^{\perp _0}) $
.
$ ( \mathbf {T}(B), B^{\perp _0}) $
.
The restriction of
![]() $ ( \mathbf {T}(B), B^{\perp _0}) $
to
$ ( \mathbf {T}(B), B^{\perp _0}) $
to
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
is necessarily functorially finite, as all torsion classes in
$\mathrm {mod} $
is necessarily functorially finite, as all torsion classes in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod} $
are functorially finite by hypothesis.
$\mathrm {mod} $
are functorially finite by hypothesis.
By Proposition 3.14,
![]() $ ( \mathbf {T}(B), B^{\perp _0}) $
is the unique extension of the functorially finite torsion pair obtained above.
$ ( \mathbf {T}(B), B^{\perp _0}) $
is the unique extension of the functorially finite torsion pair obtained above.
Whence, by Corollary 3.15, all the torsion, almost torsion-free and torsion-free, almost torsion modules for
![]() $ ( \mathbf {T}(B), B^{\perp _0}) $
are finite-dimensional.
$ ( \mathbf {T}(B), B^{\perp _0}) $
are finite-dimensional.
In particular, the brick
![]() $ B $
is finite-dimensional.
$ B $
is finite-dimensional.
Lemma 4.13. Let
![]() $ \Lambda $
be a
$ \Lambda $
be a
![]() $ \tau $
-tilting infinite algebra. Then there exists some infinite-dimensional brick in
$ \tau $
-tilting infinite algebra. Then there exists some infinite-dimensional brick in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {Mod} $
.
$\mathrm {Mod} $
.
Proof. Apply Corollary 4.10 to obtain a locally maximal non-functorially finite torsion class
![]() $ \mathbf {t} $
in
$ \mathbf {t} $
in
![]() $ \Lambda $
-
$ \Lambda $
-
![]() $\mathrm {mod}$
.
$\mathrm {mod}$
.
By Theorem 4.2, the corresponding torsion pair
![]() $ ( \mathbf {t},\mathbf {f} ) $
has no minimal extending modules.
$ ( \mathbf {t},\mathbf {f} ) $
has no minimal extending modules.
Consider now the corresponding torsion pair under the bijection in Theorem 2.14:
By Corollary 3.18, there is some torsion-free, almost torsion module
![]() $ B $
for this torsion pair.
$ B $
for this torsion pair.
If
![]() $ B $
were finite-dimensional, by Proposition 3.11, it would be minimal extending for the original torsion pair
$ B $
were finite-dimensional, by Proposition 3.11, it would be minimal extending for the original torsion pair
![]() $ (\mathbf {t},\mathbf {f}), $
which gives a contradiction.
$ (\mathbf {t},\mathbf {f}), $
which gives a contradiction.
Combining the two lemmas, we can finally obtain the following theorem.
Theorem 4.14. A finite-dimensional algebra
![]() $ \Lambda $
is
$ \Lambda $
is
![]() $ \tau $
-tilting finite if and only if every brick over
$ \tau $
-tilting finite if and only if every brick over
![]() $\Lambda $
is finitely generated.
$\Lambda $
is finitely generated.
Acknowledgment
The author would like to thank his supervisor Lidia Angeleri Hügel for her guidance and support, and Rosanna Laking for many hours of interesting discussion on cosilting theory and related topics.