Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alperin, J. L.
Brauer, Richard
and
Gorenstein, Daniel
1970.
Finite groups with quasi-dihedral and wreathed Sylow 2-subgroups..
Transactions of the American Mathematical Society,
Vol. 151,
Issue. 1,
p.
1.
Fong, Paul
1970.
A Characterization of the Finite Simple Groups PSp(4,q), G2(q), D42(q), II.
Nagoya Mathematical Journal,
Vol. 39,
Issue. ,
p.
39.
Lyons, Richard
1972.
Evidence for a new finite simple group.
Journal of Algebra,
Vol. 20,
Issue. 3,
p.
540.
Harris, Morton E.
1972.
A Characterization of Odd Order Extensions of the Finite Simple Groups PSp(4, q), G2(q), .
Nagoya Mathematical Journal,
Vol. 45,
Issue. ,
p.
79.
Hering, Christoph
Kantor, William M.
and
Seitz, Gary M.
1972.
Finite groups with a split BN-pair of rank 1. I.
Journal of Algebra,
Vol. 20,
Issue. 3,
p.
435.
1973.
Locally Finite Groups.
Vol. 3,
Issue. ,
p.
193.
Fong, Paul
and
Seitz, Gary M.
1973.
Groups with a (B, N)-pair of rank 2. I.
Inventiones Mathematicae,
Vol. 21,
Issue. 1-2,
p.
1.
Harris, Morton E.
1974.
Finite groups with given sylow 2-subgroups an product fusions.
Communications in Algebra,
Vol. 2,
Issue. 2,
p.
143.
O'Nan, Michael E
1977.
Some characterizations by centralizers of elements of order 3.
Journal of Algebra,
Vol. 48,
Issue. 1,
p.
113.
Walls, Gary Lee
1977.
Products of finite simple groups.
Journal of Algebra,
Vol. 48,
Issue. 1,
p.
68.
Fomin, A. N.
1979.
Permutational characterization of certain mathieu groups.
Algebra and Logic,
Vol. 18,
Issue. 2,
p.
144.
Gorenstein, Daniel
1979.
The classification of finite simple groups I. Simple groups and local analysis.
Bulletin of the American Mathematical Society,
Vol. 1,
Issue. 1,
p.
43.
Brauer, Richard
1979.
Blocks of characters and structure of finite groups.
Bulletin of the American Mathematical Society,
Vol. 1,
Issue. 1,
p.
21.
Harris, Morton E
1981.
PSL(2, q) type 2-components and the unbalanced group conjecture.
Journal of Algebra,
Vol. 68,
Issue. 1,
p.
190.
Michler, Gerhard O
1983.
Non-solvable finite groups with cyclic sylow p-subgroups have non-principal p-blocks.
Journal of Algebra,
Vol. 83,
Issue. 1,
p.
179.
Tchakerian, K. B.
and
Gentchev, Ts. R.
1983.
On products of finite simple groups.
Archiv der Mathematik,
Vol. 41,
Issue. 5,
p.
385.
Aschbacher, Michael
2002.
Finite groups of G2(3)-type.
Journal of Algebra,
Vol. 257,
Issue. 2,
p.
197.
Korchagina, Inna
2003.
On a Theorem of P. Fong.
Nagoya Mathematical Journal,
Vol. 171,
Issue. ,
p.
197.
Konygin, A. V.
2007.
Sets with trivial global stabilizers for primitive permutation groups which are not almost simple.
Proceedings of the Steklov Institute of Mathematics,
Vol. 257,
Issue. S1,
p.
S100.
Carlson, Jon F.
Grodal, Jesper
Mazza, Nadia
and
Nakano, Daniel K.
2022.
Torsion free endotrivial modules for finite groups of Lie type.
Pacific Journal of Mathematics,
Vol. 317,
Issue. 2,
p.
239.

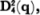 I
I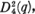 where
where 