Recently H. Hasse has given an interesting theory of Galois algebras, which generalizes the well known theory of Kummer fields; an algebra 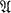over a field Ω is called a Galois algebra with Galois group G when 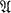possesses G as a group of automorphisms and 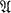is (G, Ω)-operator-isomorphic to the group ring G(Ω) of G over Ω. On assuming that the characteristic of Ω does not divide the order of G and that absolutely irreducible representations of G lie in Ω, Hasse constructs certain Ω-basis of 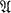, called factor basis, in accord with Wedderburn decomposition of the group ring and shows that a characterization of 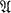is given by a certain matrix factor system which defines the multiplication between different parts of the factor basis belonging to different characters of G. Now the present work is to free the theory from the restriction on the characteristic. We can indeed embrace the case of non-semisimple modular group ring G(Ω).