Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T10:22:16.024Z Has data issue: false hasContentIssue false
  • English
  • Français

Descent for l-Adic Polylogarithms

Published online by Cambridge University Press:  11 January 2016

Jean-Claude Douai  and
Zdzisław Wojtkowiak
Jean-Claude Douai
Affiliation:
UFR de Mathématiques UMR AGAT CNRS Université des Sciences et Technologies de Lille, F-59655 Villeneuve d’Ascq Cedex, France, douai@agat.univ-lille1.fr
Zdzisław Wojtkowiak
Affiliation:
Université de Nice-Sophia Antipolis Département de Mathématiques Laboratoire Jean Alexandre Dieudonné U.R.A. au C.N.R.S., No 168 Parc Valrose - B.P.N° 71 06108 Nice Cedex 2, France, wojtkow@math.unice.fr, UFR de Mathématiques UMR AGAT CNRS Université des Sciences et Technologies de Lille,F-59655 Villeneuve d’Ascq Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L be a finite Galois extension of a number field K. Let G:= Gal(L/K). Let z1,…, zN ∊ L* \ {1} and let m1 …, mN ∊ ℚl. Let us assume that the linear combination of l-adic polylogarithms 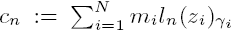(constructed in some given way) is a cocycle on GL and that the formal sum is G-invariant. Then we show that cn determines a unique cocycle sn on GK. We also prove a weak version of Zagier conjecture for l-adic dilogarithm. Finally we show that if c2 is “motivic” (m1,…, mN ∊ ℚ) then s2 is also “motivic”.

Keywords

11G55
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 192 , 2008 , pp. 59 - 88
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2008

References

[1] Beilinson, A. A. and Deligne, P., Interprétation motivique de la conjecture de Zagier reliant polylogarithmes et régulateurs, Motives (Jannsen, U., Kleiman, S. L. and Serre, J.-P., eds.), Proc. of Sym. in Pure Math. 55, Part II, AMS, 1994, pp. 97–121.Google Scholar
[2] Borel, A., Stable Real Cohomology of Arithmetic Groups, Ann. Scient. Ecole Norm. Sup., 4 série (1974), 235–272.CrossRefGoogle Scholar
[3] Ihara, Y., Profinite braid groups, Galois representations and complex multiplications, Annals of Math., 123 (1986), 43–106.Google Scholar
[4] Lewin, L., Polylogarithms and Associated Functions, North Holland, New York, Oxford, 1981.Google Scholar
[5] Soulé, Ch., K-théorie des anneaux d’entiers de corps de nombres et cohomologie etale, Inventiones math., 55 (1979), 251–295.CrossRefGoogle Scholar
[6] Suslin, A. A., Algebraic K-theory of Fields, Proc. of the Int. Congress of Math., Berkeley, California, USA, 1986, pp. 222–244.Google Scholar
[7] Suslin, A. A., K3 of a field and the Bloch group, Proc. of the Steklov Inst. of Math., 1991 (4), pp. 217–239.Google Scholar
[8] Wojtkowiak, Z., The Basic Structure of Polylogarithmic Functional Equations, Structural Properties of Polylogarithms (Lewin, L., ed.), Mathematical Surveys and Monographs, Vol. 37, pp. 205–231.Google Scholar
[9] Wojtkowiak, Z., On l-adic iterated integrals, I, Analog of Zagier Conjecture, Nagoya Math. Journal, 176 (2004), 113–158.Google Scholar
[10] Wojtkowiak, Z., On l-adic iterated integrals, II, Functional equations and l-adic polylogarithms, Nagoya Math. Journal, 177 (2005), 117–153.CrossRefGoogle Scholar
[11] Wojtkowiak, Z., On the Galois actions on torsors of paths I, Descent of Galois representations, J. Math. Sci. Univ. Tokyo, 14 (2007), 177–259.Google Scholar
[12] Wojtkowiak, Z., On l-adic iterated integrals, IV, Galois actions on fundamental groups, Ramifications and Generators, accepted in Math. Journal of Okayama University.Google Scholar
[13] Wojtkowiak, Z., A remark on Galois permutations of a tannakian category of mixtes Tate motives.Google Scholar
[14] Zagier, D., Polylogarithms, Dedekind Zeta functions and the Algebraic K-theory of fields, Arithmetic Algebraic Geometry (van der Geer, G., Oort, F. and Steenbrick, J., eds.), Prog. Math. Vol. 89, Birkhauser, Boston, 1991, pp. 391–430.Google Scholar