Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Onodera, Takeshi
1968.
Über Kogeneratoren.
Archiv der Mathematik,
Vol. 19,
Issue. 4,
p.
402.
Oberst, Ulrich
and
Schneider, Hans-J�rgen
1971.
Die Struktur von Projektiven Moduln.
Inventiones Mathematicae,
Vol. 13,
Issue. 4,
p.
295.
Sandomierski, F.L.
1972.
Ring Theory.
p.
333.
Mikhalev, A. V.
and
Skornyakov, L. A.
1972.
Algebra and Geometry.
p.
59.
Fisher, Joe W.
1973.
Finiteness conditions for projective and injective modules.
Proceedings of the American Mathematical Society,
Vol. 40,
Issue. 2,
p.
389.
Z�schinger, Helmut
1974.
Komplemente als direkte Summanden.
Archiv der Mathematik,
Vol. 25,
Issue. 1,
p.
241.
Zöschinger, Helmut
1974.
Komplementierte Moduln über Dedekindringen.
Journal of Algebra,
Vol. 29,
Issue. 1,
p.
42.
Nicholson, W. K.
1975.
On Semiperfect Modules.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 1,
p.
77.
Faith, Carl
1976.
Algebra II Ring Theory.
Vol. 191,
Issue. ,
p.
151.
Hauger, G.
1976.
Aufsteigende Kettenbedingung für Zyklische Moduln und Perfekte Endomorphismenringe.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 28,
Issue. 3-4,
p.
275.
Rangaswamy, K. M.
1977.
Modules with Finite Spanning Dimension.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 2,
p.
255.
Wisbauer, Robert
1978.
?-Semiperfekte und ?-perfekte Moduln.
Mathematische Zeitschrift,
Vol. 162,
Issue. 2,
p.
131.
Jansen, Willem G.
1978.
Fsp rings and modules, and local modules.
Communications in Algebra,
Vol. 6,
Issue. 6,
p.
617.
Ikeyama, Tamotsu
1980.
Splitting torsion theories.
Communications in Algebra,
Vol. 8,
Issue. 13,
p.
1267.
Ikeyama, Tamotsu
1981.
Four-fold torsion theories and rings of fractions.
Communications in Algebra,
Vol. 9,
Issue. 10,
p.
1027.
Haack, Joel K.
1982.
The Duals of the Camillo-Zelmanowitz Formulas for Goldie Dimension.
Canadian Mathematical Bulletin,
Vol. 25,
Issue. 3,
p.
325.
Generalov, A. I.
1983.
The ?-Cohigh purity in a category of modules.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 33,
Issue. 5,
p.
402.
García Hernández, J.L.
Gómez Pardo, J.L.
and
Martínez Hernández, J.
1986.
Semiperfect modules relative to a torsion theory.
Journal of Pure and Applied Algebra,
Vol. 43,
Issue. 2,
p.
145.
Garc�a, J. L.
and
G�mez Pardo, J. L.
1987.
On endomorphism rings of quasiprojective modules.
Mathematische Zeitschrift,
Vol. 196,
Issue. 1,
p.
87.
Varadarajan, K.
and
Wani, P. R.
1989.
Modules over endomorphism rings. II.
Acta Mathematica Hungarica,
Vol. 53,
Issue. 3-4,
p.
309.

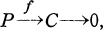 wobei
wobei 