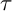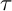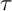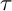1 Introduction
Throughout this note, k denotes an algebraically closed field and all algebras are assumed to be finite-dimensional over k, associative, and unital. We denote by
![]() $\operatorname{\mathrm{Mod}} \Lambda $
the category of all left
$\operatorname{\mathrm{Mod}} \Lambda $
the category of all left
![]() $\Lambda $
-modules, and
$\Lambda $
-modules, and
![]() $\operatorname{\mathrm{mod}} \Lambda $
denotes the full subcategory of finitely generated left
$\operatorname{\mathrm{mod}} \Lambda $
denotes the full subcategory of finitely generated left
![]() $\Lambda $
-modules. Let
$\Lambda $
-modules. Let
![]() $\operatorname{\mathrm{Ind}}(\Lambda )$
and
$\operatorname{\mathrm{Ind}}(\Lambda )$
and
![]() $\operatorname{\mathrm{ind}}(\Lambda )$
, respectively, denote the collections of all indecomposable modules in
$\operatorname{\mathrm{ind}}(\Lambda )$
, respectively, denote the collections of all indecomposable modules in
![]() $\operatorname{\mathrm{Mod}} \Lambda $
and
$\operatorname{\mathrm{Mod}} \Lambda $
and
![]() $\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphism. Then,
$\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphism. Then,
![]() $\Lambda $
is said to be representation-infinite (rep-inf, for short) if
$\Lambda $
is said to be representation-infinite (rep-inf, for short) if
![]() $\operatorname{\mathrm{ind}}(\Lambda )$
is infinite. In this work, we are primarily interested in rep-inf algebras, because the problems treated here are trivial over representation-finite algebras.
$\operatorname{\mathrm{ind}}(\Lambda )$
is infinite. In this work, we are primarily interested in rep-inf algebras, because the problems treated here are trivial over representation-finite algebras.
For our purposes in this paper, without loss of generality, we may always assume that
![]() $\Lambda $
is basic and connected. Thus, there is an isomorphism of algebras
$\Lambda $
is basic and connected. Thus, there is an isomorphism of algebras
![]() $\Lambda \simeq kQ/I$
, where Q is a finite connected quiver and I is an admissible ideal in the path algebra
$\Lambda \simeq kQ/I$
, where Q is a finite connected quiver and I is an admissible ideal in the path algebra
![]() $kQ$
. In particular,
$kQ$
. In particular,
![]() $|K_0(\Lambda )|=|Q_0|$
, meaning that the rank of the Grothendieck group
$|K_0(\Lambda )|=|Q_0|$
, meaning that the rank of the Grothendieck group
![]() $K_0(\Lambda )$
is the same as the number of vertices in Q. Consequently, each
$K_0(\Lambda )$
is the same as the number of vertices in Q. Consequently, each
![]() $\Lambda $
-module can be viewed as a representation of the bound quiver
$\Lambda $
-module can be viewed as a representation of the bound quiver
![]() $(Q,I)$
. For the rudiments of representation theory of algebras, we refer to [Reference AuslanderASS].
$(Q,I)$
. For the rudiments of representation theory of algebras, we refer to [Reference AuslanderASS].
1.1 Motivations and background
In 2014, Adachi, Iyama, and Reiten [Reference Assem, Simson and SkowrońskiAIR] introduced
![]() $\tau $
-tilting theory of associative algebras as a modern generalization of classical tilting theory. For an algebra
$\tau $
-tilting theory of associative algebras as a modern generalization of classical tilting theory. For an algebra
![]() $\Lambda $
,
$\Lambda $
,
![]() $\tau $
-tilting theory treats the notion of rigidity and compatibility of
$\tau $
-tilting theory treats the notion of rigidity and compatibility of
![]() $\Lambda $
-modules with respect to the Auslander–Reiten translation
$\Lambda $
-modules with respect to the Auslander–Reiten translation
![]() $\tau _{\Lambda }$
, which we often denote by
$\tau _{\Lambda }$
, which we often denote by
![]() $\tau $
. In particular, the set of (support)
$\tau $
. In particular, the set of (support)
![]() $\tau $
-tilting modules extends that of the classical tilting modules and admits a more consistent behavior with respect to the notion of mutation (see [Reference Assem, Simson and SkowrońskiAIR] for details).
$\tau $
-tilting modules extends that of the classical tilting modules and admits a more consistent behavior with respect to the notion of mutation (see [Reference Assem, Simson and SkowrońskiAIR] for details).
For an algebra
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $\operatorname{\mathrm{tilt}}(\Lambda )$
denote the set of all isomorphism classes of basic tilting modules in
$\operatorname{\mathrm{tilt}}(\Lambda )$
denote the set of all isomorphism classes of basic tilting modules in
![]() $\operatorname{\mathrm{mod}} \Lambda $
. Similarly, by
$\operatorname{\mathrm{mod}} \Lambda $
. Similarly, by
![]() $\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, we denote the set of all basic
$\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, we denote the set of all basic
![]() $\tau $
-tilting modules in
$\tau $
-tilting modules in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphism. Then,
$\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphism. Then,
![]() $\Lambda $
is called tilting-finite if
$\Lambda $
is called tilting-finite if
![]() $|\operatorname{\mathrm{tilt}}(\Lambda )| < \infty $
and it is
$|\operatorname{\mathrm{tilt}}(\Lambda )| < \infty $
and it is
![]() $\tau $
-tilting finite if
$\tau $
-tilting finite if
![]() $|\tau \operatorname{-\textrm{tilt}}(\Lambda )| < \infty $
. As shown in [Reference Assem, Simson and SkowrońskiAIR], (support)
$|\tau \operatorname{-\textrm{tilt}}(\Lambda )| < \infty $
. As shown in [Reference Assem, Simson and SkowrońskiAIR], (support)
![]() $\tau $
-tilting modules closely relate to several fundamental objects in
$\tau $
-tilting modules closely relate to several fundamental objects in
![]() $\operatorname{\mathrm{mod}} \Lambda $
and its bounded derived category. Thus, for a given algebra, it is important to decide whether it is
$\operatorname{\mathrm{mod}} \Lambda $
and its bounded derived category. Thus, for a given algebra, it is important to decide whether it is
![]() $\tau $
-tilting (in)finite. Since
$\tau $
-tilting (in)finite. Since
![]() $\operatorname{\mathrm{tilt}}(\Lambda ) \subseteq \tau \operatorname{-\textrm{tilt}}(\Lambda )$
, each
$\operatorname{\mathrm{tilt}}(\Lambda ) \subseteq \tau \operatorname{-\textrm{tilt}}(\Lambda )$
, each
![]() $\tau $
-tilting finite algebra is evidently tilting-finite, but the converse does not hold in general. For an explicit example, see §4.
$\tau $
-tilting finite algebra is evidently tilting-finite, but the converse does not hold in general. For an explicit example, see §4.
Recall that a module M in
![]() $\operatorname{\mathrm{Ind}}(\Lambda )$
is a brick if
$\operatorname{\mathrm{Ind}}(\Lambda )$
is a brick if
![]() $\operatorname{\mathrm{End}}_{\Lambda }(M)$
is a division algebra. Suppose
$\operatorname{\mathrm{End}}_{\Lambda }(M)$
is a division algebra. Suppose
![]() $\operatorname{\mathrm{Brick}}(\Lambda )$
denotes a collection of all bricks in
$\operatorname{\mathrm{Brick}}(\Lambda )$
denotes a collection of all bricks in
![]() $\operatorname{\mathrm{Mod}} \Lambda $
, up to isomorphism, and similarly,
$\operatorname{\mathrm{Mod}} \Lambda $
, up to isomorphism, and similarly,
![]() $\operatorname{\mathrm{brick}}(\Lambda )$
is a set of all bricks in
$\operatorname{\mathrm{brick}}(\Lambda )$
is a set of all bricks in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphism. In [Reference Demonet, Iyama and JassoDIJ], the authors established the
$\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphism. In [Reference Demonet, Iyama and JassoDIJ], the authors established the
![]() $\tau $
-rigid-brick correspondence, which is an elegant linkage between those indecomposable modules M in
$\tau $
-rigid-brick correspondence, which is an elegant linkage between those indecomposable modules M in
![]() $\operatorname{\mathrm{mod}} \Lambda $
for which
$\operatorname{\mathrm{mod}} \Lambda $
for which
![]() $\operatorname {Hom}_{\Lambda }(M,\tau M)=0$
, and elements of
$\operatorname {Hom}_{\Lambda }(M,\tau M)=0$
, and elements of
![]() $\operatorname{\mathrm{brick}}(\Lambda )$
. Then, they concluded that
$\operatorname{\mathrm{brick}}(\Lambda )$
. Then, they concluded that
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite if and only if
$\tau $
-tilting finite if and only if
![]() $\operatorname{\mathrm{brick}}(\Lambda )$
is finite. More importantly, from [Reference Demonet, Iyama and JassoDIJ], we know that
$\operatorname{\mathrm{brick}}(\Lambda )$
is finite. More importantly, from [Reference Demonet, Iyama and JassoDIJ], we know that
![]() $\tau $
-tilting finite algebras can be viewed as a natural generalization of representation-finite algebras and they admit a phenomenon similar to the finite-type cluster algebras: for
$\tau $
-tilting finite algebras can be viewed as a natural generalization of representation-finite algebras and they admit a phenomenon similar to the finite-type cluster algebras: for
![]() $\Lambda =kQ/I$
with
$\Lambda =kQ/I$
with
![]() $|Q_0|=n$
, each vertex of the mutation graph of support
$|Q_0|=n$
, each vertex of the mutation graph of support
![]() $\tau $
-tilting modules in
$\tau $
-tilting modules in
![]() $\operatorname{\mathrm{mod}} \Lambda $
is n-regular (i.e., each vertex is of degree n) and the graph is finite if and only if
$\operatorname{\mathrm{mod}} \Lambda $
is n-regular (i.e., each vertex is of degree n) and the graph is finite if and only if
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite.
$\tau $
-tilting finite.
Notice that the problem of
![]() $\tau $
-tilting finiteness is of interest only at the level of rep-inf algebras. Therefore, it is natural to treat
$\tau $
-tilting finiteness is of interest only at the level of rep-inf algebras. Therefore, it is natural to treat
![]() $\tau $
-tilting finiteness of those algebras which are rep-inf and minimal with respect to this property. Recall that an algebra
$\tau $
-tilting finiteness of those algebras which are rep-inf and minimal with respect to this property. Recall that an algebra
![]() $\Lambda $
is said to be minimal representation-infinite (min-rep-inf, for short) if
$\Lambda $
is said to be minimal representation-infinite (min-rep-inf, for short) if
![]() $\operatorname{\mathrm{ind}}(\Lambda )$
is infinite, but
$\operatorname{\mathrm{ind}}(\Lambda )$
is infinite, but
![]() $\operatorname{\mathrm{ind}}(\Lambda /J)$
is a finite set, for every nonzero ideal J in
$\operatorname{\mathrm{ind}}(\Lambda /J)$
is a finite set, for every nonzero ideal J in
![]() $\Lambda $
. For any rep-inf algebra
$\Lambda $
. For any rep-inf algebra
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $\operatorname{\mathrm{Mri}}(\Lambda )$
be the set of isomorphism classes of all quotient algebras of
$\operatorname{\mathrm{Mri}}(\Lambda )$
be the set of isomorphism classes of all quotient algebras of
![]() $\Lambda $
that are min-rep-inf. Observe that if there exists
$\Lambda $
that are min-rep-inf. Observe that if there exists
![]() $\Lambda '$
in
$\Lambda '$
in
![]() $\operatorname{\mathrm{Mri}}(\Lambda )$
which is
$\operatorname{\mathrm{Mri}}(\Lambda )$
which is
![]() $\tau $
-tilting infinite, then so is
$\tau $
-tilting infinite, then so is
![]() $\Lambda $
. Thus, it is important to have a description of
$\Lambda $
. Thus, it is important to have a description of
![]() $\tau $
-tilting (in)finiteness of min-rep-inf algebras. This direction of work has been developed by Mousavand [Reference MousavandM1], [Reference MousavandM2]. For further details on this classification, see §2.3.
$\tau $
-tilting (in)finiteness of min-rep-inf algebras. This direction of work has been developed by Mousavand [Reference MousavandM1], [Reference MousavandM2]. For further details on this classification, see §2.3.
Although
![]() $\tau $
-tilting finite algebras have been treated extensively, the study of
$\tau $
-tilting finite algebras have been treated extensively, the study of
![]() $\tau $
-tilting infinite algebras is significantly more complicated. In [Reference Adachi, Iyama and ReitenAY] and [Reference Keller, Plamondon and YurikusaKPY], the authors have studied a family of
$\tau $
-tilting infinite algebras is significantly more complicated. In [Reference Adachi, Iyama and ReitenAY] and [Reference Keller, Plamondon and YurikusaKPY], the authors have studied a family of
![]() $\tau $
-tilting infinite algebras that satisfy some additional properties, called g-tameness. In this work, we have a different perspective and motivated by the following conjecture, and we aim to give a better description of those algebras which are
$\tau $
-tilting infinite algebras that satisfy some additional properties, called g-tameness. In this work, we have a different perspective and motivated by the following conjecture, and we aim to give a better description of those algebras which are
![]() $\tau $
-tilting infinite but minimal with respect to this property. We say
$\tau $
-tilting infinite but minimal with respect to this property. We say
![]() $\Lambda $
is minimal
$\Lambda $
is minimal
![]() $\tau $
-tilting infinite (min-
$\tau $
-tilting infinite (min-
![]() $\tau $
-infinite, for short) if
$\tau $
-infinite, for short) if
![]() $\Lambda $
is a
$\Lambda $
is a
![]() $\tau $
-tilting infinite algebra, but
$\tau $
-tilting infinite algebra, but
![]() $\Lambda /J$
is
$\Lambda /J$
is
![]() $\tau $
-tilting finite, for each nonzero idea J in
$\tau $
-tilting finite, for each nonzero idea J in
![]() $\Lambda $
. As further explained below, min-
$\Lambda $
. As further explained below, min-
![]() $\tau $
-infinite algebras play a crucial role in the study of the following conjecture.
$\tau $
-infinite algebras play a crucial role in the study of the following conjecture.
Conjecture 1.1. If
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting infinite, there exists a positive integer d such that there are infinitely many (non-isomorphic) bricks of length d in
$\tau $
-tilting infinite, there exists a positive integer d such that there are infinitely many (non-isomorphic) bricks of length d in
![]() $\operatorname{\mathrm{mod}} \Lambda $
.
$\operatorname{\mathrm{mod}} \Lambda $
.
The above conjecture can be viewed as a modern analogue of the celebrated Brauer–Thrall conjectures, yet it is not a verbatim counterpart of any of them in terms of bricks. To better clarify this difference, we note that the fundamental theorem of Smalø [Reference SmaløSm] implies the second Brauer–Thrall conjecture: if there is an infinite family of indecomposable modules of length d, there exists a strictly increasing sequence
![]() $d_1< d_2< \cdots $
of integers such that there is an infinite family of indecomposable modules of length
$d_1< d_2< \cdots $
of integers such that there is an infinite family of indecomposable modules of length
![]() $d_i$
, for each i. In contrast, one should not expect an analogue of Smalø’s theorem for bricks. More precisely, the number of integers d in the assertion of Conjecture 1.1 can be finite (in the
$d_i$
, for each i. In contrast, one should not expect an analogue of Smalø’s theorem for bricks. More precisely, the number of integers d in the assertion of Conjecture 1.1 can be finite (in the
![]() $2$
-Kronecker algebra, there is exactly one such d). As an immediate consequence of Smalø’s theorem, Conjecture 1.1 implies the second Brauer–Thrall conjecture.
$2$
-Kronecker algebra, there is exactly one such d). As an immediate consequence of Smalø’s theorem, Conjecture 1.1 implies the second Brauer–Thrall conjecture.
Adopting a different perspective while treating Conjecture 1.1 allows us to better manifest the analogy between the classical and new settings. In particular, we remark that Crawley-Boevey [Reference Crawley-BoeveyC] has shown that
![]() $\Lambda $
is rep-inf if and only if for some d, there are infinitely many (non-isomorphic) modules in
$\Lambda $
is rep-inf if and only if for some d, there are infinitely many (non-isomorphic) modules in
![]() $\operatorname{\mathrm{ind}}(\Lambda )$
of endolength d. From this viewpoint, Conjecture 1.1 is the analogous assertion for bricks:
$\operatorname{\mathrm{ind}}(\Lambda )$
of endolength d. From this viewpoint, Conjecture 1.1 is the analogous assertion for bricks:
![]() $\Lambda $
is brick-infinite if and only if for some d, there are infinitely many (non-isomorphic) modules in
$\Lambda $
is brick-infinite if and only if for some d, there are infinitely many (non-isomorphic) modules in
![]() $\operatorname{\mathrm{brick}}(A)$
of (endo)length d.
$\operatorname{\mathrm{brick}}(A)$
of (endo)length d.
To prove Conjecture 1.1 in full generality, observe that it suffices to show it for all min-
![]() $\tau $
-infinite algebras. This conjecture first appeared in [Reference MousavandM2], where Mousavand phrased it in a more geometric language to establish a new linkage between
$\tau $
-infinite algebras. This conjecture first appeared in [Reference MousavandM2], where Mousavand phrased it in a more geometric language to establish a new linkage between
![]() $\tau $
-tilting theory and geometry of representation varieties of quivers. Furthermore, in the aforementioned paper, the conjecture was verified for gentle algebras, as well as all the min-rep-inf algebras treated there. In [Reference Schroll, Treffinger and ValdiviesoSTV], the authors have also come across the same conjecture and verified it for special biserial algebras.
$\tau $
-tilting theory and geometry of representation varieties of quivers. Furthermore, in the aforementioned paper, the conjecture was verified for gentle algebras, as well as all the min-rep-inf algebras treated there. In [Reference Schroll, Treffinger and ValdiviesoSTV], the authors have also come across the same conjecture and verified it for special biserial algebras.
1.2 Outline and main results
In §2, we introduce our notations and terminology. Furthermore, we collect some known results essential in our work. Before we state our main results, let us give analogous characterizations of the classical and modern minimality conditions discussed in §2. The following statements follow from a known result of Auslander [Reference Aihara and IyamaAu] and the recent work of Sentieri [Reference SentieriSe]. In particular, for an algebra
![]() $\Lambda $
, we have:
$\Lambda $
, we have:
-
•
 $\Lambda $
is min-rep-inf if and only if
$\Lambda $
is min-rep-inf if and only if
 $\operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )\neq \emptyset $
and every
$\operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )\neq \emptyset $
and every
 $M \in \operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
is faithful.
$M \in \operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
is faithful. -
•
 $\Lambda $
is min-
$\Lambda $
is min-
 $\tau $
-infinite if and only if
$\tau $
-infinite if and only if
 $\operatorname{\mathrm{Brick}}(\Lambda )\setminus \operatorname{\mathrm{brick}}(\Lambda )\neq \emptyset $
and every
$\operatorname{\mathrm{Brick}}(\Lambda )\setminus \operatorname{\mathrm{brick}}(\Lambda )\neq \emptyset $
and every
 $N \in \operatorname{\mathrm{Brick}}(\Lambda )\setminus \operatorname{\mathrm{brick}}(\Lambda )$
is faithful.
$N \in \operatorname{\mathrm{Brick}}(\Lambda )\setminus \operatorname{\mathrm{brick}}(\Lambda )$
is faithful.
The next theorem lists some important properties of min-
![]() $\tau $
-infinite algebras, which are shown in propositions 3.1, 3.2, and 3.5. As explained in §3, this theorem also highlights some fundamental differences and similarities between the min-
$\tau $
-infinite algebras, which are shown in propositions 3.1, 3.2, and 3.5. As explained in §3, this theorem also highlights some fundamental differences and similarities between the min-
![]() $\tau $
-infinite algebras and the min-rep-inf algebras.
$\tau $
-infinite algebras and the min-rep-inf algebras.
Theorem 1.1. Let
![]() $\Lambda =kQ/I$
be a min-
$\Lambda =kQ/I$
be a min-
![]() $\tau $
-infinite algebra. Then
$\tau $
-infinite algebra. Then
![]() $\Lambda $
is node-free and central. Moreover,
$\Lambda $
is node-free and central. Moreover,
![]() $\Lambda $
admits no projective-injective module.
$\Lambda $
admits no projective-injective module.
The previous theorem leads to the following classification result on algebras with radical square zero, from which one immediately verifies Conjecture 1.1 for such algebras. This also gives a simple proof for the following result of Adachi [Reference AdachiAd]. We say Q is a sink-source quiver if every vertex of Q is either a sink or a source.
Corollary 1.2 [Reference AdachiAd]
Let
![]() $\Lambda =kQ/I$
be such that
$\Lambda =kQ/I$
be such that
![]() $\operatorname{\mathrm{rad}}^2(\Lambda )=0$
. The following are equivalent:
$\operatorname{\mathrm{rad}}^2(\Lambda )=0$
. The following are equivalent:
-
1.
 $\Lambda $
is
$\Lambda $
is
 $\tau $
-tilting infinite.
$\tau $
-tilting infinite. -
2. Q contains a sink-source subquiver of affine type.
In §4, we slightly change our perspective and study the min-
![]() $\tau $
-infinite algebras from the viewpoint of classical tilting theory. More specifically, we prove that min-
$\tau $
-infinite algebras from the viewpoint of classical tilting theory. More specifically, we prove that min-
![]() $\tau $
-infinite algebras are in fact minimal with respect to the notion of tilting modules, where the minimality is defined analogously: an algebra
$\tau $
-infinite algebras are in fact minimal with respect to the notion of tilting modules, where the minimality is defined analogously: an algebra
![]() $\Lambda $
is min-
tilting
-infinite if it admits infinitely many tilting modules, but every proper quotient algebra
$\Lambda $
is min-
tilting
-infinite if it admits infinitely many tilting modules, but every proper quotient algebra
![]() $\Lambda /J$
has only finitely many tilting modules.
$\Lambda /J$
has only finitely many tilting modules.
Before we summarize the main results of §4 in the following theorem, let us recall that for a collection of objects
![]() $\mathfrak {O}$
, we say almost all objects of
$\mathfrak {O}$
, we say almost all objects of
![]() $\mathfrak {O}$
satisfy property
$\mathfrak {O}$
satisfy property
![]() $\mathcal {P}$
provided all but finitely many objects of
$\mathcal {P}$
provided all but finitely many objects of
![]() $\mathfrak {O}$
have property
$\mathfrak {O}$
have property
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Theorem 1.3. Let
![]() $\Lambda $
be an algebra. If
$\Lambda $
be an algebra. If
![]() $\Lambda $
is min-
$\Lambda $
is min-
![]() $\tau $
-infinite, then almost all
$\tau $
-infinite, then almost all
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $\Lambda $
-modules are partial tilting. Consequently, we have:
$\Lambda $
-modules are partial tilting. Consequently, we have:
-
1.
 $\Lambda $
is min-
$\Lambda $
is min-
 $\tau $
-infinite if and only if it is minimal tilting infinite.
$\tau $
-infinite if and only if it is minimal tilting infinite. -
2. If
 $\Lambda $
is min-
$\Lambda $
is min-
 $\tau $
-infinite, then the mutation graph of tilting modules in
$\tau $
-infinite, then the mutation graph of tilting modules in
 $\operatorname{\mathrm{mod}} \Lambda $
is infinite and regular at almost every vertex.
$\operatorname{\mathrm{mod}} \Lambda $
is infinite and regular at almost every vertex.
In §5, we use min-
![]() $\tau $
-infinite algebras in the study of Conjecture 1.1. Before we state the next theorem, we note that a min-
$\tau $
-infinite algebras in the study of Conjecture 1.1. Before we state the next theorem, we note that a min-
![]() $\tau $
-infinite algebra may admit infinitely many non-isomorphic bricks with distinct annihilators. However, we prove that it is sufficient to only treat the conjecture for a particular subfamily of min-
$\tau $
-infinite algebra may admit infinitely many non-isomorphic bricks with distinct annihilators. However, we prove that it is sufficient to only treat the conjecture for a particular subfamily of min-
![]() $\tau $
-infinite algebras, as stated in the following theorem.
$\tau $
-infinite algebras, as stated in the following theorem.
Theorem 1.4. To verify Conjecture 1.1, it is sufficient to consider min-
![]() $\tau $
-infinite algebras for which almost all bricks are faithful.
$\tau $
-infinite algebras for which almost all bricks are faithful.
Finally, in §6, we employ some tools from the algebro-geometric aspects of representation theory of algebras to show the following result on the minimal extending bricks (for the definition, see §5). As an immediate consequence of this theorem, we give a simple proof of the modern analogue of the first Brauer–Thrall conjecture, first shown in [Reference Schroll and TreffingerST] over an arbitrary field.
Theorem 1.5. Let
![]() $\Lambda $
be an algebra, and let M be a minimal extending brick in
$\Lambda $
be an algebra, and let M be a minimal extending brick in
![]() $\operatorname{\mathrm{mod}} \Lambda $
with dimensional vector
$\operatorname{\mathrm{mod}} \Lambda $
with dimensional vector
![]() $\mathbf {d}$
. Then, the orbit of M under the
$\mathbf {d}$
. Then, the orbit of M under the
![]() $\operatorname{\mathrm{GL}}(\mathbf {d})$
action is open.
$\operatorname{\mathrm{GL}}(\mathbf {d})$
action is open.
As mentioned before, our work is primarily motivated by Conjecture 1.1 and some of our main arguments rely on the study of bricks. Nevertheless, we stated our results in terms of
![]() $\tau $
-tilting (in)finiteness of algebras under consideration. This allows us to better relate our study to the other subjects discussed in the paper.
$\tau $
-tilting (in)finiteness of algebras under consideration. This allows us to better relate our study to the other subjects discussed in the paper.
2 Preliminaries
In this section, we only collect some basic materials needed in the rest of the paper. The well-known results appear without proofs but only references, if necessary.
2.1 Notations and conventions
In addition to those introduced in §1, here we fix some notations and conventions used throughout the paper.
By a quiver, we always mean a finite directed graph, formally given by a quadruple
![]() $Q=(Q_0,Q_1,s,e)$
, with the vertex set
$Q=(Q_0,Q_1,s,e)$
, with the vertex set
![]() $Q_0$
and arrow set
$Q_0$
and arrow set
![]() $Q_1$
, and the functions
$Q_1$
, and the functions
![]() $s,e: Q_1 \rightarrow Q_0$
, respectively, send each arrow
$s,e: Q_1 \rightarrow Q_0$
, respectively, send each arrow
![]() $\alpha $
to its start
$\alpha $
to its start
![]() $s(\alpha )$
and its end
$s(\alpha )$
and its end
![]() $e(\alpha )$
. As mentioned before, up to Morita equivalence, every algebra
$e(\alpha )$
. As mentioned before, up to Morita equivalence, every algebra
![]() $\Lambda $
treated in this paper is of the form
$\Lambda $
treated in this paper is of the form
![]() $\Lambda =kQ/I$
, for a unique quiver Q and an admissible ideal I in
$\Lambda =kQ/I$
, for a unique quiver Q and an admissible ideal I in
![]() $kQ$
. In particular,
$kQ$
. In particular,
![]() $|K_0(\Lambda )|=|Q_0|$
, where
$|K_0(\Lambda )|=|Q_0|$
, where
![]() $|Q_0|$
is the number of vertices of Q. In a bound quiver
$|Q_0|$
is the number of vertices of Q. In a bound quiver
![]() $(Q,I)$
, if the arrow
$(Q,I)$
, if the arrow
![]() $\alpha $
ends where the arrow
$\alpha $
ends where the arrow
![]() $\beta $
starts, then
$\beta $
starts, then
![]() $\beta \alpha $
denotes the path of length 2 in Q. Moreover, a vertex v in
$\beta \alpha $
denotes the path of length 2 in Q. Moreover, a vertex v in
![]() $(Q,I)$
is called a node if it is neither a sink nor a source, and for each pair of arrows
$(Q,I)$
is called a node if it is neither a sink nor a source, and for each pair of arrows
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in Q with
$\beta $
in Q with
![]() $e(\alpha )=v=s(\beta )$
, we have
$e(\alpha )=v=s(\beta )$
, we have
![]() $\beta \alpha \in I$
. Then,
$\beta \alpha \in I$
. Then,
![]() $\Lambda =kQ/I$
is called node-free if
$\Lambda =kQ/I$
is called node-free if
![]() $(Q,I)$
has no nodes.
$(Q,I)$
has no nodes.
If
![]() $\Lambda =kQ/I$
, by R, we denote a minimal set of (uniform) relations that generates I. Namely, each element of R is a linear combination of the form
$\Lambda =kQ/I$
, by R, we denote a minimal set of (uniform) relations that generates I. Namely, each element of R is a linear combination of the form
![]() $r=\sum _{i=1}^{t} \lambda _i p_i$
, with
$r=\sum _{i=1}^{t} \lambda _i p_i$
, with
![]() $t\in \mathbb {Z}_{>0}$
and
$t\in \mathbb {Z}_{>0}$
and
![]() $\lambda _i \in k\setminus \{0\}$
, and every
$\lambda _i \in k\setminus \{0\}$
, and every
![]() $p_i$
is a path in Q whose length is not smaller than 2, and all
$p_i$
is a path in Q whose length is not smaller than 2, and all
![]() $p_i$
start at the same vertex and also end at the same vertex. The relation r is monomial if
$p_i$
start at the same vertex and also end at the same vertex. The relation r is monomial if
![]() $t=1$
, and is called binomial if
$t=1$
, and is called binomial if
![]() $t=2$
.
$t=2$
.
For any algebra
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
denote the set of all (two-sided) ideals in
$\operatorname{\mathrm{Ideal}}(\Lambda )$
denote the set of all (two-sided) ideals in
![]() $\Lambda $
. Note that
$\Lambda $
. Note that
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
carries a natural lattice structure, where
$\operatorname{\mathrm{Ideal}}(\Lambda )$
carries a natural lattice structure, where
![]() $J_1 \wedge J_2:=J_1 \cap J_2$
and
$J_1 \wedge J_2:=J_1 \cap J_2$
and
![]() $J_1 \vee J_2:=J_1 + J_2$
, for each pair
$J_1 \vee J_2:=J_1 + J_2$
, for each pair
![]() $J_1$
and
$J_1$
and
![]() $J_2$
in
$J_2$
in
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
. Consequently,
$\operatorname{\mathrm{Ideal}}(\Lambda )$
. Consequently,
![]() $\Lambda $
is called distributive if
$\Lambda $
is called distributive if
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
is a distributive lattice. Otherwise,
$\operatorname{\mathrm{Ideal}}(\Lambda )$
is a distributive lattice. Otherwise,
![]() $\Lambda $
is non-distributive. From [Reference JansJ1, Cor. 3.1], we know that
$\Lambda $
is non-distributive. From [Reference JansJ1, Cor. 3.1], we know that
![]() $\Lambda $
is distributive if and only if
$\Lambda $
is distributive if and only if
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
is finite. Moreover, it is immediate that every quotient of a distributive algebra is again distributive. Moreover, it is known that each nondistributive algebra is rep-inf. We also recall that a k-algebra is said to be central if
$\operatorname{\mathrm{Ideal}}(\Lambda )$
is finite. Moreover, it is immediate that every quotient of a distributive algebra is again distributive. Moreover, it is known that each nondistributive algebra is rep-inf. We also recall that a k-algebra is said to be central if
![]() $Z(\Lambda )=k$
, where
$Z(\Lambda )=k$
, where
![]() $Z(\Lambda )$
denotes the center of
$Z(\Lambda )$
denotes the center of
![]() $\Lambda $
.
$\Lambda $
.
For X in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, let
$\operatorname{\mathrm{mod}} \Lambda $
, let
![]() $|X|$
denote the number of non-isomorphic indecomposable summands of X. Then, X is basic if
$|X|$
denote the number of non-isomorphic indecomposable summands of X. Then, X is basic if
![]() $|X|$
is exactly the same as the number of indecomposable summands of X. Moreover, by
$|X|$
is exactly the same as the number of indecomposable summands of X. Moreover, by
![]() $\operatorname{\mathrm{pd}}_{\Lambda }(X)$
and
$\operatorname{\mathrm{pd}}_{\Lambda }(X)$
and
![]() $\tau _{\Lambda }X$
, we, respectively, denote the projective dimension and the Auslander–Reiten translation of X in
$\tau _{\Lambda }X$
, we, respectively, denote the projective dimension and the Auslander–Reiten translation of X in
![]() $\operatorname{\mathrm{mod}} \Lambda $
. If there is no confusion,
$\operatorname{\mathrm{mod}} \Lambda $
. If there is no confusion,
![]() $\Lambda $
is often suppressed from our notations. The support of X at vertex
$\Lambda $
is often suppressed from our notations. The support of X at vertex
![]() $i\in Q_0$
is defined as
$i\in Q_0$
is defined as
![]() $X_i:=\operatorname {Hom}_{\Lambda }(P_i,X)$
, and the dimension vector of X is
$X_i:=\operatorname {Hom}_{\Lambda }(P_i,X)$
, and the dimension vector of X is
![]() $\underline {\dim }(X)=(\dim X_i)_{i\in Q_0}$
. Then, X is sincere if
$\underline {\dim }(X)=(\dim X_i)_{i\in Q_0}$
. Then, X is sincere if
![]() $\underline {\dim }(X) \in \mathbb {Z}^{Q_0}_{>0}$
.
$\underline {\dim }(X) \in \mathbb {Z}^{Q_0}_{>0}$
.
An algebra
![]() $\Lambda $
is biserial if for every left and right indecomposable projective
$\Lambda $
is biserial if for every left and right indecomposable projective
![]() $\Lambda $
-module P, the submodule
$\Lambda $
-module P, the submodule
![]() $\operatorname{\mathrm{rad}}(P)$
is sum of at most two uniserial modules X and Y and
$\operatorname{\mathrm{rad}}(P)$
is sum of at most two uniserial modules X and Y and
![]() $X \cap Y$
is either zero or a simple module. Moreover,
$X \cap Y$
is either zero or a simple module. Moreover,
![]() $\Lambda $
is special biserial if it is Morita-equivalent to an algebra
$\Lambda $
is special biserial if it is Morita-equivalent to an algebra
![]() $kQ/I$
such that
$kQ/I$
such that
![]() $(Q,I)$
satisfies the following:
$(Q,I)$
satisfies the following:
-
(B1) At every vertex x in Q, there are at most two incoming and at most two outgoing arrows.
-
(B2) For each arrow
 $\alpha $
, there is at most one arrow
$\alpha $
, there is at most one arrow
 $\beta $
such that
$\beta $
such that
 $\beta \alpha \notin I$
and at most one arrow
$\beta \alpha \notin I$
and at most one arrow
 $\gamma $
such that
$\gamma $
such that
 $\alpha \gamma \notin I$
.
$\alpha \gamma \notin I$
.
We note that every special biserial algebra is biserial, but the converse is not true. Furthermore, for each special biserial algebra
![]() $\Lambda =kQ/I$
, one can choose a minimal set of generators for I consisting of only monomial and binomial relations. A special biserial algebra
$\Lambda =kQ/I$
, one can choose a minimal set of generators for I consisting of only monomial and binomial relations. A special biserial algebra
![]() $\Lambda =kQ/I$
is said to be a string algebra if there is a set of monomial relations in
$\Lambda =kQ/I$
is said to be a string algebra if there is a set of monomial relations in
![]() $kQ$
which generate I.
$kQ$
which generate I.
By a subcategory of
![]() $\operatorname{\mathrm{Mod}} \Lambda $
, we always mean a full subcategory which is closed under direct sum, direct summands, and isomorphisms. A subcategory
$\operatorname{\mathrm{Mod}} \Lambda $
, we always mean a full subcategory which is closed under direct sum, direct summands, and isomorphisms. A subcategory
![]() $\mathcal {T}$
of
$\mathcal {T}$
of
![]() $\operatorname{\mathrm{mod}} \Lambda $
is a torsion class if it is closed under quotients and extensions. Dually, a subcategory
$\operatorname{\mathrm{mod}} \Lambda $
is a torsion class if it is closed under quotients and extensions. Dually, a subcategory
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\operatorname{\mathrm{mod}} \Lambda $
is torsion-free if
$\operatorname{\mathrm{mod}} \Lambda $
is torsion-free if
![]() $\mathcal {F}$
is closed under submodules and extensions. It is well known that every torsion class
$\mathcal {F}$
is closed under submodules and extensions. It is well known that every torsion class
![]() $\mathcal {T}$
uniquely determines a torsion pair
$\mathcal {T}$
uniquely determines a torsion pair
![]() $(\mathcal {T}, \mathcal {F})$
in
$(\mathcal {T}, \mathcal {F})$
in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, where for each
$\operatorname{\mathrm{mod}} \Lambda $
, where for each
![]() $X \in \mathcal {T}$
and every
$X \in \mathcal {T}$
and every
![]() $Y \in \mathcal {F}$
, we have
$Y \in \mathcal {F}$
, we have
![]() $\operatorname {Hom}_{\Lambda }(X,Y)=0$
, and
$\operatorname {Hom}_{\Lambda }(X,Y)=0$
, and
![]() $\mathcal {F}$
is maximal with this property.
$\mathcal {F}$
is maximal with this property.
2.2
 $\tau $
-tilting finite algebras
$\tau $
-tilting finite algebras
A
![]() $\Lambda $
-module M is called rigid if
$\Lambda $
-module M is called rigid if
![]() $\operatorname {Ext}^1_{\Lambda }(M,M)=0$
. By
$\operatorname {Ext}^1_{\Lambda }(M,M)=0$
. By
![]() $\operatorname{\mathrm{rigid}} (\Lambda )$
, we denote the set of all basic rigid objects in
$\operatorname{\mathrm{rigid}} (\Lambda )$
, we denote the set of all basic rigid objects in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, considered up to isomorphisms. Similarly, M is said to be
$\operatorname{\mathrm{mod}} \Lambda $
, considered up to isomorphisms. Similarly, M is said to be
![]() $\tau $
-rigid if
$\tau $
-rigid if
![]() $\operatorname {Hom}_{\Lambda }(M,\tau M)=0$
. Analogously, we use
$\operatorname {Hom}_{\Lambda }(M,\tau M)=0$
. Analogously, we use
![]() $\tau \operatorname{-\textrm{rigid}}(\Lambda )$
to denote the set of basic
$\tau \operatorname{-\textrm{rigid}}(\Lambda )$
to denote the set of basic
![]() $\tau $
-rigid modules in
$\tau $
-rigid modules in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphisms. A rigid module X is called tilting if
$\operatorname{\mathrm{mod}} \Lambda $
, up to isomorphisms. A rigid module X is called tilting if
![]() $\operatorname{\mathrm{pd}}_{\Lambda }\leq 1$
and
$\operatorname{\mathrm{pd}}_{\Lambda }\leq 1$
and
![]() $|X|=|\Lambda |$
. Similarly, each
$|X|=|\Lambda |$
. Similarly, each
![]() $\tau $
-rigid module M with
$\tau $
-rigid module M with
![]() $|M|=|\Lambda |$
is said to be
$|M|=|\Lambda |$
is said to be
![]() $\tau $
-tilting. More generally, M is called support
$\tau $
-tilting. More generally, M is called support
![]() $\tau $
-tilting if M is
$\tau $
-tilting if M is
![]() $\tau $
-tilting over
$\tau $
-tilting over
![]() $\Lambda /\langle e \rangle $
, where e is a maximal idempotent in
$\Lambda /\langle e \rangle $
, where e is a maximal idempotent in
![]() $\operatorname{\mathrm{ann}}_{\Lambda }(M)$
. By
$\operatorname{\mathrm{ann}}_{\Lambda }(M)$
. By
![]() $\tau \operatorname{-\textrm{tilt}}(\Lambda )$
and
$\tau \operatorname{-\textrm{tilt}}(\Lambda )$
and
![]() $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, we, respectively, denote the set of basic
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, we, respectively, denote the set of basic
![]() $\tau $
-tilting modules and that of basic support
$\tau $
-tilting modules and that of basic support
![]() $\tau $
-tilting modules in
$\tau $
-tilting modules in
![]() $\operatorname{\mathrm{mod}} \Lambda $
, considered up to isomorphisms.
$\operatorname{\mathrm{mod}} \Lambda $
, considered up to isomorphisms.
Recently, there have been various attempts to systematically study the
![]() $\tau $
-tilting finiteness of algebras. That is to find the necessary and sufficient conditions for arbitrary algebra
$\tau $
-tilting finiteness of algebras. That is to find the necessary and sufficient conditions for arbitrary algebra
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $|\tau \operatorname{-\textrm{tilt}}(\Lambda )| < \infty $
. The brick-
$|\tau \operatorname{-\textrm{tilt}}(\Lambda )| < \infty $
. The brick-
![]() $\tau $
-rigid correspondence introduced by Demonet, Iyama, and Jasso [Reference Demonet, Iyama and JassoDIJ] was a significant step toward such an objective. The following theorem collects some fundamental characterizations of
$\tau $
-rigid correspondence introduced by Demonet, Iyama, and Jasso [Reference Demonet, Iyama and JassoDIJ] was a significant step toward such an objective. The following theorem collects some fundamental characterizations of
![]() $\tau $
-tilting finite algebras extensively used in this paper.
$\tau $
-tilting finite algebras extensively used in this paper.
Theorem 2.1 [Reference Assem, Simson and SkowrońskiAIR, Reference Demonet, Iyama and JassoDIJ]
For an algebra
![]() $\Lambda $
, the following are equivalent:
$\Lambda $
, the following are equivalent:
-
1.
 $\Lambda $
is
$\Lambda $
is
 $\tau $
-tilting finite.
$\tau $
-tilting finite. -
2.
 $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
is finite.
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
is finite. -
3.
 $\tau \operatorname{\mathrm{rigid}}(\Lambda )$
is finite.
$\tau \operatorname{\mathrm{rigid}}(\Lambda )$
is finite. -
4.
 $\operatorname{\mathrm{mod}} \Lambda $
contains only finitely many isomorphism classes of bricks.
$\operatorname{\mathrm{mod}} \Lambda $
contains only finitely many isomorphism classes of bricks. -
5. Every torsion(-free) class in
 $\operatorname{\mathrm{mod}} \Lambda $
is functorially finite.
$\operatorname{\mathrm{mod}} \Lambda $
is functorially finite.
2.3 Minimality conditions
Before we review some minimality conditions, let us make a handy observation that will be freely used throughout our work.
We recall that any epimorphism of algebras
![]() $\psi : \Lambda _1 \rightarrow \Lambda _2$
induces an exact functorial embedding
$\psi : \Lambda _1 \rightarrow \Lambda _2$
induces an exact functorial embedding
![]() $\widetilde {\psi }: \operatorname{\mathrm{mod}}\Lambda _2 \rightarrow \operatorname{\mathrm{mod}}\Lambda _1$
. In particular, every indecomposable (resp. brick) in
$\widetilde {\psi }: \operatorname{\mathrm{mod}}\Lambda _2 \rightarrow \operatorname{\mathrm{mod}}\Lambda _1$
. In particular, every indecomposable (resp. brick) in
![]() $\operatorname{\mathrm{mod}} \Lambda _2$
can be seen as an indecomposable (resp. brick) in
$\operatorname{\mathrm{mod}} \Lambda _2$
can be seen as an indecomposable (resp. brick) in
![]() $\operatorname{\mathrm{mod}} \Lambda _1$
. Hence, representation finiteness of algebras is preserved under algebraic quotients: if
$\operatorname{\mathrm{mod}} \Lambda _1$
. Hence, representation finiteness of algebras is preserved under algebraic quotients: if
![]() $\Lambda $
is rep-finite, then
$\Lambda $
is rep-finite, then
![]() $\Lambda /J$
is rep-finite, for each J in
$\Lambda /J$
is rep-finite, for each J in
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
. Moreover, by Theorem 2.1, it is immediate that the
$\operatorname{\mathrm{Ideal}}(\Lambda )$
. Moreover, by Theorem 2.1, it is immediate that the
![]() $\tau $
-tilting finiteness of algebras is also preserved under taking quotients. In contrast, we note that there are tilting finite algebras
$\tau $
-tilting finiteness of algebras is also preserved under taking quotients. In contrast, we note that there are tilting finite algebras
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\Lambda /J$
is tilting infinite, for some
$\Lambda /J$
is tilting infinite, for some
![]() $J \in \operatorname{\mathrm{Ideal}} (\Lambda )$
.
$J \in \operatorname{\mathrm{Ideal}} (\Lambda )$
.
Due to the above observation, rep-inf algebras which are minimal with respect to this property have been decisive in the study of representation theory of algebras, such as in the proofs of Brauer–Thrall conjectures. As defined earlier,
![]() $\Lambda $
is min-rep-inf if it is rep-inf, but any proper quotient of
$\Lambda $
is min-rep-inf if it is rep-inf, but any proper quotient of
![]() $\Lambda $
is representation-finite. The literature on min-rep-inf algebras is very rich (see, e.g., [Reference Barnard, Carroll and ZhuBo1], [Reference BongartzBo2] and the references therein). Notice that the latter two works of Bongartz also account for the decisive role of min-rep-inf algebras in the study of the Brauer–Thrall conjectures. A conceptual classification of these algebras appears in [Reference RingelR], where Ringel shows that each min-rep-inf algebra belongs to at least one of the following families. For the definition of a good covering, see [Reference Barnard, Carroll and ZhuBo1].
$\Lambda $
is representation-finite. The literature on min-rep-inf algebras is very rich (see, e.g., [Reference Barnard, Carroll and ZhuBo1], [Reference BongartzBo2] and the references therein). Notice that the latter two works of Bongartz also account for the decisive role of min-rep-inf algebras in the study of the Brauer–Thrall conjectures. A conceptual classification of these algebras appears in [Reference RingelR], where Ringel shows that each min-rep-inf algebra belongs to at least one of the following families. For the definition of a good covering, see [Reference Barnard, Carroll and ZhuBo1].
-
•
 $\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{sB}}}})$
: min-rep-inf special Biserial algebras;
$\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{sB}}}})$
: min-rep-inf special Biserial algebras; -
•
 $\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{nD}}}})$
: min-rep-inf non-Distributive algebras;
$\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{nD}}}})$
: min-rep-inf non-Distributive algebras; -
•
 $\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{gC}}}})$
: min-rep-inf algebras with a good Covering
$\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{gC}}}})$
: min-rep-inf algebras with a good Covering
 $\widetilde {\Lambda }$
such that a finite convex subcategory of
$\widetilde {\Lambda }$
such that a finite convex subcategory of
 $\widetilde {\Lambda }$
is tame-concealed of type
$\widetilde {\Lambda }$
is tame-concealed of type
 $\widetilde {\mathbb {D}}_n$
or
$\widetilde {\mathbb {D}}_n$
or
 $\widetilde {\mathbb {E}}_{6,7,8}$
.
$\widetilde {\mathbb {E}}_{6,7,8}$
.
The bound quivers of the first two subfamilies from the above list are, respectively, described in [Reference BongartzBo2] and [Reference RingelR]. Moreover, it is known that a concrete classification of the last subfamily in terms of their bound quivers is very hard, if not impossible, and soon falls out of control as the number of simple modules grows.
As of a more contemporary approach to the study of min-rep-inf algebras, it is natural to determine which ones are
![]() $\tau $
-tilting (in)finite. One can show that each of the above-mentioned subfamilies contains both
$\tau $
-tilting (in)finite. One can show that each of the above-mentioned subfamilies contains both
![]() $\tau $
-tilting finite and
$\tau $
-tilting finite and
![]() $\tau $
-tilting infinite algebras. In [Reference MousavandM1] and [Reference MousavandM2], Mousavand carried out a full study of
$\tau $
-tilting infinite algebras. In [Reference MousavandM1] and [Reference MousavandM2], Mousavand carried out a full study of
![]() $\tau $
-tilting finiteness of the algebras in
$\tau $
-tilting finiteness of the algebras in
![]() $\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{sB}}}})$
and
$\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{sB}}}})$
and
![]() $\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{nD}}}})$
and determined which ones are
$\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{nD}}}})$
and determined which ones are
![]() $\tau $
-tilting finite and which ones are not. The following theorem captures the main results in this direction. For explicit description of the bound quivers and further details, see the aforementioned papers.
$\tau $
-tilting finite and which ones are not. The following theorem captures the main results in this direction. For explicit description of the bound quivers and further details, see the aforementioned papers.
Theorem 2.2 [Reference MousavandM2]
Let
![]() $\Lambda = kQ/I$
belong to
$\Lambda = kQ/I$
belong to
![]() $\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{sB}}}}) \cup \operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{nD}}}})$
. Then
$\operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{sB}}}}) \cup \operatorname{\mathrm{Mri}}({\mathfrak {F}_{\operatorname{\mathrm{nD}}}})$
. Then
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite if and only if
$\tau $
-tilting finite if and only if
![]() $(Q,I)$
has a node or a nonquadratic monomial relation.
$(Q,I)$
has a node or a nonquadratic monomial relation.
3 Minimal
 $\tau $
-tilting infinite algebras
$\tau $
-tilting infinite algebras
As already noticed,
![]() $\tau $
-tilting finiteness of algebras is preserved under taking algebraic quotients. In [Reference MousavandM1] and [Reference WangW], where the problem of
$\tau $
-tilting finiteness of algebras is preserved under taking algebraic quotients. In [Reference MousavandM1] and [Reference WangW], where the problem of
![]() $\tau $
-tilting finiteness is concerned, the authors independently noticed that a natural analogue of min-rep-inf algebras in the modern setting should be crucial in the study of
$\tau $
-tilting finiteness is concerned, the authors independently noticed that a natural analogue of min-rep-inf algebras in the modern setting should be crucial in the study of
![]() $\tau $
-tilting (in)finiteness. In particular, an algebra
$\tau $
-tilting (in)finiteness. In particular, an algebra
![]() $\Lambda $
is min-
$\Lambda $
is min-
![]() $\tau $
-infinite, if
$\tau $
-infinite, if
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting infinite, but every proper quotient algebra of
$\tau $
-tilting infinite, but every proper quotient algebra of
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite.
$\tau $
-tilting finite.
Inspired by the classification of min-rep-inf algebras, as briefly recalled in §2.3, it is natural to search for a classification of min-
![]() $\tau $
-infinite algebras. Although it might be impossible to describe the bound quivers of all of min-
$\tau $
-infinite algebras. Although it might be impossible to describe the bound quivers of all of min-
![]() $\tau $
-infinite algebras, one can still treat this problem for certain subfamilies of them. We pursue this direction of work in a separate paper. In this section, we focus on some fundamental properties of min-
$\tau $
-infinite algebras, one can still treat this problem for certain subfamilies of them. We pursue this direction of work in a separate paper. In this section, we focus on some fundamental properties of min-
![]() $\tau $
-infinite algebras. In particular, we compare min-rep-inf and min-
$\tau $
-infinite algebras. In particular, we compare min-rep-inf and min-
![]() $\tau $
-infinite algebras and derive some interesting results from this comparison.
$\tau $
-infinite algebras and derive some interesting results from this comparison.
It is known that a min-rep-inf algebra admits no projective-injective module. Let us begin by showing that the same property holds for min-
![]() $\tau $
-infinite algebras. For the sake of brevity, for two algebras
$\tau $
-infinite algebras. For the sake of brevity, for two algebras
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
, we say
$\Lambda _2$
, we say
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
are of the same
$\Lambda _2$
are of the same
![]() $\tau $
-tilting type when
$\tau $
-tilting type when
![]() $\Lambda _1$
is
$\Lambda _1$
is
![]() $\tau $
-tilting finite if and only if
$\tau $
-tilting finite if and only if
![]() $\Lambda _2$
is so.
$\Lambda _2$
is so.
Proposition 3.1. Let
![]() $\Lambda $
be an algebra such that
$\Lambda $
be an algebra such that
![]() $\operatorname{\mathrm{mod}} \Lambda $
contains a projective-injective module. Then, there exists a nonzero ideal J such that
$\operatorname{\mathrm{mod}} \Lambda $
contains a projective-injective module. Then, there exists a nonzero ideal J such that
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda /J$
are of the same
$\Lambda /J$
are of the same
![]() $\tau $
-tilting type. Consequently, if
$\tau $
-tilting type. Consequently, if
![]() $\Lambda $
is min-
$\Lambda $
is min-
![]() $\tau $
-infinite, there is no projective-injective module in
$\tau $
-infinite, there is no projective-injective module in
![]() $\operatorname{\mathrm{mod}} \Lambda $
.
$\operatorname{\mathrm{mod}} \Lambda $
.
Proof. Suppose
![]() $\Lambda =kQ/I$
, and let
$\Lambda =kQ/I$
, and let
![]() $X \in \operatorname{\mathrm{ind}}(\Lambda )$
be projective-injective. Then,
$X \in \operatorname{\mathrm{ind}}(\Lambda )$
be projective-injective. Then,
![]() $X=P_x=I_z$
, for a pair of vertices x and z in
$X=P_x=I_z$
, for a pair of vertices x and z in
![]() $Q_0$
. Hence,
$Q_0$
. Hence,
![]() $X= \Lambda e_x$
and
$X= \Lambda e_x$
and
![]() $\operatorname{\mathrm{soc}}(X)$
is a subspace of
$\operatorname{\mathrm{soc}}(X)$
is a subspace of
![]() $e_z \Lambda e_x$
. Note that
$e_z \Lambda e_x$
. Note that
![]() $\operatorname{\mathrm{soc}}(X)$
is simple and
$\operatorname{\mathrm{soc}}(X)$
is simple and
![]() $\Lambda $
is basic. Then, we have
$\Lambda $
is basic. Then, we have
![]() $\dim _k(\operatorname{\mathrm{soc}}(X))=1$
. Consider the ideal
$\dim _k(\operatorname{\mathrm{soc}}(X))=1$
. Consider the ideal
![]() $J:=\langle \rho \rangle $
, where
$J:=\langle \rho \rangle $
, where
![]() $\rho $
denotes the element of
$\rho $
denotes the element of
![]() $e_z \Lambda e_x \subseteq kQ/I$
associated with
$e_z \Lambda e_x \subseteq kQ/I$
associated with
![]() $\operatorname{\mathrm{soc}}(X)$
. Then J is one-dimensional and
$\operatorname{\mathrm{soc}}(X)$
. Then J is one-dimensional and
![]() $JY=0$
if and only if
$JY=0$
if and only if
![]() $Y\not \simeq X$
. Consequently,
$Y\not \simeq X$
. Consequently,
![]() $\operatorname{\mathrm{brick}}(\Lambda ) \setminus \{X\} \subseteq \operatorname{\mathrm{brick}} (\Lambda /J) \subseteq \operatorname{\mathrm{brick}}(\Lambda )$
. Then, the first part of the assertion follows from Theorem 2.1. Moreover, the second part is an immediate consequence of the minimality assumption.
$\operatorname{\mathrm{brick}}(\Lambda ) \setminus \{X\} \subseteq \operatorname{\mathrm{brick}} (\Lambda /J) \subseteq \operatorname{\mathrm{brick}}(\Lambda )$
. Then, the first part of the assertion follows from Theorem 2.1. Moreover, the second part is an immediate consequence of the minimality assumption.
For
![]() $\Lambda =kQ/I$
, suppose a and z are, respectively, a source and a sink in
$\Lambda =kQ/I$
, suppose a and z are, respectively, a source and a sink in
![]() $(Q,I)$
. Let
$(Q,I)$
. Let
![]() $(Q',I')$
be the bound quiver obtained from
$(Q',I')$
be the bound quiver obtained from
![]() $(Q,I)$
by gluing the vertices a and z in Q, as follows: first, identify a and z, then kill all the composition of arrows
$(Q,I)$
by gluing the vertices a and z in Q, as follows: first, identify a and z, then kill all the composition of arrows
![]() $\beta \alpha $
, for each
$\beta \alpha $
, for each
![]() $\alpha $
incoming to z with any
$\alpha $
incoming to z with any
![]() $\beta $
outgoing from a. If v denotes a vertex of
$\beta $
outgoing from a. If v denotes a vertex of
![]() $(Q',I')$
obtained from gluing a sink and a source in
$(Q',I')$
obtained from gluing a sink and a source in
![]() $(Q,I)$
, then obviously v is a node. The reverse process of gluing is called resolving a node. It is well known that if
$(Q,I)$
, then obviously v is a node. The reverse process of gluing is called resolving a node. It is well known that if
![]() $\Lambda '$
is obtained from
$\Lambda '$
is obtained from
![]() $\Lambda $
via a sequence of gluing (resolving), then
$\Lambda $
via a sequence of gluing (resolving), then
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
are of the same representation type. In particular,
$\Lambda '$
are of the same representation type. In particular,
![]() $\Lambda $
is min-rep-inf algebra if and only if
$\Lambda $
is min-rep-inf algebra if and only if
![]() $\Lambda '$
is so.
$\Lambda '$
is so.
The following proposition shows that there is a fundamental difference between the bound quivers of min-
![]() $\tau $
-infinite algebras and min-rep-inf algebras. This result is already shown in [Reference MousavandM2, Th. 1.1], and thus we omit the proof.
$\tau $
-infinite algebras and min-rep-inf algebras. This result is already shown in [Reference MousavandM2, Th. 1.1], and thus we omit the proof.
Proposition 3.2 [Reference MousavandM2]
Let
![]() $\Lambda =kQ/I$
be a min-
$\Lambda =kQ/I$
be a min-
![]() $\tau $
-infinite algebra. Then,
$\tau $
-infinite algebra. Then,
![]() $(Q,I)$
does not contain any node.
$(Q,I)$
does not contain any node.
By the above proposition and the remark preceding that, one observes that for the classification of min-rep-inf algebras and min-
![]() $\tau $
-infinite algebras, we only need to treat the node-free bound quivers. Moreover, the proposition gives a simple sufficient condition for
$\tau $
-infinite algebras, we only need to treat the node-free bound quivers. Moreover, the proposition gives a simple sufficient condition for
![]() $\tau $
-tilting finiteness of a large family of min-rep-inf algebras. We note that, however, there also exist node-free min-rep-inf algebras which are
$\tau $
-tilting finiteness of a large family of min-rep-inf algebras. We note that, however, there also exist node-free min-rep-inf algebras which are
![]() $\tau $
-tilting finite (for explicit examples, see the wind wheel algebras in [Reference MousavandM1]).
$\tau $
-tilting finite (for explicit examples, see the wind wheel algebras in [Reference MousavandM1]).
As an important consequence of the previous proposition, we get an explicit criterion for
![]() $\tau $
-tilting (in)finiteness of algebras with radical square zero. We note that a classification of
$\tau $
-tilting (in)finiteness of algebras with radical square zero. We note that a classification of
![]() $\tau $
-tilting finite algebras with radical square zero also appears in [Reference AdachiAd], where Adachi uses the notion of separated quivers. However, as shown in Propositions 3.1 and 3.2, the reduction to the min-
$\tau $
-tilting finite algebras with radical square zero also appears in [Reference AdachiAd], where Adachi uses the notion of separated quivers. However, as shown in Propositions 3.1 and 3.2, the reduction to the min-
![]() $\tau $
-infinite algebras allows us to use the property of their bound quivers and obtain the same result via a less technical approach.
$\tau $
-infinite algebras allows us to use the property of their bound quivers and obtain the same result via a less technical approach.
To state the next result more succinctly, we say Q is a sink-source quiver if each vertex of Q is either a sink or a source.
Corollary 3.3 [Reference AdachiAd]
Provided that
![]() $\operatorname{\mathrm{rad}}^2(\Lambda )=0$
, the following are equivalent:
$\operatorname{\mathrm{rad}}^2(\Lambda )=0$
, the following are equivalent:
-
1.
 $\Lambda $
is
$\Lambda $
is
 $\tau $
-tilting infinite.
$\tau $
-tilting infinite. -
2. There exists an ideal J in
 $\Lambda $
such that
$\Lambda $
such that
 $\Lambda /J$
is hereditary of affine type with a sink-source quiver.
$\Lambda /J$
is hereditary of affine type with a sink-source quiver.
Proof. Suppose
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting infinite. Without loss of generality, we can assume
$\tau $
-tilting infinite. Without loss of generality, we can assume
![]() $\Lambda $
is min-
$\Lambda $
is min-
![]() $\tau $
-infinite. By Proposition 3.2,
$\tau $
-infinite. By Proposition 3.2,
![]() $\Lambda $
is node-free. Therefore,
$\Lambda $
is node-free. Therefore,
![]() $\operatorname{\mathrm{rad}}^2(\Lambda )=0$
implies that
$\operatorname{\mathrm{rad}}^2(\Lambda )=0$
implies that
![]() $\Lambda =kQ$
, for a sink-source quiver Q. To finish the proof, we use the fact that hereditary algebras of affine type are
$\Lambda =kQ$
, for a sink-source quiver Q. To finish the proof, we use the fact that hereditary algebras of affine type are
![]() $\tau $
-tilting infinite and obviously minimal with respect to this property.
$\tau $
-tilting infinite and obviously minimal with respect to this property.
For an affine quiver Q, it is well known that the path algebra
![]() $kQ$
admits a one-parameter family of bricks of the same length (e.g., [Reference Simson and SkowrońskiSS, Chap. 13]). Therefore, the following result is an immediate consequence of the above classification and verifies Conjecture 1.1 for the family of algebras with
$kQ$
admits a one-parameter family of bricks of the same length (e.g., [Reference Simson and SkowrońskiSS, Chap. 13]). Therefore, the following result is an immediate consequence of the above classification and verifies Conjecture 1.1 for the family of algebras with
![]() $\operatorname{\mathrm{rad}}^2(\Lambda )=0$
.
$\operatorname{\mathrm{rad}}^2(\Lambda )=0$
.
Corollary 3.4. A radical square zero algebra is
![]() $\tau $
-tilting infinite if and only if it admits a one-parameter family of bricks of the same length.
$\tau $
-tilting infinite if and only if it admits a one-parameter family of bricks of the same length.
Before showing another property of min-
![]() $\tau $
-infinite algebras, we remark that the center of a min-rep-inf algebra can be as large as the entire algebra. For instance,
$\tau $
-infinite algebras, we remark that the center of a min-rep-inf algebra can be as large as the entire algebra. For instance,
![]() $k\langle x,y\rangle /\langle x^2, y^2, xy, yx \rangle $
is a commutative string algebra which is min-rep-inf. This algebra is in fact obtained by gluing the source and sink in the Kronecker quiver. In contrast, our following result shows that the behavior of min-
$k\langle x,y\rangle /\langle x^2, y^2, xy, yx \rangle $
is a commutative string algebra which is min-rep-inf. This algebra is in fact obtained by gluing the source and sink in the Kronecker quiver. In contrast, our following result shows that the behavior of min-
![]() $\tau $
-infinite algebras with respect to their center is very different from their classical counterparts.
$\tau $
-infinite algebras with respect to their center is very different from their classical counterparts.
Proposition 3.5. Every min-
![]() $\tau $
-infinite algebra is central.
$\tau $
-infinite algebra is central.
Proof. As a consequence of [Reference Eisele, Janssens and RaedscheldersEJR, Th. 1] and [Reference Demonet, Iyama and JassoDIJ], for any algebra
![]() $\Lambda $
and each ideal J generated by some elements in
$\Lambda $
and each ideal J generated by some elements in
![]() $Z(\Lambda )\cap \operatorname{\mathrm{rad}}(\Lambda )$
, the sets
$Z(\Lambda )\cap \operatorname{\mathrm{rad}}(\Lambda )$
, the sets
![]() $\tau \operatorname{\mathrm{rigid}}(\Lambda )\cap \operatorname{\mathrm{ind}}(\Lambda )$
and
$\tau \operatorname{\mathrm{rigid}}(\Lambda )\cap \operatorname{\mathrm{ind}}(\Lambda )$
and
![]() $\tau \operatorname{\mathrm{rigid}} (\Lambda /J)\cap \operatorname{\mathrm{ind}}(\Lambda /I)$
are in bijection. In particular,
$\tau \operatorname{\mathrm{rigid}} (\Lambda /J)\cap \operatorname{\mathrm{ind}}(\Lambda /I)$
are in bijection. In particular,
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite if and only if
$\tau $
-tilting finite if and only if
![]() $\Lambda /J$
is so.
$\Lambda /J$
is so.
Now, assume
![]() $\Lambda =kQ/I$
is min-
$\Lambda =kQ/I$
is min-
![]() $\tau $
-infinite. Obviously,
$\tau $
-infinite. Obviously,
![]() $|Q_0|=n \geq 2$
(otherwise,
$|Q_0|=n \geq 2$
(otherwise,
![]() $\Lambda $
is local and therefore
$\Lambda $
is local and therefore
![]() $\tau $
-tilting finite). Moreover, by the minimality assumption, we have
$\tau $
-tilting finite). Moreover, by the minimality assumption, we have
![]() $Z(\Lambda ) \cap \operatorname{\mathrm{rad}}(\Lambda )=0$
.
$Z(\Lambda ) \cap \operatorname{\mathrm{rad}}(\Lambda )=0$
.
Every element of
![]() $\Lambda =kQ/I$
can be expressed as
$\Lambda =kQ/I$
can be expressed as
![]() $\rho :=\sum _{i=1}^{n} \lambda _i e_i+ r+I$
, where
$\rho :=\sum _{i=1}^{n} \lambda _i e_i+ r+I$
, where
![]() $\lambda _i \in k$
, and r is a linear combination of paths of positive length in Q. Suppose
$\lambda _i \in k$
, and r is a linear combination of paths of positive length in Q. Suppose
![]() $\alpha $
is an arrow in Q with
$\alpha $
is an arrow in Q with
![]() $s(\alpha )=i$
and
$s(\alpha )=i$
and
![]() $e(\alpha )=j$
. Then, multiplying
$e(\alpha )=j$
. Then, multiplying
![]() $\rho $
by
$\rho $
by
![]() $\alpha $
from the left and from the right, and then reducing modulo
$\alpha $
from the left and from the right, and then reducing modulo
![]() $\operatorname{\mathrm{rad}}^2 (\Lambda )$
, we get
$\operatorname{\mathrm{rad}}^2 (\Lambda )$
, we get
![]() $\lambda _i \alpha =\lambda _j \alpha $
. Since Q is a connected quiver, we have all
$\lambda _i \alpha =\lambda _j \alpha $
. Since Q is a connected quiver, we have all
![]() $\lambda _i$
are equal. Consequently, we have
$\lambda _i$
are equal. Consequently, we have
![]() $\rho = \lambda \cdot 1 + r + I$
, for some
$\rho = \lambda \cdot 1 + r + I$
, for some
![]() $\lambda \in k$
. Since
$\lambda \in k$
. Since
![]() $\lambda \cdot 1 + I \in Z(\Lambda )$
, we get that
$\lambda \cdot 1 + I \in Z(\Lambda )$
, we get that
![]() $r + I \in Z(\Lambda )$
. Moreover, from
$r + I \in Z(\Lambda )$
. Moreover, from
![]() $Z(A) \cap \operatorname{\mathrm{rad}}(\Lambda )= 0$
, it follows that
$Z(A) \cap \operatorname{\mathrm{rad}}(\Lambda )= 0$
, it follows that
![]() $r \in I$
. Therefore,
$r \in I$
. Therefore,
![]() $\rho = \lambda \cdot 1$
.
$\rho = \lambda \cdot 1$
.
As discussed in §2.3, for an algebra
![]() $\Lambda $
, both for the min-rep-inf and the min-
$\Lambda $
, both for the min-rep-inf and the min-
![]() $\tau $
-infinite algebras, the minimality conditions are defined with respect to certain sets of isomorphism classes of modules of finite length over
$\tau $
-infinite algebras, the minimality conditions are defined with respect to certain sets of isomorphism classes of modules of finite length over
![]() $\Lambda $
and the corresponding sets on the quotient algebras
$\Lambda $
and the corresponding sets on the quotient algebras
![]() $\Lambda /J$
. In our next proposition, we give analogous characterizations of these minimality conditions in terms of certain modules of infinite lengths. To do so, we recall an elegant characterization of rep-inf algebras by Auslander [Reference Aihara and IyamaAu]. Recently, Sentieri [Reference SentieriSe] has shown a brick version of this theorem of Auslander. The following theorem collects both of the results.
$\Lambda /J$
. In our next proposition, we give analogous characterizations of these minimality conditions in terms of certain modules of infinite lengths. To do so, we recall an elegant characterization of rep-inf algebras by Auslander [Reference Aihara and IyamaAu]. Recently, Sentieri [Reference SentieriSe] has shown a brick version of this theorem of Auslander. The following theorem collects both of the results.
Theorem 3.6 [Reference Aihara and IyamaAu] and [Reference SentieriSe]
Let
![]() $\Lambda $
be an algebra. Then:
$\Lambda $
be an algebra. Then:
-
1.
 $\Lambda $
is representation-finite if and only if any
$\Lambda $
is representation-finite if and only if any
 $M \in \operatorname{\mathrm{Ind}}(\Lambda )$
is finitely generated.
$M \in \operatorname{\mathrm{Ind}}(\Lambda )$
is finitely generated. -
2.
 $\Lambda $
is brick-finite if and only if any
$\Lambda $
is brick-finite if and only if any
 $M \in \operatorname{\mathrm{Brick}}(\Lambda )$
is finitely generated.
$M \in \operatorname{\mathrm{Brick}}(\Lambda )$
is finitely generated.
Building upon the preceding theorem, we obtain new characterizations of the minimality conditions treated in this paper. We recall that a module over
![]() $\Lambda $
is faithful if its annihilator is trivial.
$\Lambda $
is faithful if its annihilator is trivial.
Proposition 3.7. Let
![]() $\Lambda $
be an algebra. Then:
$\Lambda $
be an algebra. Then:
-
1. If
 $\Lambda $
is rep-inf, then it is min-rep-inf if and only if every
$\Lambda $
is rep-inf, then it is min-rep-inf if and only if every
 $M \in \operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
is faithful.
$M \in \operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
is faithful. -
2. If
 $\Lambda $
is
$\Lambda $
is
 $\tau $
-tilting infinite, then it is min-
$\tau $
-tilting infinite, then it is min-
 $\tau $
-infinite if and only if every
$\tau $
-infinite if and only if every
 $N \in \operatorname{\mathrm{Brick}}(\Lambda )\setminus \operatorname{\mathrm{brick}}(\Lambda )$
is faithful.
$N \in \operatorname{\mathrm{Brick}}(\Lambda )\setminus \operatorname{\mathrm{brick}}(\Lambda )$
is faithful.
Proof. To show
![]() $(1)$
, suppose
$(1)$
, suppose
![]() $\Lambda $
is min-rep-inf. If there exists
$\Lambda $
is min-rep-inf. If there exists
![]() $M \in \operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
with
$M \in \operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
with
![]() $\operatorname{\mathrm{ann}}_{\Lambda }(M)\neq 0$
, then for the quotient algebra
$\operatorname{\mathrm{ann}}_{\Lambda }(M)\neq 0$
, then for the quotient algebra
![]() $\Lambda ':=\Lambda /\langle \operatorname{\mathrm{ann}}_{\Lambda }(M) \rangle $
, we have
$\Lambda ':=\Lambda /\langle \operatorname{\mathrm{ann}}_{\Lambda }(M) \rangle $
, we have
![]() $M \in \operatorname{\mathrm{Ind}}(\Lambda ')\setminus \operatorname{\mathrm{ind}}(\Lambda ')$
. Since
$M \in \operatorname{\mathrm{Ind}}(\Lambda ')\setminus \operatorname{\mathrm{ind}}(\Lambda ')$
. Since
![]() $\Lambda '$
is rep-finite, the desired contradiction follows from Theorem 3.6.
$\Lambda '$
is rep-finite, the desired contradiction follows from Theorem 3.6.
For the converse, let us assume that
![]() $\Lambda $
is not min-rep-infinite. Thus, for some nonzero ideal
$\Lambda $
is not min-rep-infinite. Thus, for some nonzero ideal
![]() $J \in \Lambda $
, the quotient algebra
$J \in \Lambda $
, the quotient algebra
![]() $\Lambda /J$
is rep-infinite and, again by Theorem 3.6, there exists M in
$\Lambda /J$
is rep-infinite and, again by Theorem 3.6, there exists M in
![]() $\operatorname{\mathrm{Ind}}(\Lambda /J)\setminus \operatorname{\mathrm{ind}}(\Lambda /J)$
. However, M also belongs to
$\operatorname{\mathrm{Ind}}(\Lambda /J)\setminus \operatorname{\mathrm{ind}}(\Lambda /J)$
. However, M also belongs to
![]() $\operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
and it is not faithful. So, we get the desired contradiction.
$\operatorname{\mathrm{Ind}}(\Lambda )\setminus \operatorname{\mathrm{ind}}(\Lambda )$
and it is not faithful. So, we get the desired contradiction.
In the above proof, if we replace the indecomposable modules by bricks, we obtain a proof of
![]() $(2)$
.
$(2)$
.
4 Minimal tilting infinite algebras
Now, we change our perspective and study the min-
![]() $\tau $
-infinite algebras in the setting of classical tilting theory. Our main theorem in this section results in a good understanding of tilting modules and their mutation graph for min-
$\tau $
-infinite algebras in the setting of classical tilting theory. Our main theorem in this section results in a good understanding of tilting modules and their mutation graph for min-
![]() $\tau $
-infinite algebras. Before we show the main result of the section, we need some basic facts.
$\tau $
-infinite algebras. Before we show the main result of the section, we need some basic facts.
Proposition 4.1. [Reference AuslanderASS, VIII.5.1] A
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $\Lambda $
-module is partial tilting provided that it is faithful. In particular,
$\Lambda $
-module is partial tilting provided that it is faithful. In particular,
![]() $\operatorname{\mathrm{tilt}}(\Lambda )$
consists of faithful modules in
$\operatorname{\mathrm{tilt}}(\Lambda )$
consists of faithful modules in
![]() $\tau \operatorname{-\textrm{tilt}}(\Lambda )$
.
$\tau \operatorname{-\textrm{tilt}}(\Lambda )$
.
For a basic
![]() $\Lambda $
-module M, recall that
$\Lambda $
-module M, recall that
![]() $\operatorname {Fac}(M)$
denotes the subcategory of
$\operatorname {Fac}(M)$
denotes the subcategory of
![]() $\operatorname{\mathrm{mod}} \Lambda $
which consists of all quotients of direct sums of M. In particular, if M is
$\operatorname{\mathrm{mod}} \Lambda $
which consists of all quotients of direct sums of M. In particular, if M is
![]() $\tau $
-rigid, then
$\tau $
-rigid, then
![]() $\operatorname {Fac}(M)$
is a functorially finite torsion class in
$\operatorname {Fac}(M)$
is a functorially finite torsion class in
![]() $\operatorname{\mathrm{mod}} \Lambda $
. If M belongs to
$\operatorname{\mathrm{mod}} \Lambda $
. If M belongs to
![]() $\operatorname {\tau -rigid} (\Lambda ) \setminus s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, then it is a summand of a basic support
$\operatorname {\tau -rigid} (\Lambda ) \setminus s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, then it is a summand of a basic support
![]() $\tau $
-tilting module T, which is given by the direct sum of all indecomposable
$\tau $
-tilting module T, which is given by the direct sum of all indecomposable
![]() $\operatorname {Ext}$
-projective modules in
$\operatorname {Ext}$
-projective modules in
![]() $\operatorname {Fac}(M)$
(for details, see [Reference Assem, Simson and SkowrońskiAIR]).
$\operatorname {Fac}(M)$
(for details, see [Reference Assem, Simson and SkowrońskiAIR]).
Now, we are ready to prove the following theorem, which establishes interesting connections between our results on min-
![]() $\tau $
-infinite algebras and tilting theory.
$\tau $
-infinite algebras and tilting theory.
Theorem 4.2. Let
![]() $\Lambda $
be min-
$\Lambda $
be min-
![]() $\tau $
-infinite. Then, almost all
$\tau $
-infinite. Then, almost all
![]() $\tau $
-rigid modules are faithful, thus partial tilting.
$\tau $
-rigid modules are faithful, thus partial tilting.
Proof. Suppose
![]() $\{T_i\}_{i\in \mathbb {N}}$
is a family of pairwise non-isomorphic unfaithful modules in
$\{T_i\}_{i\in \mathbb {N}}$
is a family of pairwise non-isomorphic unfaithful modules in
![]() $\operatorname {\tau -rigid}(\Lambda )$
, and let
$\operatorname {\tau -rigid}(\Lambda )$
, and let
![]() $\mathcal {T}_i = \mathrm {Fac}(T_i)$
be the corresponding functorially finite torsion classes. From the beginning, we can assume every
$\mathcal {T}_i = \mathrm {Fac}(T_i)$
be the corresponding functorially finite torsion classes. From the beginning, we can assume every
![]() $T_i$
is a nonzero support
$T_i$
is a nonzero support
![]() $\tau $
-tilting module.
$\tau $
-tilting module.
We want to construct an infinite strictly ascending chain of functorially finite torsion classes as follows. Set
![]() $\mathcal {U}_0 : = \{0\}$
, which is clearly functorially finite and is contained in all
$\mathcal {U}_0 : = \{0\}$
, which is clearly functorially finite and is contained in all
![]() $\mathcal {T}_i$
. It follows from [Reference Demonet, Iyama and JassoDIJ, Th. 1.3] that for each j, there is a right mutation
$\mathcal {T}_i$
. It follows from [Reference Demonet, Iyama and JassoDIJ, Th. 1.3] that for each j, there is a right mutation
![]() $\mathcal {U}_{1}^j$
of
$\mathcal {U}_{1}^j$
of
![]() $\mathcal {U}_0$
with
$\mathcal {U}_0$
with
![]() $\mathcal {U}_0 \subsetneq \mathcal {U}_{1}^j \subseteq \mathcal {T}_j$
. Since the Hasse quiver of the poset of functorially finite torsion classes of
$\mathcal {U}_0 \subsetneq \mathcal {U}_{1}^j \subseteq \mathcal {T}_j$
. Since the Hasse quiver of the poset of functorially finite torsion classes of
![]() $\mathrm {mod}\Lambda $
is n-regular, there is a (functorially finite) right mutation
$\mathrm {mod}\Lambda $
is n-regular, there is a (functorially finite) right mutation
![]() $\mathcal {U}_1$
of
$\mathcal {U}_1$
of
![]() $\mathcal {U}_0$
such that
$\mathcal {U}_0$
such that
![]() $\mathcal {U}_1^j = \mathcal {U}_1$
for infinitely many
$\mathcal {U}_1^j = \mathcal {U}_1$
for infinitely many
![]() $j \in \mathbb {N}$
. Note that for all but at most one such j, the inclusion
$j \in \mathbb {N}$
. Note that for all but at most one such j, the inclusion
![]() $\mathcal {U}_1 \subseteq \mathcal {T}_j$
is proper. By induction, assume that we have constructed a functorially finite torsion class
$\mathcal {U}_1 \subseteq \mathcal {T}_j$
is proper. By induction, assume that we have constructed a functorially finite torsion class
![]() $\mathcal {U}_i$
that is properly contained in infinitely many
$\mathcal {U}_i$
that is properly contained in infinitely many
![]() $\mathcal {T}_j$
. For any such j, we again apply [Reference Demonet, Iyama and JassoDIJ, Th. 1.3] to get a right mutation
$\mathcal {T}_j$
. For any such j, we again apply [Reference Demonet, Iyama and JassoDIJ, Th. 1.3] to get a right mutation
![]() $\mathcal {U}_{i+1}^j$
of
$\mathcal {U}_{i+1}^j$
of
![]() $\mathcal {U}_i$
with
$\mathcal {U}_i$
with
![]() $\mathcal {U}_i \subsetneq \mathcal {U}_{i+1}^j \subseteq \mathcal {T}_j$
. As before, we construct
$\mathcal {U}_i \subsetneq \mathcal {U}_{i+1}^j \subseteq \mathcal {T}_j$
. As before, we construct
![]() $\mathcal {U}_{i+1}$
as a functorially finite torsion class that coincides with infinitely many of the
$\mathcal {U}_{i+1}$
as a functorially finite torsion class that coincides with infinitely many of the
![]() $\mathcal {U}_{i+1}^j$
. Once again, observe that
$\mathcal {U}_{i+1}^j$
. Once again, observe that
![]() $\mathcal {U}_{i+1}^j \subseteq \mathcal {T}_j$
is proper for infinitely many j. This yields a chain
$\mathcal {U}_{i+1}^j \subseteq \mathcal {T}_j$
is proper for infinitely many j. This yields a chain
of functorially finite torsion classes such that each
![]() $\mathcal {U}_i$
is contained in infinitely many
$\mathcal {U}_i$
is contained in infinitely many
![]() $\mathcal {T}_j$
. Because each
$\mathcal {T}_j$
. Because each
![]() $\mathcal {T}_j$
is unfaithful, so is every
$\mathcal {T}_j$
is unfaithful, so is every
![]() $\mathcal {U}_i$
. If
$\mathcal {U}_i$
. If
![]() $J_i$
denotes the annihilator of
$J_i$
denotes the annihilator of
![]() $\mathcal {U}_i$
, we get a corresponding descending chain
$\mathcal {U}_i$
, we get a corresponding descending chain
of nonzero ideals. Since ideals of
![]() $\Lambda $
are finite-dimensional, this chain has to stabilize to a nonzero ideal I, implying that there is a positive integer r such that
$\Lambda $
are finite-dimensional, this chain has to stabilize to a nonzero ideal I, implying that there is a positive integer r such that
![]() $I = J_{r+j}$
for all
$I = J_{r+j}$
for all
![]() $j \ge 0$
. For all
$j \ge 0$
. For all
![]() $i \in \mathbb {N}$
, observe that each
$i \in \mathbb {N}$
, observe that each
![]() $\mathcal {U}_i$
, and therefore the algebra
$\mathcal {U}_i$
, and therefore the algebra
![]() $\Lambda /J_i$
, has at least i non-isomorphic bricks. Indeed, for each i, there is at least one brick that belongs to
$\Lambda /J_i$
, has at least i non-isomorphic bricks. Indeed, for each i, there is at least one brick that belongs to
![]() $\mathcal {U}_i$
but not to
$\mathcal {U}_i$
but not to
![]() $\mathcal {U}_{i-1}$
. Thus,
$\mathcal {U}_{i-1}$
. Thus,
![]() $\Lambda /I$
has infinitely many non-isomorphic bricks, and by Theorem 2.1,
$\Lambda /I$
has infinitely many non-isomorphic bricks, and by Theorem 2.1,
![]() $\Lambda /I$
is
$\Lambda /I$
is
![]() $\tau $
-tilting infinite. This contradicts the minimality assumption on
$\tau $
-tilting infinite. This contradicts the minimality assumption on
![]() $\Lambda $
. Thus, almost every
$\Lambda $
. Thus, almost every
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $\Lambda $
-module is faithful.
$\Lambda $
-module is faithful.
The last assertion follows from the fact that, for any algebra, any faithful
![]() $\tau $
-rigid module is partial tilting.
$\tau $
-rigid module is partial tilting.
Remark 4.3. For any min-
![]() $\tau $
-infinite algebra
$\tau $
-infinite algebra
![]() $\Lambda $
, Theorem 4.2 implies that for almost all
$\Lambda $
, Theorem 4.2 implies that for almost all
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $\Lambda $
-modules, we have
$\Lambda $
-modules, we have
![]() $\operatorname{\mathrm{pd}}_{\Lambda }(X)=1$
, and therefore
$\operatorname{\mathrm{pd}}_{\Lambda }(X)=1$
, and therefore
![]() $\tau _{\Lambda }(X)=\mathrm {D}\operatorname {Ext}^1_{\Lambda }(X,\Lambda )$
. This is interesting, particularly because there exist min-
$\tau _{\Lambda }(X)=\mathrm {D}\operatorname {Ext}^1_{\Lambda }(X,\Lambda )$
. This is interesting, particularly because there exist min-
![]() $\tau $
-infinite algebras of infinite global dimension. The generalized barbell algebras studied in [Reference MousavandM2] are shown to be min-
$\tau $
-infinite algebras of infinite global dimension. The generalized barbell algebras studied in [Reference MousavandM2] are shown to be min-
![]() $\tau $
-infinite, but one can easily observe that they could be of infinite global dimension.
$\tau $
-infinite, but one can easily observe that they could be of infinite global dimension.
In the previous theorem, we note that the corresponding statement for bricks is not true. Namely, a min-
![]() $\tau $
-infinite algebra may admit infinitely many isomorphism classes of unfaithful bricks. For instance, all regular bricks over the Kronecker algebra are unfaithful. We further remark that there exist
$\tau $
-infinite algebra may admit infinitely many isomorphism classes of unfaithful bricks. For instance, all regular bricks over the Kronecker algebra are unfaithful. We further remark that there exist
![]() $\tau $
-tilting infinite algebras
$\tau $
-tilting infinite algebras
![]() $\Lambda $
such that almost all
$\Lambda $
such that almost all
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $\Lambda $
-module are faithful, but
$\Lambda $
-module are faithful, but
![]() $\Lambda $
is not min-
$\Lambda $
is not min-
![]() $\tau $
-infinite. For example, every indecomposable rigid module of the
$\tau $
-infinite. For example, every indecomposable rigid module of the
![]() $3$
-Kronecker quiver is preprojective or preinjective. In this case, almost all
$3$
-Kronecker quiver is preprojective or preinjective. In this case, almost all
![]() $\tau $
-rigid modules are faithful.
$\tau $
-rigid modules are faithful.
Before we state an important consequence of Theorem 4.2, note that for an arbitrary algebra
![]() $\Lambda $
, we may have
$\Lambda $
, we may have
![]() $|\tau \operatorname{-\textrm{tilt}}(\Lambda ) \setminus \operatorname{\mathrm{tilt}}(\Lambda )|= \infty $
. In particular, a
$|\tau \operatorname{-\textrm{tilt}}(\Lambda ) \setminus \operatorname{\mathrm{tilt}}(\Lambda )|= \infty $
. In particular, a
![]() $\tau $
-tilting infinite algebra
$\tau $
-tilting infinite algebra
![]() $\Lambda $
can admit only one tilting module. For instance, take the double Kronecker quiver (with two arrows
$\Lambda $
can admit only one tilting module. For instance, take the double Kronecker quiver (with two arrows
![]() $a, b: 1 \to 2$
and two arrows
$a, b: 1 \to 2$
and two arrows
![]() $a', b': 2 \to 1$
) modulo the ideal generated by
$a', b': 2 \to 1$
) modulo the ideal generated by
![]() $\langle aa' + bb', a'a+b'b, ab', ba', a'b, b'a \rangle $
. The corresponding algebra is self-injective. However, it contains the Kronecker quiver as a subquiver, and therefore it is
$\langle aa' + bb', a'a+b'b, ab', ba', a'b, b'a \rangle $
. The corresponding algebra is self-injective. However, it contains the Kronecker quiver as a subquiver, and therefore it is
![]() $\tau $
-tilting infinite.
$\tau $
-tilting infinite.
Roughly speaking, our next result shows that for a min-
![]() $\tau $
-infinite algebra
$\tau $
-infinite algebra
![]() $\Lambda $
, the two sets
$\Lambda $
, the two sets
![]() $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
and
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
and
![]() $\operatorname{\mathrm{tilt}}(\Lambda )$
are almost the same. This is far from obvious and suggests that min-
$\operatorname{\mathrm{tilt}}(\Lambda )$
are almost the same. This is far from obvious and suggests that min-
![]() $\tau $
-infinite algebras can be useful in the study of some classical problems in tilting theory. In particular, it implies that over any min-
$\tau $
-infinite algebras can be useful in the study of some classical problems in tilting theory. In particular, it implies that over any min-
![]() $\tau $
-infinite algebra
$\tau $
-infinite algebra
![]() $\Lambda $
, the mutation graph of
$\Lambda $
, the mutation graph of
![]() $\operatorname{\mathrm{tilt}}(\Lambda )$
is infinite and n-regular at almost all vertices.
$\operatorname{\mathrm{tilt}}(\Lambda )$
is infinite and n-regular at almost all vertices.
To state our result more precisely, we say
![]() $\Lambda $
is minimal tilting infinite if it admits infinitely many tilting modules, up to isomorphism, but each proper quotient algebra
$\Lambda $
is minimal tilting infinite if it admits infinitely many tilting modules, up to isomorphism, but each proper quotient algebra
![]() $\Lambda /J$
has only finitely many tilting modules.
$\Lambda /J$
has only finitely many tilting modules.
Corollary 4.4. If
![]() $\Lambda $
is a min-
$\Lambda $
is a min-
![]() $\tau $
-infinite algebra, then almost all support
$\tau $
-infinite algebra, then almost all support
![]() $\tau $
-tilting modules are tilting. Therefore, an algebra is minimal tilting infinite if and only if it is min-
$\tau $
-tilting modules are tilting. Therefore, an algebra is minimal tilting infinite if and only if it is min-
![]() $\tau $
-infinite.
$\tau $
-infinite.
Proof. This follows from the inclusions
![]() $\operatorname{\mathrm{tilt}}(\Lambda ) \subseteq \tau \operatorname{-\textrm{tilt}}(\Lambda ) \subseteq s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, and the fact that
$\operatorname{\mathrm{tilt}}(\Lambda ) \subseteq \tau \operatorname{-\textrm{tilt}}(\Lambda ) \subseteq s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, and the fact that
![]() $\tau \operatorname{-\textrm{tilt}}(\Lambda )$
consists of sincere modules in
$\tau \operatorname{-\textrm{tilt}}(\Lambda )$
consists of sincere modules in
![]() $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
. By Theorem 4.2, almost all support
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
. By Theorem 4.2, almost all support
![]() $\tau $
-tilting
$\tau $
-tilting
![]() $\Lambda $
-modules are faithful as
$\Lambda $
-modules are faithful as
![]() $\Lambda $
-modules, and thus almost all
$\Lambda $
-modules, and thus almost all
![]() $\tau $
-tilting modules are tilting. It is evident that if
$\tau $
-tilting modules are tilting. It is evident that if
![]() $\Lambda $
is a min-
$\Lambda $
is a min-
![]() $\tau $
-inf algebra, then it must be minimal tilting infinite. If the converse fails, there exists a proper quotient
$\tau $
-inf algebra, then it must be minimal tilting infinite. If the converse fails, there exists a proper quotient
![]() $\Lambda /J$
which is min-
$\Lambda /J$
which is min-
![]() $\tau $
-infinite. Now, the desired contradiction immediately follows from the first part.
$\tau $
-infinite. Now, the desired contradiction immediately follows from the first part.
Remark 4.5. For a given algebra
![]() $\Lambda $
, it is a priori a hard problem to describe the mutation graph of tilting modules, and even harder to decide whether all proper quotients of
$\Lambda $
, it is a priori a hard problem to describe the mutation graph of tilting modules, and even harder to decide whether all proper quotients of
![]() $\Lambda $
admit finite mutation graphs. This is partially because the notion of tilting finiteness is not preserved under taking quotients. The previous corollary is significant in the sense that it yields an elegant classification of those algebras which are tilting infinite, but all of their proper quotients are tilting-finite. Thanks to Theorem 2.1, this classification could be stated in terms of bricks rather than tilting modules, which could have its own advantages, especially if one is interested in the study of geometric representation theory. In that setting, bricks coincide with points having trivial stabilizers. Therefore, they are decisive in the study of moduli spaces of finite-dimensional algebras (see, e.g., [Reference KingK]).
$\Lambda $
admit finite mutation graphs. This is partially because the notion of tilting finiteness is not preserved under taking quotients. The previous corollary is significant in the sense that it yields an elegant classification of those algebras which are tilting infinite, but all of their proper quotients are tilting-finite. Thanks to Theorem 2.1, this classification could be stated in terms of bricks rather than tilting modules, which could have its own advantages, especially if one is interested in the study of geometric representation theory. In that setting, bricks coincide with points having trivial stabilizers. Therefore, they are decisive in the study of moduli spaces of finite-dimensional algebras (see, e.g., [Reference KingK]).
From the preceding corollary and Theorem 3.3, the following result is immediate.
Corollary 4.6. Let
![]() $\Lambda =kQ/I$
with
$\Lambda =kQ/I$
with
![]() $\operatorname{\mathrm{rad}}^2(\Lambda )=0$
. If
$\operatorname{\mathrm{rad}}^2(\Lambda )=0$
. If
![]() $\operatorname{\mathrm{tilt}}(\Lambda )$
is an infinite set, then Q contains a subquiver
$\operatorname{\mathrm{tilt}}(\Lambda )$
is an infinite set, then Q contains a subquiver
![]() $Q'$
which is sink-source affine type.
$Q'$
which is sink-source affine type.
Remark 4.7. It is well known that the study of
![]() $\tau $
-tilting theory closely relates to that of silting theory. In particular, for an algebra
$\tau $
-tilting theory closely relates to that of silting theory. In particular, for an algebra
![]() $\Lambda $
, in [Reference Aoki and YurikusaAMV], the authors show that finite-dimensional silting modules in
$\Lambda $
, in [Reference Aoki and YurikusaAMV], the authors show that finite-dimensional silting modules in
![]() $\operatorname{\mathrm{Mod}} \Lambda $
are exactly the support
$\operatorname{\mathrm{Mod}} \Lambda $
are exactly the support
![]() $\tau $
-tilting
$\tau $
-tilting
![]() $\Lambda $
-modules. Thus, an algebra
$\Lambda $
-modules. Thus, an algebra
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting-finite if and only if all torsion classes are generated by basic finite dimensional silting
$\tau $
-tilting-finite if and only if all torsion classes are generated by basic finite dimensional silting
![]() $\Lambda $
-modules. This is the case if and only if all silting modules in
$\Lambda $
-modules. This is the case if and only if all silting modules in
![]() $\operatorname{\mathrm{Mod}} \Lambda $
, up to some equivalence, are finite-dimensional. This allows us to establish a connection between minimality conditions among
$\operatorname{\mathrm{Mod}} \Lambda $
, up to some equivalence, are finite-dimensional. This allows us to establish a connection between minimality conditions among
![]() $\tau $
-tilting infinite and silting infinite algebras. In particular, if
$\tau $
-tilting infinite and silting infinite algebras. In particular, if
![]() $\Lambda $
is min-
$\Lambda $
is min-
![]() $\tau $
-infinite, there exists a (definable) torsion class in
$\tau $
-infinite, there exists a (definable) torsion class in
![]() $\operatorname{\mathrm{Tors}}(\Lambda )$
such that the associated silting module, up to equivalence, is not finite-dimensional. It is immediate that if
$\operatorname{\mathrm{Tors}}(\Lambda )$
such that the associated silting module, up to equivalence, is not finite-dimensional. It is immediate that if
![]() $\Lambda '$
is a proper quotient of
$\Lambda '$
is a proper quotient of
![]() $\Lambda $
, all silting
$\Lambda $
, all silting
![]() $\Lambda '$
-modules, up to equivalence, are finite-dimensional and hence
$\Lambda '$
-modules, up to equivalence, are finite-dimensional and hence
![]() $\Lambda '$
admits only finitely many basic silting modules. Therefore, as long as silting modules are considered up to equivalence, an algebra
$\Lambda '$
admits only finitely many basic silting modules. Therefore, as long as silting modules are considered up to equivalence, an algebra
![]() $\Lambda $
is min-
$\Lambda $
is min-
![]() $\tau $
-infinite if and only if it is minimal silting infinite.
$\tau $
-infinite if and only if it is minimal silting infinite.
5 Reduction of the conjecture
In the current section, we return to Conjecture 1.1 and verify it for some families of min-
![]() $\tau $
-infinite algebras. Consequently, we obtain Theorem 1.4, as a reduction of Conjecture 1.1 to a particular subfamily of min-
$\tau $
-infinite algebras. Consequently, we obtain Theorem 1.4, as a reduction of Conjecture 1.1 to a particular subfamily of min-
![]() $\tau $
-infinite algebras. Before we show the main result of this section, we need some preparation.
$\tau $
-infinite algebras. Before we show the main result of this section, we need some preparation.
Lemma 5.1. Let
![]() $\{I_i\}_{i \in \mathbb {N}}$
be an infinite subset of
$\{I_i\}_{i \in \mathbb {N}}$
be an infinite subset of
![]() $\operatorname{\mathrm{Ideal}}(\Lambda )$
such that the corresponding algebras
$\operatorname{\mathrm{Ideal}}(\Lambda )$
such that the corresponding algebras
![]() $\Lambda /I_i$
are all isomorphic. If
$\Lambda /I_i$
are all isomorphic. If
![]() $\Lambda /I_1$
has a faithful brick of dimension d, then
$\Lambda /I_1$
has a faithful brick of dimension d, then
![]() $\Lambda $
admits infinitely many non-isomorphic bricks of dimension d.
$\Lambda $
admits infinitely many non-isomorphic bricks of dimension d.
Proof. Let B be a faithful brick of dimension d in
![]() $\operatorname{\mathrm{mod}} \Lambda /I_1$
. For each
$\operatorname{\mathrm{mod}} \Lambda /I_1$
. For each
![]() $i \ge 2$
, let
$i \ge 2$
, let
![]() $B_i$
be the brick of
$B_i$
be the brick of
![]() $\Lambda /I_i$
induced from the isomorphism
$\Lambda /I_i$
induced from the isomorphism
![]() $\varphi _i: \Lambda /I_i \to \Lambda /I_1$
. Then
$\varphi _i: \Lambda /I_i \to \Lambda /I_1$
. Then
![]() $B_i$
is faithful of dimension d. The
$B_i$
is faithful of dimension d. The
![]() $B_i$
are non-isomorphic as
$B_i$
are non-isomorphic as
![]() $\Lambda $
-modules since they have pairwise distinct annihilators.
$\Lambda $
-modules since they have pairwise distinct annihilators.
Note that any algebra that satisfies the assumption of the previous lemma must be nondistributive. We postpone a more detailed study of
![]() $\tau $
-tilting (in)finiteness of nondistributive algebras to our future work.
$\tau $
-tilting (in)finiteness of nondistributive algebras to our future work.
Let
![]() $\Lambda $
be a min-
$\Lambda $
be a min-
![]() $\tau $
-infinite algebra such that it admits an infinite family
$\tau $
-infinite algebra such that it admits an infinite family
![]() $\{B_i\}_{i \in \mathbb {N}}$
of (non-isomorphic) unfaithful bricks, with
$\{B_i\}_{i \in \mathbb {N}}$
of (non-isomorphic) unfaithful bricks, with
![]() $I_i:=\operatorname{\mathrm{ann}}_{\Lambda }B_i$
, for
$I_i:=\operatorname{\mathrm{ann}}_{\Lambda }B_i$
, for
![]() $i \in \mathbb {N}$
. By the minimality assumption on
$i \in \mathbb {N}$
. By the minimality assumption on
![]() $\Lambda $
, these ideals must form an infinite family. Without loss of generality, assume that they are pairwise distinct and consider the algebras
$\Lambda $
, these ideals must form an infinite family. Without loss of generality, assume that they are pairwise distinct and consider the algebras
![]() $\Lambda /I_i$
for
$\Lambda /I_i$
for
![]() $i \ge 1$
. Looking at these algebras up to isomorphisms, we have either a finite family, or an infinite family. In the former case, we apply Lemma 5.1 to get an infinite family of non-isomorphic bricks of the same dimension. In case the
$i \ge 1$
. Looking at these algebras up to isomorphisms, we have either a finite family, or an infinite family. In the former case, we apply Lemma 5.1 to get an infinite family of non-isomorphic bricks of the same dimension. In case the
![]() $\Lambda /I_i$
form infinitely many non-isomorphic algebras, we have infinitely many
$\Lambda /I_i$
form infinitely many non-isomorphic algebras, we have infinitely many
![]() $\tau $
-tilting finite quotient algebras of the same dimension.
$\tau $
-tilting finite quotient algebras of the same dimension.
Recall that if
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
are functorially finite torsion classes in
$\mathcal {T}'$
are functorially finite torsion classes in
![]() $\mathrm {mod}\Lambda $
, such that
$\mathrm {mod}\Lambda $
, such that
![]() $\mathcal {T} \subsetneq \mathcal {T}'$
is a covering relation in the poset of torsion classes, then there is a unique brick
$\mathcal {T} \subsetneq \mathcal {T}'$
is a covering relation in the poset of torsion classes, then there is a unique brick
![]() $B \in \mathcal {T}'$
which satisfies the following properties:
$B \in \mathcal {T}'$
which satisfies the following properties:
-
1.
 $\mathrm {Hom}_{\Lambda }(\mathcal {T},B)=0$
.
$\mathrm {Hom}_{\Lambda }(\mathcal {T},B)=0$
. -
2. Every proper quotient of B lies in
 $\mathcal {T}$
.
$\mathcal {T}$
. -
3. Every nonsplit short exact sequence
 $0 \to B \to X \to T \to 0$
with
$0 \to B \to X \to T \to 0$
with
 $T \in \mathcal {T}$
is such that
$T \in \mathcal {T}$
is such that
 $X \in \mathcal {T}$
.
$X \in \mathcal {T}$
.
Such a module is called a minimal extending brick for
![]() $\mathcal {T}$
. This brick is used to label the edge corresponding to the covering relation
$\mathcal {T}$
. This brick is used to label the edge corresponding to the covering relation
![]() $\mathcal {T} \subsetneq \mathcal {T}'$
in the Hasse diagram of functorially finite torsion classes of
$\mathcal {T} \subsetneq \mathcal {T}'$
in the Hasse diagram of functorially finite torsion classes of
![]() $\operatorname{\mathrm{mod}} \Lambda $
. In [Reference BongartzBCZ], the authors extensively study the brick labeling of the poset of functorially finite torsion classes.
$\operatorname{\mathrm{mod}} \Lambda $
. In [Reference BongartzBCZ], the authors extensively study the brick labeling of the poset of functorially finite torsion classes.
In the poset of functorially finite torsion classes of
![]() $\Lambda $
, a torsion class
$\Lambda $
, a torsion class
![]() $\mathcal {T}$
is said to be at level at most
$\mathcal {T}$
is said to be at level at most
![]() $t \in \mathbb {N}$
if the interval
$t \in \mathbb {N}$
if the interval
![]() $[0, \mathcal {T}]$
contains a path of covering relations of length at most t. For a functorially finite torsion class
$[0, \mathcal {T}]$
contains a path of covering relations of length at most t. For a functorially finite torsion class
![]() $\mathcal {T}$
, in the next lemma, we show that the length of all extending bricks for
$\mathcal {T}$
, in the next lemma, we show that the length of all extending bricks for
![]() $\mathcal {T}$
are bounded by a function which depends only on the level of
$\mathcal {T}$
are bounded by a function which depends only on the level of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $d:=\dim _k \Lambda $
. To give a more explicit proof for the next lemma, we use a bijection from [Reference Assem, Simson and SkowrońskiAIR, §3] which relates
$d:=\dim _k \Lambda $
. To give a more explicit proof for the next lemma, we use a bijection from [Reference Assem, Simson and SkowrońskiAIR, §3] which relates
![]() $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
and the isomorphism classes of basic
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
and the isomorphism classes of basic
![]() $2$
-term silting complexes in
$2$
-term silting complexes in
![]() $K^b(\mathrm { proj}\Lambda )$
. As further shown in [Reference Assem, Simson and SkowrońskiAIR], the aforementioned bijection gives rise to a poset isomorphism between the poset of support
$K^b(\mathrm { proj}\Lambda )$
. As further shown in [Reference Assem, Simson and SkowrońskiAIR], the aforementioned bijection gives rise to a poset isomorphism between the poset of support
![]() $\tau $
-tilting modules and the poset of
$\tau $
-tilting modules and the poset of
![]() $2$
-term silting complexes coming from [Reference Angeleri Hügel, Marks and VitóriaAI]. Hence, the mutation of modules in
$2$
-term silting complexes coming from [Reference Angeleri Hügel, Marks and VitóriaAI]. Hence, the mutation of modules in
![]() $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
amounts to mutation of the corresponding
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
amounts to mutation of the corresponding
![]() $2$
-term silting complexes, where the latter is in terms of certain triangles in the bounded derived category of
$2$
-term silting complexes, where the latter is in terms of certain triangles in the bounded derived category of
![]() $\operatorname{\mathrm{mod}} \Lambda $
. Namely, if
$\operatorname{\mathrm{mod}} \Lambda $
. Namely, if
![]() $T < T'$
is a covering relation in the poset of
$T < T'$
is a covering relation in the poset of
![]() $2$
-term silting complexes in
$2$
-term silting complexes in
![]() $K^b(\mathrm {proj}\Lambda )$
, by [Reference Angeleri Hügel, Marks and VitóriaAI, Th. 2.31],
$K^b(\mathrm {proj}\Lambda )$
, by [Reference Angeleri Hügel, Marks and VitóriaAI, Th. 2.31],
![]() $T'$
is a right mutation of T at one of its indecomposable summand. More precisely, we have
$T'$
is a right mutation of T at one of its indecomposable summand. More precisely, we have
![]() $T=U \oplus X$
and
$T=U \oplus X$
and
![]() $T' = U \oplus Y$
, with U being a
$T' = U \oplus Y$
, with U being a
![]() $2$
-term presilting object and X and Y a pair of non-isomorphic indecomposable objects which appear in a triangle
$2$
-term presilting object and X and Y a pair of non-isomorphic indecomposable objects which appear in a triangle
where
![]() $U'$
is such that
$U'$
is such that
![]() $U' \to X$
is a minimal right
$U' \to X$
is a minimal right
![]() $\mathrm {add}(U)$
-approximation of X. (For full details, see [Reference Angeleri Hügel, Marks and VitóriaAI] and [Reference Assem, Simson and SkowrońskiAIR].)
$\mathrm {add}(U)$
-approximation of X. (For full details, see [Reference Angeleri Hügel, Marks and VitóriaAI] and [Reference Assem, Simson and SkowrońskiAIR].)
Lemma 5.2. Let
![]() $\mathcal {T}=\mathrm {Fac}(M)$
be a functorially finite torsion class in
$\mathcal {T}=\mathrm {Fac}(M)$
be a functorially finite torsion class in
![]() $\operatorname{\mathrm{mod}} \Lambda $
which is at level at most t, and where M is support
$\operatorname{\mathrm{mod}} \Lambda $
which is at level at most t, and where M is support
![]() $\tau $
-tilting. Then, the dimension of M as well as that of any minimal extending brick for
$\tau $
-tilting. Then, the dimension of M as well as that of any minimal extending brick for
![]() $\mathcal {T}$
is bounded by a function that depends only on t and on the dimension of
$\mathcal {T}$
is bounded by a function that depends only on t and on the dimension of
![]() $\Lambda $
.
$\Lambda $
.
Proof. Let T be a
![]() $2$
-term silting complex in
$2$
-term silting complex in
![]() $K^b(\mathrm {proj}\Lambda )$
represented by
$K^b(\mathrm {proj}\Lambda )$
represented by
![]() $P_1 \to P_0$
. We assume that the differential is a radical morphism, and hence
$P_1 \to P_0$
. We assume that the differential is a radical morphism, and hence
![]() $P_0$
and
$P_0$
and
![]() $P_1$
are uniquely determined up to isomorphism. Let
$P_1$
are uniquely determined up to isomorphism. Let
![]() $\dim T$
denote the total dimension of T, given by
$\dim T$
denote the total dimension of T, given by
![]() $\dim _k P_0+ \dim _k P_1$
.
$\dim _k P_0+ \dim _k P_1$
.
Using the same notation as in the paragraph preceding the lemma, we assume
![]() $T'$
is the right mutation of T at X. Let
$T'$
is the right mutation of T at X. Let
![]() $\dim \mathrm {Hom}(U,X)=m$
. Then we have a right
$\dim \mathrm {Hom}(U,X)=m$
. Then we have a right
![]() $\mathrm {add}(U)$
-approximation
$\mathrm {add}(U)$
-approximation
![]() $U^m \to X$
of X. It is well known that there is a direct summand of
$U^m \to X$
of X. It is well known that there is a direct summand of
![]() $U^m$
, isomorphic to
$U^m$
, isomorphic to
![]() $U'$
, such that the corresponding restriction map is minimal. This yields
$U'$
, such that the corresponding restriction map is minimal. This yields
![]() $\dim U' \le m \, \dim U$
. Observe that an upper bound for
$\dim U' \le m \, \dim U$
. Observe that an upper bound for
![]() $\dim \mathrm {Hom}(U,X)=m$
is given by
$\dim \mathrm {Hom}(U,X)=m$
is given by
![]() $\dim \mathrm { Hom}(T,T)$
, which in turn is bounded above by
$\dim \mathrm { Hom}(T,T)$
, which in turn is bounded above by
![]() $\dim \mathrm {Hom}(P_1,P_1)$
+
$\dim \mathrm {Hom}(P_1,P_1)$
+
![]() $\dim \mathrm {Hom}(P_0,P_0)$
. Now, the latter is bounded above by
$\dim \mathrm {Hom}(P_0,P_0)$
. Now, the latter is bounded above by
![]() $(\dim P_0)^2 + (\dim P_1)^2$
, which in turn does not exceed
$(\dim P_0)^2 + (\dim P_1)^2$
, which in turn does not exceed
![]() $2(\dim T)^2$
. Therefore,
$2(\dim T)^2$
. Therefore,
 $$ \begin{align*} \dim Y & \le \dim U' + \dim X \\ & \le m \, \dim U + \dim X \\ & \le (m+1) \dim T \\ & \le (2(\dim T)^2 + 1) \dim T, \end{align*} $$
$$ \begin{align*} \dim Y & \le \dim U' + \dim X \\ & \le m \, \dim U + \dim X \\ & \le (m+1) \dim T \\ & \le (2(\dim T)^2 + 1) \dim T, \end{align*} $$
and hence, as
![]() $\dim U \le \dim T$
, we get
$\dim U \le \dim T$
, we get
Note that for the minimal element of
![]() $s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, the corresponding element in the poset of
$s\tau \operatorname{-\textrm{tilt}}(\Lambda )$
, the corresponding element in the poset of
![]() $2$
-term silting complexes is
$2$
-term silting complexes is
![]() $\Lambda \to 0$
, which has total dimension
$\Lambda \to 0$
, which has total dimension
![]() $d:=\mathrm {dim}_k\Lambda $
. Let T be a
$d:=\mathrm {dim}_k\Lambda $
. Let T be a
![]() $2$
-term silting complex such that the interval
$2$
-term silting complex such that the interval
![]() $[0,T]$
in the Hasse quiver of poset of
$[0,T]$
in the Hasse quiver of poset of
![]() $2$
-term silting complexes has a path of length at most t. Then there is a function
$2$
-term silting complexes has a path of length at most t. Then there is a function
![]() $g(d,t)$
which depends only on d and t such that
$g(d,t)$
which depends only on d and t such that
![]() $\mathrm {dim}T \le g(d,t)$
. Note that this function
$\mathrm {dim}T \le g(d,t)$
. Note that this function
![]() $g(d,t)$
is polynomial of degree
$g(d,t)$
is polynomial of degree
![]() $3^t$
in d.
$3^t$
in d.
Now, let T be at level at most t and
![]() $T'$
be a right mutation of T. By [Reference Assem, Simson and SkowrońskiAIR, Th. 3.2], the support
$T'$
be a right mutation of T. By [Reference Assem, Simson and SkowrońskiAIR, Th. 3.2], the support
![]() $\tau $
-tilting module M (resp.
$\tau $
-tilting module M (resp.
![]() $M'$
) corresponding to T (resp. to
$M'$
) corresponding to T (resp. to
![]() $T'$
) is the zeroth cohomology of T (resp. of T). Thus,
$T'$
) is the zeroth cohomology of T (resp. of T). Thus,
![]() $\dim M \leq \dim T \le g(d,t)$
and
$\dim M \leq \dim T \le g(d,t)$
and
![]() $\dim M' \leq \dim T' \le g(d,t+1)$
. By [Reference Assem, Simson and SkowrońskiAIR, Ths. 2.7 and 3.2], we assume that
$\dim M' \leq \dim T' \le g(d,t+1)$
. By [Reference Assem, Simson and SkowrońskiAIR, Ths. 2.7 and 3.2], we assume that
![]() $\mathcal {T}$
denotes the functorially finite torsion class associated with T. Moreover, [Reference Assem, Simson and SkowrońskiAIR, Cors. 2.34 and 3.9] imply that
$\mathcal {T}$
denotes the functorially finite torsion class associated with T. Moreover, [Reference Assem, Simson and SkowrońskiAIR, Cors. 2.34 and 3.9] imply that
![]() $\mathcal {T}$
is at level at most t in the poset of functorially finite torsion classes of
$\mathcal {T}$
is at level at most t in the poset of functorially finite torsion classes of
![]() $\operatorname{\mathrm{mod}} \Lambda $
, with the covering relation
$\operatorname{\mathrm{mod}} \Lambda $
, with the covering relation
![]() $\mathcal {T} < \operatorname {Fac}(M')$
. Since the minimal extending brick B for the covering relation
$\mathcal {T} < \operatorname {Fac}(M')$
. Since the minimal extending brick B for the covering relation
![]() $\mathcal {T} < \operatorname {Fac}(M')$
is a quotient of
$\mathcal {T} < \operatorname {Fac}(M')$
is a quotient of
![]() $M'$
, we obviously have
$M'$
, we obviously have
![]() $\dim B \leq g(d,t+1)$
. This gives a function that bounds the dimension of all minimal extending brick for
$\dim B \leq g(d,t+1)$
. This gives a function that bounds the dimension of all minimal extending brick for
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Proposition 5.3. Let
![]() $\Lambda $
be min-
$\Lambda $
be min-
![]() $\tau $
-infinite, and let
$\tau $
-infinite, and let
![]() $\{I_i\}_{i\in A}$
be an infinite family of pairwise distinct ideals in
$\{I_i\}_{i\in A}$
be an infinite family of pairwise distinct ideals in
![]() $\Lambda $
. If each
$\Lambda $
. If each
![]() $\Lambda /I_i$
admits a faithful brick, then
$\Lambda /I_i$
admits a faithful brick, then
![]() $\operatorname{\mathrm{brick}}(\Lambda )$
has an infinite family of pairwise non-isomorphic bricks of the same dimension.
$\operatorname{\mathrm{brick}}(\Lambda )$
has an infinite family of pairwise non-isomorphic bricks of the same dimension.
Proof. Without loss of generality, assume that the family
![]() $\{I_i\}_{i\in A}$
is such that all ideals are of the same dimension, and this dimension is maximal with the property that each
$\{I_i\}_{i\in A}$
is such that all ideals are of the same dimension, and this dimension is maximal with the property that each
![]() $\Lambda /I_i$
admits a faithful brick. If infinitely many of these
$\Lambda /I_i$
admits a faithful brick. If infinitely many of these
![]() $\Lambda /I_i$
are isomorphic, apply Lemma 5.1 and we are done. Thus, assume that
$\Lambda /I_i$
are isomorphic, apply Lemma 5.1 and we are done. Thus, assume that
![]() $\Lambda /I_i$
are pairwise non-isomorphic. If
$\Lambda /I_i$
are pairwise non-isomorphic. If
![]() $V_i$
denotes a faithful brick over
$V_i$
denotes a faithful brick over
![]() $\Lambda /I_i$
, then
$\Lambda /I_i$
, then
![]() $\{V_i\}_{i\in A}$
is a family of pairwise non-isomorphic modules in
$\{V_i\}_{i\in A}$
is a family of pairwise non-isomorphic modules in
![]() $\operatorname{\mathrm{brick}}(\Lambda )$
, particularly because
$\operatorname{\mathrm{brick}}(\Lambda )$
, particularly because
![]() $V_i$
have pairwise distinct annihilators in
$V_i$
have pairwise distinct annihilators in
![]() $\Lambda $
. If there is a bound on the dimension of bricks in
$\Lambda $
. If there is a bound on the dimension of bricks in
![]() $\{V_i\}_{i\in A}$
, we are done. Thus, for the sake of contradiction, we assume that there is no bound on the dimension of
$\{V_i\}_{i\in A}$
, we are done. Thus, for the sake of contradiction, we assume that there is no bound on the dimension of
![]() $\{V_i\}_{i\in A}$
.
$\{V_i\}_{i\in A}$
.
For every functorially finite torsion class
![]() $\mathcal {T}$
at level s, by Lemma 5.2, there is a global bound on the dimension of all minimal extending bricks for
$\mathcal {T}$
at level s, by Lemma 5.2, there is a global bound on the dimension of all minimal extending bricks for
![]() $\mathcal {T}$
. We can start by picking a positive integer
$\mathcal {T}$
. We can start by picking a positive integer
![]() $d_1$
such that infinitely many of the
$d_1$
such that infinitely many of the
![]() $\Lambda /I_i$
have a brick in dimension
$\Lambda /I_i$
have a brick in dimension
![]() $d_1$
(such as
$d_1$
(such as
![]() $d_1=1$
). For each i, by
$d_1=1$
). For each i, by
![]() $\mathcal {H}_i$
, we denote the Hasse quiver of the functorially finite torsion classes in
$\mathcal {H}_i$
, we denote the Hasse quiver of the functorially finite torsion classes in
![]() $\operatorname{\mathrm{mod}} \Lambda /I_i$
. There is an arrow
$\operatorname{\mathrm{mod}} \Lambda /I_i$
. There is an arrow
![]() $\mathcal {T} \to \mathcal {T'}$
in
$\mathcal {T} \to \mathcal {T'}$
in
![]() $\mathcal {H}_i$
precisely when
$\mathcal {H}_i$
precisely when
![]() $\mathcal {T} < \mathcal {T}'$
is a covering relation. Since we assume that there is no bound on the dimension of
$\mathcal {T} < \mathcal {T}'$
is a covering relation. Since we assume that there is no bound on the dimension of
![]() $\{V_i\}_{i\in A}$
, that means from Lemma 5.2 that the
$\{V_i\}_{i\in A}$
, that means from Lemma 5.2 that the
![]() $\mathcal {H}_i$
have arbitrarily large heights.
$\mathcal {H}_i$
have arbitrarily large heights.
Claim: For a fixed dimension s, we may assume that there is a function
![]() $h(s)$
such that every path in any given
$h(s)$
such that every path in any given
![]() $\mathcal {H}_i$
has at most
$\mathcal {H}_i$
has at most
![]() $h(s)$
minimal extending bricks of dimension at most s. To prove the claim, assume otherwise. Hence, there is a dimension
$h(s)$
minimal extending bricks of dimension at most s. To prove the claim, assume otherwise. Hence, there is a dimension
![]() $s' \le s$
such that we can find paths in the
$s' \le s$
such that we can find paths in the
![]() $\mathcal {H}_i$
having arbitrarily large number of minimal extending bricks of dimension
$\mathcal {H}_i$
having arbitrarily large number of minimal extending bricks of dimension
![]() $s'$
. Note that in a given path, the minimal extending bricks are pairwise non-isomorphic. For the bricks of dimension
$s'$
. Note that in a given path, the minimal extending bricks are pairwise non-isomorphic. For the bricks of dimension
![]() $s'$
over all
$s'$
over all
![]() $\Lambda /I_i$
, if their annihilators in
$\Lambda /I_i$
, if their annihilators in
![]() $\Lambda $
form an infinite family of pairwise distinct ideals, then we are done. Therefore, we are in the case where there is an ideal J such that
$\Lambda $
form an infinite family of pairwise distinct ideals, then we are done. Therefore, we are in the case where there is an ideal J such that
![]() $\Lambda /J$
has an infinite number of non-isomorphic bricks of dimension
$\Lambda /J$
has an infinite number of non-isomorphic bricks of dimension
![]() $s'$
, and similarly we are done. This proves our claim.
$s'$
, and similarly we are done. This proves our claim.
By the claim, the number of bricks of dimension at most
![]() $d_1$
on any given path of each
$d_1$
on any given path of each
![]() $\mathcal {H}_i$
is bounded by
$\mathcal {H}_i$
is bounded by
![]() $h(d_1)$
. Pick a positive integer
$h(d_1)$
. Pick a positive integer
![]() $l_2> h(d_1)$
. We know that we have infinitely many
$l_2> h(d_1)$
. We know that we have infinitely many
![]() $\mathcal {H}_i$
, each of which having at least one path of length
$\mathcal {H}_i$
, each of which having at least one path of length
![]() $l_2$
. By the claim, for each such i,
$l_2$
. By the claim, for each such i,
![]() $\mathcal {H}_i$
admits at least one minimal extending brick of dimension bigger than
$\mathcal {H}_i$
admits at least one minimal extending brick of dimension bigger than
![]() $d_1$
. However, it follows from Lemma 5.2 that the length of a brick on a path of length
$d_1$
. However, it follows from Lemma 5.2 that the length of a brick on a path of length
![]() $l_2$
is bounded by a function that depends only on
$l_2$
is bounded by a function that depends only on
![]() $l_2$
and the dimension of
$l_2$
and the dimension of
![]() $\Lambda /I_i$
. Therefore, by the pigeonhole principle, there is a positive integer
$\Lambda /I_i$
. Therefore, by the pigeonhole principle, there is a positive integer
![]() $d_2> d_1$
such that infinitely many of the
$d_2> d_1$
such that infinitely many of the
![]() $\Lambda /I_i$
have a brick of dimension
$\Lambda /I_i$
have a brick of dimension
![]() $d_2$
. In general, for
$d_2$
. In general, for
![]() $k \ge 2$
, we pick
$k \ge 2$
, we pick
![]() $l_k> h(d_{k-1})$
and we get that there are infinitely many
$l_k> h(d_{k-1})$
and we get that there are infinitely many
![]() $\mathcal {H}_i$
having a path of length
$\mathcal {H}_i$
having a path of length
![]() $l_k$
. As argued previously, there is a positive integer
$l_k$
. As argued previously, there is a positive integer
![]() $d_k> d_{k-1}$
such that infinitely many of the
$d_k> d_{k-1}$
such that infinitely many of the
![]() $\Lambda /I_i$
have a brick of dimension
$\Lambda /I_i$
have a brick of dimension
![]() $d_k$
.
$d_k$
.
If for a given r, infinitely many of the bricks of dimension
![]() $d_r$
are faithful over the corresponding
$d_r$
are faithful over the corresponding
![]() $\Lambda /I_i$
, then we are done, as we obtain an infinite family of non-isomorphic bricks over
$\Lambda /I_i$
, then we are done, as we obtain an infinite family of non-isomorphic bricks over
![]() $\Lambda $
of the same dimension
$\Lambda $
of the same dimension
![]() $d_r$
. Fix
$d_r$
. Fix
![]() $r \ge 1$
. Assume without loss of generality that each
$r \ge 1$
. Assume without loss of generality that each
![]() $\Lambda /I_i$
has an unfaithful brick
$\Lambda /I_i$
has an unfaithful brick
![]() $B_i$
of dimension
$B_i$
of dimension
![]() $d_r$
. Let
$d_r$
. Let
![]() $J_i:=\operatorname{\mathrm{ann}}_{\Lambda }(B_i)$
, then
$J_i:=\operatorname{\mathrm{ann}}_{\Lambda }(B_i)$
, then
![]() $I_i \subsetneq J_i$
. If the ideals
$I_i \subsetneq J_i$
. If the ideals
![]() $J_i$
form an infinite family, then again, we get that the
$J_i$
form an infinite family, then again, we get that the
![]() $B_i$
form an infinite family of non-isomorphic bricks of dimension
$B_i$
form an infinite family of non-isomorphic bricks of dimension
![]() $d_r$
. We may thus assume that infinitely many of the
$d_r$
. We may thus assume that infinitely many of the
![]() $B_i$
have the same annihilator
$B_i$
have the same annihilator
![]() $J_{d_r}$
. In particular, the algebra
$J_{d_r}$
. In particular, the algebra
![]() $\Lambda /J_{d_r}$
has a faithful brick of dimension
$\Lambda /J_{d_r}$
has a faithful brick of dimension
![]() $d_r$
. We need only to consider the case where these
$d_r$
. We need only to consider the case where these
![]() $B_i$
are (almost all) isomorphic.
$B_i$
are (almost all) isomorphic.
Thus, we are left with the situation such that for each
![]() $r \ge 1$
, we have an ideal
$r \ge 1$
, we have an ideal
![]() $J_{d_r}$
with
$J_{d_r}$
with
![]() $\Lambda /J_{d_r}$
having a faithful brick of dimension
$\Lambda /J_{d_r}$
having a faithful brick of dimension
![]() $d_r$
. We may assume that infinitely many of the ideals in the family
$d_r$
. We may assume that infinitely many of the ideals in the family
![]() $\{J_{d_r}\}$
are pairwise distinct, as otherwise a proper quotient of
$\{J_{d_r}\}$
are pairwise distinct, as otherwise a proper quotient of
![]() $\Lambda $
admits infinitely many unbounded bricks, and this contradicts the fact that each
$\Lambda $
admits infinitely many unbounded bricks, and this contradicts the fact that each
![]() $\Lambda /J_{d_r}$
is
$\Lambda /J_{d_r}$
is
![]() $\tau $
-tilting finite. Now, the family
$\tau $
-tilting finite. Now, the family
![]() $\{J_{d_r}\}_{r \ge 1}$
yields an infinite family of ideals of the same dimension which are pairwise distinct and each
$\{J_{d_r}\}_{r \ge 1}$
yields an infinite family of ideals of the same dimension which are pairwise distinct and each
![]() $\Lambda /J_{d_r}$
admits a faithful brick. This gives the desired contradiction with our assumption at the beginning of the proof on the dimension of ideals in the family
$\Lambda /J_{d_r}$
admits a faithful brick. This gives the desired contradiction with our assumption at the beginning of the proof on the dimension of ideals in the family
![]() $\{I_i\}_{i \in A}$
.
$\{I_i\}_{i \in A}$
.
From the previous proposition, we obtain the following theorem.
Theorem 5.4. Let
![]() $\Lambda $
be a min-
$\Lambda $
be a min-
![]() $\tau $
-infinite algebra. If
$\tau $
-infinite algebra. If
![]() $\Lambda $
has infinitely many unfaithful bricks, then it admits an infinite family of bricks of the same length.
$\Lambda $
has infinitely many unfaithful bricks, then it admits an infinite family of bricks of the same length.
Again, we note that the situation in Lemma 5.1, Proposition 5.3, and the above theorem can occur only for nondistributive algebras. In particular, it is natural to ask whether it is true in general that a min-
![]() $\tau $
-infinite algebra
$\tau $
-infinite algebra
![]() $\Lambda $
is nondistributive if and only if
$\Lambda $
is nondistributive if and only if
![]() $\operatorname{\mathrm{brick}}(\Lambda )$
contains an infinite family of unfaithful bricks. We remark that the analogous classification holds for min-rep-infinite algebras. Namely, a min-rep-inf algebra
$\operatorname{\mathrm{brick}}(\Lambda )$
contains an infinite family of unfaithful bricks. We remark that the analogous classification holds for min-rep-infinite algebras. Namely, a min-rep-inf algebra
![]() $\Lambda $
is nondistributive if and only if
$\Lambda $
is nondistributive if and only if
![]() $\operatorname{\mathrm{ind}}(\Lambda )$
contains an infinite family of unfaithful modules. In our future work, we treat the nondistributive min-
$\operatorname{\mathrm{ind}}(\Lambda )$
contains an infinite family of unfaithful modules. In our future work, we treat the nondistributive min-
![]() $\tau $
-infinite algebras more closely.
$\tau $
-infinite algebras more closely.
6 The first Brauer–Thrall conjecture for bricks
In this short section, we use the geometric setting of representation varieties to give a new proof for the brick analogue of the first Brauer–Thrall conjecture, recently shown by Schroll and Treffinger [Reference Schroll and TreffingerST]. To do so, we prove an interesting property of the minimal extending bricks in terms of the geometry of their orbits.
Recall that if the algebra
![]() $\Lambda $
is given by a bound quiver
$\Lambda $
is given by a bound quiver
![]() $(Q,I)$
over a field k, each module in
$(Q,I)$
over a field k, each module in
![]() $\operatorname{\mathrm{mod}} \Lambda $
can be viewed as a point in a representation variety. For a fixed dimension vector
$\operatorname{\mathrm{mod}} \Lambda $
can be viewed as a point in a representation variety. For a fixed dimension vector
![]() $\mathbf {{d}}=(d_x) \in \mathbb {Z}_{\geq 0}^{Q_0}$
, we consider
$\mathbf {{d}}=(d_x) \in \mathbb {Z}_{\geq 0}^{Q_0}$
, we consider
![]() $\operatorname{\mathrm{rep}}(Q,\mathbf {d})$
the affine space given by
$\operatorname{\mathrm{rep}}(Q,\mathbf {d})$
the affine space given by
 $$ \begin{align*}\prod_{\alpha \in Q_1}\mathrm{Mat}_{\mathbf{{d}_{e(\alpha)} \times \mathbf{d}_{s(\alpha)}}}(k).\end{align*} $$
$$ \begin{align*}\prod_{\alpha \in Q_1}\mathrm{Mat}_{\mathbf{{d}_{e(\alpha)} \times \mathbf{d}_{s(\alpha)}}}(k).\end{align*} $$
This variety parameterizes the representations of
![]() $kQ$
having dimension vector
$kQ$
having dimension vector
![]() $\mathbf {d}$
. More precisely, to the point
$\mathbf {d}$
. More precisely, to the point
![]() $(V_{\alpha })_{\alpha \in Q_1}$
in
$(V_{\alpha })_{\alpha \in Q_1}$
in
![]() $\operatorname{\mathrm{rep}}(Q,\mathbf {d})$
is associated the representation M with
$\operatorname{\mathrm{rep}}(Q,\mathbf {d})$
is associated the representation M with
![]() $M_x = k^{d_x}$
and
$M_x = k^{d_x}$
and
![]() $M(\alpha ) = V_\alpha $
. Then,
$M(\alpha ) = V_\alpha $
. Then,
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
is the closed subset of
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
is the closed subset of
![]() $\operatorname{\mathrm{rep}}(Q,\mathbf {d})$
whose points correspond to the representations annihilated by I. In this way, we view
$\operatorname{\mathrm{rep}}(Q,\mathbf {d})$
whose points correspond to the representations annihilated by I. In this way, we view
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
as an affine variety. Moreover, under the well-known action of the general linear group
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
as an affine variety. Moreover, under the well-known action of the general linear group
![]() $\operatorname{\mathrm{GL}}(\mathbf {d})$
on the variety
$\operatorname{\mathrm{GL}}(\mathbf {d})$
on the variety
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
via conjugation, the isomorphism classes of
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
via conjugation, the isomorphism classes of
![]() $\Lambda $
-modules of dimension vector
$\Lambda $
-modules of dimension vector
![]() $\mathbf {d}$
are in bijection with the
$\mathbf {d}$
are in bijection with the
![]() $\operatorname{\mathrm{GL}}(\mathbf {d})$
-orbits in
$\operatorname{\mathrm{GL}}(\mathbf {d})$
-orbits in
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
. We sometimes denote
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
. We sometimes denote
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
by
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
by
![]() $\operatorname{\mathrm{rep}}(\Lambda ,\mathbf {d})$
, where
$\operatorname{\mathrm{rep}}(\Lambda ,\mathbf {d})$
, where
![]() $\Lambda =kQ/I$
. We note that the variety
$\Lambda =kQ/I$
. We note that the variety
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
is not necessarily irreducible, but has finitely many irreducible components and each such component is stable under the action of
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
is not necessarily irreducible, but has finitely many irreducible components and each such component is stable under the action of
![]() $\operatorname{\mathrm{GL}}(\mathbf {d})$
.
$\operatorname{\mathrm{GL}}(\mathbf {d})$
.
Before we state the following result, let us remark that for an arbitrary brick M with
![]() $\underline {\dim }(M)= \mathbf {d}$
, the
$\underline {\dim }(M)= \mathbf {d}$
, the
![]() $\operatorname{\mathrm{GL}}(\mathbf {d})$
-orbit of M in
$\operatorname{\mathrm{GL}}(\mathbf {d})$
-orbit of M in
![]() $\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
is not necessarily open. However, provided that
$\operatorname{\mathrm{rep}}(Q,I,\mathbf {d})$
is not necessarily open. However, provided that
![]() $\Lambda $
is a brick finite algebras, every brick has an open orbit. The next proposition gives us a nice geometric property of the minimal extending bricks defined in §5. In particular, this result is of significance over brick infinite algebras.
$\Lambda $
is a brick finite algebras, every brick has an open orbit. The next proposition gives us a nice geometric property of the minimal extending bricks defined in §5. In particular, this result is of significance over brick infinite algebras.
Theorem 6.1. Any minimal extending brick of a functorially finite torsion class has an open orbit.
Proof. Let
![]() $\mathrm {Fac}(N)$
be an arbitrary functorially finite torsion class, where N is assumed to be a basic support
$\mathrm {Fac}(N)$
be an arbitrary functorially finite torsion class, where N is assumed to be a basic support
![]() $\tau $
-tilting module corresponding to a
$\tau $
-tilting module corresponding to a
![]() $\tau $
-rigid pair
$\tau $
-rigid pair
![]() $(N,P)$
where P is projective with
$(N,P)$
where P is projective with
![]() $\operatorname {Hom}(P,N)=0$
and N is
$\operatorname {Hom}(P,N)=0$
and N is
![]() $\tau $
-tilting over its support. It follows from [Reference Demonet, Iyama, Reading, Reiten and ThomasDIR+, Prop. 4.13] that any minimal extending brick X labeling an arrow
$\tau $
-tilting over its support. It follows from [Reference Demonet, Iyama, Reading, Reiten and ThomasDIR+, Prop. 4.13] that any minimal extending brick X labeling an arrow
![]() $\mathrm {Fac}(N) \to \mathcal {T}$
lies in
$\mathrm {Fac}(N) \to \mathcal {T}$
lies in
![]() $M^{\bot } \cap ^\perp \tau M \cap P^\perp $
where M is a direct summand of N. By [Reference JassoJ2, Th. 3.8], the category
$M^{\bot } \cap ^\perp \tau M \cap P^\perp $
where M is a direct summand of N. By [Reference JassoJ2, Th. 3.8], the category
![]() $M^{\bot } \cap ^\perp \tau M \cap P^\perp $
is equivalent to the module category
$M^{\bot } \cap ^\perp \tau M \cap P^\perp $
is equivalent to the module category
![]() $\operatorname{\mathrm{mod}} A$
, for a finite-dimensional local algebra A (see also [Reference Demonet, Iyama, Reading, Reiten and ThomasDIR+, Th. 4.12b]). Hence, X is the unique brick in
$\operatorname{\mathrm{mod}} A$
, for a finite-dimensional local algebra A (see also [Reference Demonet, Iyama, Reading, Reiten and ThomasDIR+, Th. 4.12b]). Hence, X is the unique brick in
![]() $M^{\bot } \cap ^\perp \tau M \cap P^\perp $
. Let
$M^{\bot } \cap ^\perp \tau M \cap P^\perp $
. Let
![]() $\underline {\dim }(X)=\mathbf {d}$
and consider the representation variety
$\underline {\dim }(X)=\mathbf {d}$
and consider the representation variety
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Observe that the function
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Observe that the function
![]() $Y \mapsto \mathrm {dim}\operatorname {Hom}(M,Y)$
from
$Y \mapsto \mathrm {dim}\operatorname {Hom}(M,Y)$
from
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
to
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
to
![]() $\mathbb {N}$
is upper-semicontinuous. Hence, the conditions
$\mathbb {N}$
is upper-semicontinuous. Hence, the conditions
![]() $\operatorname {Hom}(M,-)=0$
defines an open set
$\operatorname {Hom}(M,-)=0$
defines an open set
![]() $U_1$
in
$U_1$
in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Similarly, the conditions
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Similarly, the conditions
![]() $\operatorname {Hom}(-,\tau M)=0$
and
$\operatorname {Hom}(-,\tau M)=0$
and
![]() $\operatorname {Hom}(P,-)=0$
also define respective open sets
$\operatorname {Hom}(P,-)=0$
also define respective open sets
![]() $U_2$
and
$U_2$
and
![]() $U_3$
in
$U_3$
in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Therefore,
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Therefore,
![]() $U:=U_1 \cap U_2 \cap U_3$
is a nonempty open set which contains X. Furthermore, let
$U:=U_1 \cap U_2 \cap U_3$
is a nonempty open set which contains X. Furthermore, let
![]() $\operatorname{\mathrm{brick}}(\Lambda , \mathbf {d})$
denote the set of bricks in
$\operatorname{\mathrm{brick}}(\Lambda , \mathbf {d})$
denote the set of bricks in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Note that the orbit of a representation B in
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
. Note that the orbit of a representation B in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
is of dimension
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
is of dimension
![]() $\mathrm {dim} \operatorname{\mathrm{GL}}(\mathbf {d}) - \mathrm { dim} \mathrm {End}(B)$
, and hence of maximal dimension when B is a brick. Hence, it follows that
$\mathrm {dim} \operatorname{\mathrm{GL}}(\mathbf {d}) - \mathrm { dim} \mathrm {End}(B)$
, and hence of maximal dimension when B is a brick. Hence, it follows that
![]() $\operatorname{\mathrm{brick}}(\Lambda , \mathbf {d})$
also forms an open set in
$\operatorname{\mathrm{brick}}(\Lambda , \mathbf {d})$
also forms an open set in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
, since the map that associates to a representation in
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
, since the map that associates to a representation in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
the dimension of its orbit is upper-semi-continuous. Consequently, we have a nonempty open set
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
the dimension of its orbit is upper-semi-continuous. Consequently, we have a nonempty open set
![]() $U\cap \operatorname{\mathrm{brick}}(\Lambda , \mathbf {d})$
in
$U\cap \operatorname{\mathrm{brick}}(\Lambda , \mathbf {d})$
in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
which consists of bricks. However, as mentioned above, X is the unique brick in
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
which consists of bricks. However, as mentioned above, X is the unique brick in
![]() $M^{\bot } \cap ^\perp \tau M \cap P^\perp $
, which implies that the orbit of X must be open in
$M^{\bot } \cap ^\perp \tau M \cap P^\perp $
, which implies that the orbit of X must be open in
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
.
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
.
If a one-parameter family of bricks means an irreducible curve of non-isomorphic bricks in the representation variety, the above proposition yields that none of the bricks in a one-parameter family of bricks can occur as a minimal extending brick.
Using the above proposition, we give an easy proof for the following theorem, which could be viewed as a modern analogue of the first Brauer–Thrall conjecture. This result has been first shown in [Reference Schroll and TreffingerST] with no assumption on the ground field.
Theorem 6.2. An algebra
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting infinite if and only if there is no bound on the length of bricks in
$\tau $
-tilting infinite if and only if there is no bound on the length of bricks in
![]() $\operatorname{\mathrm{mod}} \Lambda $
.
$\operatorname{\mathrm{mod}} \Lambda $
.
Proof. We only show the necessity, as the sufficiency follows directly from Theorem 2.1. In the Hasse diagram of the functorially finite torsion classes of
![]() $\Lambda $
, consider an infinite path starting at the minimal element. The corresponding minimal extending bricks form an infinite family of pairwise non-isomorphic bricks. We know that, for each dimension vector
$\Lambda $
, consider an infinite path starting at the minimal element. The corresponding minimal extending bricks form an infinite family of pairwise non-isomorphic bricks. We know that, for each dimension vector
![]() $\mathbf {d}$
, the variety
$\mathbf {d}$
, the variety
![]() $\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
has only finitely many irreducible components, and the closure of each open orbit provides an irreducible component. Hence, Proposition 6.1 implies that for each
$\operatorname{\mathrm{rep}}(\Lambda , \mathbf {d})$
has only finitely many irreducible components, and the closure of each open orbit provides an irreducible component. Hence, Proposition 6.1 implies that for each
![]() $\mathbf {d}$
there are only finitely many minimal extending bricks whose dimension vector is
$\mathbf {d}$
there are only finitely many minimal extending bricks whose dimension vector is
![]() $\mathbf {d}$
. Now, the desired result is immediate.
$\mathbf {d}$
. Now, the desired result is immediate.
Acknowledgments
Mousavand would like to thank Pierre-Guy Plamondon for his hospitality and several stimulating discussions during a
![]() $3$
-month visit to Université Paris-Sud XI. Moreover, he expresses gratitudes to the organizers of the trimester program on Representation Theory at the Institut Henri Poincaré, held in 2020, where he developed part of this project. We also thank the referee for the comments, which led to an improved version of this paper.
$3$
-month visit to Université Paris-Sud XI. Moreover, he expresses gratitudes to the organizers of the trimester program on Representation Theory at the Institut Henri Poincaré, held in 2020, where he developed part of this project. We also thank the referee for the comments, which led to an improved version of this paper.