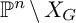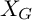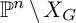1 Introduction
Let X be an algebraic variety over a finite field
![]() $\mathbb {F}_q$
of characteristic
$\mathbb {F}_q$
of characteristic
![]() $p>0$
. The zeta function of X is defined to be the following exponential sum:
$p>0$
. The zeta function of X is defined to be the following exponential sum:
 $$ \begin{align*} Z(X/\mathbb{F}_q,t):=\exp\left(\sum_{s\geq0}\frac{N_s}{s}t^s\right), \end{align*} $$
$$ \begin{align*} Z(X/\mathbb{F}_q,t):=\exp\left(\sum_{s\geq0}\frac{N_s}{s}t^s\right), \end{align*} $$
where
![]() $N_s$
is the number of
$N_s$
is the number of
![]() $\mathbb {F}_{q^s}$
-rational points of X. This function is known to be a rational function in t with coefficients in
$\mathbb {F}_{q^s}$
-rational points of X. This function is known to be a rational function in t with coefficients in
![]() $\mathbb {Z}$
by Dwork [Reference Dwork13]. For a projective hypersurface X, Dwork expressed the zeta function of X as an alternating product of characteristic polynomials of a suitably chosen representative of a Frobenius action in a series of articles [Reference Dwork14]–[Reference Dwork17], following his proof of the rationality of zeta functions. Based on Dwork’s theory, Adolphson and Sperber developed a cohomology theory and got an estimate for the zeta function when X is a closed subvariety of
$\mathbb {Z}$
by Dwork [Reference Dwork13]. For a projective hypersurface X, Dwork expressed the zeta function of X as an alternating product of characteristic polynomials of a suitably chosen representative of a Frobenius action in a series of articles [Reference Dwork14]–[Reference Dwork17], following his proof of the rationality of zeta functions. Based on Dwork’s theory, Adolphson and Sperber developed a cohomology theory and got an estimate for the zeta function when X is a closed subvariety of
![]() $\mathbb {A}^r\times \mathbb {G}_m^s$
in [Reference Adolphson and Sperber1], and when X is a smooth projective complete intersection in [Reference Adolphson and Sperber4], [Reference Adolphson and Sperber5].
$\mathbb {A}^r\times \mathbb {G}_m^s$
in [Reference Adolphson and Sperber1], and when X is a smooth projective complete intersection in [Reference Adolphson and Sperber4], [Reference Adolphson and Sperber5].
On the other hand, Monsky and Washnitzer developed rather an intrinsic cohomology theory in [Reference Monsky and Washnitzer29] when X is a smooth affine variety admitting a nice p-adic lift. Then Monsky proved the Lefschetz fixed-point theorem in [Reference Monsky25], [Reference Monsky27] to express the zeta function of X as an alternating product of characteristic polynomials of a Frobenius action on Monsky–Washnitzer cohomology. Later, van der Put [Reference Van der Put32] removed the technical condition on X assumed by Monsky and Washnitzer to make the theory work for every smooth affine variety X over
![]() $\mathbb {F}_q$
. Berthelot [Reference Berthelot9] extended this theory to not necessarily affine varieties, and the resulting theory is called rigid cohomology theory.
$\mathbb {F}_q$
. Berthelot [Reference Berthelot9] extended this theory to not necessarily affine varieties, and the resulting theory is called rigid cohomology theory.
Since Dwork cohomology and rigid cohomology compute the same important invariant, one may ask whether there is a connection between the two theories. For smooth hypersurfaces in projective spaces, Katz answered this question in [Reference Katz19]. It is strongly believed that the corresponding comparison results hold for more general cases, but up to the best of author’s knowledge, there is no written proof so the author hope that this article provides a detailed proof for general cases with several equations.
Let us briefly explain the contents of [Reference Katz19]. Let
![]() $\Bbbk /\mathbb {Q}_p$
be a finite extension with the valuation ring
$\Bbbk /\mathbb {Q}_p$
be a finite extension with the valuation ring
![]() $\mathcal {O}_{\Bbbk }$
. Given a homogeneous polynomial
$\mathcal {O}_{\Bbbk }$
. Given a homogeneous polynomial
![]() $G\in \mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
of degree
$G\in \mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
of degree
![]() $d\geq 1$
, consider a
$d\geq 1$
, consider a
![]() $\Bbbk $
-linear span of some monomials (cf. [Reference Katz19, p. 77]):
$\Bbbk $
-linear span of some monomials (cf. [Reference Katz19, p. 77]):
 $$ \begin{align*} \mathscr{L}^{0,+}:=\left\{\sum_{(u,v)\in\mathbb{Z}_{\geq0}^{\oplus n+2}}a_{u,v}x^uy^v\in\mathcal{O}_{\Bbbk}[x,y]\ \middle|\ \begin{array}{c} vd=u_0+\cdots+u_n, \\ a_{u,0}=0 \end{array}\right\}. \end{align*} $$
$$ \begin{align*} \mathscr{L}^{0,+}:=\left\{\sum_{(u,v)\in\mathbb{Z}_{\geq0}^{\oplus n+2}}a_{u,v}x^uy^v\in\mathcal{O}_{\Bbbk}[x,y]\ \middle|\ \begin{array}{c} vd=u_0+\cdots+u_n, \\ a_{u,0}=0 \end{array}\right\}. \end{align*} $$
For a fixed constant
![]() $\gamma \in \Bbbk $
, there are differential operators on
$\gamma \in \Bbbk $
, there are differential operators on
![]() $\mathscr {L}^{0,+}$
:
$\mathscr {L}^{0,+}$
:
 $$ \begin{align*} D_{x_i}:=\exp(-\gamma yG)\circ x_i\frac{\partial}{\partial x_i}\circ\exp(\gamma yG)=x_i\frac{\partial}{\partial x_i}+\gamma yx_i\frac{\partial G}{\partial x_i}, \end{align*} $$
$$ \begin{align*} D_{x_i}:=\exp(-\gamma yG)\circ x_i\frac{\partial}{\partial x_i}\circ\exp(\gamma yG)=x_i\frac{\partial}{\partial x_i}+\gamma yx_i\frac{\partial G}{\partial x_i}, \end{align*} $$
 $$ \begin{align*} D_y:=\exp(-\gamma yG)\circ y\frac{\partial}{\partial y}\circ\exp(\gamma yG)=y\frac{\partial}{\partial y}+\gamma yG. \end{align*} $$
$$ \begin{align*} D_y:=\exp(-\gamma yG)\circ y\frac{\partial}{\partial y}\circ\exp(\gamma yG)=y\frac{\partial}{\partial y}+\gamma yG. \end{align*} $$
On the other hand, suppose that the hypersurface
![]() $X_G\subseteq \mathbb {P}^n_{\Bbbk }$
defined by G is smooth. If
$X_G\subseteq \mathbb {P}^n_{\Bbbk }$
defined by G is smooth. If
![]() $H_i\subseteq \mathbb {P}^n_{\Bbbk }$
is the hyperplane defined by
$H_i\subseteq \mathbb {P}^n_{\Bbbk }$
is the hyperplane defined by
![]() $x_i=0$
for
$x_i=0$
for
![]() $i=0,\ldots ,n$
, and
$i=0,\ldots ,n$
, and
![]() $X_G^{\emptyset }:=X_G\setminus (H_0\cup \cdots \cup H_n)$
, then, by [Reference Katz19, Th. 1.16], there is an exact sequence
$X_G^{\emptyset }:=X_G\setminus (H_0\cup \cdots \cup H_n)$
, then, by [Reference Katz19, Th. 1.16], there is an exact sequence

where the local description of
![]() $\Theta $
is given in [Reference Katz19, Th. I]. Here,
$\Theta $
is given in [Reference Katz19, Th. I]. Here,
![]() $H_{\mathrm {dR}}^{\bullet }$
denotes algebraic de Rham cohomology. One way of getting a global description of
$H_{\mathrm {dR}}^{\bullet }$
denotes algebraic de Rham cohomology. One way of getting a global description of
![]() $\Theta $
is using the complement of
$\Theta $
is using the complement of
![]() $X_G$
. Namely, denote
$X_G$
. Namely, denote
![]() $\mathbb {T}^n_{\Bbbk }:=\mathbb {P}^n_{\Bbbk }\setminus (H_0\cup \cdots \cup H_n)$
with local coordinates
$\mathbb {T}^n_{\Bbbk }:=\mathbb {P}^n_{\Bbbk }\setminus (H_0\cup \cdots \cup H_n)$
with local coordinates
![]() $t_i:=x_i/x_0$
for
$t_i:=x_i/x_0$
for
![]() $i=1,\ldots ,n$
. Then there is a
$i=1,\ldots ,n$
. Then there is a
![]() $\Bbbk $
-linear map given by (cf. [Reference Katz19, p. 78])
$\Bbbk $
-linear map given by (cf. [Reference Katz19, p. 78])

inducing an exact sequence (cf. [Reference Katz19, p. 79])

Here, the map is defined via the inhomogeneous coordinates of
![]() $\mathbb {P}^n_{\Bbbk }\setminus H_0$
. One gets a description in the homogeneous coordinates using the relation:
$\mathbb {P}^n_{\Bbbk }\setminus H_0$
. One gets a description in the homogeneous coordinates using the relation:
 $$ \begin{align*} \frac{dt_1}{t_1}\wedge\cdots\wedge\frac{dt_n}{t_n}=\sum_{i=0}^n(-1)^i\frac{dx_0}{x_0}\wedge\cdots\wedge\widehat{\frac{dx_i}{x_i}}\wedge\cdots\wedge\frac{dx_n}{x_n}. \end{align*} $$
$$ \begin{align*} \frac{dt_1}{t_1}\wedge\cdots\wedge\frac{dt_n}{t_n}=\sum_{i=0}^n(-1)^i\frac{dx_0}{x_0}\wedge\cdots\wedge\widehat{\frac{dx_i}{x_i}}\wedge\cdots\wedge\frac{dx_n}{x_n}. \end{align*} $$
To relate
![]() $\mathscr {R}$
and
$\mathscr {R}$
and
![]() $\Theta $
, we use the canonical exact sequence:
$\Theta $
, we use the canonical exact sequence:
where
![]() $\mathrm {Res}_G$
is the residue map uniquely characterized by the property
$\mathrm {Res}_G$
is the residue map uniquely characterized by the property
 $$ \begin{align*} \mathrm{Res}_G\left(\frac{dG}{G}\wedge\omega\right)=\omega. \end{align*} $$
$$ \begin{align*} \mathrm{Res}_G\left(\frac{dG}{G}\wedge\omega\right)=\omega. \end{align*} $$
Then, by [Reference Katz19, Th. 1.18],
![]() $\mathrm {Res}_G\circ \mathscr {R}=\Theta $
. The remaining part of [Reference Katz19] is dedicated to compute representatives of Frobenius actions. To achieve this, we need to develop a p-adic analytic theory. Then
$\mathrm {Res}_G\circ \mathscr {R}=\Theta $
. The remaining part of [Reference Katz19] is dedicated to compute representatives of Frobenius actions. To achieve this, we need to develop a p-adic analytic theory. Then
![]() $\Theta $
and
$\Theta $
and
![]() $\mathscr {R}$
extend by continuity, and they are compatible with the Frobenius actions in a suitable sense. Since we discuss the corresponding version of the p-adic analytic theory in this article, we do not explain the remaining part of [Reference Katz19].
$\mathscr {R}$
extend by continuity, and they are compatible with the Frobenius actions in a suitable sense. Since we discuss the corresponding version of the p-adic analytic theory in this article, we do not explain the remaining part of [Reference Katz19].
Monsky’s lecture note [Reference Monsky26] gave a more detailed discussion of the algebraic version of the Dwork complex in p-adic setting together with its relations with algebraic de Rham cohomology and Monsky–Washnitzer cohomology. Then the complex algebraic analog of Dwork theory together with the connection of de Rham cohomology has been studied. Adolphson and Sperber dealt with the smooth complete intersections in affine varieties in [Reference Adolphson and Sperber3]. Dimca, Maaref, Sabbah, and Saito studied the singular subvarieties embedded in smooth varieties in [Reference Dimca, Maaref, Sabbah and Saito12] using the theory of algebraic
![]() $\mathcal {D}$
-modules. These results were again implemented in the rigid setting by Baldassarri and Berthelot for singular projective hypersurfaces in [Reference Baldassarri and Berthelot7] using the theory of arithmetic
$\mathcal {D}$
-modules. These results were again implemented in the rigid setting by Baldassarri and Berthelot for singular projective hypersurfaces in [Reference Baldassarri and Berthelot7] using the theory of arithmetic
![]() $\mathcal {D}$
-modules. On the other hand, Bourgeois [Reference Bourgeois11] directly constructed a quasi-isomorphism between the Dwork complex used by Adolphson and Sperber in [Reference Adolphson and Sperber1] and the complex of Monsky and Washnitzer in the smooth affine setting.
$\mathcal {D}$
-modules. On the other hand, Bourgeois [Reference Bourgeois11] directly constructed a quasi-isomorphism between the Dwork complex used by Adolphson and Sperber in [Reference Adolphson and Sperber1] and the complex of Monsky and Washnitzer in the smooth affine setting.
The goal of this article is to construct an explicit comparison between the Dwork cohomology of given homogeneous polynomials and the rigid cohomology of the complement of their common zero in a projective space, together with Frobenius actions defined on both sides. This generalizes the complement comparison result in [Reference Katz19] described above, but with a different choice of cochain complexes. Note that if the given homogeneous polynomials define a smooth complete intersection, then we can recover the essential information of the rigid cohomology of the common zero. The more detailed exposition will be given in the following two subsections.
As mentioned before, Adolphson and Sperber studied Dwork complexes in various settings, and it seems that the Dwork complex which appears in this article resembles the one in [Reference Adolphson and Sperber5]. Our academic contribution is to find a correct version of the p-adic Dwork complex which is appropriate to construct the desired comparison map, and give a systematic treatment of getting a connection between the two theories via the Cayley trickFootnote 1 as the author did in [Reference Park and Park31, Reference Kim, Park and Park22] to study the period integrals in the complex geometric setting.
1.1 The idea and motivation
One remarkable observation so far is that the comparison becomes more transparent when we consider the complement of the hypersurface X in the ambient projective space
![]() $\mathbb {P}^n_{\mathbb {F}_q}$
. Moreover, we may extract information of
$\mathbb {P}^n_{\mathbb {F}_q}$
. Moreover, we may extract information of
![]() $H_{\mathrm {rig}}^{\bullet }(X)$
from
$H_{\mathrm {rig}}^{\bullet }(X)$
from
![]() $H_{\mathrm {rig}}^{\bullet }(\mathbb {P}^n_{\mathbb {F}_q}\setminus X)$
, where
$H_{\mathrm {rig}}^{\bullet }(\mathbb {P}^n_{\mathbb {F}_q}\setminus X)$
, where
![]() $H_{\mathrm {rig}}^{\bullet }$
denotes rigid cohomology. Indeed, if
$H_{\mathrm {rig}}^{\bullet }$
denotes rigid cohomology. Indeed, if
![]() $X\subseteq Y$
is a codimension k closed embedding of smooth varieties over
$X\subseteq Y$
is a codimension k closed embedding of smooth varieties over
![]() $\mathbb {F}_q$
, then there is a commutative diagram with exact rows:
$\mathbb {F}_q$
, then there is a commutative diagram with exact rows:

where the top row is a special case of the excision exact sequence [Reference Berthelot10, Prop. 2.5], and the isomorphisms in the columns come from the Gysin isomorphism [Reference Le Stum23, §9.3]. Therefore, if
![]() $X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
is a smooth projective complete intersection given by homogeneous polynomials
$X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
is a smooth projective complete intersection given by homogeneous polynomials
![]() $\overline {G}_1,\ldots ,\overline {G}_k\in \mathbb {F}_q[x_0,\ldots ,x_n]$
, then there is a long exact sequence, called the Gysin exact sequence:
$\overline {G}_1,\ldots ,\overline {G}_k\in \mathbb {F}_q[x_0,\ldots ,x_n]$
, then there is a long exact sequence, called the Gysin exact sequence:

which is a rigid cohomology analog of the excision exact sequence of algebraic de Rham cohomology. As in the case of algebraic de Rham cohomology, this sequence induces an isomorphism
where
![]() $H_{\mathrm {prim}}^{n-k}(X_{\overline {G}})$
is the primitive part of
$H_{\mathrm {prim}}^{n-k}(X_{\overline {G}})$
is the primitive part of
![]() $H_{\mathrm {rig}}^{n-k}(X_{\overline {G}})$
. Using the interpretation of the zeta function as the characteristic polynomial of the Frobenius action on the cohomology (see, e.g., [Reference Étesse and Le Stum18]), one can deduce that the zeta function of
$H_{\mathrm {rig}}^{n-k}(X_{\overline {G}})$
. Using the interpretation of the zeta function as the characteristic polynomial of the Frobenius action on the cohomology (see, e.g., [Reference Étesse and Le Stum18]), one can deduce that the zeta function of
![]() $X_{\overline {G}}$
can be written as
$X_{\overline {G}}$
can be written as
 $$ \begin{align*} Z(X_{\overline{G}}/\mathbb{F}_q,t)=\frac{P(t)^{(-1)^{n-k-1}}}{(1-t)(1-qt)\ldots(1-q^{n-k}t)} \end{align*} $$
$$ \begin{align*} Z(X_{\overline{G}}/\mathbb{F}_q,t)=\frac{P(t)^{(-1)^{n-k-1}}}{(1-t)(1-qt)\ldots(1-q^{n-k}t)} \end{align*} $$
and
![]() $P(t)$
is completely determined by the Frobenius action on the primitive part. Hence, the computation of the cohomology of the projective complement has its own importance. Once we decide to focus on the cohomology of the complement, we may forget about the regularity of
$P(t)$
is completely determined by the Frobenius action on the primitive part. Hence, the computation of the cohomology of the projective complement has its own importance. Once we decide to focus on the cohomology of the complement, we may forget about the regularity of
![]() $X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
because
$X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
because
![]() $\mathbb {P}^n_{\mathbb {F}_q}\setminus X_{\overline {G}}$
is always smooth, being an open subset of the smooth space
$\mathbb {P}^n_{\mathbb {F}_q}\setminus X_{\overline {G}}$
is always smooth, being an open subset of the smooth space
![]() $\mathbb {P}^n_{\mathbb {F}_q}$
.
$\mathbb {P}^n_{\mathbb {F}_q}$
.
On the other hand, the Dwork complex can be defined for any homogeneous polynomials
![]() $\overline {G}_1,\ldots ,\overline {G}_k\in \mathbb {F}_q[x_0,\ldots ,x_n]$
, regardless of the regularity of their common zero
$\overline {G}_1,\ldots ,\overline {G}_k\in \mathbb {F}_q[x_0,\ldots ,x_n]$
, regardless of the regularity of their common zero
![]() $X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
. Namely, taking the Teichmüller lifts of the coefficients of each
$X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
. Namely, taking the Teichmüller lifts of the coefficients of each
![]() $\overline {G}_i$
, we get homogeneous polynomials
$\overline {G}_i$
, we get homogeneous polynomials
![]() $G_i$
defined over some finite extension
$G_i$
defined over some finite extension
![]() $\Bbbk /\mathbb {Q}_p$
with
$\Bbbk /\mathbb {Q}_p$
with
![]() $\deg G_i=\deg \overline {G}_i$
such that the reduction of each
$\deg G_i=\deg \overline {G}_i$
such that the reduction of each
![]() $G_i$
becomes
$G_i$
becomes
![]() $\overline {G}_i$
. Then, we define the Dwork complex associated with
$\overline {G}_i$
. Then, we define the Dwork complex associated with
![]() $\overline {G}_1,\ldots ,\overline {G}_k$
to be the twisted de Rham complex of the form
$\overline {G}_1,\ldots ,\overline {G}_k$
to be the twisted de Rham complex of the form
where
![]() $\Bbbk \{x,\hbar y\}$
is the Tate algebra over
$\Bbbk \{x,\hbar y\}$
is the Tate algebra over
![]() $\Bbbk $
(see Definition 4.8), and
$\Bbbk $
(see Definition 4.8), and
![]() $\hbar ,\gamma \in \Bbbk ^{\times }$
are some parameters.
$\hbar ,\gamma \in \Bbbk ^{\times }$
are some parameters.
Although the Dwork complex is defined for homogeneous polynomials, its cohomology would depend only on their common zero locus. For example, when we are working with one homogeneous polynomial
![]() $\overline {G}\in \mathbb {F}_q[x_0,\ldots ,x_n]$
, there are comparison theorems between the Dwork cohomology of
$\overline {G}\in \mathbb {F}_q[x_0,\ldots ,x_n]$
, there are comparison theorems between the Dwork cohomology of
![]() $\overline {G}$
and the rigid cohomology of
$\overline {G}$
and the rigid cohomology of
![]() $\mathbb {P}^n_{\mathbb {F}_q}\setminus X_{\overline {G}}$
. In the existing results, [Reference Katz19] and [Reference Baldassarri and Berthelot7], they remove the hyperplane divisors in
$\mathbb {P}^n_{\mathbb {F}_q}\setminus X_{\overline {G}}$
. In the existing results, [Reference Katz19] and [Reference Baldassarri and Berthelot7], they remove the hyperplane divisors in
![]() $\mathbb {P}^n_{\mathbb {F}_q}$
defined by
$\mathbb {P}^n_{\mathbb {F}_q}$
defined by
![]() $x_0,\ldots ,x_n$
to get an affine open subset, where one can write down a comparison map, and then use the log de Rham complex to recover the original situation. Consequently, their Dwork complexes are exactly the ones defined by Adolphson and Sperber in [Reference Adolphson and Sperber2, §2].
$x_0,\ldots ,x_n$
to get an affine open subset, where one can write down a comparison map, and then use the log de Rham complex to recover the original situation. Consequently, their Dwork complexes are exactly the ones defined by Adolphson and Sperber in [Reference Adolphson and Sperber2, §2].
Instead of removing hyperplane divisors in
![]() $\mathbb {P}^n_{\mathbb {F}_q}$
, we use the Cayley trick to convert the computation involving polynomials to the computation involving a hypersurface contained in a larger space. With the above notation, the hypersurface is cut out by
$\mathbb {P}^n_{\mathbb {F}_q}$
, we use the Cayley trick to convert the computation involving polynomials to the computation involving a hypersurface contained in a larger space. With the above notation, the hypersurface is cut out by
![]() $y_1G_1+\cdots +y_kG_k$
in a projective bundle
$y_1G_1+\cdots +y_kG_k$
in a projective bundle
![]() $\mathbb {P}(\mathcal {E})\rightarrow \mathbb {P}^n_{\Bbbk }$
for a suitably chosen locally free
$\mathbb {P}(\mathcal {E})\rightarrow \mathbb {P}^n_{\Bbbk }$
for a suitably chosen locally free
![]() $\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}$
-module
$\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}$
-module
![]() $\mathcal {E}$
of finite rank, where
$\mathcal {E}$
of finite rank, where
![]() $y_1,\ldots ,y_k$
play the role of fiber coordinates. Consequently, we get the Dwork complex as in (1.2) which resembles Adolphson and Sperber’s Dwork complex defined in [Reference Adolphson and Sperber5, §2]. The difference of our Dwork complex and the one in [Reference Adolphson and Sperber5] comes from the different choice of Dwork’s splitting functions (for a definition, see §5), which causes the different choice of the lift of
$y_1,\ldots ,y_k$
play the role of fiber coordinates. Consequently, we get the Dwork complex as in (1.2) which resembles Adolphson and Sperber’s Dwork complex defined in [Reference Adolphson and Sperber5, §2]. The difference of our Dwork complex and the one in [Reference Adolphson and Sperber5] comes from the different choice of Dwork’s splitting functions (for a definition, see §5), which causes the different choice of the lift of
![]() $y_1\overline {G}_1+\cdots +y_k\overline {G}_k\in \mathbb {F}_q[x_0,\ldots ,x_n]$
over the p-adic field. Since the lift of Adolphson and Sperber, denoted by H in [Reference Adolphson and Sperber5, eq. (2.10)], is a power series in
$y_1\overline {G}_1+\cdots +y_k\overline {G}_k\in \mathbb {F}_q[x_0,\ldots ,x_n]$
over the p-adic field. Since the lift of Adolphson and Sperber, denoted by H in [Reference Adolphson and Sperber5, eq. (2.10)], is a power series in
![]() $y_1,\ldots ,y_k$
, it does not define a hyperplane in
$y_1,\ldots ,y_k$
, it does not define a hyperplane in
![]() $\mathbb {P}(\mathcal {E})$
. Hence, we cannot get the desired geometric object. However, our lift
$\mathbb {P}(\mathcal {E})$
. Hence, we cannot get the desired geometric object. However, our lift
![]() $y_1G_1+\cdots +y_kG_k$
is linear in
$y_1G_1+\cdots +y_kG_k$
is linear in
![]() $y_1,\ldots ,y_k$
so it indeed define a hypersurface in
$y_1,\ldots ,y_k$
so it indeed define a hypersurface in
![]() $\mathbb {P}(\mathcal {E})$
. Although the two Dwork complexes are different, their reductions on the finite field are exactly the same so one may expect that both Dwork complexes have the same cohomology. This is true when
$\mathbb {P}(\mathcal {E})$
. Although the two Dwork complexes are different, their reductions on the finite field are exactly the same so one may expect that both Dwork complexes have the same cohomology. This is true when
![]() $\overline {G}_1,\ldots ,\overline {G}_k$
defines a smooth projective complete intersection in
$\overline {G}_1,\ldots ,\overline {G}_k$
defines a smooth projective complete intersection in
![]() $\mathbb {P}^n_{\mathbb {F}_q}$
(see Remark 4.13). Hence, the two Dwork complexes may be regarded as equivalent at least for this case.
$\mathbb {P}^n_{\mathbb {F}_q}$
(see Remark 4.13). Hence, the two Dwork complexes may be regarded as equivalent at least for this case.
1.2 The main results
Let
![]() $\Bbbk /\mathbb {Q}_p$
be a finite extension with the valuation ring
$\Bbbk /\mathbb {Q}_p$
be a finite extension with the valuation ring
![]() $(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })$
. Denote
$(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })$
. Denote
![]() $\mathrm {val}_p$
the p-adic valuation such that
$\mathrm {val}_p$
the p-adic valuation such that
![]() $\mathrm {val}_p(p)=1$
. Given homogeneous polynomials
$\mathrm {val}_p(p)=1$
. Given homogeneous polynomials
![]() $G_1,\ldots ,G_k\in \mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
of positive degrees
$G_1,\ldots ,G_k\in \mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
of positive degrees
![]() $d_1,\ldots ,d_k$
not divisible by the uniformizer of
$d_1,\ldots ,d_k$
not divisible by the uniformizer of
![]() $\mathcal {O}_{\Bbbk }$
, we introduce formal variables
$\mathcal {O}_{\Bbbk }$
, we introduce formal variables
![]() $y_1,\ldots ,y_k$
corresponding to
$y_1,\ldots ,y_k$
corresponding to
![]() $G_1,\ldots ,G_k$
so that the polynomial
$G_1,\ldots ,G_k$
so that the polynomial
defines a hypersurface in an affine space. Consider the twisted de Rham complex
where
![]() $\hbar ,\gamma \in \mathcal {O}_{\Bbbk }$
are regarded as parameters. Introduce gradings
$\hbar ,\gamma \in \mathcal {O}_{\Bbbk }$
are regarded as parameters. Introduce gradings
 $$ \begin{align} \left\{\begin{array}{@{}ll} \deg_cx_i:=1 & i=0,\ldots,n, \\ \deg_cy_j:=-d_j & j=1,\ldots,k, \\ \deg_cdx_i:=1 & i=0,\ldots,n, \\ \deg_cdy_j:=-d_j & j=1,\ldots,k, \end{array} \right. \quad\quad \left\{\begin{array}{@{}ll} \deg_wx_i:=0 & i=0,\ldots,n, \\ \deg_wy_j:=1 & j=1,\ldots,k, \\ \deg_wdx_i:=0 & i=0,\ldots,n, \\ \deg_wdy_j:=1 & j=1,\ldots,k, \end{array} \right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{@{}ll} \deg_cx_i:=1 & i=0,\ldots,n, \\ \deg_cy_j:=-d_j & j=1,\ldots,k, \\ \deg_cdx_i:=1 & i=0,\ldots,n, \\ \deg_cdy_j:=-d_j & j=1,\ldots,k, \end{array} \right. \quad\quad \left\{\begin{array}{@{}ll} \deg_wx_i:=0 & i=0,\ldots,n, \\ \deg_wy_j:=1 & j=1,\ldots,k, \\ \deg_wdx_i:=0 & i=0,\ldots,n, \\ \deg_wdy_j:=1 & j=1,\ldots,k, \end{array} \right. \end{align} $$
so that S and
![]() $dS$
become homogeneous of bidegree
$dS$
become homogeneous of bidegree
![]() $(\deg _c,\deg _w)=(0,1)$
and the twisted de Rham complex is graded with respect to
$(\deg _c,\deg _w)=(0,1)$
and the twisted de Rham complex is graded with respect to
![]() $\deg _c$
. Then the Dwork complex associated with
$\deg _c$
. Then the Dwork complex associated with
![]() $G_1,\ldots ,G_k$
will be defined by
$G_1,\ldots ,G_k$
will be defined by
where
![]() $\Bbbk \{x,\hbar y\}$
will be a version of the Tate algebra (see Remark 4.9).
$\Bbbk \{x,\hbar y\}$
will be a version of the Tate algebra (see Remark 4.9).
On the other hand, denote
![]() $C_S^{\dagger }:=\mathcal {O}_{\Bbbk }\{x,y,S^{-1}\}^{\dagger }$
the weak completion (see Definition 4.1 or [Reference Monsky and Washnitzer29, Th. 2.3]) of
$C_S^{\dagger }:=\mathcal {O}_{\Bbbk }\{x,y,S^{-1}\}^{\dagger }$
the weak completion (see Definition 4.1 or [Reference Monsky and Washnitzer29, Th. 2.3]) of
![]() $\mathcal {O}_{\Bbbk }[x,y,S^{-1}]$
, and
$\mathcal {O}_{\Bbbk }[x,y,S^{-1}]$
, and
 $$ \begin{align*} \Omega_{C_S^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet}:=\frac{\Omega_{C_S^{\dagger}/\mathcal{O}_{\Bbbk}}^{\bullet}}{\displaystyle\bigcap_{i\geq0}\mathfrak{m}_{\Bbbk}^{i+1}\Omega_{C_S^{\dagger}/\mathcal{O}_{\Bbbk}}^{\bullet}} \end{align*} $$
$$ \begin{align*} \Omega_{C_S^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet}:=\frac{\Omega_{C_S^{\dagger}/\mathcal{O}_{\Bbbk}}^{\bullet}}{\displaystyle\bigcap_{i\geq0}\mathfrak{m}_{\Bbbk}^{i+1}\Omega_{C_S^{\dagger}/\mathcal{O}_{\Bbbk}}^{\bullet}} \end{align*} $$
the module of
![]() $\mathfrak {m}_{\Bbbk }$
-separated differentials. Then the above gradings extend to
$\mathfrak {m}_{\Bbbk }$
-separated differentials. Then the above gradings extend to
where d is the de Rham differential. With the valuation conditions on
![]() $\gamma $
and
$\gamma $
and
![]() $\hbar $
for the convergence (see Theorem 4.11), we have the following comparison map.
$\hbar $
for the convergence (see Theorem 4.11), we have the following comparison map.
Theorem 1.1. If
 $\displaystyle \mathrm {val}_p\gamma \leq \frac {1}{p-1}$
and
$\displaystyle \mathrm {val}_p\gamma \leq \frac {1}{p-1}$
and
![]() $\mathrm {val}_p\hbar>0$
, then there is a cochain map
$\mathrm {val}_p\hbar>0$
, then there is a cochain map
defined by the formula
 $$ \begin{align*} \rho_S\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right):=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}} \end{align*} $$
$$ \begin{align*} \rho_S\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right):=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}} \end{align*} $$
together with the
![]() $\Bbbk $
-linearity. Here,
$\Bbbk $
-linearity. Here,
![]() $u,v,\alpha ,\beta $
are multi-indexes with
$u,v,\alpha ,\beta $
are multi-indexes with
 $$ \begin{align} \left\{\begin{array}{@{}ll} \displaystyle x^u:=x_0^{u_0}\cdots x_n^{u_n}, & |u|:=u_0+\cdots+u_n, \\[0.5ex] \displaystyle y^v:=y_1^{v_1}\cdots y_k^{v_k}, & |v|:=v_1+\cdots+v_k, \\[0.5ex] dx_{\alpha}:=dx_{\alpha_1}\wedge\cdots\wedge dx_{\alpha_i}, & |\alpha|:=i \\[0.5ex] dy_{\beta}:=dy_{\beta_1}\wedge\cdots\wedge dy_{\beta_j}, & |\beta|:=j. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{@{}ll} \displaystyle x^u:=x_0^{u_0}\cdots x_n^{u_n}, & |u|:=u_0+\cdots+u_n, \\[0.5ex] \displaystyle y^v:=y_1^{v_1}\cdots y_k^{v_k}, & |v|:=v_1+\cdots+v_k, \\[0.5ex] dx_{\alpha}:=dx_{\alpha_1}\wedge\cdots\wedge dx_{\alpha_i}, & |\alpha|:=i \\[0.5ex] dy_{\beta}:=dy_{\beta_1}\wedge\cdots\wedge dy_{\beta_j}, & |\beta|:=j. \end{array} \right. \end{align} $$
We will see later that the inclusion
is a quasi-isomorphism, and the inclusion
induces a surjection of cohomology spaces with one-dimensional kernel generated by the class
![]() $[dS]$
. By Definition 4.6,
$[dS]$
. By Definition 4.6,
where
![]() $\mathbb {F}_q$
is the residue field of
$\mathbb {F}_q$
is the residue field of
![]() $\mathcal {O}_{\Bbbk }$
, and
$\mathcal {O}_{\Bbbk }$
, and
![]() $\overline {S}=y_1\overline {G}_1+\cdots +y_k\overline {G}_k\in \mathbb {F}_q[x,y]$
is the reduction of S. Since Monsky–Washnitzer cohomology is canonically isomorphic to rigid cohomology for smooth affine schemes, the
$\overline {S}=y_1\overline {G}_1+\cdots +y_k\overline {G}_k\in \mathbb {F}_q[x,y]$
is the reduction of S. Since Monsky–Washnitzer cohomology is canonically isomorphic to rigid cohomology for smooth affine schemes, the
![]() $\rho _S$
in Theorem 1.1 is a comparison map from Dwork cohomology to rigid cohomology.
$\rho _S$
in Theorem 1.1 is a comparison map from Dwork cohomology to rigid cohomology.
On the other hand, if
![]() $X_G\subseteq \mathbb {P}^n_{\Bbbk }$
is the common zero of
$X_G\subseteq \mathbb {P}^n_{\Bbbk }$
is the common zero of
![]() $G_1,\ldots ,G_k$
, then we will see in §2 that there is a canonical map
$G_1,\ldots ,G_k$
, then we will see in §2 that there is a canonical map
inducing a quasi-isomorphism on rigid cohomology spaces. Moreover, by Corollary 4.7, the Monsky–Washnitzer cohomology associated with the bidegree
![]() $(0,0)$
-subalgebra above is computed via the complex of
$(0,0)$
-subalgebra above is computed via the complex of
![]() $\mathfrak {m}_{\Bbbk }$
-adically separated forms of
$\mathfrak {m}_{\Bbbk }$
-adically separated forms of
![]() $C_S^{\dagger }$
. The corresponding statement for algebraic de Rham cohomology is Proposition 2.4. This is a direct generalization of [Reference Monsky26, Th. 9.2] which covers the case of projective hypersurface complement. With the notations so far, we can say more about the comparison map
$C_S^{\dagger }$
. The corresponding statement for algebraic de Rham cohomology is Proposition 2.4. This is a direct generalization of [Reference Monsky26, Th. 9.2] which covers the case of projective hypersurface complement. With the notations so far, we can say more about the comparison map
![]() $\rho _S$
.
$\rho _S$
.
Theorem 1.2.
![]() $\rho _S$
induces an isomorphism
$\rho _S$
induces an isomorphism
for every
![]() $i\geq 2$
. On the other hand,
$i\geq 2$
. On the other hand,
The q-power map induces an endomorphism, called the Frobenius endomorphism on
![]() $\mathbb {F}_q[x,y]$
. This map lifts to endomorphisms
$\mathbb {F}_q[x,y]$
. This map lifts to endomorphisms
both act on the zero forms by sending
![]() $x_i$
and
$x_i$
and
![]() $y_j$
to its qth power
$y_j$
to its qth power
![]() $x_i^q$
and
$x_i^q$
and
![]() $y_j^q$
, respectively. These endomorphisms admit retractions, that is, endomorphisms
$y_j^q$
, respectively. These endomorphisms admit retractions, that is, endomorphisms
such that
![]() $\Psi _{q,S}\circ \Phi _{q,S}$
and
$\Psi _{q,S}\circ \Phi _{q,S}$
and
![]() $\psi \circ \mathrm {Fr}$
are the identity maps, respectively. The detailed expositions will be given in §5. Now, we have the following comparison of the endomorphisms above.
$\psi \circ \mathrm {Fr}$
are the identity maps, respectively. The detailed expositions will be given in §5. Now, we have the following comparison of the endomorphisms above.
Theorem 1.3.
![]() $\rho _S$
is compatible with the Frobenius and the Dwork operators defined on the source and the target, respectively. More precisely, the diagrams
$\rho _S$
is compatible with the Frobenius and the Dwork operators defined on the source and the target, respectively. More precisely, the diagrams


are commutative.
Remark 1.4. In Theorem 1.3, we dropped the subscript
![]() $(\deg _c=0,\deg _w=0)$
in the target of
$(\deg _c=0,\deg _w=0)$
in the target of
![]() $\rho _S$
because we are not sure that an arbitrary lift
$\rho _S$
because we are not sure that an arbitrary lift
![]() $\mathrm {Fr}$
of the q-power map preserves the bidegree
$\mathrm {Fr}$
of the q-power map preserves the bidegree
![]() $(0,0)$
-subcomplex. However, the particular choice such that
$(0,0)$
-subcomplex. However, the particular choice such that
and the
![]() $\psi $
coming from this choice are compatible with the bidegrees so we can recover the subscript
$\psi $
coming from this choice are compatible with the bidegrees so we can recover the subscript
![]() $(\deg _c=0,\deg _w=0)$
in Theorem 1.3. See §§5.1 and 5.2 for the details. We will see in Theorem 4.5 that any lifts of the q-power map define homotopic cochain maps so we can always make such choices.
$(\deg _c=0,\deg _w=0)$
in Theorem 1.3. See §§5.1 and 5.2 for the details. We will see in Theorem 4.5 that any lifts of the q-power map define homotopic cochain maps so we can always make such choices.
We have the following remark concerning formal deformation theory of the Dwork operator, which is not covered in the rest of this article.
Remark 1.5. Using the twisted de Rham complex in Theorem 1.1, we may directly construct a DGBV (differential Gerstenhaber–Batalin–Vilkovisky) algebra with the isomorphic underlying complex, as the authors of [Reference Kim, Kim and Park20] did on the complex geometry setting, and we may develop the formal deformation theory as in [Reference Park and Park31]. Theorem 1.3 enables us to apply this type of formal deformation theory to the Dwork operator. For the detailed discussion in the DGBV aspects of Dwork theory, see [Reference Kim, Park and Park21].
1.3 Outline of the article
In §2, we explain the Cayley trick. In particular, Proposition 2.4 gives a direct sum decomposition of the algebraic de Rham complex of the affine cone and the corresponding decomposition of the algebraic de Rham cohomology. This identification is used in the rest of the article.
In §3, we explicitly write down a comparison map
![]() $\rho _S$
(Definition 3.1) in a corresponding algebraic setting. The comparison for this algebraic
$\rho _S$
(Definition 3.1) in a corresponding algebraic setting. The comparison for this algebraic
![]() $\rho _S$
will be given in Propositions 3.10 and 3.16.
$\rho _S$
will be given in Propositions 3.10 and 3.16.
After establishing the algebraic theory, we will define the required p-adic analytic complexes in §4 and give a proof of Theorems 1.1 and 1.2. In §4.1, we recall the basics on Monsky–Washnitzer cohomology. In particular, Proposition 4.7 is the Monsky–Washnitzer version of Proposition 2.4. This gives the target complex of the
![]() $\rho _S$
in Theorem 1.1. In §4.2, we recall the basics on Dwork complexes and introduce the source complex of the
$\rho _S$
in Theorem 1.1. In §4.2, we recall the basics on Dwork complexes and introduce the source complex of the
![]() $\rho _S$
in Theorem 1.1. Now, the main results of §3 yield Theorem 4.11 which is the combination of Theorems 1.1 and 1.2.
$\rho _S$
in Theorem 1.1. Now, the main results of §3 yield Theorem 4.11 which is the combination of Theorems 1.1 and 1.2.
Finally, in §5, we will prove Theorem 1.3, following Katz’s proof in [Reference Katz19, §III] with some appropriate changes. Namely, Propositions 5.2 and 5.3 together give Theorem 1.3.
The appendix A is an explanation of the computation of algebraic de Rham cohomology via the cosimplicial algebra coming from Čech covering of affine open subsets which is in the proof of Proposition 2.4. Up to the best of author’s knowledge, the suitable reference for this simplest case is not available in the literature so the appendix is added for this article to be more self-contained.
2 The Cayley trick
In this section, we give a detailed explanation of the Cayley trick and its consequences. We begin with motivation. Let
![]() $\Bbbk $
be a field and
$\Bbbk $
be a field and
![]() $X\subseteq \mathbb {P}^n_{\Bbbk }$
a smooth projective complete intersection of codimension k. For a “reasonable” cohomology theory
$X\subseteq \mathbb {P}^n_{\Bbbk }$
a smooth projective complete intersection of codimension k. For a “reasonable” cohomology theory
![]() $H^{\bullet }$
defined for quasiprojective schemes over
$H^{\bullet }$
defined for quasiprojective schemes over
![]() $\Bbbk $
, one may obtain the Gysin exact sequence of the following form:
$\Bbbk $
, one may obtain the Gysin exact sequence of the following form:

The particular cases we consider are:
(1)
![]() $\Bbbk $
is a field of characteristic zero, and
$\Bbbk $
is a field of characteristic zero, and
![]() $H^{\bullet }=H_{\mathrm {dR}}^{\bullet }$
is algebraic de Rham cohomology.
$H^{\bullet }=H_{\mathrm {dR}}^{\bullet }$
is algebraic de Rham cohomology.
(2)
![]() $\Bbbk =\mathbb {F}_q$
is a finite field, and
$\Bbbk =\mathbb {F}_q$
is a finite field, and
![]() $H^{\bullet }=H_{\mathrm {rig}}^{\bullet }$
is rigid cohomology.
$H^{\bullet }=H_{\mathrm {rig}}^{\bullet }$
is rigid cohomology.
Case (2) is mentioned in the introduction (1.1) briefly. For (1), see [Reference Park and Park30, §3.1] for example. In particular, in the cases (1) and (2) above,
by the weak Lefschetz property and Poincaré duality. Denote in this situation
Then
![]() $\mathrm {Res}_X$
induces an isomorphism:
$\mathrm {Res}_X$
induces an isomorphism:
Therefore, we may focus on the cohomology of the complement
![]() $\mathbb {P}^n_{\Bbbk }\setminus X$
. Because we decided to consider the complements, we may assume that
$\mathbb {P}^n_{\Bbbk }\setminus X$
. Because we decided to consider the complements, we may assume that
![]() $X=X_G\subseteq \mathbb {P}^n_{\Bbbk }$
is defined by any finite set of homogeneous polynomials
$X=X_G\subseteq \mathbb {P}^n_{\Bbbk }$
is defined by any finite set of homogeneous polynomials
![]() $G_1,\ldots ,G_k\in \Bbbk [x_0,\ldots ,x_n]$
of positive degrees
$G_1,\ldots ,G_k\in \Bbbk [x_0,\ldots ,x_n]$
of positive degrees
![]() $d_1,\ldots ,d_k$
, respectively. The Cayley trick is a method of translating the computation of
$d_1,\ldots ,d_k$
, respectively. The Cayley trick is a method of translating the computation of
![]() $H^{\bullet }(\mathbb {P}^n_{\Bbbk }\setminus X_G)$
to a computation of the cohomology of the complement of a hypersurface living in a larger space. This larger space is simply given by the projective bundle
$H^{\bullet }(\mathbb {P}^n_{\Bbbk }\setminus X_G)$
to a computation of the cohomology of the complement of a hypersurface living in a larger space. This larger space is simply given by the projective bundle
associated with a locally free
![]() $\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}$
-module
$\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}$
-module
![]() $\mathcal {E}:=\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_1)\oplus \cdots \oplus \mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_k)$
. Another way of describing
$\mathcal {E}:=\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_1)\oplus \cdots \oplus \mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_k)$
. Another way of describing
![]() $\mathbb {P}(\mathcal {E})$
comes from the toric geometry, via the geometric quotient:
$\mathbb {P}(\mathcal {E})$
comes from the toric geometry, via the geometric quotient:
 $$ \begin{align*} \mathbb{P}(\mathcal{E})\cong\frac{(\mathbb{A}^k_{\Bbbk}\setminus0)\times(\mathbb{A}^{n+1}_{\Bbbk}\setminus0)}{\mathbb{G}_m\times\mathbb{G}_m}, \end{align*} $$
$$ \begin{align*} \mathbb{P}(\mathcal{E})\cong\frac{(\mathbb{A}^k_{\Bbbk}\setminus0)\times(\mathbb{A}^{n+1}_{\Bbbk}\setminus0)}{\mathbb{G}_m\times\mathbb{G}_m}, \end{align*} $$
where the
![]() $\mathbb {G}_m\times \mathbb {G}_m$
-action is given by
$\mathbb {G}_m\times \mathbb {G}_m$
-action is given by
Here, the new variables
![]() $y_1,\ldots ,y_k$
correspond to
$y_1,\ldots ,y_k$
correspond to
![]() $\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_1),\ldots ,\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_k)$
, and the action above explains the gradings (1.3). Moreover,
$\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_1),\ldots ,\mathcal {O}_{\mathbb {P}^n_{\Bbbk }}(d_k)$
, and the action above explains the gradings (1.3). Moreover,
![]() $S:=y_1G_1+\cdots +y_kG_k$
being of
$S:=y_1G_1+\cdots +y_kG_k$
being of
![]() $\deg _cS=0$
is equivalent to saying that S is a
$\deg _cS=0$
is equivalent to saying that S is a
![]() $(\mathbb {G}_m\times 1)$
-invariant element. Hence, it defines a hypersurface
$(\mathbb {G}_m\times 1)$
-invariant element. Hence, it defines a hypersurface
![]() $X_S\subseteq \mathbb {P}(\mathcal {E})$
and
$X_S\subseteq \mathbb {P}(\mathcal {E})$
and
so that there is a commutative diagram:

Denote
![]() $X_{G_i}\subseteq \mathbb {P}^n_{\Bbbk }$
the hypersurface cut out by
$X_{G_i}\subseteq \mathbb {P}^n_{\Bbbk }$
the hypersurface cut out by
![]() $G_i$
so
$G_i$
so
![]() $\{\mathbb {P}^n_{\Bbbk }\setminus X_{G_i}\}_{i=1,\ldots ,k}$
is an open covering of
$\{\mathbb {P}^n_{\Bbbk }\setminus X_{G_i}\}_{i=1,\ldots ,k}$
is an open covering of
![]() $\mathbb {P}^n_{\Bbbk }\setminus X_G$
. Since
$\mathbb {P}^n_{\Bbbk }\setminus X_G$
. Since
![]() $\mathcal {E}|_{\mathbb {P}^n_{\Bbbk }\setminus X_{G_i}}\cong \mathcal {O}_{\mathbb {P}^n_{\Bbbk }\setminus X_{G_i}}^{\oplus k-1}$
is a trivial bundle of rank
$\mathcal {E}|_{\mathbb {P}^n_{\Bbbk }\setminus X_{G_i}}\cong \mathcal {O}_{\mathbb {P}^n_{\Bbbk }\setminus X_{G_i}}^{\oplus k-1}$
is a trivial bundle of rank
![]() $k-1$
,
$k-1$
,
![]() $\varphi $
is an
$\varphi $
is an
![]() $\mathbb {A}^{k-1}_{\Bbbk }$
-bundle. In this setting, if an abstract cohomology theory
$\mathbb {A}^{k-1}_{\Bbbk }$
-bundle. In this setting, if an abstract cohomology theory
![]() $H^{\bullet }$
satisfies the Künneth formula, and
$H^{\bullet }$
satisfies the Künneth formula, and
![]() $H^{\bullet }(\mathbb {A}^{k-1}_{\Bbbk })\cong \Bbbk $
, then
$H^{\bullet }(\mathbb {A}^{k-1}_{\Bbbk })\cong \Bbbk $
, then
![]() $\varphi $
induces an isomorphism
$\varphi $
induces an isomorphism
which is true for the cases (1) and (2) above. In this section, we focus on
![]() $H^{\bullet }=H_{\mathrm {dR}}^{\bullet }$
over a characteristic zero field
$H^{\bullet }=H_{\mathrm {dR}}^{\bullet }$
over a characteristic zero field
![]() $\Bbbk $
. Then
$\Bbbk $
. Then
![]() $\varphi $
in (2.3) induces an isomorphism
$\varphi $
in (2.3) induces an isomorphism
Since
![]() $\mathbb {P}(\mathcal {E})\setminus X_S$
is affine with coordinate ring
$\mathbb {P}(\mathcal {E})\setminus X_S$
is affine with coordinate ring
![]() $A:=\Bbbk [x,y,S^{-1}]^{\mathbb {G}_m\times \mathbb {G}_m}$
, we have
$A:=\Bbbk [x,y,S^{-1}]^{\mathbb {G}_m\times \mathbb {G}_m}$
, we have
where
![]() $(\Omega _{A/\Bbbk }^{\bullet },d)$
is the algebraic de Rham complex of A.
$(\Omega _{A/\Bbbk }^{\bullet },d)$
is the algebraic de Rham complex of A.
Notation 2.1. In what follows, we denote
so that
![]() $A\subseteq B\subseteq C_S$
.
$A\subseteq B\subseteq C_S$
.
In the rest of this section, we will describe the algebraic de Rham cohomology of A using the algebraic de Rham cohomology of
![]() $C_S$
. Note that
$C_S$
. Note that
![]() $\operatorname {\mathrm {Spec}} A$
is smooth over
$\operatorname {\mathrm {Spec}} A$
is smooth over
![]() $\Bbbk $
, being an open subset of a smooth
$\Bbbk $
, being an open subset of a smooth
![]() $\Bbbk $
-scheme
$\Bbbk $
-scheme
![]() $\mathbb {P}(\mathcal {E})$
, and
$\mathbb {P}(\mathcal {E})$
, and
![]() $\operatorname {\mathrm {Spec}} B$
is smooth over
$\operatorname {\mathrm {Spec}} B$
is smooth over
![]() $\Bbbk $
, being an open subset of
$\Bbbk $
, being an open subset of
![]() $\mathbb {P}^{k-1}_{\Bbbk }\times \mathbb {A}^{n+1}_{\Bbbk }$
. Since A, B, and
$\mathbb {P}^{k-1}_{\Bbbk }\times \mathbb {A}^{n+1}_{\Bbbk }$
. Since A, B, and
![]() $C_S$
are smooth over
$C_S$
are smooth over
![]() $\Bbbk $
, the inclusions
$\Bbbk $
, the inclusions
![]() $A\subseteq B\subseteq C_S$
induces embeddings
$A\subseteq B\subseteq C_S$
induces embeddings
We will see in Proposition 2.4 that these induce split injections of cohomology spaces. Since the de Rham differential preserves the bidegree
![]() $(\deg _c,\deg _w)$
, the inclusion from
$(\deg _c,\deg _w)$
, the inclusion from
![]() $\Omega _{A/\Bbbk }^{\bullet }$
to
$\Omega _{A/\Bbbk }^{\bullet }$
to
![]() $\Omega _{C_S/\Bbbk }^{\bullet }$
factors through
$\Omega _{C_S/\Bbbk }^{\bullet }$
factors through
where the bidegree
![]() $(0,0)$
part of
$(0,0)$
part of
![]() $\Omega _{C_S/\Bbbk }^{\bullet }$
is the
$\Omega _{C_S/\Bbbk }^{\bullet }$
is the
![]() $\Bbbk $
-linear span of differential forms
$\Bbbk $
-linear span of differential forms
where
![]() $u,v,\alpha ,\beta $
are multi-indexes following convention (1.4) such that
$u,v,\alpha ,\beta $
are multi-indexes following convention (1.4) such that
This explains the gradings (1.3) in the introduction. Then each grading has the corresponding Euler vector field:
 $$ \begin{align*} E_c:=\sum_{i=0}^n\deg_c(x_i)x_i\frac{\partial}{\partial x_i}+\sum_{j=1}^k\deg_c(y_j)y_j\frac{\partial}{\partial y_j}=\sum_{i=0}^nx_i\frac{\partial}{\partial x_i}+\sum_{j=1}^k(-d_jy_j)\frac{\partial}{\partial y_j} \end{align*} $$
$$ \begin{align*} E_c:=\sum_{i=0}^n\deg_c(x_i)x_i\frac{\partial}{\partial x_i}+\sum_{j=1}^k\deg_c(y_j)y_j\frac{\partial}{\partial y_j}=\sum_{i=0}^nx_i\frac{\partial}{\partial x_i}+\sum_{j=1}^k(-d_jy_j)\frac{\partial}{\partial y_j} \end{align*} $$
 $$ \begin{align*} E_w:=\sum_{i=0}^n\deg_w(x_i)x_i\frac{\partial}{\partial x_i}+\sum_{j=1}^k\deg_w(y_j)y_j\frac{\partial}{\partial y_j}=\sum_{j=1}^ky_j\frac{\partial}{\partial y_j}, \end{align*} $$
$$ \begin{align*} E_w:=\sum_{i=0}^n\deg_w(x_i)x_i\frac{\partial}{\partial x_i}+\sum_{j=1}^k\deg_w(y_j)y_j\frac{\partial}{\partial y_j}=\sum_{j=1}^ky_j\frac{\partial}{\partial y_j}, \end{align*} $$
respectively. Denote
the contraction with each Euler vector field.
Lemma 2.2.
![]() $\theta _c$
and
$\theta _c$
and
![]() $\theta _w$
above have the following properties.
$\theta _w$
above have the following properties.
(1)
![]() $\theta _c^2=0$
,
$\theta _c^2=0$
,
![]() $\theta _w^2=0$
, and
$\theta _w^2=0$
, and
![]() $\theta _c\circ \theta _w+\theta _w\circ \theta _c=0$
.
$\theta _c\circ \theta _w+\theta _w\circ \theta _c=0$
.
(2)
![]() $\theta _c$
and
$\theta _c$
and
![]() $\theta _w$
are derivations of the wedge product, that is, if
$\theta _w$
are derivations of the wedge product, that is, if
![]() $\alpha $
is a differential
$\alpha $
is a differential
![]() $\ell $
-form, then
$\ell $
-form, then
(3) For a homogeneous f and
![]() $\lambda \in \Bbbk $
, if we denote
$\lambda \in \Bbbk $
, if we denote
then for a homogeneous
![]() $\xi $
,
$\xi $
,
where the
![]() $\lambda \in \Bbbk $
is regarded as degree zero elements.
$\lambda \in \Bbbk $
is regarded as degree zero elements.
Proof. The results follow from direct computations.
There are several basic but important consequences of Lemma 2.2.
Lemma 2.3. With the notations above, the following hold.
(1) All inclusions in the following commutative square are quasi-isomorphisms:

(2) There are cochain maps induced from
![]() $\theta _c$
and
$\theta _c$
and
![]() $\theta _w$
, respectively:
$\theta _w$
, respectively:
(3) We can identify
and there is a cochain map
Moreover, the following relations hold:
 $$ \begin{align*} \left(\Omega_{B/\Bbbk}^{\bullet},d\right)&=\ker\theta_w\subseteq\left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{\deg_w=0},\\ \left(\Omega_{A/\Bbbk}^{\bullet},d\right)&=\ker\theta_c\subseteq\left(\Omega_{B/\Bbbk}^{\bullet},d\right)_{\deg_c=0}\subseteq\left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{(\deg_c=0,\deg_w=0)}. \end{align*} $$
$$ \begin{align*} \left(\Omega_{B/\Bbbk}^{\bullet},d\right)&=\ker\theta_w\subseteq\left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{\deg_w=0},\\ \left(\Omega_{A/\Bbbk}^{\bullet},d\right)&=\ker\theta_c\subseteq\left(\Omega_{B/\Bbbk}^{\bullet},d\right)_{\deg_c=0}\subseteq\left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{(\deg_c=0,\deg_w=0)}. \end{align*} $$
Proof. From Lemma 2.2(3), we get relations
(1) If
![]() $d\xi =0$
, then
$d\xi =0$
, then
![]() $\xi $
is in the image of d unless
$\xi $
is in the image of d unless
![]() $\left (\deg _c\xi ,\deg _w\xi \right )=(0,0)$
so (1) follows.
$\left (\deg _c\xi ,\deg _w\xi \right )=(0,0)$
so (1) follows.
(2) The above relations also show that each
![]() $\theta $
becomes a cochain map on the subcomplex of homogeneous elements of degree zero.
$\theta $
becomes a cochain map on the subcomplex of homogeneous elements of degree zero.
(3) By Lemma 2.2(1), the image of
![]() $\theta _c\theta _w$
is contained in
$\theta _c\theta _w$
is contained in
![]() $\ker \theta _c\cap \ker \theta _w$
. The asserted identifications follow from general theory of toric varieties (see, e.g., [Reference Batyrev and Cox8, Lem. 8.2]).
$\ker \theta _c\cap \ker \theta _w$
. The asserted identifications follow from general theory of toric varieties (see, e.g., [Reference Batyrev and Cox8, Lem. 8.2]).
Proposition 2.4. With the notations above, there is a decomposition of complexes
 $$ \begin{align*} \left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B/\Bbbk}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B/\Bbbk}^{\bullet},d\right) \end{align*} $$
$$ \begin{align*} \left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B/\Bbbk}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B/\Bbbk}^{\bullet},d\right) \end{align*} $$
and for every
![]() $i\in \mathbb {Z}$
, an isomorphism
$i\in \mathbb {Z}$
, an isomorphism
Consequently, there is an isomorphism for every
![]() $i\in \mathbb {Z}$
:
$i\in \mathbb {Z}$
:
Proof. Each
![]() $\xi \in \Omega _{C_S/\Bbbk }^{\bullet }$
can be decomposed into
$\xi \in \Omega _{C_S/\Bbbk }^{\bullet }$
can be decomposed into
 $$ \begin{align*} \xi=\theta_w\left(\frac{dS}{S}\wedge\xi\right)+\frac{dS}{S}\wedge\theta_w\xi \end{align*} $$
$$ \begin{align*} \xi=\theta_w\left(\frac{dS}{S}\wedge\xi\right)+\frac{dS}{S}\wedge\theta_w\xi \end{align*} $$
so we span
![]() $\Omega _{C_S/\Bbbk }^{\bullet }$
as follows:
$\Omega _{C_S/\Bbbk }^{\bullet }$
as follows:
If
![]() $\xi \in \Omega _{C_S/\Bbbk }^{\bullet }$
is contained in the intersection of summands, that is,
$\xi \in \Omega _{C_S/\Bbbk }^{\bullet }$
is contained in the intersection of summands, that is,
then we may rewrite
![]() $\xi $
as
$\xi $
as
Since
![]() $\theta _w\xi =0$
and
$\theta _w\xi =0$
and
![]() $\theta _w\omega =0$
,
$\theta _w\omega =0$
,
 $$ \begin{align*} \omega=\theta_w\left(\frac{dS}{S}\wedge\omega\right)=\theta_w\xi=0. \end{align*} $$
$$ \begin{align*} \omega=\theta_w\left(\frac{dS}{S}\wedge\omega\right)=\theta_w\xi=0. \end{align*} $$
Therefore, (2.4) becomes a direct sum decomposition:
Since the restriction of
![]() $\theta _w$
on the subspace of
$\theta _w$
on the subspace of
![]() $\deg _w=0$
induces a cochain map by Lemma 2.3, we get a direct sum as a complex:
$\deg _w=0$
induces a cochain map by Lemma 2.3, we get a direct sum as a complex:
 $$ \begin{align} \left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B/\Bbbk}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B/\Bbbk}^{\bullet},d\right). \end{align} $$
$$ \begin{align} \left(\Omega_{C_S/\Bbbk}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B/\Bbbk}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B/\Bbbk}^{\bullet},d\right). \end{align} $$
To compute the direct summand, consider the open subsets for
![]() $j=1,\ldots ,k$
$j=1,\ldots ,k$
where
![]() $X_{y_jG_j}$
is the zero locus of
$X_{y_jG_j}$
is the zero locus of
![]() $y_jG_j$
. These open subsets form an affine open covering of
$y_jG_j$
. These open subsets form an affine open covering of
![]() $\mathbb {P}(\mathcal {E})\setminus X_S$
. On each
$\mathbb {P}(\mathcal {E})\setminus X_S$
. On each
![]() $U_j$
, there is a section of
$U_j$
, there is a section of
![]() $\theta _c$
given by
$\theta _c$
given by

They combine to give a section of the associated Čech–de Rham complex by Proposition A.6 and Example A.7. Since
![]() $\left (\Omega _{A/\Bbbk }^{\bullet },d\right )=\ker \theta _c$
by Lemma 2.3, we obtain
$\left (\Omega _{A/\Bbbk }^{\bullet },d\right )=\ker \theta _c$
by Lemma 2.3, we obtain
Now, the rest part of the proposition follows from combining the two observations so far.
3 Cayley trick and twisted de Rham complexes
In this section, we develop the algebraic de Rham version of Theorems 1.1 and 1.2. This section is a generalization of Monsky’s lecture note [Reference Monsky26, Ch. 9]. We continue with the notation of §2. For fixed
![]() $\hbar ,\gamma \in \Bbbk ^{\times }$
which we regard as formal parameters, consider the twisted de Rham complex over
$\hbar ,\gamma \in \Bbbk ^{\times }$
which we regard as formal parameters, consider the twisted de Rham complex over
![]() $\Bbbk [x,y]$
:
$\Bbbk [x,y]$
:
equipped with the gradings as in (1.3). Then the corresponding comparison map is given as follows.
Definition 3.1. Define the map
by the formula
 $$ \begin{align*} \rho_S\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right):=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}} \end{align*} $$
$$ \begin{align*} \rho_S\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right):=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}} \end{align*} $$
together with the
![]() $\Bbbk $
-linearity.
$\Bbbk $
-linearity.
Under this map, we will obtain comparison results Propositions 3.10 and 3.16. These will be properly completed to give Theorems 1.1 and 1.2. We saw in Lemma 2.3 that the target complex of
![]() $\rho _S$
in Definition 3.1 computes the algebraic de Rham cohomology of
$\rho _S$
in Definition 3.1 computes the algebraic de Rham cohomology of
![]() $C_S=\Bbbk [x,y,S^{-1}]$
. On the other hand, the following lemma explains the effect of taking the subcomplex.
$C_S=\Bbbk [x,y,S^{-1}]$
. On the other hand, the following lemma explains the effect of taking the subcomplex.
Lemma 3.2. The inclusion
is a quasi-isomorphism. On the other hand, the inclusion
induces a surjection on cohomology spaces with one-dimensional kernel spanned by the class of
![]() $dS$
.
$dS$
.
Proof. Since
![]() $\deg _cdS=0$
, the differential
$\deg _cdS=0$
, the differential
![]() $D_{\hbar ,\gamma S}=\hbar d+\hbar d(\gamma S)\wedge -$
is compatible with
$D_{\hbar ,\gamma S}=\hbar d+\hbar d(\gamma S)\wedge -$
is compatible with
![]() $\deg _c$
so the subcomplex is well-defined. Moreover, by Lemma 2.2(3), each
$\deg _c$
so the subcomplex is well-defined. Moreover, by Lemma 2.2(3), each
![]() $\xi \in \Omega _{\Bbbk [x,y]/\Bbbk }^{\bullet }$
homogeneous with respect to
$\xi \in \Omega _{\Bbbk [x,y]/\Bbbk }^{\bullet }$
homogeneous with respect to
![]() $\deg _c$
satisfies the relation
$\deg _c$
satisfies the relation
so if
![]() $D_{\hbar ,\gamma S}\xi =0$
, then
$D_{\hbar ,\gamma S}\xi =0$
, then
![]() $\xi $
is in the image of
$\xi $
is in the image of
![]() $D_{\hbar ,\gamma S}$
unless
$D_{\hbar ,\gamma S}$
unless
![]() $\deg _c\xi =0$
. Hence, the first inclusion is a quasi-isomorphism.
$\deg _c\xi =0$
. Hence, the first inclusion is a quasi-isomorphism.
Note that
![]() $1\in \Omega _{\Bbbk [x,y]/\Bbbk }^{\bullet }$
is the only bidegree
$1\in \Omega _{\Bbbk [x,y]/\Bbbk }^{\bullet }$
is the only bidegree
![]() $(\deg _c,\deg _w)=(0,0)$
element up to scalar multiplication by
$(\deg _c,\deg _w)=(0,0)$
element up to scalar multiplication by
![]() $\Bbbk $
. Since
$\Bbbk $
. Since
![]() $1\in \Omega _{\Bbbk [x,y]/\Bbbk }^{\bullet }$
does not contribute to the cohomology and kills the class
$1\in \Omega _{\Bbbk [x,y]/\Bbbk }^{\bullet }$
does not contribute to the cohomology and kills the class
![]() $[dS]$
. On the other hand, if
$[dS]$
. On the other hand, if
![]() $\deg _wf>0$
, then the equation
$\deg _wf>0$
, then the equation
has no solutions in
![]() $\Bbbk [x,y]$
. Hence,
$\Bbbk [x,y]$
. Hence,
![]() $[dS]$
defines a nontrivial class in the subcomplex with
$[dS]$
defines a nontrivial class in the subcomplex with
![]() $(\deg _c=0,\deg _w>0)$
.
$(\deg _c=0,\deg _w>0)$
.
Remark 3.3. Since
![]() $(-1)!$
is not a well-defined number, in order to extend
$(-1)!$
is not a well-defined number, in order to extend
![]() $\rho _S$
to the
$\rho _S$
to the
![]() $\deg _c=0$
complex, we have to choose the value manually. Since
$\deg _c=0$
complex, we have to choose the value manually. Since
![]() $1$
is the only bidegree
$1$
is the only bidegree
![]() $(\deg _c,\deg _w)=(0,0)$
element up to scalar multiplication by
$(\deg _c,\deg _w)=(0,0)$
element up to scalar multiplication by
![]() $\Bbbk $
, it suffices to consider
$\Bbbk $
, it suffices to consider
![]() $\rho _S(1)$
only. For
$\rho _S(1)$
only. For
![]() $\rho _S$
to be a cochain map,
$\rho _S$
to be a cochain map,
![]() $\rho _S(1)$
must satisfy
$\rho _S(1)$
must satisfy
so
![]() $\rho _S(1)=\log S$
. However, this is impossible in the polynomial ring, and even in the corresponding overconvergent power series ring (Definition 4.1).
$\rho _S(1)=\log S$
. However, this is impossible in the polynomial ring, and even in the corresponding overconvergent power series ring (Definition 4.1).
Notation 3.4. In what follows, we will often denote
as a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\Bbbk $
-vector space so that
$\Bbbk $
-vector space so that
Also, we will often abbreviate the subscripts
to indicate the bidegree restrictions whenever it is clear from the context.
Lemma 3.5. Properties of
![]() $\rho _S$
.
$\rho _S$
.
(1)
![]() $\rho _S$
is a
$\rho _S$
is a
![]() $\Bbbk $
-linear cochain map.
$\Bbbk $
-linear cochain map.
(2)
![]() $\rho _S$
commutes with
$\rho _S$
commutes with
![]() $\theta _c$
and
$\theta _c$
and
![]() $\theta _w$
. Here,
$\theta _w$
. Here,
![]() $\theta _w$
is regarded as a degree
$\theta _w$
is regarded as a degree
![]() $-1$
map of
$-1$
map of
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\Bbbk $
-vector spaces.
$\Bbbk $
-vector spaces.
(3) If
![]() $\xi _1$
and
$\xi _1$
and
![]() $\xi _2$
are
$\xi _2$
are
![]() $\deg _w$
-homogeneous of positive degree, then
$\deg _w$
-homogeneous of positive degree, then
 $$ \begin{align*} \rho_S(\xi_1\wedge\xi_2)=-\frac{(\deg_w\xi_1+\deg_w\xi_2-1)!}{(\deg_w\xi_1-1)!(\deg_w\xi_2-1)!}\rho_S(\xi_1)\wedge\rho_S(\xi_2). \end{align*} $$
$$ \begin{align*} \rho_S(\xi_1\wedge\xi_2)=-\frac{(\deg_w\xi_1+\deg_w\xi_2-1)!}{(\deg_w\xi_1-1)!(\deg_w\xi_2-1)!}\rho_S(\xi_1)\wedge\rho_S(\xi_2). \end{align*} $$
In particular, if
![]() $\xi $
is
$\xi $
is
![]() $\deg _w$
-homogeneous of positive degree, then
$\deg _w$
-homogeneous of positive degree, then
 $$ \begin{align*} \rho_S(\gamma^iS^i\xi)=(-1)^i\frac{(\deg_w\xi+i-1)!}{(\deg_w\xi-1)!}\rho_S(\xi) \end{align*} $$
$$ \begin{align*} \rho_S(\gamma^iS^i\xi)=(-1)^i\frac{(\deg_w\xi+i-1)!}{(\deg_w\xi-1)!}\rho_S(\xi) \end{align*} $$
for every integer
![]() $i>0$
.
$i>0$
.
Proof. The results follow from direct computation.
To describe the kernel of
![]() $\rho _S$
, we introduce the following auxiliary map:
$\rho _S$
, we introduce the following auxiliary map:
Definition 3.6. Define the map
By Lemma 2.2, if
![]() $\xi $
is homogeneous with respect to
$\xi $
is homogeneous with respect to
![]() $\deg _w$
, then
$\deg _w$
, then
Remark 3.7. This map corresponds to the one in [Reference Monsky26, Lem. 9.1] which is defined via the congruence condition on the degree of a defining hypersurface. However, we are working reversely via the Cayley trick. In our context, [Reference Monsky26, Lem. 9.1] becomes Definition 3.6, and Monsky’s definition follows from Lemma 2.2.
Remark 3.8. One may analogously consider
![]() $\epsilon _{c,S}:=D_{\hbar ,\gamma S}\theta _c+\theta _cD_{\hbar ,\gamma S}$
, but this vanishes on the subspace of
$\epsilon _{c,S}:=D_{\hbar ,\gamma S}\theta _c+\theta _cD_{\hbar ,\gamma S}$
, but this vanishes on the subspace of
![]() $\deg _c=0$
by Lemma 2.2.
$\deg _c=0$
by Lemma 2.2.
Lemma 3.9. Properties of
![]() $\epsilon _{w,S}$
.
$\epsilon _{w,S}$
.
(1)
![]() $\epsilon _{w,S}$
is a
$\epsilon _{w,S}$
is a
![]() $\Bbbk $
-linear cochain map.
$\Bbbk $
-linear cochain map.
(2)
![]() $\epsilon _{w,S}$
is injective.
$\epsilon _{w,S}$
is injective.
(3)
![]() $\epsilon _{w,S}$
restricts to the bidegree
$\epsilon _{w,S}$
restricts to the bidegree
![]() $(\deg _c=0,\deg _w>0)$
-subcomplex:
$(\deg _c=0,\deg _w>0)$
-subcomplex:
If
![]() $\xi \in \mathscr {L}_{(0,+)}^{\bullet }$
is a
$\xi \in \mathscr {L}_{(0,+)}^{\bullet }$
is a
![]() $\deg _w$
-homogeneous element, then
$\deg _w$
-homogeneous element, then
 $$ \begin{align*} \gamma^iS^i\xi\equiv(-1)^i\frac{(\deg_w\xi+i-1)!}{(\deg_w\xi-1)!}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}. \end{align*} $$
$$ \begin{align*} \gamma^iS^i\xi\equiv(-1)^i\frac{(\deg_w\xi+i-1)!}{(\deg_w\xi-1)!}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}. \end{align*} $$
Proof. (1)
![]() $\epsilon _{w,S}$
is
$\epsilon _{w,S}$
is
![]() $\Bbbk $
-linear by construction and is a cochain map by
$\Bbbk $
-linear by construction and is a cochain map by
(2) If
![]() $\xi $
is a nonzero
$\xi $
is a nonzero
![]() $\deg _w$
-homogeneous element, then
$\deg _w$
-homogeneous element, then
is nonzero by our choice of S.
(3) We proceed by induction on the power i. The case
![]() $i=1$
follows immediately from construction. If
$i=1$
follows immediately from construction. If
![]() $i>1$
, then
$i>1$
, then
 $$ \begin{align*} (\gamma S)^i\xi&=(\gamma S)(\gamma S)^{i-1}\xi\\ &\equiv-(\deg_w\xi+i-1)(\gamma S)^{i-1}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}\\ &\equiv-(\deg_w\xi+i-1)\cdot(-1)^{i-1}\frac{(\deg_w\xi+i-2)!}{(\deg_w\xi-1)!}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}\\ &\equiv(-1)^i\frac{(\deg_w\xi+i-1)!}{(\deg_w\xi-1)!}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}, \end{align*} $$
$$ \begin{align*} (\gamma S)^i\xi&=(\gamma S)(\gamma S)^{i-1}\xi\\ &\equiv-(\deg_w\xi+i-1)(\gamma S)^{i-1}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}\\ &\equiv-(\deg_w\xi+i-1)\cdot(-1)^{i-1}\frac{(\deg_w\xi+i-2)!}{(\deg_w\xi-1)!}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}\\ &\equiv(-1)^i\frac{(\deg_w\xi+i-1)!}{(\deg_w\xi-1)!}\xi\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}, \end{align*} $$
where the third line follows from induction hypothesis.
Proposition 3.10. With notation 3.4, there is an exact sequence of cochain complexes
Consequently, there is an exact sequence
for every
![]() $i\in \mathbb {Z}$
, and in particular,
$i\in \mathbb {Z}$
, and in particular,
Proof. Since the target of
![]() $\rho _S$
admits a
$\rho _S$
admits a
![]() $\Bbbk $
-basis
$\Bbbk $
-basis
 $$ \begin{align*} \left\{\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\ \middle|\ |u|+|\alpha|=v_1d_1+\cdots+v_kd_k+d_{\beta_1}+\cdots+d_{\beta_{|\beta|}}\right\} \end{align*} $$
$$ \begin{align*} \left\{\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\ \middle|\ |u|+|\alpha|=v_1d_1+\cdots+v_kd_k+d_{\beta_1}+\cdots+d_{\beta_{|\beta|}}\right\} \end{align*} $$
which is in the image of
![]() $\rho _S$
, the surjectivity of
$\rho _S$
, the surjectivity of
![]() $\rho _S$
follows. The injectivity of
$\rho _S$
follows. The injectivity of
![]() $\epsilon _{w,S}$
follows from Lemma 3.9. If
$\epsilon _{w,S}$
follows from Lemma 3.9. If
![]() $\xi \in \mathscr {L}_{(0,+)}^{\bullet }$
is
$\xi \in \mathscr {L}_{(0,+)}^{\bullet }$
is
![]() $\deg _w$
-homogeneous, then
$\deg _w$
-homogeneous, then
by Lemma 3.5. Hence,
![]() $\rho _S$
induces
$\rho _S$
induces

Define the map of graded
![]() $\Bbbk $
-vector spaces
$\Bbbk $
-vector spaces

by the formula
 $$ \begin{align*} \sigma\left(\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\right):=(-1)^{|v|+|\beta|-1}\frac{\hbar^{|\alpha|+|\beta|}\gamma^{|v|+|\beta|}}{(|v|+|\beta|-1)!}x^uy^vdx_{\alpha}\wedge dy_{\beta} \end{align*} $$
$$ \begin{align*} \sigma\left(\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\right):=(-1)^{|v|+|\beta|-1}\frac{\hbar^{|\alpha|+|\beta|}\gamma^{|v|+|\beta|}}{(|v|+|\beta|-1)!}x^uy^vdx_{\alpha}\wedge dy_{\beta} \end{align*} $$
for
![]() $|v|+|\beta |>0$
together with the
$|v|+|\beta |>0$
together with the
![]() $\Bbbk $
-linearity. From
$\Bbbk $
-linearity. From
 $$ \begin{align*} &\quad\sigma\left(\frac{S^i}{S^i}\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\right)\\ &=(-1)^{|v|+|\beta|+i-1}\frac{\hbar^{|\alpha|+|\beta|}\gamma^{|v|+|\beta|+i}}{(|v|+|\beta|+i-1)!}S^ix^uy^vdx_{\alpha}\wedge dy_{\beta}\\ &\equiv(-1)^{|v|+|\beta|-1}\frac{\hbar^{|\alpha|+|\beta|}\gamma^{|v|+|\beta|}}{(|v|+|\beta|-1)!}x^uy^vdx_{\alpha}\wedge dy_{\beta}\quad\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}\\ &=\sigma\left(\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\right), \end{align*} $$
$$ \begin{align*} &\quad\sigma\left(\frac{S^i}{S^i}\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\right)\\ &=(-1)^{|v|+|\beta|+i-1}\frac{\hbar^{|\alpha|+|\beta|}\gamma^{|v|+|\beta|+i}}{(|v|+|\beta|+i-1)!}S^ix^uy^vdx_{\alpha}\wedge dy_{\beta}\\ &\equiv(-1)^{|v|+|\beta|-1}\frac{\hbar^{|\alpha|+|\beta|}\gamma^{|v|+|\beta|}}{(|v|+|\beta|-1)!}x^uy^vdx_{\alpha}\wedge dy_{\beta}\quad\mod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet}\\ &=\sigma\left(\frac{x^uy^v}{S^{|v|}}dx_{\alpha}\wedge\frac{dy_{\beta}}{S^{|\beta|}}\right), \end{align*} $$
we see that
![]() $\sigma $
is well-defined. Note that this forces
$\sigma $
is well-defined. Note that this forces
![]() $\sigma (1)=\gamma S$
. By construction,
$\sigma (1)=\gamma S$
. By construction,
![]() $\overline {\rho }_S\sigma $
is the identity. Since
$\overline {\rho }_S\sigma $
is the identity. Since
![]() $\operatorname {\mathrm {coker}}\epsilon _{w,S}$
is spanned over
$\operatorname {\mathrm {coker}}\epsilon _{w,S}$
is spanned over
![]() $\Bbbk $
by
$\Bbbk $
by
![]() $S^ix^uy^vdx_{\alpha }\wedge dy_{\beta }$
with
$S^ix^uy^vdx_{\alpha }\wedge dy_{\beta }$
with
![]() $i\geq 0$
and
$i\geq 0$
and
![]() $|v|+|\beta |>0$
, and
$|v|+|\beta |>0$
, and
 $$ \begin{align*} \gamma^iS^ix^uy^vdx_{\alpha}\wedge dy_{\beta}\equiv(-1)^i\frac{(|v|+|\beta|+i-1)!}{(|v|+|\beta|-1)!}x^uy^vdx_{\alpha}\wedge dy_{\beta}\bmod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet} \end{align*} $$
$$ \begin{align*} \gamma^iS^ix^uy^vdx_{\alpha}\wedge dy_{\beta}\equiv(-1)^i\frac{(|v|+|\beta|+i-1)!}{(|v|+|\beta|-1)!}x^uy^vdx_{\alpha}\wedge dy_{\beta}\bmod\epsilon_{w,S}\mathscr{L}_{(0,+)}^{\bullet} \end{align*} $$
is in the image of
![]() $\sigma $
, we conclude that
$\sigma $
, we conclude that
![]() $\sigma $
is surjective. Hence,
$\sigma $
is surjective. Hence,
![]() $\overline {\rho }_S$
and
$\overline {\rho }_S$
and
![]() $\sigma $
are mutually inverses. Therefore, we achieve the desired exactness.
$\sigma $
are mutually inverses. Therefore, we achieve the desired exactness.
For the second part, take the cohomology long exact sequence. Since
![]() $\epsilon _{w,S}$
is homotopic to zero by definition of
$\epsilon _{w,S}$
is homotopic to zero by definition of
![]() $\epsilon _{w,S}$
and Lemma 3.9, we get the desired exact sequences. In particular, the long exact sequence begins with
$\epsilon _{w,S}$
and Lemma 3.9, we get the desired exact sequences. In particular, the long exact sequence begins with

Hence, we get the desired vanishing and the
![]() $\delta $
becomes an isomorphism
$\delta $
becomes an isomorphism
Since
![]() $\operatorname {\mathrm {Spec}} C_S=\operatorname {\mathrm {Spec}}\Bbbk [x,y,S^{-1}]$
is connected, the right-hand side is one-dimensional with a basis
$\operatorname {\mathrm {Spec}} C_S=\operatorname {\mathrm {Spec}}\Bbbk [x,y,S^{-1}]$
is connected, the right-hand side is one-dimensional with a basis
![]() $[dS]$
coming from 3.2.
$[dS]$
coming from 3.2.
Corollary 3.11. The cohomology groups of the twisted de Rham complex
are finite-dimensional
![]() $\Bbbk $
-vector spaces for every
$\Bbbk $
-vector spaces for every
![]() $i\in \mathbb {Z}$
. In particular,
$i\in \mathbb {Z}$
. In particular,
Proof. By Lemma 3.2, we may compute the cohomology of the twisted de Rham complex by using
![]() $\left (\mathscr {L}_{(0,+)}^{\bullet },D_{\hbar ,\gamma S}\right )$
. Hence, the results follow from Proposition 3.10 and the finiteness of the algebraic de Rham cohomology of smooth
$\left (\mathscr {L}_{(0,+)}^{\bullet },D_{\hbar ,\gamma S}\right )$
. Hence, the results follow from Proposition 3.10 and the finiteness of the algebraic de Rham cohomology of smooth
![]() $\Bbbk $
-algebras [Reference Monsky28, Th. 3.1].
$\Bbbk $
-algebras [Reference Monsky28, Th. 3.1].
To describe the image of
![]() $\rho _S$
on the cohomology spaces, we introduce the following auxiliary map.
$\rho _S$
on the cohomology spaces, we introduce the following auxiliary map.
Definition 3.12. Define the
![]() $\Bbbk $
-linear map
$\Bbbk $
-linear map
as follows: If
![]() $\xi $
is a
$\xi $
is a
![]() $\deg _w\xi $
-homogeneous of positive degree, then denote
$\deg _w\xi $
-homogeneous of positive degree, then denote
 $$ \begin{align*} \chi_{\xi}:=\left\{\begin{array}{ll} 0, & \textrm{if}\quad\deg_w\xi=1,\\ \displaystyle-\left(1+\frac{1}{2}+\cdots+\frac{1}{\deg_w\xi-1}\right), & \textrm{if}\quad\deg_w\xi>1, \end{array} \right. \end{align*} $$
$$ \begin{align*} \chi_{\xi}:=\left\{\begin{array}{ll} 0, & \textrm{if}\quad\deg_w\xi=1,\\ \displaystyle-\left(1+\frac{1}{2}+\cdots+\frac{1}{\deg_w\xi-1}\right), & \textrm{if}\quad\deg_w\xi>1, \end{array} \right. \end{align*} $$
and define
![]() $\chi (\xi ):=\chi _{\xi }\cdot \xi $
on
$\chi (\xi ):=\chi _{\xi }\cdot \xi $
on
![]() $\deg _w\xi $
-homogeneous elements.
$\deg _w\xi $
-homogeneous elements.
Remark 3.13. This map corresponds to the one in [Reference Monsky26, p. 110]. The additional grading
![]() $\deg _w$
coming from the Cayley trick replaces the role of the congruence condition on the degree of a defining hypersurface in Monsky’s definition.
$\deg _w$
coming from the Cayley trick replaces the role of the congruence condition on the degree of a defining hypersurface in Monsky’s definition.
Lemma 3.14. As a cochain map, the following hold.
Proof. If
![]() $\xi $
is a
$\xi $
is a
![]() $\deg _w$
-homogeneous element, then
$\deg _w$
-homogeneous element, then
 $$ \begin{align*} (\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi)(\xi)&=\chi_{\xi}\hbar d\xi+\chi_{dS\wedge\xi}\hbar\gamma dS\wedge\xi-\chi_{\xi}\hbar d\xi-\chi_{\xi}\hbar\gamma dS\wedge\xi\\ &=-\frac{\hbar\gamma}{\deg_w\xi}dS\wedge\xi \end{align*} $$
$$ \begin{align*} (\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi)(\xi)&=\chi_{\xi}\hbar d\xi+\chi_{dS\wedge\xi}\hbar\gamma dS\wedge\xi-\chi_{\xi}\hbar d\xi-\chi_{\xi}\hbar\gamma dS\wedge\xi\\ &=-\frac{\hbar\gamma}{\deg_w\xi}dS\wedge\xi \end{align*} $$
because
![]() $\deg _w(dS\wedge \xi )=\deg _w\xi +1$
. By Lemma 3.5, this gives
$\deg _w(dS\wedge \xi )=\deg _w\xi +1$
. By Lemma 3.5, this gives
 $$ \begin{align*} (\rho_S\circ(\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi))(\xi)&=-\frac{\hbar\gamma}{\deg_w\xi}\rho_S(dS\wedge\xi)\\ &=\frac{\hbar\gamma}{\deg_w\xi}\frac{(\deg_w\xi)!}{(\deg_w\xi-1)!}\rho_S(dS)\wedge\rho_S(\xi)\\ &=\frac{dS}{S}\wedge\rho_S(\xi) \end{align*} $$
$$ \begin{align*} (\rho_S\circ(\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi))(\xi)&=-\frac{\hbar\gamma}{\deg_w\xi}\rho_S(dS\wedge\xi)\\ &=\frac{\hbar\gamma}{\deg_w\xi}\frac{(\deg_w\xi)!}{(\deg_w\xi-1)!}\rho_S(dS)\wedge\rho_S(\xi)\\ &=\frac{dS}{S}\wedge\rho_S(\xi) \end{align*} $$
so the lemma follows.
Lemma 3.15. With Notations 2.1 and 3.4, the square

commutes up to homotopy where we use the identification coming from the decomposition in Proposition 2.4.
Proof. Using Lemmas 3.5, 3.9, and 3.14, and Proposition 3.10, we get
 $$ \begin{align*} d\rho_S\theta_w\chi+\rho_S\theta_w\chi D_{\hbar,\gamma S}&=\rho_SD_{\hbar,\gamma S}\theta_w\chi+\rho_S\theta_w\chi D_{\hbar,\gamma S}\\ &=\rho_S(D_{\hbar,\gamma S}\theta_w+\theta_wD_{\hbar,\gamma S})\chi+\rho_S\theta(\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi)\\ &=\rho_S\epsilon_{w,S}\chi+\theta_w\rho_S(\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi)\\ &=\theta_w\left(\frac{dS}{S}\wedge\rho_S\right)\\ &=\rho_S-\frac{dS}{S}\wedge\theta_w\rho_S, \end{align*} $$
$$ \begin{align*} d\rho_S\theta_w\chi+\rho_S\theta_w\chi D_{\hbar,\gamma S}&=\rho_SD_{\hbar,\gamma S}\theta_w\chi+\rho_S\theta_w\chi D_{\hbar,\gamma S}\\ &=\rho_S(D_{\hbar,\gamma S}\theta_w+\theta_wD_{\hbar,\gamma S})\chi+\rho_S\theta(\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi)\\ &=\rho_S\epsilon_{w,S}\chi+\theta_w\rho_S(\chi D_{\hbar,\gamma S}-D_{\hbar,\gamma S}\chi)\\ &=\theta_w\left(\frac{dS}{S}\wedge\rho_S\right)\\ &=\rho_S-\frac{dS}{S}\wedge\theta_w\rho_S, \end{align*} $$
where
![]() $\theta _w\rho _S$
maps into
$\theta _w\rho _S$
maps into
![]() $\Omega _{B/\Bbbk }^{\bullet }$
by Lemma 2.3.
$\Omega _{B/\Bbbk }^{\bullet }$
by Lemma 2.3.
Proposition 3.16. In the exact sequence as in Proposition 3.10 for
![]() $i\in \mathbb {Z}$
:
$i\in \mathbb {Z}$
:
![]() $\rho _S$
and
$\rho _S$
and
![]() $\delta $
above induce isomorphisms
$\delta $
above induce isomorphisms
Here, we use the identification of Proposition 2.4. Consequently,
![]() $\rho _S$
induces
$\rho _S$
induces
for every
![]() $i\geq 2$
.
$i\geq 2$
.
Proof. Suppose that
![]() $\xi \in \Omega _{\Bbbk [x,y]/\Bbbk }^{i+1}$
is a
$\xi \in \Omega _{\Bbbk [x,y]/\Bbbk }^{i+1}$
is a
![]() $D_{\hbar ,\gamma S}$
-closed form. If we take
$D_{\hbar ,\gamma S}$
-closed form. If we take
then
![]() $\omega \in \Omega _{B/\Bbbk }^i$
and
$\omega \in \Omega _{B/\Bbbk }^i$
and
Since
![]() $\omega $
is in the image of
$\omega $
is in the image of
![]() $\rho _S$
, it represents a class in
$\rho _S$
, it represents a class in
![]() $H^i(\Omega _{B/\Bbbk }^{\bullet },d)$
. Now,
$H^i(\Omega _{B/\Bbbk }^{\bullet },d)$
. Now,
![]() $\theta _w\xi $
is a lift of
$\theta _w\xi $
is a lift of
![]() $\omega $
along
$\omega $
along
![]() $\rho _S$
and, since
$\rho _S$
and, since
![]() $D_{\hbar ,\gamma S}\xi =0$
, we have
$D_{\hbar ,\gamma S}\xi =0$
, we have
Therefore, by the construction of connecting map
![]() $\delta $
,
$\delta $
,
so
![]() $\delta $
restricted to
$\delta $
restricted to
![]() $H^i(\Omega _{B/\Bbbk }^{\bullet },d)$
is surjective.
$H^i(\Omega _{B/\Bbbk }^{\bullet },d)$
is surjective.
On the other hand,
![]() $\rho _S$
defines an injection into
$\rho _S$
defines an injection into
![]() $H^{i-1}(\Omega _{B/\Bbbk }^{\bullet },d)$
by Proposition 3.10 and Lemma 3.15. If
$H^{i-1}(\Omega _{B/\Bbbk }^{\bullet },d)$
by Proposition 3.10 and Lemma 3.15. If
![]() $\xi \in H^{i-1}(\Omega _{B/\Bbbk }^{\bullet },d)$
, then there is
$\xi \in H^{i-1}(\Omega _{B/\Bbbk }^{\bullet },d)$
, then there is
![]() $\widetilde {\xi }\in H^i(\Omega _{B/\Bbbk }^{\bullet },d)$
with
$\widetilde {\xi }\in H^i(\Omega _{B/\Bbbk }^{\bullet },d)$
with
 $$ \begin{align*} \delta\widetilde{\xi}=\delta\left(\frac{dS}{S}\wedge\xi\right) \end{align*} $$
$$ \begin{align*} \delta\widetilde{\xi}=\delta\left(\frac{dS}{S}\wedge\xi\right) \end{align*} $$
by the surjectivity of
![]() $\delta $
observed above. Hence,
$\delta $
observed above. Hence,
but this implies
![]() $\widetilde {\xi }=0$
by Lemma 3.15. Hence,
$\widetilde {\xi }=0$
by Lemma 3.15. Hence,
![]() $\rho _S$
is surjective as well, that is, it is an isomorphism. By the identification of Proposition 2.4, this implies that
$\rho _S$
is surjective as well, that is, it is an isomorphism. By the identification of Proposition 2.4, this implies that
![]() $\delta $
is an isomorphism as well. The last assertion follows from Proposition 2.4 together with Lemma 3.2.
$\delta $
is an isomorphism as well. The last assertion follows from Proposition 2.4 together with Lemma 3.2.
4 p-adic cohomology and Cayley trick
In this section, we will prove Theorems 1.1 and 1.2, by constructing p-adic models of the complexes studied in §2 and §3, respectively. From now on,
![]() $\Bbbk $
will be a finite extension of
$\Bbbk $
will be a finite extension of
![]() $\mathbb {Q}_p$
with the valuation ring
$\mathbb {Q}_p$
with the valuation ring
![]() $(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })$
and the residue field
$(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })$
and the residue field
![]() $\mathbb {F}_q$
. Also, we keep the notation in §2 and §3, but we assume that
$\mathbb {F}_q$
. Also, we keep the notation in §2 and §3, but we assume that
![]() $G_1,\ldots ,G_k$
belong to
$G_1,\ldots ,G_k$
belong to
![]() $\mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
and their reductions
$\mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
and their reductions
![]() $\overline {G}_1,\ldots ,\overline {G}_k$
are nonzero in
$\overline {G}_1,\ldots ,\overline {G}_k$
are nonzero in
![]() $\mathbb {F}_q[x_0,\ldots ,x_n]$
.
$\mathbb {F}_q[x_0,\ldots ,x_n]$
.
4.1 Monsky–Washnitzer cohomology
In this subsection, we briefly review the theory of Monsky–Washnitzer cohomology, which gives a p-adic model of algebraic de Rham cohomology studied in §2. Using this, we translate Proposition 2.4 into Monsky–Washnitzer setting and get the corresponding results in Proposition 4.7.
Definition 4.1. Denote the ring of overconvergent power series over
![]() $\mathcal {O}_{\Bbbk }$
by
$\mathcal {O}_{\Bbbk }$
by
 $$ \begin{align*} \mathcal{O}_{\Bbbk}\{t_1,\ldots,t_n\}^{\dagger}=\left\{\sum_{u\in\mathbb{Z}_{\geq0}^{\oplus n}}c_ut^u\in\mathcal{O}_{\Bbbk}[[t_1,\ldots,t_n]]\ \middle|\ \begin{array}{c} \textrm{there is } r>1 \textrm{ such that} \\ \displaystyle\lim_{|u|\rightarrow\infty}c_ur^u=0 \end{array}\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\Bbbk}\{t_1,\ldots,t_n\}^{\dagger}=\left\{\sum_{u\in\mathbb{Z}_{\geq0}^{\oplus n}}c_ut^u\in\mathcal{O}_{\Bbbk}[[t_1,\ldots,t_n]]\ \middle|\ \begin{array}{c} \textrm{there is } r>1 \textrm{ such that} \\ \displaystyle\lim_{|u|\rightarrow\infty}c_ur^u=0 \end{array}\right\}. \end{align*} $$
Then a weakly complete finitely generated algebra over
![]() $\mathcal {O}_{\Bbbk }$
is a homomorphic image of some overconvergent power series ring.
$\mathcal {O}_{\Bbbk }$
is a homomorphic image of some overconvergent power series ring.
Proposition 4.2.
![]() $\mathcal {O}_{\Bbbk }\{t_1,\ldots ,t_m\}^{\dagger }$
satisfies Weierstrass’ preparation and division. Consequently,
$\mathcal {O}_{\Bbbk }\{t_1,\ldots ,t_m\}^{\dagger }$
satisfies Weierstrass’ preparation and division. Consequently,
(1)
![]() $\mathcal {O}_{\Bbbk }\{t_1,\ldots ,t_n\}^{\dagger }$
is Noetherian, and
$\mathcal {O}_{\Bbbk }\{t_1,\ldots ,t_n\}^{\dagger }$
is Noetherian, and
(2) the inclusion
![]() $\mathcal {O}_{\Bbbk }[t_1,\ldots ,t_n]\subseteq \mathcal {O}_{\Bbbk }\{t_1,\ldots ,t_n\}^{\dagger }$
is flat.
$\mathcal {O}_{\Bbbk }[t_1,\ldots ,t_n]\subseteq \mathcal {O}_{\Bbbk }\{t_1,\ldots ,t_n\}^{\dagger }$
is flat.
Proof. This is [Reference Van der Put32, Prop. 2.2].
Definition 4.3. Given an
![]() $\mathcal {O}_{\Bbbk }$
-algebra A, denote
$\mathcal {O}_{\Bbbk }$
-algebra A, denote

which is called the
![]() $\mathfrak {m}_{\Bbbk }$
-separated (or
$\mathfrak {m}_{\Bbbk }$
-separated (or
![]() $\mathfrak {m}_{\Bbbk }$
-continuous) differentials on A.
$\mathfrak {m}_{\Bbbk }$
-continuous) differentials on A.
Definition 4.4. Given an (usually smooth)
![]() $\mathbb {F}_q$
-algebra
$\mathbb {F}_q$
-algebra
![]() $\overline {A}$
, a w.c.f.g.
$\overline {A}$
, a w.c.f.g.
![]() $\mathcal {O}_{\Bbbk }$
-algebra A is called a lift if A is flat over
$\mathcal {O}_{\Bbbk }$
-algebra A is called a lift if A is flat over
![]() $\mathcal {O}_{\Bbbk }$
and
$\mathcal {O}_{\Bbbk }$
and
![]() $A/\mathfrak {m}_{\Bbbk } A\cong \overline {A}$
.
$A/\mathfrak {m}_{\Bbbk } A\cong \overline {A}$
.
Theorem 4.5. Given a smooth
![]() $\mathbb {F}_q$
-algebra
$\mathbb {F}_q$
-algebra
![]() $\overline {A}$
, there is always a lift A of
$\overline {A}$
, there is always a lift A of
![]() $\overline {A}$
. Moreover, the following hold.
$\overline {A}$
. Moreover, the following hold.
(1) Every lift of
![]() $\overline {A}$
is isomorphic to A as an
$\overline {A}$
is isomorphic to A as an
![]() $\mathcal {O}_{\Bbbk }$
-algebra.
$\mathcal {O}_{\Bbbk }$
-algebra.
(2) Let
![]() $\overline {B}$
be a smooth
$\overline {B}$
be a smooth
![]() $\mathbb {F}_q$
-algebra with a lift B. If
$\mathbb {F}_q$
-algebra with a lift B. If
![]() $\overline {\varphi }:\overline {A}\rightarrow \overline {B}$
is an
$\overline {\varphi }:\overline {A}\rightarrow \overline {B}$
is an
![]() $\mathbb {F}_q$
-algebra map, then there is an
$\mathbb {F}_q$
-algebra map, then there is an
![]() $\mathcal {O}_{\Bbbk }$
-algebra map
$\mathcal {O}_{\Bbbk }$
-algebra map
![]() $\varphi :A\rightarrow B$
such that
$\varphi :A\rightarrow B$
such that
(3) If
![]() $\varphi ,\psi :A\rightarrow C$
are two maps into a w.c.f.g.
$\varphi ,\psi :A\rightarrow C$
are two maps into a w.c.f.g.
![]() $\mathcal {O}_{\Bbbk }$
-algebra such that
$\mathcal {O}_{\Bbbk }$
-algebra such that
then the induced maps
are homotopic.
Proof. This is [Reference Van der Put32, Th. 2.4.4].
Definition 4.6. Let
![]() $\overline {A}$
be a smooth
$\overline {A}$
be a smooth
![]() $\mathbb {F}_q$
-algebra. Define
$\mathbb {F}_q$
-algebra. Define
where A is any lift of
![]() $\overline {A}$
given by Theorem 4.5.
$\overline {A}$
given by Theorem 4.5.
Return to the situation of §2, but with the assumption that
![]() $G_1,\ldots ,G_k$
belong to
$G_1,\ldots ,G_k$
belong to
![]() $\mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
and their reductions
$\mathcal {O}_{\Bbbk }[x_0,\ldots ,x_n]$
and their reductions
![]() $\overline {G}_1,\ldots ,\overline {G}_k$
in
$\overline {G}_1,\ldots ,\overline {G}_k$
in
![]() $\mathbb {F}_q[x_0,\ldots ,x_n]$
are nonzero. As we observed in §2, there is an isomorphism
$\mathbb {F}_q[x_0,\ldots ,x_n]$
are nonzero. As we observed in §2, there is an isomorphism
coming from (2.3). Following Notations 2.1 and 3.4, we denote
Then the w.c.f.g.
![]() $\mathcal {O}_{\Bbbk }$
-algebra
$\mathcal {O}_{\Bbbk }$
-algebra
 $$ \begin{align*} C_S^{\dagger}=\mathcal{O}_{\Bbbk}\{x,y,S^{-1}\}^{\dagger}\cong\frac{\mathcal{O}_{\Bbbk}\{x,y,t\}^{\dagger}}{(tS-1)} \end{align*} $$
$$ \begin{align*} C_S^{\dagger}=\mathcal{O}_{\Bbbk}\{x,y,S^{-1}\}^{\dagger}\cong\frac{\mathcal{O}_{\Bbbk}\{x,y,t\}^{\dagger}}{(tS-1)} \end{align*} $$
satisfies
 $$ \begin{align*} \frac{C_S^{\dagger}}{\mathfrak{m}_{\Bbbk} C_S^{\dagger}}\cong\frac{\mathbb{F}_q[x,y,t]}{(t\overline{S}-1)}\cong\mathbb{F}_q[x,y,\overline{S}^{-1}]. \end{align*} $$
$$ \begin{align*} \frac{C_S^{\dagger}}{\mathfrak{m}_{\Bbbk} C_S^{\dagger}}\cong\frac{\mathbb{F}_q[x,y,t]}{(t\overline{S}-1)}\cong\mathbb{F}_q[x,y,\overline{S}^{-1}]. \end{align*} $$
Moreover, its subalgebras
are still w.c.f.g.
![]() $\mathcal {O}_{\Bbbk }$
-algebras such that
$\mathcal {O}_{\Bbbk }$
-algebras such that
 $$ \begin{align*} \frac{A^{\dagger}}{\mathfrak{m}_{\Bbbk} A^{\dagger}}\cong\mathbb{F}_q[x,y,\overline{S}^{-1}]_{(0,0)}\cong\overline{\mathcal{O}}_A,\quad\frac{B^{\dagger}}{\mathfrak{m}_{\Bbbk} B^{\dagger}}\cong\mathbb{F}_q[x,y,\overline{S}^{-1}]_{\deg_w=0}\cong\overline{\mathcal{O}}_B. \end{align*} $$
$$ \begin{align*} \frac{A^{\dagger}}{\mathfrak{m}_{\Bbbk} A^{\dagger}}\cong\mathbb{F}_q[x,y,\overline{S}^{-1}]_{(0,0)}\cong\overline{\mathcal{O}}_A,\quad\frac{B^{\dagger}}{\mathfrak{m}_{\Bbbk} B^{\dagger}}\cong\mathbb{F}_q[x,y,\overline{S}^{-1}]_{\deg_w=0}\cong\overline{\mathcal{O}}_B. \end{align*} $$
Hence,
![]() $A^{\dagger }$
,
$A^{\dagger }$
,
![]() $B^{\dagger }$
, and
$B^{\dagger }$
, and
![]() $C_S^{\dagger }$
compute the Monsky–Washnitzer of
$C_S^{\dagger }$
compute the Monsky–Washnitzer of
![]() $\overline {\mathcal {O}}_A$
,
$\overline {\mathcal {O}}_A$
,
![]() $\overline {\mathcal {O}}_B$
, and
$\overline {\mathcal {O}}_B$
, and
![]() $\overline {\mathcal {O}}_{C_S}$
, respectively: for
$\overline {\mathcal {O}}_{C_S}$
, respectively: for
![]() $R=A$
, B, or
$R=A$
, B, or
![]() $C_S$
,
$C_S$
,
Proposition 4.7. With the notations above, there is a decomposition of complexes
 $$ \begin{align*} \left(\Omega_{C_S^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right) \end{align*} $$
$$ \begin{align*} \left(\Omega_{C_S^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right) \end{align*} $$
and for every
![]() $i\in \mathbb {Z}$
, an isomorphism
$i\in \mathbb {Z}$
, an isomorphism
Consequently, there is an isomorphism for every
![]() $i\in \mathbb {Z}$
:
$i\in \mathbb {Z}$
:
Proof. Note that
![]() $\Omega _{C_S^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^1$
is generated over
$\Omega _{C_S^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^1$
is generated over
![]() $C_S^{\dagger }$
by
$C_S^{\dagger }$
by
![]() $dx_0,\ldots ,x_n,dy_1,\ldots ,dy_k$
and similarly for
$dx_0,\ldots ,x_n,dy_1,\ldots ,dy_k$
and similarly for
![]() $\Omega _{B^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^1$
and
$\Omega _{B^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^1$
and
![]() $\Omega _{A^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^1$
(cf. [Reference Monsky and Washnitzer29, Th. 4.5]). Since
$\Omega _{A^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^1$
(cf. [Reference Monsky and Washnitzer29, Th. 4.5]). Since
![]() $\theta _c$
and
$\theta _c$
and
![]() $\theta _w$
in §2 acts only on
$\theta _w$
in §2 acts only on
![]() $dx$
and
$dx$
and
![]() $dy$
, the proof of Proposition 2.4 works for overconvergent algebras to give the desired decomposition:
$dy$
, the proof of Proposition 2.4 works for overconvergent algebras to give the desired decomposition:
 $$ \begin{align*} \left(\Omega_{C_S^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right). \end{align*} $$
$$ \begin{align*} \left(\Omega_{C_S^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)_{\deg_w=0}=\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right)\oplus\frac{dS}{S}\wedge\left(\Omega_{B^{\dagger}/(\mathcal{O}_{\Bbbk},\mathfrak{m}_{\Bbbk})}^{\bullet},d\right). \end{align*} $$
To get the second assertion, consider the affine weak formal scheme
![]() $(\mathbb {P}(\mathcal {E})\setminus X_S)^{\dagger }$
in the sense of [Reference Meredith24, Def. 15], that is, the topological space
$(\mathbb {P}(\mathcal {E})\setminus X_S)^{\dagger }$
in the sense of [Reference Meredith24, Def. 15], that is, the topological space
![]() $\mathbb {P}(\mathcal {E})\setminus X_{\overline {S}}$
endowed with the structure sheaf associated with
$\mathbb {P}(\mathcal {E})\setminus X_{\overline {S}}$
endowed with the structure sheaf associated with
![]() $A^{\dagger }$
. Then the open subsets for
$A^{\dagger }$
. Then the open subsets for
![]() $j=1,\ldots ,k$
$j=1,\ldots ,k$
give a covering
![]() $\{U_j^{\dagger }\}_{j=1,\ldots ,k}$
of
$\{U_j^{\dagger }\}_{j=1,\ldots ,k}$
of
![]() $(\mathbb {P}(\mathcal {E})\setminus X_S)^{\dagger }$
by principal open subsets associated with the w.c.f.g.
$(\mathbb {P}(\mathcal {E})\setminus X_S)^{\dagger }$
by principal open subsets associated with the w.c.f.g.
![]() $\mathcal {O}_{\Bbbk }$
-algebras
$\mathcal {O}_{\Bbbk }$
-algebras
![]() $(B_j^{\dagger })_{\deg _c=0}$
where
$(B_j^{\dagger })_{\deg _c=0}$
where
![]() $B_j^{\dagger }:=\mathcal {O}_{B_j}^{\dagger }$
. From the vanishing of higher cohomology [Reference Meredith24, Th. 14] of finitely generated modules on affine weak formal schemes, we deduce that the Čech–de Rham complexes of
$B_j^{\dagger }:=\mathcal {O}_{B_j}^{\dagger }$
. From the vanishing of higher cohomology [Reference Meredith24, Th. 14] of finitely generated modules on affine weak formal schemes, we deduce that the Čech–de Rham complexes of
![]() $\mathfrak {m}_{\Bbbk }$
-separated differentials compute the Monsky–Washnitzer cohomology of the corresponding reduction. On the other hand, the section of
$\mathfrak {m}_{\Bbbk }$
-separated differentials compute the Monsky–Washnitzer cohomology of the corresponding reduction. On the other hand, the section of
![]() $\theta _c$
on each
$\theta _c$
on each
![]() $U_j^{\dagger }$
,
$U_j^{\dagger }$
,

as in the proof of Proposition 2.4 still works. Since restriction to a principal open subset is given by tensoring with weakly completed principal localizations (cf. [Reference Meredith24, p. 4]), the Čech–de Rham cosimplicial algebra for
![]() $\mathfrak {m}_{\Bbbk }$
-separated differentials is
$\mathfrak {m}_{\Bbbk }$
-separated differentials is
![]() $0$
-coskeletal as in algebraic de Rham case (Example A.7). Hence, we obtain
$0$
-coskeletal as in algebraic de Rham case (Example A.7). Hence, we obtain
Now, the rest part of the proposition follows from combining the two observations so far.
4.2 Dwork cohomology
In this subsection, we introduce the Dwork complex associated with
![]() $G_1,\ldots ,G_k$
, which gives a p-adic model of twisted de Rham complexes studied in §3. Then, we extend the
$G_1,\ldots ,G_k$
, which gives a p-adic model of twisted de Rham complexes studied in §3. Then, we extend the
![]() $\rho _S$
in Definition 3.1 to the Dwork complex in Proposition 4.11, which proves Theorems 1.1 and 1.2.
$\rho _S$
in Definition 3.1 to the Dwork complex in Proposition 4.11, which proves Theorems 1.1 and 1.2.
Definition 4.8. Denote
 $$ \begin{align*} \mathcal{O}_{\Bbbk}\{z_1,\ldots,z_N\}:=\varprojlim_{\lambda\geq0}\frac{\mathcal{O}_{\Bbbk}[z_1,\ldots,z_N]}{\mathfrak{m}_{\Bbbk}^{\lambda+1}\mathcal{O}_{\Bbbk}[z_1,\ldots,z_N]} \end{align*} $$
$$ \begin{align*} \mathcal{O}_{\Bbbk}\{z_1,\ldots,z_N\}:=\varprojlim_{\lambda\geq0}\frac{\mathcal{O}_{\Bbbk}[z_1,\ldots,z_N]}{\mathfrak{m}_{\Bbbk}^{\lambda+1}\mathcal{O}_{\Bbbk}[z_1,\ldots,z_N]} \end{align*} $$
the ring of restricted power series over
![]() $\mathcal {O}_{\Bbbk }$
(in N variables), and
$\mathcal {O}_{\Bbbk }$
(in N variables), and
the Tate algebra over
![]() $\Bbbk $
(in N variables).
$\Bbbk $
(in N variables).
Remark 4.9. Tate algebra can be written as
 $$ \begin{align*} \Bbbk\{z_1,\ldots,z_N\}=\left\{\sum_{w\in\mathbb{Z}_{\geq0}^{\oplus N}}a_wz^w\in\Bbbk[[z_1,\ldots,z_N]]\ \middle|\ \lim_{|w|\rightarrow\infty}a_w=0\right\}. \end{align*} $$
$$ \begin{align*} \Bbbk\{z_1,\ldots,z_N\}=\left\{\sum_{w\in\mathbb{Z}_{\geq0}^{\oplus N}}a_wz^w\in\Bbbk[[z_1,\ldots,z_N]]\ \middle|\ \lim_{|w|\rightarrow\infty}a_w=0\right\}. \end{align*} $$
Hence, given an N-tuple
![]() $\epsilon =(\epsilon _1,\ldots ,\epsilon _N)$
of positive real numbers, we denote
$\epsilon =(\epsilon _1,\ldots ,\epsilon _N)$
of positive real numbers, we denote
 $$ \begin{align*} \Bbbk\{\epsilon_1^{-1}z_1,\ldots,\epsilon_N^{-1}z_N\}:=\left\{\sum_{w\in\mathbb{Z}_{\geq0}^{\oplus N}}a_wz^w\in\Bbbk[[z_1,\ldots,z_N]]\ \middle|\ \lim_{|w|\rightarrow\infty}a_w\epsilon^w=0\right\}. \end{align*} $$
$$ \begin{align*} \Bbbk\{\epsilon_1^{-1}z_1,\ldots,\epsilon_N^{-1}z_N\}:=\left\{\sum_{w\in\mathbb{Z}_{\geq0}^{\oplus N}}a_wz^w\in\Bbbk[[z_1,\ldots,z_N]]\ \middle|\ \lim_{|w|\rightarrow\infty}a_w\epsilon^w=0\right\}. \end{align*} $$
We sometimes use notation
![]() $\Bbbk \{\epsilon ^{-1}z\}$
. In terms of rigid geometry, this algebra corresponds to the closed polydisk of radius
$\Bbbk \{\epsilon ^{-1}z\}$
. In terms of rigid geometry, this algebra corresponds to the closed polydisk of radius
![]() $\epsilon $
. If
$\epsilon $
. If
![]() $\epsilon =|c|$
for some
$\epsilon =|c|$
for some
![]() $c\in \Bbbk ^{\oplus N}$
, then
$c\in \Bbbk ^{\oplus N}$
, then
 $$ \begin{align*} \Bbbk\{\epsilon^{-1}z\}=\left\{\sum_{w\in\mathbb{Z}_{\geq0}^{\oplus N}}a_wc^{-w}z^w\in\Bbbk[[z]]\ \middle|\ \lim_{|w|\rightarrow\infty}=0\right\}=\Bbbk\{c^{-1}z\}, \end{align*} $$
$$ \begin{align*} \Bbbk\{\epsilon^{-1}z\}=\left\{\sum_{w\in\mathbb{Z}_{\geq0}^{\oplus N}}a_wc^{-w}z^w\in\Bbbk[[z]]\ \middle|\ \lim_{|w|\rightarrow\infty}=0\right\}=\Bbbk\{c^{-1}z\}, \end{align*} $$
where
![]() $\Bbbk \{c^{-1}z\}$
is the Tate algebra with respect to the variables
$\Bbbk \{c^{-1}z\}$
is the Tate algebra with respect to the variables
![]() $c_1^{-1}z_1,\ldots ,c_N^{-1}z_N$
.
$c_1^{-1}z_1,\ldots ,c_N^{-1}z_N$
.
Denote
![]() $N:=n+k+1$
, and denote for
$N:=n+k+1$
, and denote for
![]() $\hbar \in \Bbbk $
with
$\hbar \in \Bbbk $
with
![]() $\mathrm {val}_p\hbar>0$
$\mathrm {val}_p\hbar>0$
 $$ \begin{align*} C(\hbar):=\left\{\sum_{(u,v)\in\mathbb{Z}_{\geq0}^{\oplus N}}a_{u,v}\hbar^{|v|}x^uy^v\in\Bbbk[[x,y]]\ \middle|\ \lim_{|(u,v)|\rightarrow\infty}a_{u,v}=0\right\} \end{align*} $$
$$ \begin{align*} C(\hbar):=\left\{\sum_{(u,v)\in\mathbb{Z}_{\geq0}^{\oplus N}}a_{u,v}\hbar^{|v|}x^uy^v\in\Bbbk[[x,y]]\ \middle|\ \lim_{|(u,v)|\rightarrow\infty}a_{u,v}=0\right\} \end{align*} $$
so that
![]() $C(\hbar )\cong \Bbbk \{x,\hbar y\}$
. Then the twisted de Rham complex of the form
$C(\hbar )\cong \Bbbk \{x,\hbar y\}$
. Then the twisted de Rham complex of the form
will be called the Dwork complex associated with
![]() $G_1,\ldots ,G_k$
, or to
$G_1,\ldots ,G_k$
, or to
![]() $\overline {G}_1,\ldots ,\overline {G}_k$
. The gradings (1.3) is valid on our Dwork complex.
$\overline {G}_1,\ldots ,\overline {G}_k$
. The gradings (1.3) is valid on our Dwork complex.
Notation 4.10. We will often denote
as a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\Bbbk $
-vector space so that
$\Bbbk $
-vector space so that
Now, Theorems 1.1 and 1.2 follow from the following theorem.
Theorem 4.11. If
 $\mathrm {val}_p\gamma \leq \displaystyle \frac {1}{p-1}$
and
$\mathrm {val}_p\gamma \leq \displaystyle \frac {1}{p-1}$
and
![]() $\mathrm {val}_p\hbar>0$
, then the
$\mathrm {val}_p\hbar>0$
, then the
![]() $\rho _S$
in Definition 3.1 extends continuously to p-adic analytic complexes, that is, there is a commutative square
$\rho _S$
in Definition 3.1 extends continuously to p-adic analytic complexes, that is, there is a commutative square

Moreover, the extended
![]() $\rho _S$
induces an isomorphism
$\rho _S$
induces an isomorphism
for every
![]() $i\geq 2$
. On the other hand,
$i\geq 2$
. On the other hand,
Proof. To extend
![]() $\rho _S$
, we need to check the overconvergence of the expression. To see this, it suffices to show that there is some
$\rho _S$
, we need to check the overconvergence of the expression. To see this, it suffices to show that there is some
![]() $r>1$
such that
$r>1$
such that
 $$ \begin{align*} \lim_{|v|\rightarrow\infty}\left(\mathrm{val}_p\left((|v|+|\beta|-1)!\frac{\hbar^{|v|-|\alpha|-|\beta|}}{\gamma^{|v|+|\beta|}}\right)-(|u|+2|v|+|\beta|)\log_pr\right)=\infty. \end{align*} $$
$$ \begin{align*} \lim_{|v|\rightarrow\infty}\left(\mathrm{val}_p\left((|v|+|\beta|-1)!\frac{\hbar^{|v|-|\alpha|-|\beta|}}{\gamma^{|v|+|\beta|}}\right)-(|u|+2|v|+|\beta|)\log_pr\right)=\infty. \end{align*} $$
From the degree condition, we have
Since
![]() $|\alpha |\leq n+1$
and
$|\alpha |\leq n+1$
and
![]() $|\beta |\leq k$
are bounded by constants, we may ignore them so roughly
$|\beta |\leq k$
are bounded by constants, we may ignore them so roughly
![]() $|u|\sim |v|d_{\max }$
for large
$|u|\sim |v|d_{\max }$
for large
![]() $|u|$
. On the other hand, we have
$|u|$
. On the other hand, we have
 $$ \begin{align*} &\quad\mathrm{val}_p\left((|v|+|\beta|-1)!\frac{\hbar^{|v|-|\alpha|-|\beta|}}{\gamma^{|v|+|\beta|}}\right)-(|u|+2|v|+|\beta|)\log_pr\\ &\geq\frac{|v|+|\beta|-1}{p-1}-\log_p(|v|+|\beta|)+\\ &\quad\quad+(|v|-|\alpha|-|\beta|)\mathrm{val}_p\hbar-(|v|+|\beta|)\mathrm{val}_p\gamma-(|u|+2|v|+|\beta|)\log_pr. \end{align*} $$
$$ \begin{align*} &\quad\mathrm{val}_p\left((|v|+|\beta|-1)!\frac{\hbar^{|v|-|\alpha|-|\beta|}}{\gamma^{|v|+|\beta|}}\right)-(|u|+2|v|+|\beta|)\log_pr\\ &\geq\frac{|v|+|\beta|-1}{p-1}-\log_p(|v|+|\beta|)+\\ &\quad\quad+(|v|-|\alpha|-|\beta|)\mathrm{val}_p\hbar-(|v|+|\beta|)\mathrm{val}_p\gamma-(|u|+2|v|+|\beta|)\log_pr. \end{align*} $$
Consequently, it suffices to take r such that
 $$ \begin{align*} 0<\log_pr<\frac{1}{2+d_{\max}}\left(\frac{1}{p-1}+\mathrm{val}_p\hbar-\mathrm{val}_p\gamma\right). \end{align*} $$
$$ \begin{align*} 0<\log_pr<\frac{1}{2+d_{\max}}\left(\frac{1}{p-1}+\mathrm{val}_p\hbar-\mathrm{val}_p\gamma\right). \end{align*} $$
Next, since
![]() $\epsilon _{w,S}$
acts only on
$\epsilon _{w,S}$
acts only on
![]() $dx_0,\ldots ,dx_n,dy_1,\ldots ,dy_k$
, it extends to Dwork complexes. Then, we get a commutative diagram
$dx_0,\ldots ,dx_n,dy_1,\ldots ,dy_k$
, it extends to Dwork complexes. Then, we get a commutative diagram

where the top row is exact by Proposition 3.10. Since the polynomial complexes are dense and the maps are all
![]() $\mathfrak {m}_{\Bbbk }$
-adically continuous, the bottom row is exact as well. Since the relation in Lemma 3.9 holds on
$\mathfrak {m}_{\Bbbk }$
-adically continuous, the bottom row is exact as well. Since the relation in Lemma 3.9 holds on
![]() $\mathscr {L}_{\hbar ,(0,+)}^{\bullet }$
by continuity,
$\mathscr {L}_{\hbar ,(0,+)}^{\bullet }$
by continuity,
![]() $\epsilon _{w,S}$
becomes the zero map on the Dwork cohomology. Therefore, we get an exact sequence
$\epsilon _{w,S}$
becomes the zero map on the Dwork cohomology. Therefore, we get an exact sequence
together with (since
![]() $\overline {\mathcal {O}}_{C_S}=\mathbb {F}_q[x,y,S^{-1}]$
is geometrically connected)
$\overline {\mathcal {O}}_{C_S}=\mathbb {F}_q[x,y,S^{-1}]$
is geometrically connected)
Moreover, since Lemma 3.2 applies to the inclusions
we get the desired vanishing of
![]() $H^1\left (\Omega _{\hbar }^{\bullet },D_{\hbar ,\gamma S}\right )$
. On the other hand, we have
$H^1\left (\Omega _{\hbar }^{\bullet },D_{\hbar ,\gamma S}\right )$
. On the other hand, we have
 $$ \begin{align*} \mathrm{val}_p\left(1+\frac{1}{2}+\cdots+\frac{1}{m}\right)\geq-\log_pm \end{align*} $$
$$ \begin{align*} \mathrm{val}_p\left(1+\frac{1}{2}+\cdots+\frac{1}{m}\right)\geq-\log_pm \end{align*} $$
for every positive integer m so
![]() $\rho _S\chi $
,
$\rho _S\chi $
,
![]() $\rho D_{\hbar ,\gamma S}\chi $
, and
$\rho D_{\hbar ,\gamma S}\chi $
, and
![]() $\rho _S\theta _w\chi $
in Lemmas 3.14 and 3.15, all converge as maps from
$\rho _S\theta _w\chi $
in Lemmas 3.14 and 3.15, all converge as maps from
![]() $\mathscr {L}_{\hbar ,(0,+)}^{\bullet }$
to
$\mathscr {L}_{\hbar ,(0,+)}^{\bullet }$
to
![]() $\Omega _{C_S^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^{\bullet }\otimes _{\mathcal {O}_{\Bbbk }}\Bbbk $
. Therefore, the argument as in Proposition 3.16 works in p-adic setting to give isomorphisms
$\Omega _{C_S^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^{\bullet }\otimes _{\mathcal {O}_{\Bbbk }}\Bbbk $
. Therefore, the argument as in Proposition 3.16 works in p-adic setting to give isomorphisms
Here, we use the identification of Proposition 4.7. Then
![]() $\rho _S$
induces an isomorphism
$\rho _S$
induces an isomorphism
for every
![]() $i\geq 2$
. Note that here we use the canonical isomorphism
$i\geq 2$
. Note that here we use the canonical isomorphism
which exists because
![]() $\mathbb {P}(\mathcal {E})\setminus X_{\overline {S}}$
is smooth affine. Finally, there is an isomorphism
$\mathbb {P}(\mathcal {E})\setminus X_{\overline {S}}$
is smooth affine. Finally, there is an isomorphism
as we have observed in (2.3). Therefore, the proposition follows.
The following corollary is a generalization of Monsky’s remark in [Reference Monsky26, p. 115].
Corollary 4.12. With the assumptions in Proposition 4.11, if
![]() $X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
is a smooth complete intersection, then the inclusion
$X_{\overline {G}}\subseteq \mathbb {P}^n_{\mathbb {F}_q}$
is a smooth complete intersection, then the inclusion
is a quasi-isomorphism.
Proof. By Lemma 3.2, it suffices to show that the inclusion
is a quasi-isomorphism. By Propositions 3.16 and 4.11 together with its proof, this follows if we show that the inclusion
is a quasi-isomorphism. Since
![]() $X_{\underline {G}}$
is smooth and proper,
$X_{\underline {G}}$
is smooth and proper,
and these isomorphisms are compatible with the Gysin sequences for
![]() $H_{\mathrm {dR}}^{\bullet }$
and
$H_{\mathrm {dR}}^{\bullet }$
and
![]() $H_{\mathrm {rig}}^{\bullet }$
, we conclude that the above inclusion of algebraic de Rham complexes coming from
$H_{\mathrm {rig}}^{\bullet }$
, we conclude that the above inclusion of algebraic de Rham complexes coming from
![]() $\mathcal {O}_{\Bbbk }[x,y,S^{-1}]\hookrightarrow C_S^{\dagger }$
is a quasi-isomorphism.
$\mathcal {O}_{\Bbbk }[x,y,S^{-1}]\hookrightarrow C_S^{\dagger }$
is a quasi-isomorphism.
Remark 4.13. The condition on
![]() $\gamma $
given in Proposition 4.11:
$\gamma $
given in Proposition 4.11:
 $$ \begin{align*} 0\leq\mathrm{val}_p\gamma\leq\frac{1}{p-1} \end{align*} $$
$$ \begin{align*} 0\leq\mathrm{val}_p\gamma\leq\frac{1}{p-1} \end{align*} $$
guarantees that
is a subring of
![]() $C(\hbar )$
. Then
$C(\hbar )$
. Then
is an
![]() $C(\hbar \gamma )$
-submodule of
$C(\hbar \gamma )$
-submodule of
![]() $\Omega _{\hbar }^{\bullet }$
. Arguing as in the proof of Proposition 4.11, we see that all inclusions
$\Omega _{\hbar }^{\bullet }$
. Arguing as in the proof of Proposition 4.11, we see that all inclusions
are quasi-isomorphisms. On the other hand,
![]() $C(\hbar \gamma )$
admits a filtration
$C(\hbar \gamma )$
admits a filtration
 $$ \begin{align*} F^eC(\hbar\gamma):=\left\{\sum_{(u,v)\in\mathbb{Z}_{\geq0}^{\oplus N}}a_{u,v}(\hbar\gamma)^{|v|}x^uy^v\in C(\hbar)\ \middle|\ a_{u,v}\in\pi^e\mathcal{O}_{\Bbbk}\right\} \end{align*} $$
$$ \begin{align*} F^eC(\hbar\gamma):=\left\{\sum_{(u,v)\in\mathbb{Z}_{\geq0}^{\oplus N}}a_{u,v}(\hbar\gamma)^{|v|}x^uy^v\in C(\hbar)\ \middle|\ a_{u,v}\in\pi^e\mathcal{O}_{\Bbbk}\right\} \end{align*} $$
which induces a ring isomorphism
 $$ \begin{align*} \mathbb{F}_q[x,y]\cong\frac{\mathcal{O}_{\Bbbk}\{x,y\}}{\pi\mathcal{O}_{\Bbbk}\{x,y\}}\cong\frac{F^0C(\hbar\gamma)}{F^1C(\hbar\gamma)}. \end{align*} $$
$$ \begin{align*} \mathbb{F}_q[x,y]\cong\frac{\mathcal{O}_{\Bbbk}\{x,y\}}{\pi\mathcal{O}_{\Bbbk}\{x,y\}}\cong\frac{F^0C(\hbar\gamma)}{F^1C(\hbar\gamma)}. \end{align*} $$
The filtration on
![]() $C(\hbar \gamma )$
extends to
$C(\hbar \gamma )$
extends to
given as follows:
 $$ \begin{align*} F^e\Omega_{\hbar\gamma}^m:=\bigoplus_{i+j=m}\bigoplus_{\substack{0\leq\alpha_1<\cdots<\alpha_i\leq n \\ 1\leq\beta_1<\cdots<\beta_j\leq k}}(\hbar\gamma)^jF^eC(\hbar\gamma)dx_{\alpha_1}\wedge\cdots\wedge dx_{\alpha_i}\wedge dy_{\beta_1}\wedge\cdots\wedge dy_{\beta_j}. \end{align*} $$
$$ \begin{align*} F^e\Omega_{\hbar\gamma}^m:=\bigoplus_{i+j=m}\bigoplus_{\substack{0\leq\alpha_1<\cdots<\alpha_i\leq n \\ 1\leq\beta_1<\cdots<\beta_j\leq k}}(\hbar\gamma)^jF^eC(\hbar\gamma)dx_{\alpha_1}\wedge\cdots\wedge dx_{\alpha_i}\wedge dy_{\beta_1}\wedge\cdots\wedge dy_{\beta_j}. \end{align*} $$
Then the above ring isomorphism extends to the isomorphism

where we denote
![]() $\overline {S}\in \mathbb {F}_q[x,y]$
the reduction of S. By this observation, we may apply [Reference Adolphson and Sperber5, Prop. A.2] to lift a basis for the cohomology of
$\overline {S}\in \mathbb {F}_q[x,y]$
the reduction of S. By this observation, we may apply [Reference Adolphson and Sperber5, Prop. A.2] to lift a basis for the cohomology of
![]() $\left (\Omega _{\mathbb {F}_q[x,y]/\mathbb {F}_q}^{\bullet },d\overline {S}\wedge -\right )$
to get a basis for the cohomology of
$\left (\Omega _{\mathbb {F}_q[x,y]/\mathbb {F}_q}^{\bullet },d\overline {S}\wedge -\right )$
to get a basis for the cohomology of
![]() $\left (\Omega _{\hbar }^{\bullet },D_{\hbar ,\gamma S}\right )$
whenever the cohomology over the residue field is finite-dimensional. For the detailed computation over the residue field when
$\left (\Omega _{\hbar }^{\bullet },D_{\hbar ,\gamma S}\right )$
whenever the cohomology over the residue field is finite-dimensional. For the detailed computation over the residue field when
![]() $\overline {G}_1,\ldots ,\overline {G}_k$
define a smooth projective complete intersection, see [Reference Adolphson and Sperber4].
$\overline {G}_1,\ldots ,\overline {G}_k$
define a smooth projective complete intersection, see [Reference Adolphson and Sperber4].
5 Operators on p-adic analytic cohomologies
In this section, we will give more precise statement of Theorem 1.3 together with its detailed proof. This section is a generalization of [Reference Katz19, §III]. We begin with reviewing some necessary constructions. For each
![]() $i\geq 1$
, the equation
$i\geq 1$
, the equation
 $$ \begin{align*} t+\frac{t^p}{p}+\frac{t^{p^2}}{p^2}+\cdots+\frac{t^{p^i}}{p^i}=0 \end{align*} $$
$$ \begin{align*} t+\frac{t^p}{p}+\frac{t^{p^2}}{p^2}+\cdots+\frac{t^{p^i}}{p^i}=0 \end{align*} $$
has a solution
![]() $\gamma _i$
with
$\gamma _i$
with
 $$ \begin{align*} \mathrm{val}_p\gamma_i=\frac{1}{p-1}. \end{align*} $$
$$ \begin{align*} \mathrm{val}_p\gamma_i=\frac{1}{p-1}. \end{align*} $$
For each choice of
![]() $\gamma _i$
, the corresponding Dwork’s splitting functions is defined to be
$\gamma _i$
, the corresponding Dwork’s splitting functions is defined to be
 $$ \begin{align*} \theta_i(t):=\exp\left(\gamma_it+\frac{(\gamma_it)^p}{p}+\frac{(\gamma_it)^{p^2}}{p^2}+\cdots+\frac{(\gamma_it)^{p^i}}{p^i}\right). \end{align*} $$
$$ \begin{align*} \theta_i(t):=\exp\left(\gamma_it+\frac{(\gamma_it)^p}{p}+\frac{(\gamma_it)^{p^2}}{p^2}+\cdots+\frac{(\gamma_it)^{p^i}}{p^i}\right). \end{align*} $$
Each
![]() $\theta _i$
has integral coefficients and converges for
$\theta _i$
has integral coefficients and converges for
 $$ \begin{align*} \mathrm{val}_pt>-\frac{1}{p-1}+\frac{1}{p^{i+1}}\left(i+1+\frac{1}{p-1}\right). \end{align*} $$
$$ \begin{align*} \mathrm{val}_pt>-\frac{1}{p-1}+\frac{1}{p^{i+1}}\left(i+1+\frac{1}{p-1}\right). \end{align*} $$
In this section, we will take
![]() $\gamma =\gamma _1$
so that
$\gamma =\gamma _1$
so that
![]() $\gamma ^{p-1}=-p$
and
$\gamma ^{p-1}=-p$
and
 $$ \begin{align*} \theta_1(t)=\exp\left(\gamma t+\frac{\gamma^pt^p}{p}\right)=\exp(\gamma t-\gamma t^p). \end{align*} $$
$$ \begin{align*} \theta_1(t)=\exp\left(\gamma t+\frac{\gamma^pt^p}{p}\right)=\exp(\gamma t-\gamma t^p). \end{align*} $$
If
![]() $q=p^a$
, then
$q=p^a$
, then
converges for
 $$ \begin{align*} \mathrm{val}_pt>\frac{1-p}{pq}. \end{align*} $$
$$ \begin{align*} \mathrm{val}_pt>\frac{1-p}{pq}. \end{align*} $$
In this section, we denote for a nonzero
![]() $F\in \mathcal {O}_{\Bbbk }[x,y]$
by
$F\in \mathcal {O}_{\Bbbk }[x,y]$
by
![]() $ C_F^{\dagger }:=\mathcal {O}_{\Bbbk }\{x,y,F^{-1}\}^{\dagger }$
, the corresponding weakly complete finitely generated algebra over
$ C_F^{\dagger }:=\mathcal {O}_{\Bbbk }\{x,y,F^{-1}\}^{\dagger }$
, the corresponding weakly complete finitely generated algebra over
![]() $\mathcal {O}_{\Bbbk }$
. Still we mainly consider
$\mathcal {O}_{\Bbbk }$
. Still we mainly consider
![]() $S:=y_1G_1+\cdots +y_kG_k$
, where each
$S:=y_1G_1+\cdots +y_kG_k$
, where each
![]() $G_i$
is not divisible by the uniformizer
$G_i$
is not divisible by the uniformizer
![]() $\pi \in \mathfrak {m}_{\Bbbk }$
, in which case, we denote
$\pi \in \mathfrak {m}_{\Bbbk }$
, in which case, we denote
![]() $\rho _S$
the cochain map as in Proposition 4.11. The following lemma is an analog of [Reference Katz19, Lem. 2.13].
$\rho _S$
the cochain map as in Proposition 4.11. The following lemma is an analog of [Reference Katz19, Lem. 2.13].
Lemma 5.1. Let
![]() $S,T\in \mathcal {O}_{\Bbbk }[x,y]$
be homogeneous with respect to
$S,T\in \mathcal {O}_{\Bbbk }[x,y]$
be homogeneous with respect to
![]() $\deg _w$
. If S and T are of
$\deg _w$
. If S and T are of
![]() $\deg _w=1$
, and
$\deg _w=1$
, and
![]() $S-T\equiv 0\bmod \pi $
, then
$S-T\equiv 0\bmod \pi $
, then

is commutative.
Proof. Note that if
![]() $S-T\equiv 0\bmod \pi $
, then
$S-T\equiv 0\bmod \pi $
, then
 $$ \begin{align*} \frac{1}{T}=\frac{1}{\displaystyle S\left(1-\frac{S-T}{S}\right)}=\sum_{m\geq0}\frac{(S-T)^m}{S^{m+1}} \end{align*} $$
$$ \begin{align*} \frac{1}{T}=\frac{1}{\displaystyle S\left(1-\frac{S-T}{S}\right)}=\sum_{m\geq0}\frac{(S-T)^m}{S^{m+1}} \end{align*} $$
converges in
![]() $C_S^{\dagger }$
so
$C_S^{\dagger }$
so
![]() $C_S^{\dagger }\cong C_T^{\dagger }$
are canonically identified. Then the commutativity follows from direct computation:
$C_S^{\dagger }\cong C_T^{\dagger }$
are canonically identified. Then the commutativity follows from direct computation:
 $$ \begin{align*} &\quad\rho_T\left(\exp(\gamma S-\gamma T)x^u(\hbar y)^vdx_{\alpha}\wedge dy_{\beta}\right)=\rho_T\left(\sum_{m\geq0}\frac{\gamma^m}{m!}(S-T)^mx^u(\hbar y)^vdx_{\alpha}\wedge dy_{\beta}\right)\\ &=\sum_{m\geq0}\frac{\gamma^m}{m!}(-1)^{m+|v|+|\beta|-1}(m+|v|+|\beta|-1)!\frac{(S-T)^m}{\gamma^mT^m}\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\sum_{m\geq0}\binom{-|v|-|\beta|}{m}\left(\frac{S-T}{T}\right)^m\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\left(1+\frac{S-T}{T}\right)^{-|v|-|\beta|}\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{T^{|v|+|\beta|}}{S^{|v|+|\beta|}}\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\\ &=\rho_S\left(x^u(\hbar y)^vdx_{\alpha}\wedge dy_{\beta}\right). \end{align*} $$
$$ \begin{align*} &\quad\rho_T\left(\exp(\gamma S-\gamma T)x^u(\hbar y)^vdx_{\alpha}\wedge dy_{\beta}\right)=\rho_T\left(\sum_{m\geq0}\frac{\gamma^m}{m!}(S-T)^mx^u(\hbar y)^vdx_{\alpha}\wedge dy_{\beta}\right)\\ &=\sum_{m\geq0}\frac{\gamma^m}{m!}(-1)^{m+|v|+|\beta|-1}(m+|v|+|\beta|-1)!\frac{(S-T)^m}{\gamma^mT^m}\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\sum_{m\geq0}\binom{-|v|-|\beta|}{m}\left(\frac{S-T}{T}\right)^m\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\left(1+\frac{S-T}{T}\right)^{-|v|-|\beta|}\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{T^{|v|+|\beta|}}{S^{|v|+|\beta|}}\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}T^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}T^{|\beta|}}\\ &=(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{\hbar^{|v|}x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\\ &=\rho_S\left(x^u(\hbar y)^vdx_{\alpha}\wedge dy_{\beta}\right). \end{align*} $$
5.1 The Frobenius operator
Denote
![]() $\mathrm {Fr}$
the endomorphism on
$\mathrm {Fr}$
the endomorphism on
![]() $C_S^{\dagger }$
lifting the qth power endomorphism over the residue field such that
$C_S^{\dagger }$
lifting the qth power endomorphism over the residue field such that
This map is injective and extends to a cochain map
Note that the above
![]() $\mathrm {Fr}$
sends the bidegree
$\mathrm {Fr}$
sends the bidegree
![]() $(c,w)$
-subspace to the bidegree
$(c,w)$
-subspace to the bidegree
![]() $(qc,qw)$
-subspace. Hence, our
$(qc,qw)$
-subspace. Hence, our
![]() $\mathrm {Fr}$
restricts to the bidegree
$\mathrm {Fr}$
restricts to the bidegree
![]() $(0,0)$
-subcomplex:
$(0,0)$
-subcomplex:
On the other hand, denote

then
![]() $\Phi _q$
satisfies
$\Phi _q$
satisfies
 $$ \begin{align*} z_i\frac{\partial}{\partial z_i}\circ\Phi_q=q\Phi_q\circ z_i\frac{\partial}{\partial z_i}. \end{align*} $$
$$ \begin{align*} z_i\frac{\partial}{\partial z_i}\circ\Phi_q=q\Phi_q\circ z_i\frac{\partial}{\partial z_i}. \end{align*} $$
Using this, we may extend
![]() $\Phi _q$
to the cochain map as follows:
$\Phi _q$
to the cochain map as follows:
with the
![]() $\Bbbk $
-linearity. We may write
$\Bbbk $
-linearity. We may write
 $$ \begin{align*} \Phi_{q,\mathbb{P}^n_{\Bbbk}}(fdx_{\alpha}\wedge dy_{\beta})&=\Phi_q(f)q^{|\alpha|}x_{\alpha}^{q-1}dx_{\alpha}\wedge q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}\\ &=\frac{1}{x_{\alpha} y_{\alpha}}\Phi_q(x_{\alpha} y_{\beta} f)q^{|\alpha|}dx_{\alpha}\wedge q^{|\beta|}dy_{\beta}, \end{align*} $$
$$ \begin{align*} \Phi_{q,\mathbb{P}^n_{\Bbbk}}(fdx_{\alpha}\wedge dy_{\beta})&=\Phi_q(f)q^{|\alpha|}x_{\alpha}^{q-1}dx_{\alpha}\wedge q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}\\ &=\frac{1}{x_{\alpha} y_{\alpha}}\Phi_q(x_{\alpha} y_{\beta} f)q^{|\alpha|}dx_{\alpha}\wedge q^{|\beta|}dy_{\beta}, \end{align*} $$
where we extend convention (1.4) to monomials:

For
![]() $S:=y_1G_1+\cdots +y_kG_k$
as before, define
$S:=y_1G_1+\cdots +y_kG_k$
as before, define
by the formal identity
which converges because we can rewrite
 $$ \begin{align*} \Phi_{q,S}&=\exp(\gamma\mathrm{Fr}(S)-\gamma S)\circ\Phi_{q,\mathbb{P}^n_{\Bbbk}}\\ &=\left(\prod_{i=1}^k\exp\left(\gamma y_i^q\mathrm{Fr}_xG_i-\gamma y_i^qG_i^q\right)\exp\left(\gamma y_i^qG_i^q-\gamma y_iG_i\right)\right)\circ\Phi_{q,\mathbb{P}^n_{\Bbbk}} \end{align*} $$
$$ \begin{align*} \Phi_{q,S}&=\exp(\gamma\mathrm{Fr}(S)-\gamma S)\circ\Phi_{q,\mathbb{P}^n_{\Bbbk}}\\ &=\left(\prod_{i=1}^k\exp\left(\gamma y_i^q\mathrm{Fr}_xG_i-\gamma y_i^qG_i^q\right)\exp\left(\gamma y_i^qG_i^q-\gamma y_iG_i\right)\right)\circ\Phi_{q,\mathbb{P}^n_{\Bbbk}} \end{align*} $$
and the final expression converges. Since we may formally write
![]() $\Phi _{q,S}$
is still a cochain map. Now, we may compare
$\Phi _{q,S}$
is still a cochain map. Now, we may compare
![]() $\mathrm {Fr}$
and
$\mathrm {Fr}$
and
![]() $\Phi _{q,S}$
via
$\Phi _{q,S}$
via
![]() $\rho _S$
.
$\rho _S$
.
Proposition 5.2. There is a commutative diagram

Proof. We will follow Katz’s computation in the proof of [Reference Katz19, Th. 2.14] and [Reference Katz19, Th. 2.8]. Since the Frobenius on
![]() $\mathbb {F}_q[x,y]$
can be decomposed into
$\mathbb {F}_q[x,y]$
can be decomposed into

where the superscript
![]() $(q)$
on each ring means that
$(q)$
on each ring means that
![]() $\mathbb {F}_q$
acts by qth power. Denote the lifting of each factor by
$\mathbb {F}_q$
acts by qth power. Denote the lifting of each factor by
We abuse notation to denote
![]() $\mathrm {Fr}_GS:=y_1G_1^q+\cdots +y_kG_k^q$
. Then there is a diagram
$\mathrm {Fr}_GS:=y_1G_1^q+\cdots +y_kG_k^q$
. Then there is a diagram

where in the second and the third rows, we set
![]() $\deg _cy_i:=-qd_i$
. The top square is commutative because
$\deg _cy_i:=-qd_i$
. The top square is commutative because
 $$ \begin{align*} &(\mathrm{Fr}_x\circ\rho_S)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_x\left(\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_xS^{|v|}}\frac{q^{|\alpha|}x_{\alpha}^{q-1}dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_xS^{|\beta|}}\\& \quad =\rho_{\mathrm{Fr}_xS}\left(q^{|\alpha|}x_{\alpha}^{q-1}x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\& \quad =\left(\rho_{\mathrm{Fr}_xS}\circ\Phi_{q,\mathbb{P}^n_{\Bbbk}}^x\right)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right). \end{align*} $$
$$ \begin{align*} &(\mathrm{Fr}_x\circ\rho_S)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_x\left(\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_xS^{|v|}}\frac{q^{|\alpha|}x_{\alpha}^{q-1}dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_xS^{|\beta|}}\\& \quad =\rho_{\mathrm{Fr}_xS}\left(q^{|\alpha|}x_{\alpha}^{q-1}x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\& \quad =\left(\rho_{\mathrm{Fr}_xS}\circ\Phi_{q,\mathbb{P}^n_{\Bbbk}}^x\right)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right). \end{align*} $$
The middle square is commutative by Lemma 5.1. For the bottom square, we first compute
 $$ \begin{align*} &\left(\mathrm{Fr}_y\circ\rho_{\mathrm{Fr}_GS}\right)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_y\left(\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_GS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_GS^{|\beta|}}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^{qv}}{\gamma^{|v|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|\beta|}}. \end{align*} $$
$$ \begin{align*} &\left(\mathrm{Fr}_y\circ\rho_{\mathrm{Fr}_GS}\right)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_y\left(\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_GS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_GS^{|\beta|}}\right)\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{x^uy^{qv}}{\gamma^{|v|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|\beta|}}. \end{align*} $$
If we write
 $$ \begin{align*} \exp(\gamma t^q-\gamma t)=\sum_{m\geq0}a_mt^m, \end{align*} $$
$$ \begin{align*} \exp(\gamma t^q-\gamma t)=\sum_{m\geq0}a_mt^m, \end{align*} $$
then
 $$ \begin{align*} &\rho_S\left(q\exp(\gamma\mathrm{Fr}_y\mathrm{Fr}_GS-\gamma S)\Phi_{q,\mathbb{P}^n_{\Bbbk}}^y\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\right)\\& \quad =\rho_S\left(q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_{m_1}\ldots a_{m_k}(y_1G_1)^{m_1}\ldots(y_kG_k)^{m_k}x^uy^{qv}dx_{\alpha}\wedge q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}\right)\\& \quad =q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+q|v|+q|\beta|-1}(|m|+q|v|+q|\beta|-1)!\frac{(yG)^m}{\gamma^{|m|}S^{|m|}}\frac{x^uy^{q|v|}}{\gamma^{q|v|}S^{q|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}}{\hbar^{|\beta|}\gamma^{q|\beta|}S^{q|\beta|}}\\& \quad =q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+q|v|+q|\beta|-1}(|m|+q|v|+q|\beta|-1)!\frac{(yG)^m}{\gamma^{|m|}S^{|m|}}\frac{\gamma^{|v|+|\beta|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|v|+|\beta|}}{\gamma^{q|v|+q|\beta|}S^{q|v|+q|\beta|}}\times\\&\qquad\times\mathrm{Fr}_y\left(\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_GS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_GS^{|\beta|}}\right). \end{align*} $$
$$ \begin{align*} &\rho_S\left(q\exp(\gamma\mathrm{Fr}_y\mathrm{Fr}_GS-\gamma S)\Phi_{q,\mathbb{P}^n_{\Bbbk}}^y\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\right)\\& \quad =\rho_S\left(q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_{m_1}\ldots a_{m_k}(y_1G_1)^{m_1}\ldots(y_kG_k)^{m_k}x^uy^{qv}dx_{\alpha}\wedge q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}\right)\\& \quad =q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+q|v|+q|\beta|-1}(|m|+q|v|+q|\beta|-1)!\frac{(yG)^m}{\gamma^{|m|}S^{|m|}}\frac{x^uy^{q|v|}}{\gamma^{q|v|}S^{q|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{q^{|\beta|}y_{\beta}^{q-1}dy_{\beta}}{\hbar^{|\beta|}\gamma^{q|\beta|}S^{q|\beta|}}\\& \quad =q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+q|v|+q|\beta|-1}(|m|+q|v|+q|\beta|-1)!\frac{(yG)^m}{\gamma^{|m|}S^{|m|}}\frac{\gamma^{|v|+|\beta|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|v|+|\beta|}}{\gamma^{q|v|+q|\beta|}S^{q|v|+q|\beta|}}\times\\&\qquad\times\mathrm{Fr}_y\left(\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_GS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_GS^{|\beta|}}\right). \end{align*} $$
Hence, the commutativity follows if we show that
 $$ \begin{align} \begin{aligned} & q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+q|v|+q|\beta|-1}(|m|+q|v|+q|\beta|-1)!\frac{(yG)^m}{\gamma^{|m|}S^{|m|}}\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{\gamma^{q|v|+q|\beta|}S^{q|v|+q|\beta|}}{\gamma^{|v|+|\beta|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|v|+|\beta|}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & q\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+q|v|+q|\beta|-1}(|m|+q|v|+q|\beta|-1)!\frac{(yG)^m}{\gamma^{|m|}S^{|m|}}\\& \quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{\gamma^{q|v|+q|\beta|}S^{q|v|+q|\beta|}}{\gamma^{|v|+|\beta|}\mathrm{Fr}_y\mathrm{Fr}_GS^{|v|+|\beta|}}. \end{aligned} \end{align} $$
To do this, consider
 $$ \begin{align*} f(t)&:=t^{qw-1}\exp\left(\frac{\mathrm{Fr}_y\mathrm{Fr}_GS\cdot t^q}{\gamma^{q-1}S^q}-t\right)\\ &=t^{qw-1}\prod_{i=1}^k\exp\left(\frac{(y_iG_i)^qt^q}{\gamma^{q-1}S^q}-\frac{y_iG_it}{S}\right)\\ &=t^{qw-1}\prod_{i=1}^k\sum_{m\geq0}a_m\frac{(y_iG_i)^mt^m}{S^m}=\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m\frac{(yG)^mt^{|m|+qw-1}}{S^{|m|}} \end{align*} $$
$$ \begin{align*} f(t)&:=t^{qw-1}\exp\left(\frac{\mathrm{Fr}_y\mathrm{Fr}_GS\cdot t^q}{\gamma^{q-1}S^q}-t\right)\\ &=t^{qw-1}\prod_{i=1}^k\exp\left(\frac{(y_iG_i)^qt^q}{\gamma^{q-1}S^q}-\frac{y_iG_it}{S}\right)\\ &=t^{qw-1}\prod_{i=1}^k\sum_{m\geq0}a_m\frac{(y_iG_i)^mt^m}{S^m}=\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m\frac{(yG)^mt^{|m|+qw-1}}{S^{|m|}} \end{align*} $$
and
 $$ \begin{align*} g(t):=\sum_{\ell\geq0}(-1)^{\ell}\frac{d^{\ell} f}{dt^{\ell}}. \end{align*} $$
$$ \begin{align*} g(t):=\sum_{\ell\geq0}(-1)^{\ell}\frac{d^{\ell} f}{dt^{\ell}}. \end{align*} $$
Note that g satisfies
 $$ \begin{align*} g(0)=\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+qw-1}(|m|+qw-1)!\frac{(yG)^m}{S^{|m|}}. \end{align*} $$
$$ \begin{align*} g(0)=\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+qw-1}(|m|+qw-1)!\frac{(yG)^m}{S^{|m|}}. \end{align*} $$
Moreover, g is by definition a formal solution of the differential equation
which converges for
 $\displaystyle \mathrm {val}_pt>\frac {1}{p-1}-\frac {p-1}{pq}$
. Since the only solution of
$\displaystyle \mathrm {val}_pt>\frac {1}{p-1}-\frac {p-1}{pq}$
. Since the only solution of
is a constant multiple of
![]() $\exp (-t)$
which converges only for
$\exp (-t)$
which converges only for
 $\displaystyle \mathrm {val}_pt>\frac {1}{p-1}$
, g is the unique power series solution. On the other hand, there is a solution of the form
$\displaystyle \mathrm {val}_pt>\frac {1}{p-1}$
, g is the unique power series solution. On the other hand, there is a solution of the form
 $$ \begin{align*} h(t^q)\exp\left(\frac{\mathrm{Fr}_y\mathrm{Fr}_GS\cdot t^q}{\gamma^{q-1}S^q}-t\right). \end{align*} $$
$$ \begin{align*} h(t^q)\exp\left(\frac{\mathrm{Fr}_y\mathrm{Fr}_GS\cdot t^q}{\gamma^{q-1}S^q}-t\right). \end{align*} $$
After substituting and dividing by the exponential, we get
 $$ \begin{align*} h(t^q)+\frac{d}{dt}h(t^q)+\left(\frac{q\mathrm{Fr}_y\mathrm{Fr}_GS\cdot t^{q-1}}{\gamma^{q-1}S^q}-1\right)h(t^q)=t^{qw-1}, \end{align*} $$
$$ \begin{align*} h(t^q)+\frac{d}{dt}h(t^q)+\left(\frac{q\mathrm{Fr}_y\mathrm{Fr}_GS\cdot t^{q-1}}{\gamma^{q-1}S^q}-1\right)h(t^q)=t^{qw-1}, \end{align*} $$
which is equivalent to
 $$ \begin{align*} \frac{q\mathrm{Fr}_y\mathrm{Fr}_GS}{\gamma^{q-1}S^q}t^qh(t^q)+t\frac{d}{dt}h(t^q)=t^{qw}. \end{align*} $$
$$ \begin{align*} \frac{q\mathrm{Fr}_y\mathrm{Fr}_GS}{\gamma^{q-1}S^q}t^qh(t^q)+t\frac{d}{dt}h(t^q)=t^{qw}. \end{align*} $$
By change of variables, it is equivalent to
 $$ \begin{align*} \frac{q\mathrm{Fr}_y\mathrm{Fr}_GS}{\gamma^{q-1}S^q}th(t)+qt\frac{d}{dt}h(t)=t^w. \end{align*} $$
$$ \begin{align*} \frac{q\mathrm{Fr}_y\mathrm{Fr}_GS}{\gamma^{q-1}S^q}th(t)+qt\frac{d}{dt}h(t)=t^w. \end{align*} $$
Hence, we may write
 $$ \begin{align*} h(t)=\left(1+\frac{\gamma^{q-1}S^q}{\mathrm{Fr}_y\mathrm{Fr}_GS}\frac{d}{dt}\right)^{-1}\left(\frac{\gamma^{q-1}S^q}{q\mathrm{Fr}_y\mathrm{Fr}_GS}t^{w-1}\right) \end{align*} $$
$$ \begin{align*} h(t)=\left(1+\frac{\gamma^{q-1}S^q}{\mathrm{Fr}_y\mathrm{Fr}_GS}\frac{d}{dt}\right)^{-1}\left(\frac{\gamma^{q-1}S^q}{q\mathrm{Fr}_y\mathrm{Fr}_GS}t^{w-1}\right) \end{align*} $$
with the condition
 $$ \begin{align*} h(0)=(-1)^{w-1}(w-1)!\frac{\gamma^{qw}S^{qw}}{q\gamma^w\mathrm{Fr}_y\mathrm{Fr}_GS^w}. \end{align*} $$
$$ \begin{align*} h(0)=(-1)^{w-1}(w-1)!\frac{\gamma^{qw}S^{qw}}{q\gamma^w\mathrm{Fr}_y\mathrm{Fr}_GS^w}. \end{align*} $$
Therefore, since
![]() $g(0)=h(0)$
by the observation so far,
$g(0)=h(0)$
by the observation so far,
 $$ \begin{align*} \sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+qw-1}(|m|+qw-1)!\frac{(yG)^m}{S^{|m|}}=(-1)^{w-1}(w-1)!\frac{\gamma^{qw}S^{qw}}{q\gamma^w\mathrm{Fr}_y\mathrm{Fr}_GS^w}. \end{align*} $$
$$ \begin{align*} \sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}a_m(-1)^{|m|+qw-1}(|m|+qw-1)!\frac{(yG)^m}{S^{|m|}}=(-1)^{w-1}(w-1)!\frac{\gamma^{qw}S^{qw}}{q\gamma^w\mathrm{Fr}_y\mathrm{Fr}_GS^w}. \end{align*} $$
Substituting
![]() $w=|v|+|\beta |$
, we get equality (5.1), and the proof is completed.
$w=|v|+|\beta |$
, we get equality (5.1), and the proof is completed.
5.2 The Dwork operator
Since
![]() $\mathrm {Fr}(C_S^{\dagger })\subseteq C_S^{\dagger }$
is a finite locally free ring extension of integral domains, there is a cochain map
$\mathrm {Fr}(C_S^{\dagger })\subseteq C_S^{\dagger }$
is a finite locally free ring extension of integral domains, there is a cochain map
as in [Reference Van der Put32, Prop. 3.1]. Denote
![]() $\psi $
the composite
$\psi $
the composite
that is, the unique map satisfying
![]() $\mathrm {Fr}\circ \psi =\mathrm {Tr}$
. By the description of [Reference Van der Put32, Prop. 3.1],
$\mathrm {Fr}\circ \psi =\mathrm {Tr}$
. By the description of [Reference Van der Put32, Prop. 3.1],
![]() $\mathrm {Tr}$
on the differential forms fits into the commutative diagram
$\mathrm {Tr}$
on the differential forms fits into the commutative diagram

where the isomorphism comes from the inclusion
![]() $\Omega _{\mathrm {Fr}(C_S^{\dagger })/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^{\bullet }\subseteq \Omega _{C_S^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^{\bullet }$
, and
$\Omega _{\mathrm {Fr}(C_S^{\dagger })/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^{\bullet }\subseteq \Omega _{C_S^{\dagger }/(\mathcal {O}_{\Bbbk },\mathfrak {m}_{\Bbbk })}^{\bullet }$
, and
![]() $\mathrm {Tr}:K(C_S^{\dagger })\rightarrow K(\mathrm {Fr}(C_S^{\dagger }))$
is the usual trace map for fields extends of finite degree. This gives a description of
$\mathrm {Tr}:K(C_S^{\dagger })\rightarrow K(\mathrm {Fr}(C_S^{\dagger }))$
is the usual trace map for fields extends of finite degree. This gives a description of
![]() $\psi $
:
$\psi $
:
 $$ \begin{align*} \psi\left(fdx_{\alpha}\wedge dy_{\beta}\right)&=\psi\left(\frac{f}{x_{\alpha}^{q-1}y_{\beta}^{q-1}}\frac{dx_{\alpha}^q}{q^{|\alpha|}}\wedge\frac{dy_{\beta}^q}{q^{|\beta|}}\right)\\ &=\mathrm{Fr}^{-1}\left(\mathrm{Tr}\left(\frac{f}{x_{\alpha}^{q-1}y_{\beta}^{q-1}}\right)\frac{dx_{\alpha}^q}{q^{|\alpha|}}\wedge\frac{dy_{\beta}^q}{q^{|\beta|}}\right)\\ &=\mathrm{Fr}^{-1}\left(\mathrm{Tr}\left(\frac{f}{x_{\alpha}^{q-1}y_{\beta}^{q-1}}\right)\right)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge\frac{dy_{\beta}}{q^{|\beta|}}, \end{align*} $$
$$ \begin{align*} \psi\left(fdx_{\alpha}\wedge dy_{\beta}\right)&=\psi\left(\frac{f}{x_{\alpha}^{q-1}y_{\beta}^{q-1}}\frac{dx_{\alpha}^q}{q^{|\alpha|}}\wedge\frac{dy_{\beta}^q}{q^{|\beta|}}\right)\\ &=\mathrm{Fr}^{-1}\left(\mathrm{Tr}\left(\frac{f}{x_{\alpha}^{q-1}y_{\beta}^{q-1}}\right)\frac{dx_{\alpha}^q}{q^{|\alpha|}}\wedge\frac{dy_{\beta}^q}{q^{|\beta|}}\right)\\ &=\mathrm{Fr}^{-1}\left(\mathrm{Tr}\left(\frac{f}{x_{\alpha}^{q-1}y_{\beta}^{q-1}}\right)\right)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge\frac{dy_{\beta}}{q^{|\beta|}}, \end{align*} $$
where, following (1.4), we denote

By our choice of
![]() $\mathrm {Fr}$
in §5.1,
$\mathrm {Fr}$
in §5.1,
![]() $\mathrm {Fr}^{-1}$
sends the bidegree
$\mathrm {Fr}^{-1}$
sends the bidegree
![]() $(qc,qw)$
-subspace to the bidegree
$(qc,qw)$
-subspace to the bidegree
![]() $(c,w)$
-subspace. Hence, the corresponding
$(c,w)$
-subspace. Hence, the corresponding
![]() $\mathrm {Tr}$
restricts to the bidegree
$\mathrm {Tr}$
restricts to the bidegree
![]() $(0,0)$
-subcomplex; and hence, our
$(0,0)$
-subcomplex; and hence, our
![]() $\psi $
restricts to the bidegree
$\psi $
restricts to the bidegree
![]() $(0,0)$
-subcomplex:
$(0,0)$
-subcomplex:
On the other hand, denote

then
![]() $\Psi _q$
satisfies
$\Psi _q$
satisfies
 $$ \begin{align*} \Psi_q\circ z_i\frac{\partial}{\partial z_i}=qz_i\frac{\partial}{\partial z_i}\circ\Psi_q. \end{align*} $$
$$ \begin{align*} \Psi_q\circ z_i\frac{\partial}{\partial z_i}=qz_i\frac{\partial}{\partial z_i}\circ\Psi_q. \end{align*} $$
Using this, we may extend
![]() $\Psi _q$
to the cochain map analogously to
$\Psi _q$
to the cochain map analogously to
![]() $\Phi _{q,\mathbb {P}^n_{\Bbbk }}$
:
$\Phi _{q,\mathbb {P}^n_{\Bbbk }}$
:

For
![]() $S:=y_1G_1+\cdots +y_kG_k$
as before, define
$S:=y_1G_1+\cdots +y_kG_k$
as before, define
by the formal identity
which converges because we can rewrite
 $$ \begin{align*} \Psi_{q,S}&=\Psi_{q,\mathbb{P}^n_{\Bbbk}}\circ\exp(\gamma S-\gamma\mathrm{Fr}(S))\\ &=\Psi_{q,\mathbb{P}^n_{\Bbbk}}\circ\left(\prod_{i=1}^k\exp\left(\gamma y_iG_i-\gamma y_i^qG_i^q\right)\exp\left(\gamma y_i^qG_i^q-\gamma y_i^q\mathrm{Fr}_xG_i\right)\right) \end{align*} $$
$$ \begin{align*} \Psi_{q,S}&=\Psi_{q,\mathbb{P}^n_{\Bbbk}}\circ\exp(\gamma S-\gamma\mathrm{Fr}(S))\\ &=\Psi_{q,\mathbb{P}^n_{\Bbbk}}\circ\left(\prod_{i=1}^k\exp\left(\gamma y_iG_i-\gamma y_i^qG_i^q\right)\exp\left(\gamma y_i^qG_i^q-\gamma y_i^q\mathrm{Fr}_xG_i\right)\right) \end{align*} $$
and the final expression converges. Hence,
![]() $\Psi _{q,S}$
is still a cochain map by the same reason as in §5.1. Now, we may compare
$\Psi _{q,S}$
is still a cochain map by the same reason as in §5.1. Now, we may compare
![]() $\psi $
and
$\psi $
and
![]() $\Psi _{q,S}$
via
$\Psi _{q,S}$
via
![]() $\rho _S$
.
$\rho _S$
.
Proposition 5.3. There is a commutative diagram

Proof. We will follow Katz’s trick in the proof of [Reference Katz19, Th. 2.15]. We may decompose
![]() $\psi =\psi _x\circ \psi _y$
as in the case of
$\psi =\psi _x\circ \psi _y$
as in the case of
![]() $\mathrm {Fr}=\mathrm {Fr}_y\circ \mathrm {Fr}_x$
. Hence, there is a diagram
$\mathrm {Fr}=\mathrm {Fr}_y\circ \mathrm {Fr}_x$
. Hence, there is a diagram

where in the second and the third rows, we set
![]() $\deg _cy_i=-qd_i$
. The bottom square is commutative because
$\deg _cy_i=-qd_i$
. The bottom square is commutative because
 $$ \begin{align*} &(\psi_x\circ\rho_{\mathrm{Fr}_xS})\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\psi_x\left(\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_xS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_xS^{|\beta|}}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_x^{-1}\left(\mathrm{Tr}_x\left(\frac{x^u}{x_{\alpha}^{q-1}}\right)\right)\frac{dx_{\alpha}}{\hbar^{|\alpha|}q^{|\alpha|}}\wedge\frac{y^v}{\gamma^{|v|}S^{|v|}}\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\\&\quad =\rho_S\left(\mathrm{Fr}_x^{-1}\left(\mathrm{Tr}_x\left(\frac{x^u}{x_{\alpha}^{q-1}}\right)\right)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge y^vdy_{\beta}\right)\\&\quad =\rho_S\left(\frac{1}{x_{\alpha}}\mathrm{Fr}_x^{-1}\left(\mathrm{Tr}_x(x_{\alpha} x^u)\right)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge y^vdy_{\beta}\right)\\&\quad =\rho_S\left(\frac{q^{n+1}}{x_{\alpha}}\Psi_q(x_{\alpha} x^u)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge y^vdy_{\beta}\right)\\&\quad =\left(\rho_S\circ\Psi_{q,\mathbb{P}^n_{\Bbbk}}^x\right)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right). \end{align*} $$
$$ \begin{align*} &(\psi_x\circ\rho_{\mathrm{Fr}_xS})\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\psi_x\left(\frac{x^uy^v}{\gamma^{|v|}\mathrm{Fr}_xS^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}\mathrm{Fr}_xS^{|\beta|}}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_x^{-1}\left(\mathrm{Tr}_x\left(\frac{x^u}{x_{\alpha}^{q-1}}\right)\right)\frac{dx_{\alpha}}{\hbar^{|\alpha|}q^{|\alpha|}}\wedge\frac{y^v}{\gamma^{|v|}S^{|v|}}\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\\&\quad =\rho_S\left(\mathrm{Fr}_x^{-1}\left(\mathrm{Tr}_x\left(\frac{x^u}{x_{\alpha}^{q-1}}\right)\right)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge y^vdy_{\beta}\right)\\&\quad =\rho_S\left(\frac{1}{x_{\alpha}}\mathrm{Fr}_x^{-1}\left(\mathrm{Tr}_x(x_{\alpha} x^u)\right)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge y^vdy_{\beta}\right)\\&\quad =\rho_S\left(\frac{q^{n+1}}{x_{\alpha}}\Psi_q(x_{\alpha} x^u)\frac{dx_{\alpha}}{q^{|\alpha|}}\wedge y^vdy_{\beta}\right)\\&\quad =\left(\rho_S\circ\Psi_{q,\mathbb{P}^n_{\Bbbk}}^x\right)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right). \end{align*} $$
The middle square is commutative by Lemma 5.1. For the top square, we first compute
 $$ \begin{align*} &(\psi_y\circ\rho_S)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\psi_y\left(\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_y^{-1}\left(\mathrm{Tr}_y\left(\frac{y^v}{y_{\beta}^{q-1}\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{1}{y_{\beta}}\mathrm{Fr}_y^{-1}\left(\mathrm{Tr}_y\left(\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{q^k}{y_{\beta}}\Psi_q^y\left(\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}. \end{align*} $$
$$ \begin{align*} &(\psi_y\circ\rho_S)\left(x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\psi_y\left(\frac{x^uy^v}{\gamma^{|v|}S^{|v|}}\frac{dx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}\gamma^{|\beta|}S^{|\beta|}}\right)\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\mathrm{Fr}_y^{-1}\left(\mathrm{Tr}_y\left(\frac{y^v}{y_{\beta}^{q-1}\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{1}{y_{\beta}}\mathrm{Fr}_y^{-1}\left(\mathrm{Tr}_y\left(\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}\\&\quad =(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{q^k}{y_{\beta}}\Psi_q^y\left(\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}. \end{align*} $$
If we write
 $$ \begin{align*} \exp(\gamma t-\gamma t^q)=\sum_{m\geq0}b_mt^m, \end{align*} $$
$$ \begin{align*} \exp(\gamma t-\gamma t^q)=\sum_{m\geq0}b_mt^m, \end{align*} $$
then, denoting
![]() $e_{\beta }:=e_{\beta _1}+\cdots +e_{\beta _j}$
where
$e_{\beta }:=e_{\beta _1}+\cdots +e_{\beta _j}$
where
![]() $j=|\beta |$
and
$j=|\beta |$
and
![]() $e_{\beta _i}$
is the
$e_{\beta _i}$
is the
![]() $\beta _i$
th standard basis for
$\beta _i$
th standard basis for
![]() $\mathbb {Z}^{\oplus k}$
,
$\mathbb {Z}^{\oplus k}$
,
 $$ \begin{align*} &\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\Psi_{q,\mathbb{P}^n_{\Bbbk}}^y\left(\exp(\gamma S-\gamma\mathrm{Fr}_y\mathrm{Fr}_GS)x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\right)\\&\quad=\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\Psi_{q,\mathbb{P}^n_{\Bbbk}}^y\left(\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_m(yG)^mx^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\right)\\&\quad=\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\frac{q^k}{y_{\beta}}\Psi_q^y\left(\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_m(yG)^my_{\beta} y^v\right)x^udx_{\alpha}\wedge\frac{dy_{\beta}}{q^{|\beta|}}\right)\\&\quad=\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\frac{q^k}{y_{\beta}}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}y^mG^{qm-v-e_{\beta}}x^udx_{\alpha}\wedge\frac{dy_{\beta}}{q^{|\beta|}}\right)\\&\quad=\frac{q^k}{y_{\beta}}\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}(-1)^{|m|-1}(|m|-1)!\frac{y^mG^{qm-v-e_{\beta}}}{\gamma^{|m|}\mathrm{Fr}_GS^{|m|}}\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}. \end{align*} $$
$$ \begin{align*} &\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\Psi_{q,\mathbb{P}^n_{\Bbbk}}^y\left(\exp(\gamma S-\gamma\mathrm{Fr}_y\mathrm{Fr}_GS)x^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\right)\\&\quad=\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\Psi_{q,\mathbb{P}^n_{\Bbbk}}^y\left(\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_m(yG)^mx^uy^vdx_{\alpha}\wedge dy_{\beta}\right)\right)\\&\quad=\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\frac{q^k}{y_{\beta}}\Psi_q^y\left(\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_m(yG)^my_{\beta} y^v\right)x^udx_{\alpha}\wedge\frac{dy_{\beta}}{q^{|\beta|}}\right)\\&\quad=\rho_{\mathrm{Fr}_GS}\left(\frac{1}{q}\frac{q^k}{y_{\beta}}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}y^mG^{qm-v-e_{\beta}}x^udx_{\alpha}\wedge\frac{dy_{\beta}}{q^{|\beta|}}\right)\\&\quad=\frac{q^k}{y_{\beta}}\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}(-1)^{|m|-1}(|m|-1)!\frac{y^mG^{qm-v-e_{\beta}}}{\gamma^{|m|}\mathrm{Fr}_GS^{|m|}}\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}. \end{align*} $$
Hence, the commutativity follows if we show that
 $$ \begin{align} \begin{aligned} &(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\Psi_q^y\left(\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}\\&\quad=\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}(-1)^{|m|-1}(|m|-1)!\frac{y^mG^{qm-v-e_{\beta}}}{\gamma^{|m|}\mathrm{Fr}_GS^{|m|}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &(-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\Psi_q^y\left(\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)\frac{x^udx_{\alpha}}{\hbar^{|\alpha|}}\wedge\frac{dy_{\beta}}{\hbar^{|\beta|}q^{|\beta|}}\\&\quad=\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}(-1)^{|m|-1}(|m|-1)!\frac{y^mG^{qm-v-e_{\beta}}}{\gamma^{|m|}\mathrm{Fr}_GS^{|m|}}. \end{aligned} \end{align} $$
For this, consider the space of power series in t with the “usual” growth condition
 $$ \begin{align*} L:=\left\{f=\sum_{m\geq0}f_mt^m\ \middle|\ \begin{array}{c} f_m\in\Bbbk[x,y] \\\mathrm{val}_p(f_m)\geq bm+c \end{array}\right\} \end{align*} $$
$$ \begin{align*} L:=\left\{f=\sum_{m\geq0}f_mt^m\ \middle|\ \begin{array}{c} f_m\in\Bbbk[x,y] \\\mathrm{val}_p(f_m)\geq bm+c \end{array}\right\} \end{align*} $$
for some fixed
![]() $b>0$
and
$b>0$
and
![]() $c\in \mathbb {R}$
, depending on each f, and denote
$c\in \mathbb {R}$
, depending on each f, and denote
![]() $L^0:=tL$
. Define
$L^0:=tL$
. Define
in the usual way so that
Now, define for
![]() $f,g\in \Bbbk [x,y],$
$f,g\in \Bbbk [x,y],$
so that there is a commutative diagram

where each
![]() $(L^0,D_f)$
is regarded as a two term complex. On
$(L^0,D_f)$
is regarded as a two term complex. On
![]() $L^0/D_fL^0$
, we have
$L^0/D_fL^0$
, we have
At this point, we use the growth condition on
![]() $L^0$
. The differential equation
$L^0$
. The differential equation
with the condition
![]() $P\in t\Bbbk [x,y][[t]]$
has a unique power series solution
$P\in t\Bbbk [x,y][[t]]$
has a unique power series solution
 $$ \begin{align*} P=\frac{1-\exp(-\gamma f)}{\gamma f}. \end{align*} $$
$$ \begin{align*} P=\frac{1-\exp(-\gamma f)}{\gamma f}. \end{align*} $$
However, this does not belong to
![]() $L^0$
by the growth condition. Hence,
$L^0$
by the growth condition. Hence,
![]() $t\neq 0$
in
$t\neq 0$
in
![]() $L^0/D_fL^0$
so it is a free
$L^0/D_fL^0$
so it is a free
![]() $\Bbbk [x,y]$
-module of rank
$\Bbbk [x,y]$
-module of rank
![]() $1$
with basis
$1$
with basis
![]() $\{t\}$
. For
$\{t\}$
. For
![]() $\xi \in \Bbbk [x,y]$
,
$\xi \in \Bbbk [x,y]$
,
 $$ \begin{align*} \Psi_{q,f}^{y,t}(\xi)&=\Psi_q^{y,t}\left(\sum_{m\geq0}\frac{\gamma^m}{m!}(ft-f(x,y^q)\cdot t^q)^m\xi\right)\\&=\Psi_q^{y,t}\left(\sum_{m\geq0}\sum_{\ell=0}^m\binom{m}{\ell}(-1)^{m-\ell}(f(x,y^q)t^q)^{m-\ell}(ft)^{\ell}\xi\right)\\&=\sum_{m\geq0}\sum_{\ell=0}^m\binom{m}{\ell}(-1)^{m-\ell}(ft)^{m-\ell}\Psi_q^{y,t}\left((ft)^{\ell}\xi\right)\\&\equiv\Psi_q^y(\xi)\bmod t \end{align*} $$
$$ \begin{align*} \Psi_{q,f}^{y,t}(\xi)&=\Psi_q^{y,t}\left(\sum_{m\geq0}\frac{\gamma^m}{m!}(ft-f(x,y^q)\cdot t^q)^m\xi\right)\\&=\Psi_q^{y,t}\left(\sum_{m\geq0}\sum_{\ell=0}^m\binom{m}{\ell}(-1)^{m-\ell}(f(x,y^q)t^q)^{m-\ell}(ft)^{\ell}\xi\right)\\&=\sum_{m\geq0}\sum_{\ell=0}^m\binom{m}{\ell}(-1)^{m-\ell}(ft)^{m-\ell}\Psi_q^{y,t}\left((ft)^{\ell}\xi\right)\\&\equiv\Psi_q^y(\xi)\bmod t \end{align*} $$
so we deduce that
for some
![]() $\omega \in L^0$
. Hence,
$\omega \in L^0$
. Hence,
![]() $\Psi _{q,f}^{y,t}$
on
$\Psi _{q,f}^{y,t}$
on
![]() $L^0/D_fL^0$
is merely
$L^0/D_fL^0$
is merely
Therefore,
 $$ \begin{align*} &\Psi_q^y\left((-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)t\\&\quad=\frac{1}{q}\Psi_{q,S}^{y,t}\left((-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}t\right)\\&\quad=\frac{1}{q}\Psi_{q,S,\mathrm{Fr}_GS}^{y,t}\left(y_{\beta} y^vt^{|v|+|\beta|}\right)\\&\quad=\frac{1}{q}\Psi_q^{y,t}\left(\exp(\gamma St-\gamma\mathrm{Fr}_y\mathrm{Fr}_GSt^q)y_{\beta} y^vt^{|v|+|\beta|}\right)\\&\quad=\frac{1}{q}\Psi_q^{y,t}\left(\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_m(yG)^my_{\beta} y^vt^{|m|+|v|+|\beta|}\right)\\&\quad=\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}y^mG^{m-v-e_{\beta}}t^{|m|}\\&\quad=\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}(-1)^{|m|-1}(|m|-1)!\frac{y^mG^{m-v-e_{\beta}}}{\gamma^{|m|}\mathrm{Fr}_GS^{|m|}}t, \end{align*} $$
$$ \begin{align*} &\Psi_q^y\left((-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}\right)t\\&\quad=\frac{1}{q}\Psi_{q,S}^{y,t}\left((-1)^{|v|+|\beta|-1}(|v|+|\beta|-1)!\frac{y_{\beta} y^v}{\gamma^{|v|+|\beta|}S^{|v|+|\beta|}}t\right)\\&\quad=\frac{1}{q}\Psi_{q,S,\mathrm{Fr}_GS}^{y,t}\left(y_{\beta} y^vt^{|v|+|\beta|}\right)\\&\quad=\frac{1}{q}\Psi_q^{y,t}\left(\exp(\gamma St-\gamma\mathrm{Fr}_y\mathrm{Fr}_GSt^q)y_{\beta} y^vt^{|v|+|\beta|}\right)\\&\quad=\frac{1}{q}\Psi_q^{y,t}\left(\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_m(yG)^my_{\beta} y^vt^{|m|+|v|+|\beta|}\right)\\&\quad=\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}y^mG^{m-v-e_{\beta}}t^{|m|}\\&\quad=\frac{1}{q}\sum_{m\in\mathbb{Z}_{\geq0}^{\oplus k}}b_{qm-v-e_{\beta}}(-1)^{|m|-1}(|m|-1)!\frac{y^mG^{m-v-e_{\beta}}}{\gamma^{|m|}\mathrm{Fr}_GS^{|m|}}t, \end{align*} $$
that is, (5.2) holds, and the proof is completed.
§A Remarks on algebraic de Rham cohomology
Definition A.1. Given a map of schemes
![]() $X\rightarrow S$
, define its (relative) de Rham cohomology to be
$X\rightarrow S$
, define its (relative) de Rham cohomology to be
where
![]() $\Omega _{X/S}^{\bullet }$
is the algebraic de Rham complex.
$\Omega _{X/S}^{\bullet }$
is the algebraic de Rham complex.
Lemma A.2. Given a map of affine schemes
![]() $X\rightarrow S$
, if
$X\rightarrow S$
, if
![]() $A=\Gamma (S,\mathcal {O}_S)$
,
$A=\Gamma (S,\mathcal {O}_S)$
,
![]() $X=\Gamma (X,\mathcal {O}_X)$
, and
$X=\Gamma (X,\mathcal {O}_X)$
, and
![]() $A\rightarrow B$
the corresponding ring map, then
$A\rightarrow B$
the corresponding ring map, then
in
![]() $\mathrm {D}(A)$
, the derived category of A. Consequently,
$\mathrm {D}(A)$
, the derived category of A. Consequently,
where d is the usual de Rham differential.
Proof. Since
![]() $\Omega _{X/S}^p$
is quasicoherent
$\Omega _{X/S}^p$
is quasicoherent
![]() $\mathcal {O}_X$
-module and X is affine,
$\mathcal {O}_X$
-module and X is affine,
 $$ \begin{align*} H^q(X,\Omega_{X/S}^p)=\left\{\begin{array}{ll} \Gamma(X,\Omega_{X/S}^p), & \textrm{if}\quad q=0,\\ 0, & \textrm{if}\quad q>0. \end{array} \right. \end{align*} $$
$$ \begin{align*} H^q(X,\Omega_{X/S}^p)=\left\{\begin{array}{ll} \Gamma(X,\Omega_{X/S}^p), & \textrm{if}\quad q=0,\\ 0, & \textrm{if}\quad q>0. \end{array} \right. \end{align*} $$
In other words,
![]() $\Omega _{X/S}^{\bullet }$
is a bounded below complex of
$\Omega _{X/S}^{\bullet }$
is a bounded below complex of
![]() $\Gamma (X,-)$
-acyclic objects so the canonical map
$\Gamma (X,-)$
-acyclic objects so the canonical map
is an isomorphism.
Remark A.3. To show the second assertion of Lemma A.2, one may argue with the Čech spectral sequence for a chosen covering
![]() $\mathcal {U}$
of X:
$\mathcal {U}$
of X:
where
![]() $\underline {H}^q(\Omega _{X/S}^{\bullet })$
is the presheaf associate with U, a complex of abelian groups
$\underline {H}^q(\Omega _{X/S}^{\bullet })$
is the presheaf associate with U, a complex of abelian groups
and
![]() $\mathrm {Tot}$
takes the total complex of a double complex. For this, one may even use the covering
$\mathrm {Tot}$
takes the total complex of a double complex. For this, one may even use the covering
![]() $\{\mathrm {Id}_X:X\rightarrow X\}$
to get the desired vanishing because X is affine.
$\{\mathrm {Id}_X:X\rightarrow X\}$
to get the desired vanishing because X is affine.
In computing algebraic de Rham cohomology of affine schemes, one may rely on cosimplicial de Rham algebras. For this, we introduce some terminologies on (co-)simplicial objects. Let
![]() $\Delta $
be the simplex category and
$\Delta $
be the simplex category and
![]() $\mathscr {C}$
a finitely bicomplete category, that is,
$\mathscr {C}$
a finitely bicomplete category, that is,
![]() $\mathscr {C}$
has finite limits and finite colimits. For
$\mathscr {C}$
has finite limits and finite colimits. For
![]() $n\in \mathbb {N}$
, denote
$n\in \mathbb {N}$
, denote
![]() $\Delta _{\leq n}$
the full subcategory of
$\Delta _{\leq n}$
the full subcategory of
![]() $\Delta $
consisting of
$\Delta $
consisting of
![]() $[0],\ldots ,[n]$
and the obvious inclusion
$[0],\ldots ,[n]$
and the obvious inclusion
Since
![]() $\mathscr {C}$
has finite limits and finite colimits, there are adjoint pairs
$\mathscr {C}$
has finite limits and finite colimits, there are adjoint pairs

given as in [Reference Artin, Grothendieck and Verdier6, V. 7.1]. Using these, we introduce the following terminologies.
Definition A.4. Let
![]() $\Delta $
be the simplex category.
$\Delta $
be the simplex category.
(1) The nth truncation is
(2) The nth skeleton is
(3) The nth coskeleton is
A simplicial object X in
![]() $\mathscr {C}$
is said to be n-skeletal (resp. n-coskeletal) if X is isomorphic to its nth skeleton (resp. nth coskeleton).
$\mathscr {C}$
is said to be n-skeletal (resp. n-coskeletal) if X is isomorphic to its nth skeleton (resp. nth coskeleton).
In our context, we will only work with
![]() $0$
-coskeletal simplicial objects. Namely, given a map of schemes
$0$
-coskeletal simplicial objects. Namely, given a map of schemes
![]() $X\rightarrow S$
, that is, an object in
$X\rightarrow S$
, that is, an object in
![]() $\mathrm {Sch}_{/S}$
, the category of S-schemes, we may regard it as a constant simplicial object in
$\mathrm {Sch}_{/S}$
, the category of S-schemes, we may regard it as a constant simplicial object in
![]() $\mathrm {Sch}_{/S}$
. Since
$\mathrm {Sch}_{/S}$
. Since
![]() $\mathrm {Sch}_{/S}$
has finite limits, we may take its
$\mathrm {Sch}_{/S}$
has finite limits, we may take its
![]() $0$
th coskeleton, which will be given by
$0$
th coskeleton, which will be given by
where the ith boundary map forgets ith factor and the ith degeneracy map duplicates the ith factor, counted from
![]() $0$
. When
$0$
. When
![]() $X\rightarrow S$
is a map of affine schemes corresponding to a ring map
$X\rightarrow S$
is a map of affine schemes corresponding to a ring map
![]() $A\rightarrow B$
, the above simplicial object defines a cosimplicial A-algebra:
$A\rightarrow B$
, the above simplicial object defines a cosimplicial A-algebra:
If, furthermore,
![]() $A\rightarrow B$
is a
$A\rightarrow B$
is a
![]() $\Bbbk $
-algebra map over a ground ring
$\Bbbk $
-algebra map over a ground ring
![]() $\Bbbk $
, then we may take the de Rham complex degreewisely to get a cosimplicial de Rham algebra:
$\Bbbk $
, then we may take the de Rham complex degreewisely to get a cosimplicial de Rham algebra:
Lemma A.5. If
![]() $A\rightarrow B$
is an étale
$A\rightarrow B$
is an étale
![]() $\Bbbk $
-algebra map, then the associated cosimplicial de Rham algebra
$\Bbbk $
-algebra map, then the associated cosimplicial de Rham algebra
![]() $\Omega _{(B/A)^{\bullet }/\Bbbk }^{\bullet }$
is
$\Omega _{(B/A)^{\bullet }/\Bbbk }^{\bullet }$
is
![]() $0$
-coskeletal (in the opposite category).
$0$
-coskeletal (in the opposite category).
Proof. Recall that for
![]() $n\geq 0$
,
$n\geq 0$
,
so
![]() $A\rightarrow (B/A)^n$
remains étale for every
$A\rightarrow (B/A)^n$
remains étale for every
![]() $n\geq 0$
. Hence, the exact sequence
$n\geq 0$
. Hence, the exact sequence
together with
![]() $\Omega _{(B/A)^n/A}^1=0$
shows that
$\Omega _{(B/A)^n/A}^1=0$
shows that
This, together with the flatness of
![]() $A\rightarrow (B/A)^n$
, gives
$A\rightarrow (B/A)^n$
, gives
so the assertion follows.
Proposition A.6. Let
![]() $\Bbbk $
be a ring. If
$\Bbbk $
be a ring. If
![]() $A\rightarrow B$
is a faithfully flat étale
$A\rightarrow B$
is a faithfully flat étale
![]() $\Bbbk $
-algebra, then
$\Bbbk $
-algebra, then
is a
![]() $0$
-coskeletal cosimplicial resolution.
$0$
-coskeletal cosimplicial resolution.
Proof. Being a
![]() $0$
-coskeletal object follows immediately from Lemma A.5. Being a cosimplicial resolution means that the given map induces a quasi-isomorphism of cochain complexes:
$0$
-coskeletal object follows immediately from Lemma A.5. Being a cosimplicial resolution means that the given map induces a quasi-isomorphism of cochain complexes:
where
![]() $C^{\bullet }$
takes the unnormalized complex (see, e.g., [Reference Weibel33, Def. 8.2.1]) in the cosimplicial direction, and
$C^{\bullet }$
takes the unnormalized complex (see, e.g., [Reference Weibel33, Def. 8.2.1]) in the cosimplicial direction, and
![]() $\mathrm {Tot}$
takes its total complex. In fact, the total complex will be a Čech–de Rham complex of
$\mathrm {Tot}$
takes its total complex. In fact, the total complex will be a Čech–de Rham complex of
![]() $\Omega _{A/\Bbbk }^{\bullet }$
with respect to the covering
$\Omega _{A/\Bbbk }^{\bullet }$
with respect to the covering
![]() $\{\operatorname {\mathrm {Spec}} B\rightarrow \operatorname {\mathrm {Spec}} A\}$
which is surjective as
$\{\operatorname {\mathrm {Spec}} B\rightarrow \operatorname {\mathrm {Spec}} A\}$
which is surjective as
![]() $A\rightarrow B$
is faithfully flat. Therefore, the total complex computes the algebraic de Rham cohomology of A over
$A\rightarrow B$
is faithfully flat. Therefore, the total complex computes the algebraic de Rham cohomology of A over
![]() $\Bbbk $
, and the above map becomes the augmentation map.
$\Bbbk $
, and the above map becomes the augmentation map.
Example A.7. Given an affine scheme X and a finite affine open covering
![]() $\{U_i\}_{i\in I}$
of X, the induced map
$\{U_i\}_{i\in I}$
of X, the induced map

is a faithfully flat étale map of affine schemes. Here, the finiteness of I is necessary for the coproduct to be affine. Then the total complex induced from the cosimplicial de Rham algebra
![]() $\Omega _{(U/X)_{\bullet }/\Bbbk }^{\bullet }$
will be the Čech–de Rham complex with respect to the Zariski cover
$\Omega _{(U/X)_{\bullet }/\Bbbk }^{\bullet }$
will be the Čech–de Rham complex with respect to the Zariski cover
![]() $\{U_i\}_{i\in I}$
of X. However, being
$\{U_i\}_{i\in I}$
of X. However, being
![]() $0$
-coskeletal cosimplicial objects, maps of such de Rham algebras are determined at the level of
$0$
-coskeletal cosimplicial objects, maps of such de Rham algebras are determined at the level of
![]() $0$
th truncation:
$0$
th truncation:
 $$ \begin{align*} \prod_{i\in I}\Omega_{U_i/\Bbbk}^{\bullet}. \end{align*} $$
$$ \begin{align*} \prod_{i\in I}\Omega_{U_i/\Bbbk}^{\bullet}. \end{align*} $$
Acknowledgment
I thank my advisor Jeehoon Park for his encouragement of this project. I also thank Dohyeong Kim and Wansu Kim for helpful discussions.
Funding
Junyeong Park was supported by Samsung Science and Technology Foundation under Project Number SSTF-BA2001-02.