Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T03:58:57.208Z Has data issue: false hasContentIssue false
  • English
  • Français

On Meromorphic Mappings into Taut Complex Analytic Spaces

Published online by Cambridge University Press:  22 January 2016

Toshio Urata
Toshio Urata*
Affiliation:
Aichi University of Education
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study a certain difference between meromorphic mappings and holomorphic mappings into taut complex analytic spaces. We prove in §2 that, for any complex analytic space X, there exists a unique proper modification 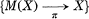of X with center Sg (X) which is minimal with respect to the property that M(X) is normal and, for any T-meromorphic mapping f: X → Y (see Definition 1.3) into a complex analytic space Y, there exists a unique holomorphic mapping 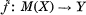such that 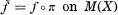except some nowhere dense complex analytic set, where Sg(X) denotes the set of all singular points of X.

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 50 , June 1973 , pp. 49 - 65
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Barth, T. J.: Taut and tight complex manifolds, Proc. Amer. Math. Soc, 24 (1970), 429–431.Google Scholar
[2] Cartan, H.: Quotients of complex analytic spaces, In Contributions of Function Theory, Tata Institute, Bombay, (1960), 1–15.Google Scholar
[3] Fujimoto, H.: On holomorphic mappings into a taut complex space, Nagoya Math. J., 46 (1971), 49–61.Google Scholar
[4] Grauert, H. und Kerner, H.: Deformationen von Singularitaten komplexer Raume, Math. Ann., 153 (1964), 236–260.Google Scholar
[5] Hironaka, H.: Resolution of singularities of an algebraic variety over a field of characteristic zero, Ann. of Math., 79 (1964), 109–326.Google Scholar
[6] Holman, H.: Local properties of holomorphic mappings, Proc. Conf. on Complex Analysis, Mineapolis (1964), 94–109.Google Scholar
[7] Kaup, W.: Hyperbolische komplexe Raume, Ann. Inst. Fourier (Grenoble), 18 (1968), 303–330.Google Scholar
[8] Kaup, W.: Reele Transformationsgruppe und invariante Metriken auf komplexen Raumen, Inventiones math., 3 (1970), 43–70.Google Scholar
[9] Kiernan, P. J.: On the relation between taut, tight and hyperbolic manifolds, Bull. Am. Math. Soc, 76 (1967), 49–51.CrossRefGoogle Scholar
[10] Kobayashi, S.: Invariant distances on complex manifolds and holomorphic mappings, J. Math. Soc. Japan, 19 (1967), 460–480.Google Scholar
[11] Kobayashi, S.: Hperbolic manifolds and holomorphic mappings, Marcel Dekker, Inc., New York, 1970.Google Scholar
[12] Kwack, M. H.: Generalization of the big Picard theorem, Ann. Math., 90 (1969), 13–22.CrossRefGoogle Scholar
[13] Wagreich, P.: Elliptic singularities of surfaces, Amer. J. Math., 92 (1970), 419–454.CrossRefGoogle Scholar
[14] Wu, H.: Normal family of holomorphic mappings, Acta Math., 119 (1967), 194–329.CrossRefGoogle Scholar