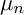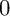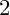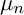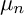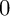1 Introduction
K3 surfaces are proper smooth surfaces X with
![]() $\Omega ^2_X \cong \mathcal {O}_X$
and
$\Omega ^2_X \cong \mathcal {O}_X$
and
![]() $H^1(X, \mathcal {O}_X) = 0$
. The first condition implies that X admits an everywhere nonvanishing
$H^1(X, \mathcal {O}_X) = 0$
. The first condition implies that X admits an everywhere nonvanishing
![]() $2$
-form, and such a
$2$
-form, and such a
![]() $2$
-form is unique up to scalar. An automorphism of a K3 surface is called symplectic if it preserves the global
$2$
-form is unique up to scalar. An automorphism of a K3 surface is called symplectic if it preserves the global
![]() $2$
-form. It is known that symplectic and non-symplectic automorphisms behave very differently.
$2$
-form. It is known that symplectic and non-symplectic automorphisms behave very differently.
For example, Nikulin [Reference MukaiNi, §§4 and 5] proved that quotients of K3 surfaces in characteristic
![]() $0$
by a symplectic action of a finite group G has only rational double points (RDPs) as singularities and that the minimal resolutions of the quotients are again K3 surfaces. Moreover, he determined the number of fixed points (which are always isolated) if G is cyclic. To the contrary, the quotients by non-symplectic actions of finite groups are never birational to K3 surfaces; instead, they are birational to either Enriques surfaces or rational surfaces.
$0$
by a symplectic action of a finite group G has only rational double points (RDPs) as singularities and that the minimal resolutions of the quotients are again K3 surfaces. Moreover, he determined the number of fixed points (which are always isolated) if G is cyclic. To the contrary, the quotients by non-symplectic actions of finite groups are never birational to K3 surfaces; instead, they are birational to either Enriques surfaces or rational surfaces.
These results hold in characteristic
![]() $p> 0$
provided p does not divide the order of G (see Theorem 5.1), but are no longer true for order p automorphisms in characteristic p. In this case, the notion of symplecticness is useless, since any such automorphism is automatically symplectic (since there are no nontrivial pth root of unity in characteristic p) and, for small p, there exist examples of automorphisms with non-K3 quotients (see [Reference Dolgachev and KeumDK1], [Reference Dolgachev and KeumDK2]).
$p> 0$
provided p does not divide the order of G (see Theorem 5.1), but are no longer true for order p automorphisms in characteristic p. In this case, the notion of symplecticness is useless, since any such automorphism is automatically symplectic (since there are no nontrivial pth root of unity in characteristic p) and, for small p, there exist examples of automorphisms with non-K3 quotients (see [Reference Dolgachev and KeumDK1], [Reference Dolgachev and KeumDK2]).
In this paper, we consider actions of the finite group schemes
![]() $\mu _{n}$
(n may be divisible by p) on RDP K3 surfaces, by which we mean surfaces with RDP singularities whose minimal resolutions are K3 surfaces. It is essential to allow RDPs since smooth K3 surfaces never admit actions of
$\mu _{n}$
(n may be divisible by p) on RDP K3 surfaces, by which we mean surfaces with RDP singularities whose minimal resolutions are K3 surfaces. It is essential to allow RDPs since smooth K3 surfaces never admit actions of
![]() $\mu _p$
(see Remark 2.2). We introduce the notion of symplecticness and fixed points of such actions (Definitions 2.5 and 2.7). Then we prove the following properties, which are parallel to the properties of automorphisms of order not divisible by the characteristic.
$\mu _p$
(see Remark 2.2). We introduce the notion of symplecticness and fixed points of such actions (Definitions 2.5 and 2.7). Then we prove the following properties, which are parallel to the properties of automorphisms of order not divisible by the characteristic.
Theorem 1.1 (Theorems 6.1 and 6.2)
Let X be an RDP K3 surface in characteristic p, equipped with a
![]() $\mu _{n}$
-action. If the action is symplectic, then the quotient
$\mu _{n}$
-action. If the action is symplectic, then the quotient
![]() $X/\mu _{n}$
is an RDP K3 surface. If
$X/\mu _{n}$
is an RDP K3 surface. If
![]() $n = p$
and the action is non-symplectic, then the quotient
$n = p$
and the action is non-symplectic, then the quotient
![]() $X/\mu _{p}$
is an RDP Enriques surface if the action is fixed-point-free (which is possible only if
$X/\mu _{p}$
is an RDP Enriques surface if the action is fixed-point-free (which is possible only if
![]() $p = 2$
), and otherwise it is a rational surface.
$p = 2$
), and otherwise it is a rational surface.
Theorem 1.2 (Theorems 7.1 and 8.2)
-
• There exists an RDP K3 surface X in characteristic p equipped with a
 $\mu _{p}$
-action if and only if
$\mu _{p}$
-action if and only if
 $p \leq 19$
.
$p \leq 19$
. -
• If X is an RDP K3 surface X in characteristic p equipped with a
 $\mu _{n}$
-action, then
$\mu _{n}$
-action, then
 $\phi (n) \leq 20$
, in particular
$\phi (n) \leq 20$
, in particular
 $n \leq 66$
. Moreover, for each p, we determine the set of n for which such an action exists.
$n \leq 66$
. Moreover, for each p, we determine the set of n for which such an action exists. -
• For each p, there exists an RDP K3 surface X in characteristic p equipped with a symplectic
 $\mu _{n}$
-action if and only if
$\mu _{n}$
-action if and only if
 $n \leq 8$
, and we determine the number of fixed points.
$n \leq 8$
, and we determine the number of fixed points.
To prove the main results, we first study (in §§3 and 4)
![]() $\mu _n$
-actions on local rings of surfaces at smooth points and RDPs. We define the notion of symplecticness of such actions (Definitions 3.1 and 4.1) and prove the following result.
$\mu _n$
-actions on local rings of surfaces at smooth points and RDPs. We define the notion of symplecticness of such actions (Definitions 3.1 and 4.1) and prove the following result.
Theorem 1.3 (Theorem 4.6 and Propositions 4.7 and 4.9)
Let X be the localization at a closed point w of an RDP surface in characteristic p equipped with a
![]() $\mu _{p}$
-action. Let
$\mu _{p}$
-action. Let
![]() ${\pi } : {X}\to {X/\mu _p}$
be the quotient morphism.
${\pi } : {X}\to {X/\mu _p}$
be the quotient morphism.
-
• If w is not fixed by the action, then
 $\pi (w)$
is either a smooth point or an RDP.
$\pi (w)$
is either a smooth point or an RDP. -
• If w is fixed and the action is symplectic at w, then w is an isolated fixed point and
 $\pi (w)$
is an RDP.
$\pi (w)$
is an RDP. -
• If w is an isolated fixed point and the action is non-symplectic at w, then
 $\pi (w)$
is a non-RDP singularity.
$\pi (w)$
is a non-RDP singularity.
We classify the possible actions in the non-fixed case (Table 3) and the symplectic case (Table 4).
Moreover, we also give a partial classification of local
![]() $\mu _{p^e}$
- and
$\mu _{p^e}$
- and
![]() $\mu _n$
-actions (Propositions 4.12 and 4.13) and a complete classification of local symplectic
$\mu _n$
-actions (Propositions 4.12 and 4.13) and a complete classification of local symplectic
![]() $\mu _n$
-actions (Proposition 4.14). We hope that these local results would have applications other than K3 surfaces.
$\mu _n$
-actions (Proposition 4.14). We hope that these local results would have applications other than K3 surfaces.
The results on
![]() $\mu _n$
-quotients, orders of symplectic
$\mu _n$
-quotients, orders of symplectic
![]() $\mu _n$
-actions, and orders of
$\mu _n$
-actions, and orders of
![]() $\mu _n$
-actions on K3 surfaces are discussed in §§6–8, respectively.
$\mu _n$
-actions on K3 surfaces are discussed in §§6–8, respectively.
In §9, we give several examples of
![]() $\mu _{n}$
-actions on K3 surfaces.
$\mu _{n}$
-actions on K3 surfaces.
Throughout the paper, we work over an algebraically closed field k of
![]() $\operatorname {\mathrm {char}} k = p \geq 0$
. Varieties are separated integral k-schemes of finite type (not necessarily proper or smooth), and surfaces are two-dimensional varieties. We denote the smooth locus of a variety X by
$\operatorname {\mathrm {char}} k = p \geq 0$
. Varieties are separated integral k-schemes of finite type (not necessarily proper or smooth), and surfaces are two-dimensional varieties. We denote the smooth locus of a variety X by
![]() $X^{\mathrm {sm}}$
.
$X^{\mathrm {sm}}$
.
2 Preliminaries
2.1 K3 surfaces and rational double points
RDP singularities of surfaces are precisely the canonical surface singularities that are not smooth. They are classified into types
![]() $A_n$
(
$A_n$
(
![]() $n \geq 1$
),
$n \geq 1$
),
![]() $D_n$
(
$D_n$
(
![]() $n \geq 4$
), and
$n \geq 4$
), and
![]() $E_n$
(
$E_n$
(
![]() $n = 6,7,8$
) by their dual graph of the exceptional curves of the minimal resolution, which are Dynkin diagrams of type
$n = 6,7,8$
) by their dual graph of the exceptional curves of the minimal resolution, which are Dynkin diagrams of type
![]() $A_n$
,
$A_n$
,
![]() $D_n$
, or
$D_n$
, or
![]() $E_n$
. The number n is equal to the number of the exceptional curves, and we say that the RDP is of index n. The dual graph determines the formal isomorphism class of an RDP except in certain cases in characteristics
$E_n$
. The number n is equal to the number of the exceptional curves, and we say that the RDP is of index n. The dual graph determines the formal isomorphism class of an RDP except in certain cases in characteristics
![]() $2,3,5$
. For the exceptional cases, we use Artin’s notation
$2,3,5$
. For the exceptional cases, we use Artin’s notation
![]() $D_n^r$
and
$D_n^r$
and
![]() $E_n^r$
(see [Reference ArtinA2]).
$E_n^r$
(see [Reference ArtinA2]).
We recall the classification, given by Bombieri and Mumford [Reference Bombieri and MumfordBM2], of proper smooth surfaces X with numerically trivial canonical divisor
![]() $K_X$
: they consist of four classes, with the characterizing properties as reported in Table 1. Here,
$K_X$
: they consist of four classes, with the characterizing properties as reported in Table 1. Here,
![]() $b_i = \dim H_{\mathrm {\acute et}}^i(X, \mathbb Q_l)$
is the ith l-adic Betti number for an auxiliary prime
$b_i = \dim H_{\mathrm {\acute et}}^i(X, \mathbb Q_l)$
is the ith l-adic Betti number for an auxiliary prime
![]() $l \neq \operatorname {\mathrm {char}} k$
. Enriques and (quasi-)hyperelliptic surfaces in characteristics
$l \neq \operatorname {\mathrm {char}} k$
. Enriques and (quasi-)hyperelliptic surfaces in characteristics
![]() $2$
and
$2$
and
![]() $3$
may have unusual values of
$3$
may have unusual values of
![]() $\dim H^1(\mathcal {O}_X)$
and
$\dim H^1(\mathcal {O}_X)$
and
![]() $\operatorname {\mathrm {ord}}(K_X)$
.
$\operatorname {\mathrm {ord}}(K_X)$
.
Table 1 Surfaces with numerically trivial canonical divisors.

The distinction between hyperelliptic and quasi-hyperelliptic surfaces is not important in this paper. Furthermore, the choice of the origin of an abelian surface is not important.
Definition 2.1. RDP surfaces are surfaces that have only RDPs as singularities (if any). Hence, any smooth surface is an RDP surface by definition.
RDP K3 surfaces are proper RDP surfaces whose minimal resolutions are (smooth) K3 surfaces. We similarly define RDP abelian, RDP Enriques, and RDP (quasi-)hyperelliptic surfaces.
However, since abelian surfaces and (quasi-)hyperelliptic surfaces do not admit smooth rational curves, any RDP abelian or RDP (quasi-)hyperelliptic surface is smooth.
Remark 2.2. Smooth K3 surfaces in characteristic
![]() $p> 0$
admit no nontrivial global vector fields ([Reference OgusRS, Th. 7], [Reference NikulinNy1, Cor. 3.5]), and hence admit no nontrivial actions of
$p> 0$
admit no nontrivial global vector fields ([Reference OgusRS, Th. 7], [Reference NikulinNy1, Cor. 3.5]), and hence admit no nontrivial actions of
![]() $\mu _p$
(or
$\mu _p$
(or
![]() $\alpha _p$
). However, RDP K3 surfaces may admit such actions.
$\alpha _p$
). However, RDP K3 surfaces may admit such actions.
Proposition 2.3. For any RDP surface X, the pullback by the morphism
![]() $X^{\mathrm {sm}} \cong \tilde X \setminus E \hookrightarrow \tilde X$
to the minimal resolution
$X^{\mathrm {sm}} \cong \tilde X \setminus E \hookrightarrow \tilde X$
to the minimal resolution
![]() $\tilde X$
of X induces an isomorphism
$\tilde X$
of X induces an isomorphism
![]() $H^0(X^{\mathrm {sm}}, (\Omega ^2_X)^{\otimes n}) \cong H^0(\tilde X, (\Omega ^2_{\tilde X})^{\otimes n})$
, where E is the exceptional divisor. Nonvanishing forms on one side correspond to nonvanishing ones on the other side.
$H^0(X^{\mathrm {sm}}, (\Omega ^2_X)^{\otimes n}) \cong H^0(\tilde X, (\Omega ^2_{\tilde X})^{\otimes n})$
, where E is the exceptional divisor. Nonvanishing forms on one side correspond to nonvanishing ones on the other side.
Proof. This follows from the following local version applied repeatedly.
Proposition 2.4. Let
![]() $(A,\mathfrak {m})$
be the localization at a closed point of an RDP surface. Then
$(A,\mathfrak {m})$
be the localization at a closed point of an RDP surface. Then
![]() $H^0(\operatorname {\mathrm {Spec}} A \setminus \{\mathfrak {m}\}, \Omega ^2_{A/k})$
is a free A-module of rank 1. If A is smooth, then this space is isomorphic to
$H^0(\operatorname {\mathrm {Spec}} A \setminus \{\mathfrak {m}\}, \Omega ^2_{A/k})$
is a free A-module of rank 1. If A is smooth, then this space is isomorphic to
![]() $H^0(\operatorname {\mathrm {Spec}} A, \Omega ^2_{A/k})$
. If A is an RDP and
$H^0(\operatorname {\mathrm {Spec}} A, \Omega ^2_{A/k})$
. If A is an RDP and
![]() $(A',\mathfrak {m}')$
is the localization at a closed point of
$(A',\mathfrak {m}')$
is the localization at a closed point of
![]() $\operatorname {\mathrm {Bl}}_{\mathfrak {m}} A$
, then any generator of the above space extends to a generator of
$\operatorname {\mathrm {Bl}}_{\mathfrak {m}} A$
, then any generator of the above space extends to a generator of
![]() $H^0(\operatorname {\mathrm {Spec}} A' \setminus \{\mathfrak {m}'\}, \Omega ^2_{A'/k})$
.
$H^0(\operatorname {\mathrm {Spec}} A' \setminus \{\mathfrak {m}'\}, \Omega ^2_{A'/k})$
.
Proof. If A is smooth, then
![]() $\Omega ^2_{A/k}$
is free of rank
$\Omega ^2_{A/k}$
is free of rank
![]() $1$
and the assertion is clear. Suppose A is an RDP. Then it is a hypersurface isolated singularity, and it is well known that for such singularities, the canonical divisor is trivial, and then the former assertion follows. Since an RDP is a canonical singularity, the pullback of the canonical divisor to
$1$
and the assertion is clear. Suppose A is an RDP. Then it is a hypersurface isolated singularity, and it is well known that for such singularities, the canonical divisor is trivial, and then the former assertion follows. Since an RDP is a canonical singularity, the pullback of the canonical divisor to
![]() $\operatorname {\mathrm {Bl}}_{\mathfrak {m}} A$
is also trivial, and hence the latter assertion follows.
$\operatorname {\mathrm {Bl}}_{\mathfrak {m}} A$
is also trivial, and hence the latter assertion follows.
2.2 Group schemes of multiplicative type
Recall that we are working over an algebraically closed field k.
We consider finite commutative group schemes G of multiplicative type over k. This means that G is of the form
![]() $\prod _j \mu _{n_j}$
for some positive integers
$\prod _j \mu _{n_j}$
for some positive integers
![]() $n_j$
. The Cartier dual
$n_j$
. The Cartier dual
![]() $G^{\vee } = \operatorname {\mathrm {\mathcal {H}\mathit {om}}}(G, \mathbb G_m)$
of G is a finite étale group scheme and can be identified with the finite group
$G^{\vee } = \operatorname {\mathrm {\mathcal {H}\mathit {om}}}(G, \mathbb G_m)$
of G is a finite étale group scheme and can be identified with the finite group
![]() $G^{\vee }(k)$
of k-valued points. Using this finite commutative group
$G^{\vee }(k)$
of k-valued points. Using this finite commutative group
![]() $G^{\vee }$
, we have the following explicit description:
$G^{\vee }$
, we have the following explicit description:
![]() $G = \operatorname {\mathrm {Spec}} k[t_{i}]_{i \in G^{\vee }} / (t_{i} t_{j} - t_{i+j}, t_0 - 1)$
, with the group operations
$G = \operatorname {\mathrm {Spec}} k[t_{i}]_{i \in G^{\vee }} / (t_{i} t_{j} - t_{i+j}, t_0 - 1)$
, with the group operations
![]() $m \colon G \times G \to G$
,
$m \colon G \times G \to G$
,
![]() $e \colon \operatorname {\mathrm {Spec}} k \to G$
,
$e \colon \operatorname {\mathrm {Spec}} k \to G$
,
![]() $i \colon G \to G$
given by
$i \colon G \to G$
given by
![]() $m^*(t_{i}) = t_{i} \otimes t_{i}$
,
$m^*(t_{i}) = t_{i} \otimes t_{i}$
,
![]() $e^*(t_{i}) = 1$
,
$e^*(t_{i}) = 1$
,
![]() $i^*(t_{i}) = t_{-i}$
.
$i^*(t_{i}) = t_{-i}$
.
An action
![]() $\alpha \colon G \times \operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} B$
corresponds, via
$\alpha \colon G \times \operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} B$
corresponds, via
![]() $\alpha ^*(b) = \sum _{i \in G^{\vee }} t_{i} \otimes \operatorname {\mathrm {pr}}_{i}(b)$
, to decompositions
$\alpha ^*(b) = \sum _{i \in G^{\vee }} t_{i} \otimes \operatorname {\mathrm {pr}}_{i}(b)$
, to decompositions
![]() $B = \bigoplus _{i \in G^{\vee }} B_i$
to k-vector subspaces satisfying
$B = \bigoplus _{i \in G^{\vee }} B_i$
to k-vector subspaces satisfying
![]() $B_i B_j \subset B_{i+j}$
. We say an element b or a subset of
$B_i B_j \subset B_{i+j}$
. We say an element b or a subset of
![]() $B_i$
to be homogeneous of weight i and we write
$B_i$
to be homogeneous of weight i and we write
![]() $\operatorname {\mathrm {wt}}(b) = i$
.
$\operatorname {\mathrm {wt}}(b) = i$
.
Such a decomposition
![]() $B = \bigoplus _{i} B_i$
naturally extends to a decomposition
$B = \bigoplus _{i} B_i$
naturally extends to a decomposition
![]() $\Omega ^*_{B/k} = \bigoplus _i (\Omega ^*_{B/k})_i$
satisfying
$\Omega ^*_{B/k} = \bigoplus _i (\Omega ^*_{B/k})_i$
satisfying
![]() $d(B_i) \subset (\Omega ^1_{B/k})_i$
and
$d(B_i) \subset (\Omega ^1_{B/k})_i$
and
![]() $(\Omega ^*_{B/k})_i (\Omega ^*_{B/k})_j \subset (\Omega ^*_{B/k})_{i+j}$
.
$(\Omega ^*_{B/k})_i (\Omega ^*_{B/k})_j \subset (\Omega ^*_{B/k})_{i+j}$
.
If G acts on a scheme X that is not necessarily affine but admits a covering by G-stable affine open subschemes (which is the case if, e.g., X is quasi-projective or G is local), then the G-action admits a quotient
![]() ${\pi }:{X} \to {X/G}$
, and induces decompositions
${\pi }:{X} \to {X/G}$
, and induces decompositions
![]() $\pi _* \mathcal {O}_X = \bigoplus _{i} (\pi _* \mathcal {O}_X)_i$
,
$\pi _* \mathcal {O}_X = \bigoplus _{i} (\pi _* \mathcal {O}_X)_i$
,
![]() $\pi _* \Omega ^*_{X/k} = \bigoplus _{i} (\pi _* \Omega ^*_{X/k})_i$
, and
$\pi _* \Omega ^*_{X/k} = \bigoplus _{i} (\pi _* \Omega ^*_{X/k})_i$
, and
![]() $H^0(X, (\Omega ^*_{X/k})^{\otimes n}) = \bigoplus _i (H^0(X, (\Omega ^*_{X/k})^{\otimes n}))_i$
, compatible with multiplications.
$H^0(X, (\Omega ^*_{X/k})^{\otimes n}) = \bigoplus _i (H^0(X, (\Omega ^*_{X/k})^{\otimes n}))_i$
, compatible with multiplications.
If
![]() $\operatorname {\mathrm {char}} k$
does not divide the order of
$\operatorname {\mathrm {char}} k$
does not divide the order of
![]() $G^{\vee }$
, then
$G^{\vee }$
, then
![]() $B_i$
are the eigenspaces for the action of
$B_i$
are the eigenspaces for the action of
![]() $G(k)$
with eigenvalues
$G(k)$
with eigenvalues
![]() $i \in G^{\vee }(k) = \operatorname {\mathrm {Hom}}(G(k),k^*)$
.
$i \in G^{\vee }(k) = \operatorname {\mathrm {Hom}}(G(k),k^*)$
.
If
![]() $\operatorname {\mathrm {char}} k = p> 0$
and
$\operatorname {\mathrm {char}} k = p> 0$
and
![]() $G^{\vee }$
is cyclic of order p (hence
$G^{\vee }$
is cyclic of order p (hence
![]() $G \cong \mu _p = \operatorname {\mathrm {Spec}} k[t_1]/(t_1^p - 1)$
for a choice of a generator
$G \cong \mu _p = \operatorname {\mathrm {Spec}} k[t_1]/(t_1^p - 1)$
for a choice of a generator
![]() $1$
of
$1$
of
![]() $G^{\vee }$
), then giving such a decomposition is also equivalent to giving a k-derivation D on B of multiplicative type (i.e.,
$G^{\vee }$
), then giving such a decomposition is also equivalent to giving a k-derivation D on B of multiplicative type (i.e.,
![]() $D^p = D$
) under the correspondence
$D^p = D$
) under the correspondence
![]() $B_i = B^{D = i} = \{b \in B \mid D(b) = ib \}$
(this correspondence depends on the choice of a generator
$B_i = B^{D = i} = \{b \in B \mid D(b) = ib \}$
(this correspondence depends on the choice of a generator
![]() $1$
of
$1$
of
![]() $G^{\vee }$
). Moreover, D extends to a k-linear endomorphism on
$G^{\vee }$
). Moreover, D extends to a k-linear endomorphism on
![]() $\Omega ^*_{B/k}$
satisfying
$\Omega ^*_{B/k}$
satisfying
![]() $D(df) = d(D(f))$
,
$D(df) = d(D(f))$
,
![]() $D^p = D$
, and the Leibniz rule
$D^p = D$
, and the Leibniz rule
![]() $D(\omega \wedge \eta ) = \omega \wedge D(\eta ) + D(\omega ) \wedge \eta $
.
$D(\omega \wedge \eta ) = \omega \wedge D(\eta ) + D(\omega ) \wedge \eta $
.
Now, we generalize the notion of symplecticness of automorphisms to actions of group schemes like
![]() $\mu _n$
.
$\mu _n$
.
Definition 2.5. Let G be a finite group scheme of multiplicative type. Let X be either an abelian surface or an RDP K3 surface, equipped with an action of G. We say that the action is symplectic if the one-dimensional space
![]() $H^0(X^{\mathrm {sm}}, \Omega ^2_{X/k})$
with respect to the action of G is of weight
$H^0(X^{\mathrm {sm}}, \Omega ^2_{X/k})$
with respect to the action of G is of weight
![]() $0$
.
$0$
.
Remark 2.6. Under the assumptions of Definition 2.5, suppose G is reduced. Equivalently, this means that G is a constant group scheme corresponding to a finite abelian group of order prime to p. Then, by Proposition 2.3, our symplecticness is equivalent to the symplecticness of the induced G-action on the minimal resolution
![]() $\tilde {X}$
in the usual sense (i.e., preserving the global
$\tilde {X}$
in the usual sense (i.e., preserving the global
![]() $2$
-form). This suggests that our definition of the symplecticness of
$2$
-form). This suggests that our definition of the symplecticness of
![]() $\mu _n$
-actions is a natural generalization of that of
$\mu _n$
-actions is a natural generalization of that of
![]() $\mathbb Z/m\mathbb Z$
-actions (order m automorphisms) for m not divisible by
$\mathbb Z/m\mathbb Z$
-actions (order m automorphisms) for m not divisible by
![]() $\operatorname {\mathrm {char}} k$
.
$\operatorname {\mathrm {char}} k$
.
On the other hand, if
![]() $G = \mathbb Z/p\mathbb Z$
(which does not belong to the class considered in Definition 2.5), then any action of G preserves the global
$G = \mathbb Z/p\mathbb Z$
(which does not belong to the class considered in Definition 2.5), then any action of G preserves the global
![]() $2$
-form, since there are no nontrivial pth roots of unity. Thus, the usual definition of symplecticness is useless in this case. We do not know whether there is a useful notion of symplecticness in a larger class of group schemes containing
$2$
-form, since there are no nontrivial pth roots of unity. Thus, the usual definition of symplecticness is useless in this case. We do not know whether there is a useful notion of symplecticness in a larger class of group schemes containing
![]() $\mathbb Z/p\mathbb Z$
or
$\mathbb Z/p\mathbb Z$
or
![]() $\alpha _p$
.
$\alpha _p$
.
2.3 Derivations of multiplicative type
In this section, assume that
![]() $\operatorname {\mathrm {char}} k = p> 0$
.
$\operatorname {\mathrm {char}} k = p> 0$
.
Recall that, given an action of a group scheme G on a scheme X, the fixed point scheme
![]() $X^G \subset X$
is characterized by the property
$X^G \subset X$
is characterized by the property
![]() $X^G(T) = \operatorname {\mathrm {Hom}}_G(T,X)$
for any k-scheme T equipped with the trivial G-action. If
$X^G(T) = \operatorname {\mathrm {Hom}}_G(T,X)$
for any k-scheme T equipped with the trivial G-action. If
![]() $G = \mu _p$
and D is the corresponding derivation, we write
$G = \mu _p$
and D is the corresponding derivation, we write
![]() $\operatorname {\mathrm {Fix}}(D) = X^G$
and also call it the fixed locus of D.
$\operatorname {\mathrm {Fix}}(D) = X^G$
and also call it the fixed locus of D.
Definition 2.7. We say that a closed point
![]() $w \in X$
is fixed by the
$w \in X$
is fixed by the
![]() $\mu _{n}$
-action, or by the corresponding derivation if
$\mu _{n}$
-action, or by the corresponding derivation if
![]() $n = p$
, if
$n = p$
, if
![]() $w \in X^{\mu _{n}}$
.
$w \in X^{\mu _{n}}$
.
Proposition 2.8. Let k be an algebraically closed field. Let
![]() $X = \operatorname {\mathrm {Spec}} B$
be a Noetherian affine k-scheme equipped with a
$X = \operatorname {\mathrm {Spec}} B$
be a Noetherian affine k-scheme equipped with a
![]() $\mu _{p^e}$
-action. For each closed point
$\mu _{p^e}$
-action. For each closed point
![]() $w \in X$
, the assertions (1)–(4) are equivalent. If
$w \in X$
, the assertions (1)–(4) are equivalent. If
![]() $e = 1$
and D is the corresponding derivation, then the assertions (1)–(6) are equivalent, and if moreover X is a smooth variety, then (7) is also equivalent.
$e = 1$
and D is the corresponding derivation, then the assertions (1)–(6) are equivalent, and if moreover X is a smooth variety, then (7) is also equivalent.
-
1. w is a
 $\mu _{p^e}$
-fixed point.
$\mu _{p^e}$
-fixed point. -
2. The maximal ideal
 $\mathfrak {m}_w$
of
$\mathfrak {m}_w$
of
 $\mathcal {O}_{X,w}$
is generated by homogeneous elements.
$\mathcal {O}_{X,w}$
is generated by homogeneous elements. -
3. The canonical morphism
 $B \to B / \mathfrak {m}_w$
is
$B \to B / \mathfrak {m}_w$
is
 $\mu _{p^e}$
-equivariant, where
$\mu _{p^e}$
-equivariant, where
 $B/\mathfrak {m}_w$
is equipped with the trivial action (i.e., the decomposition concentrated on
$B/\mathfrak {m}_w$
is equipped with the trivial action (i.e., the decomposition concentrated on
 $(-)_0$
).
$(-)_0$
). -
4.
 $B_i \subset \mathfrak {m}_w$
for each
$B_i \subset \mathfrak {m}_w$
for each
 $i \neq 0$
.
$i \neq 0$
. -
5.
 $D(\mathfrak {m}_w) \subset \mathfrak {m}_w$
.
$D(\mathfrak {m}_w) \subset \mathfrak {m}_w$
. -
6.
 $D(\mathcal {O}_{X,w}) \subset \mathfrak {m}_w$
.
$D(\mathcal {O}_{X,w}) \subset \mathfrak {m}_w$
. -
7. D has singularity at w in the sense of [Reference OgusRS, §1].
Finally, if (1) holds, then the
![]() $\mu _{p^e}$
-action extends to the blowup
$\mu _{p^e}$
-action extends to the blowup
![]() $\operatorname {\mathrm {Bl}}_w X$
.
$\operatorname {\mathrm {Bl}}_w X$
.
Proof. Let
![]() $B = \bigoplus _{i \in \mathbb Z/p^e\mathbb Z} B_i$
be the corresponding decomposition.
$B = \bigoplus _{i \in \mathbb Z/p^e\mathbb Z} B_i$
be the corresponding decomposition.
(1
![]() $\iff $
3) By the definition of
$\iff $
3) By the definition of
![]() $X^{\mu _p}$
, a closed point
$X^{\mu _p}$
, a closed point
![]() $w \in X$
is a (k-valued) point of
$w \in X$
is a (k-valued) point of
![]() $X^{\mu _p}$
if and only if
$X^{\mu _p}$
if and only if
![]() $B \to B/\mathfrak {m}_w$
is compatible with the projections
$B \to B/\mathfrak {m}_w$
is compatible with the projections
![]() $\operatorname {\mathrm {pr}}_i$
to the ith summand
$\operatorname {\mathrm {pr}}_i$
to the ith summand
![]() $(-)_i$
for all i, where
$(-)_i$
for all i, where
![]() $B/\mathfrak {m}_w$
is equipped with the trivial decomposition.
$B/\mathfrak {m}_w$
is equipped with the trivial decomposition.
(2
![]() $\iff $
3) If (3) holds, then we have
$\iff $
3) If (3) holds, then we have
![]() $\operatorname {\mathrm {pr}}_i(\mathfrak {m}_w) \subset \mathfrak {m}_w$
for all i, and then each element x of
$\operatorname {\mathrm {pr}}_i(\mathfrak {m}_w) \subset \mathfrak {m}_w$
for all i, and then each element x of
![]() $\mathfrak {m}_w$
is the sum of homogeneous elements
$\mathfrak {m}_w$
is the sum of homogeneous elements
![]() $\operatorname {\mathrm {pr}}_i(x) \in \mathfrak {m}_w$
. Conversely, if
$\operatorname {\mathrm {pr}}_i(x) \in \mathfrak {m}_w$
. Conversely, if
![]() $\mathfrak {m}_w$
is generated by homogeneous elements, then
$\mathfrak {m}_w$
is generated by homogeneous elements, then
![]() $\operatorname {\mathrm {pr}}_i(\mathfrak {m}_w) \subset \mathfrak {m}_w$
for all i, which implies (3).
$\operatorname {\mathrm {pr}}_i(\mathfrak {m}_w) \subset \mathfrak {m}_w$
for all i, which implies (3).
Assume
![]() $e = 1$
.
$e = 1$
.
(2
![]() $\iff $
5) Assume
$\iff $
5) Assume
![]() $D(\mathfrak {m}_w) \subset \mathfrak {m}_w$
. Take a system of generators
$D(\mathfrak {m}_w) \subset \mathfrak {m}_w$
. Take a system of generators
![]() $(x_j)$
of
$(x_j)$
of
![]() $\mathfrak {m}_w$
. For each j, let
$\mathfrak {m}_w$
. For each j, let
![]() $x_j = \sum _{i \in \mathbb F_p} x_{j,i}$
be the decomposition of
$x_j = \sum _{i \in \mathbb F_p} x_{j,i}$
be the decomposition of
![]() $x_j$
in
$x_j$
in
![]() $B = \bigoplus _{i} B_i$
. Then
$B = \bigoplus _{i} B_i$
. Then
![]() $D^l(x_j) = \sum _i i^l x_{j,i}$
is also in
$D^l(x_j) = \sum _i i^l x_{j,i}$
is also in
![]() $\mathfrak {m}_w$
. Since the matrix
$\mathfrak {m}_w$
. Since the matrix
![]() $(i^l)_{i,l=0}^{p-1}$
is invertible, this implies that
$(i^l)_{i,l=0}^{p-1}$
is invertible, this implies that
![]() $x_{j,i} \in \mathfrak {m}_w$
. Thus
$x_{j,i} \in \mathfrak {m}_w$
. Thus
![]() $\mathfrak {m}_w$
is generated by eigenvectors. The converse is clear.
$\mathfrak {m}_w$
is generated by eigenvectors. The converse is clear.
(5
![]() $\iff $
6) This is clear since
$\iff $
6) This is clear since
![]() $\mathcal {O}_{X,w} = \mathfrak {m}_w + k$
and
$\mathcal {O}_{X,w} = \mathfrak {m}_w + k$
and
![]() $D \rvert _{k} = 0$
.
$D \rvert _{k} = 0$
.
(5
![]() $\iff $
7) Take coordinates
$\iff $
7) Take coordinates
![]() $x_1, \ldots , x_n$
at a point w and write
$x_1, \ldots , x_n$
at a point w and write
![]() $D = \sum _j f_j \cdot (\partial / \partial x_j)$
. Then both of the conditions are equivalent to
$D = \sum _j f_j \cdot (\partial / \partial x_j)$
. Then both of the conditions are equivalent to
![]() $(f_j) \subset \mathfrak {m}_w$
.
$(f_j) \subset \mathfrak {m}_w$
.
We show the final assertion assuming (2). If the maximal ideal
![]() $\mathfrak {m}$
is generated by homogeneous elements
$\mathfrak {m}$
is generated by homogeneous elements
![]() $x_j \in B_{i_j}$
, then, for each j, we can extend the action on the affine piece
$x_j \in B_{i_j}$
, then, for each j, we can extend the action on the affine piece
![]() $\operatorname {\mathrm {Spec}} B[x_h/x_j]_h$
of
$\operatorname {\mathrm {Spec}} B[x_h/x_j]_h$
of
![]() $\operatorname {\mathrm {Bl}}_w X$
by declaring
$\operatorname {\mathrm {Bl}}_w X$
by declaring
![]() $x_h/x_j$
to be homogeneous of weight
$x_h/x_j$
to be homogeneous of weight
![]() $i_h - i_j$
.
$i_h - i_j$
.
The next lemma enables us to take useful coordinates at a point not fixed by D.
Lemma 2.9. If B is a Noetherian local ring, D is a derivation of multiplicative type, and the closed point is not fixed by D, then the maximal ideal
![]() $\mathfrak {m}$
of B is generated by elements
$\mathfrak {m}$
of B is generated by elements
![]() $x_1, \ldots , x_{m-1}, y$
with
$x_1, \ldots , x_{m-1}, y$
with
![]() $\operatorname {\mathrm {wt}}(x_j) = 0$
and
$\operatorname {\mathrm {wt}}(x_j) = 0$
and
![]() $\operatorname {\mathrm {wt}}(1+y) = 1$
. If
$\operatorname {\mathrm {wt}}(1+y) = 1$
. If
![]() $\mathfrak {m}$
is generated by n elements, then we can take
$\mathfrak {m}$
is generated by n elements, then we can take
![]() $m = n$
. If
$m = n$
. If
![]() $\dim B \geq 2$
, then D does not extend to a derivation of the blowup
$\dim B \geq 2$
, then D does not extend to a derivation of the blowup
![]() $\operatorname {\mathrm {Bl}}_{\mathfrak {m}} B$
.
$\operatorname {\mathrm {Bl}}_{\mathfrak {m}} B$
.
Proof. Recall that a subset of
![]() $\mathfrak {m}$
generates
$\mathfrak {m}$
generates
![]() $\mathfrak {m}$
if and only if it generates
$\mathfrak {m}$
if and only if it generates
![]() $\mathfrak {m}/\mathfrak {m}^2$
.
$\mathfrak {m}/\mathfrak {m}^2$
.
Take elements
![]() $x^{\prime }_1, \dots , x^{\prime }_m$
generating
$x^{\prime }_1, \dots , x^{\prime }_m$
generating
![]() $\mathfrak {m}$
, and let
$\mathfrak {m}$
, and let
![]() $x^{\prime }_j = \sum _{i \in \mathbb F_p} x^{\prime }_{j,i}$
be the decompositions to eigenvectors. By assumption, there exists a pair
$x^{\prime }_j = \sum _{i \in \mathbb F_p} x^{\prime }_{j,i}$
be the decompositions to eigenvectors. By assumption, there exists a pair
![]() $(j,i)$
with
$(j,i)$
with
![]() $x^{\prime }_{j,i} \not \in \mathfrak {m}$
. We take such
$x^{\prime }_{j,i} \not \in \mathfrak {m}$
. We take such
![]() $j_0,i_0$
, and we may assume
$j_0,i_0$
, and we may assume
![]() $i_0 \neq 0$
. We may assume
$i_0 \neq 0$
. We may assume
![]() $x^{\prime }_{j_0,i_0} - 1 \in \mathfrak {m}$
. Then
$x^{\prime }_{j_0,i_0} - 1 \in \mathfrak {m}$
. Then
![]() $y = x^{\prime }_{j_0,i_0} - 1 $
satisfies
$y = x^{\prime }_{j_0,i_0} - 1 $
satisfies
![]() $y \in \mathfrak {m}$
and
$y \in \mathfrak {m}$
and
![]() $D(y) = i_0 (y + 1)$
. We have
$D(y) = i_0 (y + 1)$
. We have
![]() $y \not \in \mathfrak {m}^2$
, since
$y \not \in \mathfrak {m}^2$
, since
![]() $D(\mathfrak {m}^2) \subset \mathfrak {m}$
. By replacing y with
$D(\mathfrak {m}^2) \subset \mathfrak {m}$
. By replacing y with
![]() $(y+1)^q - 1$
for an integer q with
$(y+1)^q - 1$
for an integer q with
![]() $q i_0 \equiv 1 \pmod p$
, we may assume
$q i_0 \equiv 1 \pmod p$
, we may assume
![]() $i_0 = 1$
. For each j, let
$i_0 = 1$
. For each j, let
![]() $x_j = \sum _i (y+1)^{-i} x^{\prime }_{j,i}$
. Then we have
$x_j = \sum _i (y+1)^{-i} x^{\prime }_{j,i}$
. Then we have
![]() $D(x_j) = 0$
and, since
$D(x_j) = 0$
and, since
![]() $x_j \equiv x^{\prime }_j \pmod {(y)}$
, the elements
$x_j \equiv x^{\prime }_j \pmod {(y)}$
, the elements
![]() $x_j,y$
generate
$x_j,y$
generate
![]() $\mathfrak {m}/\mathfrak {m}^2$
and hence generate
$\mathfrak {m}/\mathfrak {m}^2$
and hence generate
![]() $\mathfrak {m}$
. We can omit one of the
$\mathfrak {m}$
. We can omit one of the
![]() $x_j$
’s and then the remaining elements satisfies the required conditions (after renumbering).
$x_j$
’s and then the remaining elements satisfies the required conditions (after renumbering).
To show the latter assertion, it suffices to show that D does not extend to
![]() $B' := B[x_j/y]_j$
. If it extends, then we have
$B' := B[x_j/y]_j$
. If it extends, then we have
![]() $D(x_j/y) = -x_j(y+1)/y^2 \in B'$
, hence
$D(x_j/y) = -x_j(y+1)/y^2 \in B'$
, hence
![]() $x_j/y^2 \in B'$
, and then on
$x_j/y^2 \in B'$
, and then on
![]() $\operatorname {\mathrm {Spec}} B'$
we have that
$\operatorname {\mathrm {Spec}} B'$
we have that
![]() $y = 0$
implies
$y = 0$
implies
![]() $x_j/y = 0$
, which is impossible since
$x_j/y = 0$
, which is impossible since
![]() $\dim B' \geq 2$
.
$\dim B' \geq 2$
.
Before stating the next proposition, we recall the following notion from [Reference OgusRS]. Assume X is a smooth irreducible variety and D is a nontrivial derivation. Then
![]() $\operatorname {\mathrm {Fix}}(D)$
consists of its divisorial part
$\operatorname {\mathrm {Fix}}(D)$
consists of its divisorial part
![]() $(D)$
and non-divisorial part
$(D)$
and non-divisorial part
![]() $\langle D \rangle $
. If we write
$\langle D \rangle $
. If we write
![]() $D = f \sum _i g_i \frac {\partial }{\partial x_i}$
for some local coordinates
$D = f \sum _i g_i \frac {\partial }{\partial x_i}$
for some local coordinates
![]() $x_1, \dots , x_m$
with
$x_1, \dots , x_m$
with
![]() $g_i$
having no common factor, then
$g_i$
having no common factor, then
![]() $(D)$
and
$(D)$
and
![]() $\langle D \rangle $
correspond to the ideals
$\langle D \rangle $
correspond to the ideals
![]() $(f)$
and
$(f)$
and
![]() $(g_i)$
, respectively. If D is of multiplicative type with
$(g_i)$
, respectively. If D is of multiplicative type with
![]() $\langle D \rangle = \emptyset $
, then it follows from Proposition 2.8 that for suitable coordinates near any fixed point, we have
$\langle D \rangle = \emptyset $
, then it follows from Proposition 2.8 that for suitable coordinates near any fixed point, we have
![]() $D = a x_m \cdot (\partial / \partial x_m)$
and that
$D = a x_m \cdot (\partial / \partial x_m)$
and that
![]() $\operatorname {\mathrm {Fix}}(D)$
is a smooth divisor (possibly empty).
$\operatorname {\mathrm {Fix}}(D)$
is a smooth divisor (possibly empty).
Assuming that
![]() $\operatorname {\mathrm {Fix}}(D)$
is divisorial, in which case the quotient is a smooth variety by [Reference Rudakov and ShafarevichS, Prop. 6], the highest differential forms on smooth loci of X and
$\operatorname {\mathrm {Fix}}(D)$
is divisorial, in which case the quotient is a smooth variety by [Reference Rudakov and ShafarevichS, Prop. 6], the highest differential forms on smooth loci of X and
![]() $X^D$
are related in the following way.
$X^D$
are related in the following way.
Proposition 2.10. Let X be a smooth variety of dimension m (not necessarily proper) equipped with a nontrivial derivation D of multiplicative type such that
![]() $\operatorname {\mathrm {Fix}}(D)$
is divisorial. Let
$\operatorname {\mathrm {Fix}}(D)$
is divisorial. Let
![]() $\Delta $
be the divisor
$\Delta $
be the divisor
![]() $\operatorname {\mathrm {Fix}}(D)$
. Then there is a unique collection of isomorphisms
$\operatorname {\mathrm {Fix}}(D)$
. Then there is a unique collection of isomorphisms
for all integers n, compatible with multiplication, preserving the zero loci, and sending (for
![]() $n = 1$
)
$n = 1$
)
if
![]() $f_0, \dots , f_{m-1}$
are homogeneous of weight
$f_0, \dots , f_{m-1}$
are homogeneous of weight
![]() $0$
and
$0$
and
![]() $f_m$
is homogeneous of some weight (not necessarily
$f_m$
is homogeneous of some weight (not necessarily
![]() $0$
).
$0$
).
In particular, if the action is fixed-point-free, then we have isomorphisms
 $$ \begin{align*} (\pi_* (\Omega^m_{X/k})^{\otimes n})_0 &\cong (\Omega^m_{X^D/k})^{\otimes n} \quad \text{and} \\ H^0(X, (\Omega^m_{X/k})^{\otimes n})_0 &\cong H^0(X^D, (\Omega^m_{X^D/k})^{\otimes n}) \end{align*} $$
$$ \begin{align*} (\pi_* (\Omega^m_{X/k})^{\otimes n})_0 &\cong (\Omega^m_{X^D/k})^{\otimes n} \quad \text{and} \\ H^0(X, (\Omega^m_{X/k})^{\otimes n})_0 &\cong H^0(X^D, (\Omega^m_{X^D/k})^{\otimes n}) \end{align*} $$
with the same properties.
Proof. The isomorphism for
![]() $n = 0$
is clear. It suffices to construct the isomorphism for
$n = 0$
is clear. It suffices to construct the isomorphism for
![]() $n = 1$
that is compatible with multiplication with
$n = 1$
that is compatible with multiplication with
![]() $n = 0$
forms and with restriction to open subschemes.
$n = 0$
forms and with restriction to open subschemes.
Take a closed point
![]() $w \in X$
. Let
$w \in X$
. Let
![]() $\varepsilon = 1$
(resp.
$\varepsilon = 1$
(resp.
![]() $\varepsilon = 0$
) if
$\varepsilon = 0$
) if
![]() $w \not \in \Delta $
(resp.
$w \not \in \Delta $
(resp.
![]() $w \in \Delta $
). By Lemma 2.9 (resp. by [Reference OgusRS, Th. 1]), there are coordinates
$w \in \Delta $
). By Lemma 2.9 (resp. by [Reference OgusRS, Th. 1]), there are coordinates
![]() $x_1, \dots , x_m$
on a neighborhood of w with
$x_1, \dots , x_m$
on a neighborhood of w with
![]() $D(x_j) = 0$
for
$D(x_j) = 0$
for
![]() $j < m$
and
$j < m$
and
![]() $D(x_m) = a (\varepsilon + x_m)$
for some
$D(x_m) = a (\varepsilon + x_m)$
for some
![]() $a \in \mathbb F_p^*$
. We define
$a \in \mathbb F_p^*$
. We define
 $$ \begin{align*} \phi \colon (\pi_* (\Omega^m_{X/k}(\Delta)))_0 &\to \Omega^m_{X^D/k}(\pi_*(\Delta)) \\ f \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m) &\mapsto f \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m^p) \end{align*} $$
$$ \begin{align*} \phi \colon (\pi_* (\Omega^m_{X/k}(\Delta)))_0 &\to \Omega^m_{X^D/k}(\pi_*(\Delta)) \\ f \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m) &\mapsto f \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m^p) \end{align*} $$
for f of weight
![]() $0$
(note that
$0$
(note that
![]() $dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log (\varepsilon + x_m)$
is a local generator of the left-hand side). We show that then
$dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log (\varepsilon + x_m)$
is a local generator of the left-hand side). We show that then
![]() $\phi $
sends
$\phi $
sends
for any
![]() $f_0, \dots , f_{m-1}$
and
$f_0, \dots , f_{m-1}$
and
![]() $f_m$
as in the statement. This implies that
$f_m$
as in the statement. This implies that
![]() $\phi $
does not depend on the choice of the coordinates and hence that
$\phi $
does not depend on the choice of the coordinates and hence that
![]() $\phi $
induces a well-defined morphism of sheaves. Then since
$\phi $
induces a well-defined morphism of sheaves. Then since
![]() $dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log (\varepsilon + x_m)$
(resp.
$dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log (\varepsilon + x_m)$
(resp.
![]() $dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log (\varepsilon + x_m^p)$
) is a local generator of
$dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log (\varepsilon + x_m^p)$
) is a local generator of
![]() $(\Omega ^m_{X/k}(\Delta ))_0$
(resp.
$(\Omega ^m_{X/k}(\Delta ))_0$
(resp.
![]() $\Omega ^m_{X^D/k}(\pi _*(\Delta ))$
), it follows that
$\Omega ^m_{X^D/k}(\pi _*(\Delta ))$
), it follows that
![]() $\phi $
is an isomorphism and
$\phi $
is an isomorphism and
![]() $\phi ^{\otimes n}$
are well-defined isomorphisms.
$\phi ^{\otimes n}$
are well-defined isomorphisms.
We may pass to the completion, so consider
![]() $f_h \in k[[x_1, \dots , x_m]]$
. By the assumption on the weight, we have
$f_h \in k[[x_1, \dots , x_m]]$
. By the assumption on the weight, we have
![]() $f_h \in k[[x_1, \dots , x_{m-1}, x_m^p]]$
for
$f_h \in k[[x_1, \dots , x_{m-1}, x_m^p]]$
for
![]() $h < m$
and
$h < m$
and
![]() $f_m \in (\varepsilon + x_m)^b k[[x_1, \dots , x_{m-1}, x_m^p]]$
for some
$f_m \in (\varepsilon + x_m)^b k[[x_1, \dots , x_{m-1}, x_m^p]]$
for some
![]() $0 \leq b < p$
. Then we have
$0 \leq b < p$
. Then we have
![]() $\partial f_h / \partial x_m = 0$
for
$\partial f_h / \partial x_m = 0$
for
![]() $h < m$
and
$h < m$
and
![]() $\partial f_m / \partial x_m = b f_m/(\varepsilon + x_m)$
. Hence, we have
$\partial f_m / \partial x_m = b f_m/(\varepsilon + x_m)$
. Hence, we have
 $$ \begin{align*} & f_0 \cdot df_1 \wedge \dots \wedge df_{m-1} \wedge d\log(f_m) \\ &= f_0 ((\varepsilon + x_m)/f_m) \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m) \\ &= b f_0 \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m-1} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m) \\ &\stackrel{\phi}{\mapsto} b f_0 \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m-1} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m^p). \end{align*} $$
$$ \begin{align*} & f_0 \cdot df_1 \wedge \dots \wedge df_{m-1} \wedge d\log(f_m) \\ &= f_0 ((\varepsilon + x_m)/f_m) \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m) \\ &= b f_0 \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m-1} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m) \\ &\stackrel{\phi}{\mapsto} b f_0 \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m-1} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m^p). \end{align*} $$
On the other hand, in the invariant subalgebra
![]() $k[[x_1, \dots , x_{m-1}, x_m^p]]$
, we have
$k[[x_1, \dots , x_{m-1}, x_m^p]]$
, we have
![]() $\partial f_m^p / \partial x_j = 0$
for
$\partial f_m^p / \partial x_j = 0$
for
![]() $j < m$
and
$j < m$
and
![]() $\partial f_m^p / \partial x_m^p = b f_m^p/(\varepsilon + x_m^p)$
. Hence, we have
$\partial f_m^p / \partial x_m^p = b f_m^p/(\varepsilon + x_m^p)$
. Hence, we have
 $$ \begin{align*} & f_0 \cdot df_1 \wedge \dots \wedge df_{m-1} \wedge d\log(f_m^p) \\ &= \dots = b f_0 \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m-1} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m^p). \end{align*} $$
$$ \begin{align*} & f_0 \cdot df_1 \wedge \dots \wedge df_{m-1} \wedge d\log(f_m^p) \\ &= \dots = b f_0 \det (\partial f_h / \partial x_j)_{1 \leq h,j \leq m-1} \cdot dx_1 \wedge \dots \wedge dx_{m-1} \wedge d\log(\varepsilon + x_m^p). \end{align*} $$
The assertion follows.
We will give another abstract proof of Proposition 2.10 in [Reference MatsumotoMat3, Prop. 2.12].
2.4 Global properties of derivations
Lemma 2.11. Let
![]() $C \subset \mathbb P^2$
be a quadratic curve (not necessarily irreducible nor reduced) in characteristic p, and let D be a p-closed derivation. Then
$C \subset \mathbb P^2$
be a quadratic curve (not necessarily irreducible nor reduced) in characteristic p, and let D be a p-closed derivation. Then
![]() $\operatorname {\mathrm {Fix}}(D) \neq \emptyset $
.
$\operatorname {\mathrm {Fix}}(D) \neq \emptyset $
.
Proof. Suppose C is integral. Then
![]() $C \cong \mathbb P^1$
and the result is well known (indeed,
$C \cong \mathbb P^1$
and the result is well known (indeed,
![]() $T_{\mathbb P^1} \cong \mathcal {O}_{\mathbb P^1}(2)$
).
$T_{\mathbb P^1} \cong \mathcal {O}_{\mathbb P^1}(2)$
).
Suppose C is reducible. We may assume
![]() $C = (xy = 0)$
. Let
$C = (xy = 0)$
. Let
![]() $U = \operatorname {\mathrm {Spec}} k[x,y] / (xy)$
. Then
$U = \operatorname {\mathrm {Spec}} k[x,y] / (xy)$
. Then
![]() $T_U = ( x \frac {d}{dx} - y \frac {d}{dy}) \cdot \mathcal {O}_U$
and hence the origin belongs to
$T_U = ( x \frac {d}{dx} - y \frac {d}{dy}) \cdot \mathcal {O}_U$
and hence the origin belongs to
![]() $\operatorname {\mathrm {Fix}}(D)$
.
$\operatorname {\mathrm {Fix}}(D)$
.
Suppose C is non-reduced. We may assume
![]() $C = (X_3^2 = 0)$
. If
$C = (X_3^2 = 0)$
. If
![]() $p \neq 2$
, then D induces a derivation
$p \neq 2$
, then D induces a derivation
![]() $D_{\mathrm {red}}$
on
$D_{\mathrm {red}}$
on
![]() $C_{\mathrm {red}} \cong \mathbb P^1$
, and we have
$C_{\mathrm {red}} \cong \mathbb P^1$
, and we have
![]() $\operatorname {\mathrm {Fix}}(D) \approx \operatorname {\mathrm {Fix}}(D_{\mathrm {red}}) \neq \emptyset $
. Suppose
$\operatorname {\mathrm {Fix}}(D) \approx \operatorname {\mathrm {Fix}}(D_{\mathrm {red}}) \neq \emptyset $
. Suppose
![]() $p = 2$
. It is easy to see that
$p = 2$
. It is easy to see that
![]() $H^0(C, T_C) \stackrel {\sim }{\to } H^0(C, T_{\mathbb P^2} \rvert _{C}) \stackrel {\sim }{\leftarrow } H^0(\mathbb P^2, T_{\mathbb P^2})$
. Hence, there exist
$H^0(C, T_C) \stackrel {\sim }{\to } H^0(C, T_{\mathbb P^2} \rvert _{C}) \stackrel {\sim }{\leftarrow } H^0(\mathbb P^2, T_{\mathbb P^2})$
. Hence, there exist
![]() $f_1, f_2, f_3 \in H^0(\mathbb P^2, \mathcal {O}(1)) = \bigoplus _{i=1}^3 k X_i$
such that
$f_1, f_2, f_3 \in H^0(\mathbb P^2, \mathcal {O}(1)) = \bigoplus _{i=1}^3 k X_i$
such that
![]() $D\bigl (\frac {X_i}{X_j}\bigr ) = \frac {f_i}{X_j} - \frac {X_i f_j}{X_j^2}$
. If
$D\bigl (\frac {X_i}{X_j}\bigr ) = \frac {f_i}{X_j} - \frac {X_i f_j}{X_j^2}$
. If
![]() $f_3 \in k X_3$
, then D induces a derivation
$f_3 \in k X_3$
, then D induces a derivation
![]() $D_{\mathrm {red}}$
on
$D_{\mathrm {red}}$
on
![]() $C_{\mathrm {red}} \cong \mathbb P^1$
, and we conclude as above. Suppose
$C_{\mathrm {red}} \cong \mathbb P^1$
, and we conclude as above. Suppose
![]() $f_3 \not \in k X_3$
. By a coordinate change, we may assume
$f_3 \not \in k X_3$
. By a coordinate change, we may assume
![]() $f_3 - X_2 \in k X_3$
. Letting
$f_3 - X_2 \in k X_3$
. Letting
![]() $x_i = X_i/X_1$
(
$x_i = X_i/X_1$
(
![]() $i = 2,3$
) and restricting to
$i = 2,3$
) and restricting to
![]() $\operatorname {\mathrm {Spec}} k[x_2,x_3]/(x_3^2) = (X_1 \neq 0) \subset C$
, we have
$\operatorname {\mathrm {Spec}} k[x_2,x_3]/(x_3^2) = (X_1 \neq 0) \subset C$
, we have
![]() $D(x_3) - x_2 \in (x_3)$
, in particular
$D(x_3) - x_2 \in (x_3)$
, in particular
![]() $D(x_3) \in \mathfrak {m} := (x_2, x_3)$
. If
$D(x_3) \in \mathfrak {m} := (x_2, x_3)$
. If
![]() $D(x_2) \in \mathfrak {m}$
, then the origin is a fixed point. Suppose
$D(x_2) \in \mathfrak {m}$
, then the origin is a fixed point. Suppose
![]() $D(x_2) \not \in \mathfrak {m}$
and
$D(x_2) \not \in \mathfrak {m}$
and
![]() $D^2 = h D$
. Then
$D^2 = h D$
. Then
![]() $h = D^2(x_2) / D(x_2) \in \mathcal {O}_{\mathfrak {m}}$
, and hence
$h = D^2(x_2) / D(x_2) \in \mathcal {O}_{\mathfrak {m}}$
, and hence
![]() $D(x_2) \equiv D^2(x_3) = h D(x_3) \equiv 0 \pmod {\mathfrak {m}}$
, contradiction.
$D(x_2) \equiv D^2(x_3) = h D(x_3) \equiv 0 \pmod {\mathfrak {m}}$
, contradiction.
Corollary 2.12. Suppose
![]() $\mu _p$
acts on an RDP surface X and fixes an RDP w. Then the action extends to the blowup
$\mu _p$
acts on an RDP surface X and fixes an RDP w. Then the action extends to the blowup
![]() $\operatorname {\mathrm {Bl}}_w X$
and there exists a fixed point above w.
$\operatorname {\mathrm {Bl}}_w X$
and there exists a fixed point above w.
Proof. The action extends to the blowup by Proposition 2.8. Let
![]() $D'$
be the induced derivation on
$D'$
be the induced derivation on
![]() $\operatorname {\mathrm {Bl}}_w X$
. Let
$\operatorname {\mathrm {Bl}}_w X$
. Let
![]() $C \subset \operatorname {\mathrm {Bl}}_w X$
be the (possibly non-reduced) exceptional divisor, which is a quadratic curve in
$C \subset \operatorname {\mathrm {Bl}}_w X$
be the (possibly non-reduced) exceptional divisor, which is a quadratic curve in
![]() $\mathbb P^2$
since w is an RDP. Since
$\mathbb P^2$
since w is an RDP. Since
![]() $D'(\mathcal I_C) \subset \mathcal I_C$
,
$D'(\mathcal I_C) \subset \mathcal I_C$
,
![]() $D'$
induces a derivation
$D'$
induces a derivation
![]() $D^{\prime }_{C}$
(of multiplicative type) on C. By Lemma 2.11,
$D^{\prime }_{C}$
(of multiplicative type) on C. By Lemma 2.11,
![]() $D^{\prime }_C$
has at least one fixed point, and that point is also a fixed point of
$D^{\prime }_C$
has at least one fixed point, and that point is also a fixed point of
![]() $D'$
.
$D'$
.
Later we will also need the following Katsura–Takeda formula on rational vector fields (i.e., derivations on the fraction field
![]() $k(X)$
). For a rational derivation D locally of the form
$k(X)$
). For a rational derivation D locally of the form
![]() $f^{-1} D'$
for some regular function f and (regular) derivation
$f^{-1} D'$
for some regular function f and (regular) derivation
![]() $D'$
, we define the divisorial and nondivisorial parts by
$D'$
, we define the divisorial and nondivisorial parts by
![]() $(D) = (D') - \operatorname {\mathrm {div}}(f)$
and
$(D) = (D') - \operatorname {\mathrm {div}}(f)$
and
![]() $\langle D \rangle = \langle D' \rangle $
.
$\langle D \rangle = \langle D' \rangle $
.
Proposition 2.13 [Reference KatsuraKT, Prop. 2.1]
Let X be a smooth proper surface, and let D be a nonzero rational vector field. Then we have
3 Tame symplectic actions on RDPs
Hereafter, all action of groups and group schemes on schemes are assumed faithful.
Throughout this section, we work under the following setting.
![]() $B = \mathcal {O}_{X,w}$
is the localization of an RDP surface X over an algebraically closed field k at a closed point w (either a smooth point or an RDP),
$B = \mathcal {O}_{X,w}$
is the localization of an RDP surface X over an algebraically closed field k at a closed point w (either a smooth point or an RDP),
![]() $\mathfrak {m} \subset B$
is the maximal ideal, G is a finite group acting on X, and the action restricts to
$\mathfrak {m} \subset B$
is the maximal ideal, G is a finite group acting on X, and the action restricts to
![]() $\operatorname {\mathrm {Spec}} B$
. Assume that the order of G is not divisible by
$\operatorname {\mathrm {Spec}} B$
. Assume that the order of G is not divisible by
![]() $p = \operatorname {\mathrm {char}} k$
.
$p = \operatorname {\mathrm {char}} k$
.
Definition 3.1. We say that the G-action on B is symplectic if it acts on the one-dimensional k-vector space
![]() $H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k}) \otimes _B (B/\mathfrak {m})$
trivially.
$H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k}) \otimes _B (B/\mathfrak {m})$
trivially.
If
![]() $G = \mathbb Z/p\mathbb Z$
, then any action is symplectic (cf. Remark 2.6), and hence the notion is useless in this case.
$G = \mathbb Z/p\mathbb Z$
, then any action is symplectic (cf. Remark 2.6), and hence the notion is useless in this case.
Remark 3.2. If B is as above and the G-action is symplectic, then the rank-
![]() $1$
free B-module
$1$
free B-module
![]() $H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
admits a generator
$H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
admits a generator
![]() $\omega $
that is G-invariant. Indeed, take a generator
$\omega $
that is G-invariant. Indeed, take a generator
![]() $\omega '$
, then
$\omega '$
, then
![]() $\omega := (1 / \lvert G \rvert ) \sum _{g \in G} g^* \omega '$
is clearly G-invariant and it is nonvanishing, since it is nonvanishing after
$\omega := (1 / \lvert G \rvert ) \sum _{g \in G} g^* \omega '$
is clearly G-invariant and it is nonvanishing, since it is nonvanishing after
![]() $\otimes (B / \mathfrak {m})$
.
$\otimes (B / \mathfrak {m})$
.
Remark 3.3. If X is an RDP K3 surface and
![]() $w \in X$
is a fixed closed point, then this is consistent with the usual notion of symplecticness, since a generator of
$w \in X$
is a fixed closed point, then this is consistent with the usual notion of symplecticness, since a generator of
![]() $H^0(X^{\mathrm {sm}}, \Omega ^2) \cong H^0(\tilde {X}, \Omega ^2)$
(Proposition 2.3) restricts to a generator of this one-dimensional space. Thus, the symplecticness of an automorphism of an RDP K3 surface can be checked locally at any fixed point (if there exists any). The same for abelian surfaces.
$H^0(X^{\mathrm {sm}}, \Omega ^2) \cong H^0(\tilde {X}, \Omega ^2)$
(Proposition 2.3) restricts to a generator of this one-dimensional space. Thus, the symplecticness of an automorphism of an RDP K3 surface can be checked locally at any fixed point (if there exists any). The same for abelian surfaces.
Proposition 3.4. Let B and G be as above (in particular, the order of G is not divisible by
![]() $p = \operatorname {\mathrm {char}} k$
). Then the invariant ring
$p = \operatorname {\mathrm {char}} k$
). Then the invariant ring
![]() $B^G$
is again the localization at a closed point of an RDP surface.
$B^G$
is again the localization at a closed point of an RDP surface.
Let
![]() $\tilde {X} \to X$
be the minimal resolution at w. Then
$\tilde {X} \to X$
be the minimal resolution at w. Then
![]() $\tilde {X}/G \to X/G$
is crepant.
$\tilde {X}/G \to X/G$
is crepant.
Proof. Let
![]() $\omega $
be a generator of the rank-
$\omega $
be a generator of the rank-
![]() $1$
free B-module
$1$
free B-module
![]() $H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
. By Remark 3.2, we may assume
$H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
. By Remark 3.2, we may assume
![]() $\omega $
is G-invariant. The action of G on X induces an action on
$\omega $
is G-invariant. The action of G on X induces an action on
![]() $\tilde {X}$
, and
$\tilde {X}$
, and
![]() $\omega $
extends to a regular nonvanishing
$\omega $
extends to a regular nonvanishing
![]() $2$
-form on
$2$
-form on
![]() $\tilde {X}$
. At each closed point
$\tilde {X}$
. At each closed point
![]() $w' \in \tilde {X}$
, the stabilizer
$w' \in \tilde {X}$
, the stabilizer
![]() $G_{w'} \subset G$
acts on
$G_{w'} \subset G$
acts on
![]() $T_{w'} \tilde {X}$
via
$T_{w'} \tilde {X}$
via
![]() $\operatorname {\mathrm {SL}}_2(k)$
since G preserves
$\operatorname {\mathrm {SL}}_2(k)$
since G preserves
![]() $\omega $
. Hence, the quotient
$\omega $
. Hence, the quotient
![]() $\tilde {X}/G$
has only RDPs as singularities. Since
$\tilde {X}/G$
has only RDPs as singularities. Since
![]() $\omega $
is preserved by G, it induces a regular nonvanishing
$\omega $
is preserved by G, it induces a regular nonvanishing
![]() $2$
-form on
$2$
-form on
![]() $(\tilde {X}/G)^{\mathrm {sm}}$
, and since RDPs are canonical singularities, it extends to a regular nonvanishing
$(\tilde {X}/G)^{\mathrm {sm}}$
, and since RDPs are canonical singularities, it extends to a regular nonvanishing
![]() $2$
-form on
$2$
-form on
![]() $\widetilde {\tilde {X}/G}$
, the minimal resolution of
$\widetilde {\tilde {X}/G}$
, the minimal resolution of
![]() $\tilde {X}/G$
above w. Thus,
$\tilde {X}/G$
above w. Thus,
![]() $B^G$
is a canonical singularity, that is, either a smooth point or an RDP.
$B^G$
is a canonical singularity, that is, either a smooth point or an RDP.
Remark 3.5. We [Reference Madapusi PeraMat1, Prop. 3.8] described possible symplectic actions of finite tame groups on RDPs. For actions of cyclic groups
![]() $G = \mathbb Z/n\mathbb Z$
(
$G = \mathbb Z/n\mathbb Z$
(
![]() $n> 1$
), we have a complete classification: possible n and the types of X and
$n> 1$
), we have a complete classification: possible n and the types of X and
![]() $X/G$
are listed in Table 2.
$X/G$
are listed in Table 2.
Table 2 Tame symplectic cyclic actions on RDPs.

Remark 3.6. Singularities of quotients by order p automorphisms in characteristic
![]() $p> 0$
tends to be worse than those in characteristic
$p> 0$
tends to be worse than those in characteristic
![]() $\neq p$
. For example, the quotient of a supersingular abelian surface in characteristic
$\neq p$
. For example, the quotient of a supersingular abelian surface in characteristic
![]() $2$
by the automorphism
$2$
by the automorphism
![]() $x \mapsto -x$
is a rational surface with an elliptic singularity [Reference JangKa, Th. C].
$x \mapsto -x$
is a rational surface with an elliptic singularity [Reference JangKa, Th. C].
4
 $\mu _n$
-actions on RDPs and quotients
$\mu _n$
-actions on RDPs and quotients
Throughout this section, we work under the following setting.
![]() $B = \mathcal {O}_{X,w}$
is the localization of an RDP surface X over an algebraically closed field k of characteristic
$B = \mathcal {O}_{X,w}$
is the localization of an RDP surface X over an algebraically closed field k of characteristic
![]() $p \geq 0$
at a closed point w (either a smooth point or an RDP),
$p \geq 0$
at a closed point w (either a smooth point or an RDP),
![]() $\mathfrak {m} \subset B$
is the maximal ideal, n is a positive integer possibly divisible by p,
$\mathfrak {m} \subset B$
is the maximal ideal, n is a positive integer possibly divisible by p,
![]() $\mu _n$
acts on X, and the action restricts to
$\mu _n$
acts on X, and the action restricts to
![]() $\operatorname {\mathrm {Spec}} B$
. (Note that w is not necessarily fixed by
$\operatorname {\mathrm {Spec}} B$
. (Note that w is not necessarily fixed by
![]() $\mu _n$
.)
$\mu _n$
.)
If
![]() $n = p> 0$
, then the corresponding derivation of multiplicative type is denoted by D.
$n = p> 0$
, then the corresponding derivation of multiplicative type is denoted by D.
4.1 Symplecticness of
 $\mu _n$
-actions
$\mu _n$
-actions
Assume w is fixed by the
![]() $\mu _n$
-action. Then the action on B induces an action on
$\mu _n$
-action. Then the action on B induces an action on
![]() $V := H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k}) \otimes _B (B/\mathfrak {m})$
, that is, a decomposition
$V := H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k}) \otimes _B (B/\mathfrak {m})$
, that is, a decomposition
![]() $V = \bigoplus _{i \in \mathbb Z/n\mathbb Z} V_i$
of k-vector spaces. Since
$V = \bigoplus _{i \in \mathbb Z/n\mathbb Z} V_i$
of k-vector spaces. Since
![]() $\dim _k V = 1$
, V is equal to one of the summands. In other words, V is of some weight
$\dim _k V = 1$
, V is equal to one of the summands. In other words, V is of some weight
![]() $i_0 \in \mathbb Z/n\mathbb Z$
.
$i_0 \in \mathbb Z/n\mathbb Z$
.
Definition 4.1. We say that the
![]() $\mu _{n}$
-action, or the corresponding derivation if
$\mu _{n}$
-action, or the corresponding derivation if
![]() $n = p$
, on B is symplectic if V is of weight
$n = p$
, on B is symplectic if V is of weight
![]() $0$
.
$0$
.
We say that a
![]() $\mu _{n}$
-action, or a derivation D of multiplicative type, on an RDP surface X is symplectic at a fixed closed point w if the induced action or derivation on
$\mu _{n}$
-action, or a derivation D of multiplicative type, on an RDP surface X is symplectic at a fixed closed point w if the induced action or derivation on
![]() $\mathcal {O}_{X,w}$
is symplectic in the above sense.
$\mathcal {O}_{X,w}$
is symplectic in the above sense.
Remark 4.2. If
![]() $p \nmid n$
, then
$p \nmid n$
, then
![]() $\mu _n$
is (noncanonically) isomorphic to
$\mu _n$
is (noncanonically) isomorphic to
![]() $\mathbb Z/n\mathbb Z$
and this definition is consistent with Definition 3.1.
$\mathbb Z/n\mathbb Z$
and this definition is consistent with Definition 3.1.
Remark 4.3 (cf. Remark 3.2)
If B is as above and V is of weight
![]() $i_0$
, then the rank-
$i_0$
, then the rank-
![]() $1$
free B-module
$1$
free B-module
![]() $H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
admits a generator
$H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
admits a generator
![]() $\omega $
of weight
$\omega $
of weight
![]() $i_0$
. Indeed, take a generator
$i_0$
. Indeed, take a generator
![]() $\omega '$
, let
$\omega '$
, let
![]() $\omega ' = \sum _{i} \omega ^{\prime }_i$
be its decomposition, and write
$\omega ' = \sum _{i} \omega ^{\prime }_i$
be its decomposition, and write
![]() $\omega ^{\prime }_i = f_i \omega '$
with
$\omega ^{\prime }_i = f_i \omega '$
with
![]() $f_i \in B$
. Since
$f_i \in B$
. Since
![]() $\sum f_i = 1$
, there exists
$\sum f_i = 1$
, there exists
![]() $i_1 \in \mathbb Z/n\mathbb Z$
with
$i_1 \in \mathbb Z/n\mathbb Z$
with
![]() $f_{i_1} \in B^*$
. Then
$f_{i_1} \in B^*$
. Then
![]() $i_0 = i_1$
and hence we can take
$i_0 = i_1$
and hence we can take
![]() $\omega = \omega ^{\prime }_{i_1}$
. If
$\omega = \omega ^{\prime }_{i_1}$
. If
![]() $n = p$
, then this means
$n = p$
, then this means
![]() $D(\omega ) = i_0 \omega $
.
$D(\omega ) = i_0 \omega $
.
From this, it follows that if
![]() $\mu _{n}$
acts on an RDP surface, then the weight
$\mu _{n}$
acts on an RDP surface, then the weight
![]() $i_0$
is a locally constant function on the fixed locus.
$i_0$
is a locally constant function on the fixed locus.
Remark 4.4 (cf. Remark 3.3)
If X is an RDP K3 surface and
![]() $w \in X$
is a fixed closed point, then the action is symplectic in the sense of Definition 2.5 if and only if action is symplectic at w, since a generator of
$w \in X$
is a fixed closed point, then the action is symplectic in the sense of Definition 2.5 if and only if action is symplectic at w, since a generator of
![]() $H^0(X^{\mathrm {sm}}, \Omega ^2)$
restricts to a generator of this one-dimensional space. Thus, the symplecticness of a
$H^0(X^{\mathrm {sm}}, \Omega ^2)$
restricts to a generator of this one-dimensional space. Thus, the symplecticness of a
![]() $\mu _{n}$
-action on an RDP K3 surface can be checked locally at any fixed point (if there exists any). The same for abelian surfaces.
$\mu _{n}$
-action on an RDP K3 surface can be checked locally at any fixed point (if there exists any). The same for abelian surfaces.
Lemma 4.5. Suppose the closed point w of B is fixed under the
![]() $\mu _n$
-action. Then B is generated by
$\mu _n$
-action. Then B is generated by
![]() $2$
or
$2$
or
![]() $3$
homogeneous elements, respectively, if B is smooth or an RDP. Moreover:
$3$
homogeneous elements, respectively, if B is smooth or an RDP. Moreover:
-
1. If B is smooth and generated by elements
 $x,y$
of respective weights
$x,y$
of respective weights
 $a,b$
, then the action is symplectic if and only if
$a,b$
, then the action is symplectic if and only if
 $a + b = 0$
(in
$a + b = 0$
(in
 $\mathbb Z/n\mathbb Z$
).
$\mathbb Z/n\mathbb Z$
). -
2. If B is an RDP and generated by
 $x,y,z$
of respective weights
$x,y,z$
of respective weights
 $a,b,c$
, then there is
$a,b,c$
, then there is
 $d \in \mathbb Z/n\mathbb Z$
and a homogeneous power series
$d \in \mathbb Z/n\mathbb Z$
and a homogeneous power series
 $F \in k[[x,y,z]]$
of weight d such that
$F \in k[[x,y,z]]$
of weight d such that
 $\hat {B} \cong k[[x,y,z]]/(F)$
. The action is symplectic if and only if
$\hat {B} \cong k[[x,y,z]]/(F)$
. The action is symplectic if and only if
 $a + b + c = d$
.
$a + b + c = d$
.
Proof. The first assertion follows from Proposition 2.8.
(1)
![]() $H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
is generated by
$H^0(\operatorname {\mathrm {Spec}} B \setminus \{\mathfrak {m}\}, \Omega ^2_{B/k})$
is generated by
![]() $dx \wedge dy$
, which is of weight
$dx \wedge dy$
, which is of weight
![]() $a+b$
.
$a+b$
.
(2) Take an element
![]() $H \in k[[x,y,z]]$
such that
$H \in k[[x,y,z]]$
such that
![]() $\hat {B} = k[[x,y,z]] / (H)$
, and let
$\hat {B} = k[[x,y,z]] / (H)$
, and let
![]() $H = \sum _{i \in \mathbb Z/n\mathbb Z} H_i$
be the decomposition with respect to the
$H = \sum _{i \in \mathbb Z/n\mathbb Z} H_i$
be the decomposition with respect to the
![]() $\mu _n$
-action. Since
$\mu _n$
-action. Since
![]() $H = 0$
in
$H = 0$
in
![]() $\hat {B}$
, we have
$\hat {B}$
, we have
![]() $H_i = 0$
in
$H_i = 0$
in
![]() $\hat {B}$
, and hence there are
$\hat {B}$
, and hence there are
![]() $f_i \in k[[x,y,z]]$
such that
$f_i \in k[[x,y,z]]$
such that
![]() $H_i = f_i H$
. Since
$H_i = f_i H$
. Since
![]() $\sum f_i = 1$
, there exists
$\sum f_i = 1$
, there exists
![]() $d \in \mathbb Z/n\mathbb Z$
with
$d \in \mathbb Z/n\mathbb Z$
with
![]() $f_d \in k[[x,y,z]]^*$
. We can take
$f_d \in k[[x,y,z]]^*$
. We can take
![]() $F = H_d$
, which is of weight d.
$F = H_d$
, which is of weight d.
Then
![]() $H^0(\operatorname {\mathrm {Spec}} \hat {B} \setminus \{\mathfrak {m}\}, \Omega ^2_{\hat {B}/k})$
is generated by
$H^0(\operatorname {\mathrm {Spec}} \hat {B} \setminus \{\mathfrak {m}\}, \Omega ^2_{\hat {B}/k})$
is generated by
![]() $\omega = F_x^{-1} dy \wedge dz = F_y^{-1} dz \wedge dx = F_z^{-1} dx \wedge dy$
(this means that the restriction of
$\omega = F_x^{-1} dy \wedge dz = F_y^{-1} dz \wedge dx = F_z^{-1} dx \wedge dy$
(this means that the restriction of
![]() $\omega $
to the open subscheme
$\omega $
to the open subscheme
![]() $\operatorname {\mathrm {Spec}} \hat {B}[F_x^{-1}]$
is equal to
$\operatorname {\mathrm {Spec}} \hat {B}[F_x^{-1}]$
is equal to
![]() $F_x^{-1} dy \wedge dz$
, and so on), and we have
$F_x^{-1} dy \wedge dz$
, and so on), and we have
![]() $\operatorname {\mathrm {wt}}(\omega ) = a + b + c - d$
since
$\operatorname {\mathrm {wt}}(\omega ) = a + b + c - d$
since
![]() $\operatorname {\mathrm {wt}}(F_x^{-1}) = -(d - a)$
and
$\operatorname {\mathrm {wt}}(F_x^{-1}) = -(d - a)$
and
![]() $\operatorname {\mathrm {wt}}(dy \wedge dz) = b + c$
, and so on.
$\operatorname {\mathrm {wt}}(dy \wedge dz) = b + c$
, and so on.
4.2
 $\mu _p$
-actions on RDPs
$\mu _p$
-actions on RDPs
As noted in §2.3, we know by [Reference Rudakov and ShafarevichS, Prop. 6] (see also [Reference OgusRS, Th. 1 and Corollary]) that the quotient of a smooth variety by a
![]() $\mu _p$
-action with no isolated fixed point is smooth. We need to consider, more generally, the quotients of surfaces with RDP singularities and with isolated fixed points.
$\mu _p$
-action with no isolated fixed point is smooth. We need to consider, more generally, the quotients of surfaces with RDP singularities and with isolated fixed points.
Let
![]() $\mathcal {O}_{X,w}$
and
$\mathcal {O}_{X,w}$
and
![]() $\mu _n$
be as in the beginning of §4, and suppose
$\mu _n$
be as in the beginning of §4, and suppose
![]() $n = p$
. Let
$n = p$
. Let
![]() $\pi \colon X \to Y = X/\mu _p$
be the quotient morphism.
$\pi \colon X \to Y = X/\mu _p$
be the quotient morphism.
Theorem 4.6.
-
1. Assume w is non-fixed. If w is a smooth point, then
 $\pi (w) \in Y$
is also a smooth point. If w is an RDP, then
$\pi (w) \in Y$
is also a smooth point. If w is an RDP, then
 $\pi (w)$
is either a smooth point or an RDP. In either case,
$\pi (w)$
is either a smooth point or an RDP. In either case,
 $X \times _Y \tilde {Y} \to X$
is crepant, where
$X \times _Y \tilde {Y} \to X$
is crepant, where
 $\tilde {Y} \to Y$
is the minimal resolution at
$\tilde {Y} \to Y$
is the minimal resolution at
 $\pi (w)$
.
$\pi (w)$
. -
2. If w is fixed and the action is symplectic at w, then w is an isolated fixed point and
 $\pi (w)$
is an RDP.
$\pi (w)$
is an RDP. -
3. If w is an isolated fixed point and the action is non-symplectic at w, then
 $\pi (w)$
is a non-RDP singularity.
$\pi (w)$
is a non-RDP singularity.
First, we consider non-symplectic actions on isolated fixed points.
Proof of Theorem 4.6(3)
By Proposition 2.10, we have an isomorphism
preserving the zero loci of
![]() $2$
-forms. If
$2$
-forms. If
![]() $\pi (w)$
is either a smooth point or an RDP, then the right-hand side has a nonvanishing
$\pi (w)$
is either a smooth point or an RDP, then the right-hand side has a nonvanishing
![]() $2$
-form and hence there is a nonvanishing form
$2$
-form and hence there is a nonvanishing form
![]() $\omega $
on
$\omega $
on
![]() $\operatorname {\mathrm {Spec}} \mathcal {O}_{X,w} \setminus \{w\}$
of weight
$\operatorname {\mathrm {Spec}} \mathcal {O}_{X,w} \setminus \{w\}$
of weight
![]() $0$
. Being nonvanishing,
$0$
. Being nonvanishing,
![]() $\omega $
is a generator of
$\omega $
is a generator of
![]() $H^0(\operatorname {\mathrm {Spec}} \mathcal {O}_{X,w} \setminus \{w\}, \Omega ^2)$
. However, this contradicts the non-symplecticness assumption.
$H^0(\operatorname {\mathrm {Spec}} \mathcal {O}_{X,w} \setminus \{w\}, \Omega ^2)$
. However, this contradicts the non-symplecticness assumption.
Next, we consider non-fixed points. In fact, we can classify all possible actions and give explicit equations.
Proposition 4.7. Assume w is not fixed.
-
• If w is a smooth point, then there are coordinates
 $x,y$
of
$x,y$
of
 $\mathcal {O}_{X,w}$
satisfying
$\mathcal {O}_{X,w}$
satisfying
 $D(x) = 0$
and
$D(x) = 0$
and
 $D(y) \neq 0$
, and hence
$D(y) \neq 0$
, and hence
 $\mathcal {O}_{Y,\pi (w)}$
has
$\mathcal {O}_{Y,\pi (w)}$
has
 $x,y^p$
as coordinates and in particular
$x,y^p$
as coordinates and in particular
 $\pi (w)$
is a smooth point.
$\pi (w)$
is a smooth point. -
• If w is an RDP, then there is an element
 $F \in k[[x,y,z^p]]$
and an isomorphism
$F \in k[[x,y,z^p]]$
and an isomorphism
 $\hat {\mathcal {O}}_{X,w} \cong k[[x,y,z]] / (F)$
with
$\hat {\mathcal {O}}_{X,w} \cong k[[x,y,z]] / (F)$
with
 $D(x) = D(y) = 0$
and
$D(x) = D(y) = 0$
and
 $D(z) \neq 0$
, and hence
$D(z) \neq 0$
, and hence
 $\hat {\mathcal {O}}_{Y,\pi (w)} \cong k[[x,y,z^p]] / (F)$
. Moreover, we can take F to be one in Table 3.
$\hat {\mathcal {O}}_{Y,\pi (w)} \cong k[[x,y,z^p]] / (F)$
. Moreover, we can take F to be one in Table 3.
Table 3 Non-fixed
![]() $\mu _p$
-actions on RDPs.
$\mu _p$
-actions on RDPs.

Proof of Theorem 4.6(1) and Proposition 4.7
If w is a smooth point, then taking coordinates
![]() $x,y$
as in Lemma 2.9 (i.e.,
$x,y$
as in Lemma 2.9 (i.e.,
![]() $D(x) = 0$
and
$D(x) = 0$
and
![]() $D(y) = 1+y$
), we have
$D(y) = 1+y$
), we have
![]() $\hat {\mathcal {O}}_{Y,\pi (w)} \cong k[[x,y^p]]$
, and hence
$\hat {\mathcal {O}}_{Y,\pi (w)} \cong k[[x,y^p]]$
, and hence
![]() $\mathcal {O}_{Y,\pi (w)}$
is smooth.
$\mathcal {O}_{Y,\pi (w)}$
is smooth.
Assume w is an RDP. By Lemma 2.9, we have coordinates
![]() $x,y,z$
satisfying
$x,y,z$
satisfying
![]() $D(x) = D(y) = 0$
and
$D(x) = D(y) = 0$
and
![]() $D(z) \neq 0$
. We have
$D(z) \neq 0$
. We have
![]() $\hat {\mathcal {O}}_{X,w} \cong k[[x,y,z]] / (F)$
for some
$\hat {\mathcal {O}}_{X,w} \cong k[[x,y,z]] / (F)$
for some
![]() $F \in k[[x,y,z]]$
such that
$F \in k[[x,y,z]]$
such that
![]() $D(F) \in (F)$
, and we may assume
$D(F) \in (F)$
, and we may assume
![]() $F \in k[[x,y,z^p]]$
. We show that, after replacing F with a multiple by a unit, and after a coordinate change of
$F \in k[[x,y,z^p]]$
. We show that, after replacing F with a multiple by a unit, and after a coordinate change of
![]() $k[[x,y,z]]$
that preserves the subring
$k[[x,y,z]]$
that preserves the subring
![]() $k[[x,y,z^p]]$
, F coincides with one in Table 3. (Such coordinate changes are given by
$k[[x,y,z^p]]$
, F coincides with one in Table 3. (Such coordinate changes are given by
![]() $x',y',z' \in \mathfrak {m}$
that are linearly independent in
$x',y',z' \in \mathfrak {m}$
that are linearly independent in
![]() $\mathfrak {m}/\mathfrak {m}^2$
and satisfy
$\mathfrak {m}/\mathfrak {m}^2$
and satisfy
![]() $x',y' \in \mathfrak {m} \cap k[[x,y,z^p]]$
.) A similar classification is given in [Reference Ekedahl, Hyland and Shepherd-BarronEH+, Prop. 3.8], but they missed the case of
$x',y' \in \mathfrak {m} \cap k[[x,y,z^p]]$
.) A similar classification is given in [Reference Ekedahl, Hyland and Shepherd-BarronEH+, Prop. 3.8], but they missed the case of
![]() $E_7^0$
in characteristic
$E_7^0$
in characteristic
![]() $3$
.
$3$
.
Assume the classification for the moment. Then, in each case, we observe that
![]() $\pi (w)$
is either a smooth point or an RDP, and it is straightforward to check that
$\pi (w)$
is either a smooth point or an RDP, and it is straightforward to check that
![]() $X \times _Y \tilde {Y}$
is an RDP surface crepant over X. (In Table 3, the entries of the singularities of
$X \times _Y \tilde {Y}$
is an RDP surface crepant over X. (In Table 3, the entries of the singularities of
![]() $X \times _Y \tilde {Y}$
are omitted if Y is already smooth.) For example, consider
$X \times _Y \tilde {Y}$
are omitted if Y is already smooth.) For example, consider
![]() $X = \operatorname {\mathrm {Spec}} k[x,y,z]/(F)$
,
$X = \operatorname {\mathrm {Spec}} k[x,y,z]/(F)$
,
![]() $F = xy + z^{mp}$
with
$F = xy + z^{mp}$
with
![]() $m \geq 2$
. Then
$m \geq 2$
. Then
![]() $X' := X \times _Y \operatorname {\mathrm {Bl}}_{\pi (w)} Y$
is covered by three affine pieces
$X' := X \times _Y \operatorname {\mathrm {Bl}}_{\pi (w)} Y$
is covered by three affine pieces
 $$ \begin{align*} X^{\prime}_1 &= \operatorname{\mathrm{Spec}} k[x, y_1, v_1, z] / (y_1 + x^{m-2} v_1^{m}, x v_1 - z^p), & y_1 &= y/x, & v_1 &= z^p/x, \\ X^{\prime}_2 &= \operatorname{\mathrm{Spec}} k[x_2, y, v_2, z] / (x_2 + y^{m-2} v_2^{m}, y v_2 - z^p), & x_2 &= x/y, & v_2 &= z^p/y, \\ X^{\prime}_3 &= \operatorname{\mathrm{Spec}} k[x_3, y_3, z] / (x_3 y_3 + z^{(m-2)p}), & x_3 &= x/z^p, & y_3 &= y/z^p. \end{align*} $$
$$ \begin{align*} X^{\prime}_1 &= \operatorname{\mathrm{Spec}} k[x, y_1, v_1, z] / (y_1 + x^{m-2} v_1^{m}, x v_1 - z^p), & y_1 &= y/x, & v_1 &= z^p/x, \\ X^{\prime}_2 &= \operatorname{\mathrm{Spec}} k[x_2, y, v_2, z] / (x_2 + y^{m-2} v_2^{m}, y v_2 - z^p), & x_2 &= x/y, & v_2 &= z^p/y, \\ X^{\prime}_3 &= \operatorname{\mathrm{Spec}} k[x_3, y_3, z] / (x_3 y_3 + z^{(m-2)p}), & x_3 &= x/z^p, & y_3 &= y/z^p. \end{align*} $$
One observes that
![]() $\operatorname {\mathrm {Sing}}(X')$
consists of two RDPs of type
$\operatorname {\mathrm {Sing}}(X')$
consists of two RDPs of type
![]() $A_{p-1}$
at the origins of
$A_{p-1}$
at the origins of
![]() $X^{\prime }_1$
and
$X^{\prime }_1$
and
![]() $X^{\prime }_2$
and, if
$X^{\prime }_2$
and, if
![]() $m \geq 3$
, one RDP of type
$m \geq 3$
, one RDP of type
![]() $A_{(m-2)p-1}$
at the origin of
$A_{(m-2)p-1}$
at the origin of
![]() $X^{\prime }_3$
. Repeating this, we observe that
$X^{\prime }_3$
. Repeating this, we observe that
![]() $X \times _Y \tilde {Y}$
has
$X \times _Y \tilde {Y}$
has
![]() $m A_{p-1}$
.
$m A_{p-1}$
.
Now, we show the classification. We say that F has a monomial if the coefficient of that monomial is nonzero. We also write
![]() $F = \sum _{h,i,j} a_{hij} x^h y^i z^j$
.
$F = \sum _{h,i,j} a_{hij} x^h y^i z^j$
.
First, assume
![]() $p> 2$
. We may assume that the degree
$p> 2$
. We may assume that the degree
![]() $2$
part
$2$
part
![]() $F_2$
is either
$F_2$
is either
![]() $xy$
or
$xy$
or
![]() $x^2$
. Assume
$x^2$
. Assume
![]() $F_2 = xy$
. We may assume that F has no
$F_2 = xy$
. We may assume that F has no
![]() $xz^{j}$
and
$xz^{j}$
and
![]() $yz^{j}$
. F must have
$yz^{j}$
. F must have
![]() $z^{j}$
,
$z^{j}$
,
![]() $j = mp$
, and then it is
$j = mp$
, and then it is
![]() $A_{mp-1}$
. Then, by replacing x with
$A_{mp-1}$
. Then, by replacing x with
![]() $x + a_{0ij} y^{i-1} z^j$
and y with
$x + a_{0ij} y^{i-1} z^j$
and y with
![]() $y + a_{h0j} x^{h-1} z^j$
, and so on, we may assume that F has no
$y + a_{h0j} x^{h-1} z^j$
, and so on, we may assume that F has no
![]() $y^i z^j$
with
$y^i z^j$
with
![]() $i> 0$
and no
$i> 0$
and no
![]() $x^h z^j$
with
$x^h z^j$
with
![]() $h> 0$
. Thus,
$h> 0$
. Thus,
![]() $F = u_1 xy + u_2 z^{mp}$
for some units
$F = u_1 xy + u_2 z^{mp}$
for some units
![]() $u_1, u_2$
, and then by replacing
$u_1, u_2$
, and then by replacing
![]() $x,y,F$
by suitable multiples, we obtain
$x,y,F$
by suitable multiples, we obtain
![]() $F = xy + z^{mp}$
.
$F = xy + z^{mp}$
.
Assume
![]() $p> 3$
and
$p> 3$
and
![]() $F_2 = x^2$
. We may assume that the degree
$F_2 = x^2$
. We may assume that the degree
![]() $3$
part
$3$
part
![]() $F_3$
is
$F_3$
is
![]() $y^3$
. If
$y^3$
. If
![]() $p \geq 7$
, it cannot be an RDP. If
$p \geq 7$
, it cannot be an RDP. If
![]() $p = 5$
, then F must have
$p = 5$
, then F must have
![]() $z^5$
, and then it is
$z^5$
, and then it is
![]() $E_8^0$
. We have
$E_8^0$
. We have
![]() $F = u_1 x^2 + u_2 y^3 + u_3 z^5$
, and then by replacing
$F = u_1 x^2 + u_2 y^3 + u_3 z^5$
, and then by replacing
![]() $x,y,F$
by suitable multiples, we obtain
$x,y,F$
by suitable multiples, we obtain
![]() $F = x^2 + y^3 + z^5$
. (For example, we let
$F = x^2 + y^3 + z^5$
. (For example, we let
![]() $F = u_3 F'$
,
$F = u_3 F'$
,
![]() $x = (u_3 u_1^{-1})^{1/2} x'$
,
$x = (u_3 u_1^{-1})^{1/2} x'$
,
![]() $y = (u_3 u_2^{-1})^{1/3} y'$
. Note that we can take nth roots of units provided
$y = (u_3 u_2^{-1})^{1/3} y'$
. Note that we can take nth roots of units provided
![]() $p \nmid n$
.)
$p \nmid n$
.)
Assume
![]() $p = 3$
and
$p = 3$
and
![]() $F_2 = x^2$
. We may assume
$F_2 = x^2$
. We may assume
![]() $F_3 = y^3$
or
$F_3 = y^3$
or
![]() $F_3 = z^3$
. If
$F_3 = z^3$
. If
![]() $F_3 = z^3$
, then F must have
$F_3 = z^3$
, then F must have
![]() $y^4$
or
$y^4$
or
![]() $y^5$
, and then it is
$y^5$
, and then it is
![]() $E_6^0$
or
$E_6^0$
or
![]() $E_8^0$
. We may assume
$E_8^0$
. We may assume
![]() $a_{130} = a_{140} = 0$
by replacing x with
$a_{130} = a_{140} = 0$
by replacing x with
![]() $x + (1/2)(a_{130} y^3 + a_{140} y^4)$
, and then we transform F as above. If
$x + (1/2)(a_{130} y^3 + a_{140} y^4)$
, and then we transform F as above. If
![]() $F_3 = y^3$
, then F must have
$F_3 = y^3$
, then F must have
![]() $yz^3$
and then it is
$yz^3$
and then it is
![]() $E_7^0$
. We eliminate
$E_7^0$
. We eliminate
![]() $a_{1ij}$
as above, then we have
$a_{1ij}$
as above, then we have
![]() $F = u_1 x^2 + u_2 y^3 + u_3 yz^3 + z^6 g(z^3)$
for some power series
$F = u_1 x^2 + u_2 y^3 + u_3 yz^3 + z^6 g(z^3)$
for some power series
![]() $g \in k[[z^3]]$
. We may assume
$g \in k[[z^3]]$
. We may assume
![]() $u_i \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate g by replacing y with
$u_i \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate g by replacing y with
![]() $y + z^3 g$
, and then we transform F as above.
$y + z^3 g$
, and then we transform F as above.
Now, consider
![]() $p = 2$
. We may assume
$p = 2$
. We may assume
![]() $F_2$
is one of
$F_2$
is one of
![]() $xy + z^2$
(if irreducible),
$xy + z^2$
(if irreducible),
![]() $xy$
(if reducible but not a square),
$xy$
(if reducible but not a square),
![]() $z^2$
, or
$z^2$
, or
![]() $x^2$
(square, of a linear factor containing z or not). If
$x^2$
(square, of a linear factor containing z or not). If
![]() $F_2 = xy + z^2$
or
$F_2 = xy + z^2$
or
![]() $F_2 = xy$
, then as above, it is
$F_2 = xy$
, then as above, it is
![]() $A_{mp-1}$
and F becomes
$A_{mp-1}$
and F becomes
![]() $xy + z^{mp}$
.
$xy + z^{mp}$
.
Assume
![]() $p = 2$
and
$p = 2$
and
![]() $F_2 = x^2$
. If
$F_2 = x^2$
. If
![]() $F_3$
has
$F_3$
has
![]() $yz^2$
, then F must have
$yz^2$
, then F must have
![]() $xy^m$
and then it is
$xy^m$
and then it is
![]() $D_{2m+1}^0$
. We obtain
$D_{2m+1}^0$
. We obtain
![]() $F = u_1 x^2 + u_2 y z^2 + u_3 x y^m + z^4 g(z) + f(y) + y^{2m} g'(y)$
, where
$F = u_1 x^2 + u_2 y z^2 + u_3 x y^m + z^4 g(z) + f(y) + y^{2m} g'(y)$
, where
![]() $f(y) = f_0(y)^2 + y f_1(y)^2$
is a polynomial of degree
$f(y) = f_0(y)^2 + y f_1(y)^2$
is a polynomial of degree
![]() $< 2m$
,
$< 2m$
,
![]() $g(z) \in k[[z]]$
, and
$g(z) \in k[[z]]$
, and
![]() $g'(y) \in k[[y]]$
. We may assume
$g'(y) \in k[[y]]$
. We may assume
![]() $u_i \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate f by replacing x with
$u_i \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate f by replacing x with
![]() $x + f_0(y)$
and z with
$x + f_0(y)$
and z with
![]() $z + f_1(y)$
and so on. Then we eliminate g and
$z + f_1(y)$
and so on. Then we eliminate g and
![]() $g'$
by replacing y and x suitably, and take multiples by units as above.
$g'$
by replacing y and x suitably, and take multiples by units as above.
If
![]() $F_3$
has no
$F_3$
has no
![]() $yz^2$
, then F must have
$yz^2$
, then F must have
![]() $y^3$
and
$y^3$
and
![]() $xz^2$
and then it is
$xz^2$
and then it is
![]() $E_6^0$
. We obtain
$E_6^0$
. We obtain
![]() $F = u_1 x^2 + u_2 y^3 + u_3 x z^2 + a y^2 z^2 + z^4 g$
,
$F = u_1 x^2 + u_2 y^3 + u_3 x z^2 + a y^2 z^2 + z^4 g$
,
![]() $g = g_0(z^2) + y g_1(z^2) + y^2 g_2(z^2)$
. We may assume
$g = g_0(z^2) + y g_1(z^2) + y^2 g_2(z^2)$
. We may assume
![]() $u_i \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate a and g by replacing y and x suitably, and then we transform F as above.
$u_i \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate a and g by replacing y and x suitably, and then we transform F as above.
Assume
![]() $p = 2$
and
$p = 2$
and
![]() $F_2 = z^2$
. Let
$F_2 = z^2$
. Let
![]() $\overline {F_3} = (F_3 \bmod (z)) \in k[[x,y]]$
. If
$\overline {F_3} = (F_3 \bmod (z)) \in k[[x,y]]$
. If
![]() $\overline {F_3}$
has three distinct roots, then we may assume
$\overline {F_3}$
has three distinct roots, then we may assume
![]() $\overline {F_3} = x^3 + y^3$
and then it is
$\overline {F_3} = x^3 + y^3$
and then it is
![]() $D_4^0$
. We can transform F to
$D_4^0$
. We can transform F to
![]() $z^2 + x^3 + y^3$
as above, and then to
$z^2 + x^3 + y^3$
as above, and then to
![]() $z^2 + x^2 y + x y^2$
. If
$z^2 + x^2 y + x y^2$
. If
![]() $\overline {F_3}$
has two distinct roots, then we may assume
$\overline {F_3}$
has two distinct roots, then we may assume
![]() $\overline {F_3} = x^2y$
and F must have
$\overline {F_3} = x^2y$
and F must have
![]() $xy^m$
and then it is
$xy^m$
and then it is
![]() $D_{2m}^0$
. We obtain
$D_{2m}^0$
. We obtain
![]() $F = u_1 z^2 + u_2 x^2 y + u_3 x y^m + g(x) + f(y) + y^{2m-1} g'(y)$
, where
$F = u_1 z^2 + u_2 x^2 y + u_3 x y^m + g(x) + f(y) + y^{2m-1} g'(y)$
, where
![]() $f(y) = f_0(y)^2 + y f_1(y)^2$
is a polynomial of degree
$f(y) = f_0(y)^2 + y f_1(y)^2$
is a polynomial of degree
![]() $< 2m-1$
and
$< 2m-1$
and
![]() $g \in k[[x]]$
and
$g \in k[[x]]$
and
![]() $g' \in k[[y]]$
. We argue as in the case of
$g' \in k[[y]]$
. We argue as in the case of
![]() $D_{2m+1}^0$
. If
$D_{2m+1}^0$
. If
![]() $\overline {F_3}$
has one (triple) root, then we may assume
$\overline {F_3}$
has one (triple) root, then we may assume
![]() $\overline {F_3} = x^3$
and F must have
$\overline {F_3} = x^3$
and F must have
![]() $xy^3$
or
$xy^3$
or
![]() $y^5$
and then it is
$y^5$
and then it is
![]() $E_7^0$
or
$E_7^0$
or
![]() $E_8^0$
. We transform F as above.
$E_8^0$
. We transform F as above.
Next, we consider symplectic actions on fixed points.
Lemma 4.8. Assume w is fixed, and the action is symplectic at w.
-
1. Assume w is a smooth point. Then w is an isolated fixed point and
 $\pi (w)$
is an RDP of type
$\pi (w)$
is an RDP of type
 $A_{p-1}$
. The eigenvalues of D on the cotangent space
$A_{p-1}$
. The eigenvalues of D on the cotangent space
 $\mathfrak {m}_w / \mathfrak {m}_w^2$
are of the form
$\mathfrak {m}_w / \mathfrak {m}_w^2$
are of the form
 $a,-a$
for some
$a,-a$
for some
 $a \in \mathbb F_p^*$
.
$a \in \mathbb F_p^*$
. -
2. Assume w is an RDP. Let
 ${f}:{X' = \operatorname {\mathrm {Bl}}_w X}\to {X}$
. Then
${f}:{X' = \operatorname {\mathrm {Bl}}_w X}\to {X}$
. Then
 $X'$
is an RDP surface, D uniquely extends to a derivation
$X'$
is an RDP surface, D uniquely extends to a derivation
 $D'$
on
$D'$
on
 $X'$
which is symplectic at every fixed point above w, and
$X'$
which is symplectic at every fixed point above w, and
 $g \colon Y' = (X')^{D'} \to Y$
is crepant.
$g \colon Y' = (X')^{D'} \to Y$
is crepant.
Proof. (1) By Lemma 4.5(1), we have
![]() $D = a x \cdot (\partial / \partial x) - a y \cdot (\partial / \partial y)$
with
$D = a x \cdot (\partial / \partial x) - a y \cdot (\partial / \partial y)$
with
![]() $a \in \mathbb F_p$
for some coordinates
$a \in \mathbb F_p$
for some coordinates
![]() $x,y$
, and
$x,y$
, and
![]() $a \neq 0$
since D is nontrivial. Hence, w is an isolated fixed point of D. We observe that
$a \neq 0$
since D is nontrivial. Hence, w is an isolated fixed point of D. We observe that
![]() $a,-a$
are the eigenvalues of the action on the cotangent space. We have
$a,-a$
are the eigenvalues of the action on the cotangent space. We have
![]() $\hat {\mathcal {O}}_{X,w}^D = k[[x^p, xy, y^p]]$
, and it is an RDP of type
$\hat {\mathcal {O}}_{X,w}^D = k[[x^p, xy, y^p]]$
, and it is an RDP of type
![]() $A_{p-1}$
.
$A_{p-1}$
.
(2) By Remark 4.3 and assertion (1), w is an isolated fixed point. By Proposition 2.8, D uniquely extends to
![]() $D'$
on
$D'$
on
![]() $X'$
. Let
$X'$
. Let
![]() $\omega $
be a generator of
$\omega $
be a generator of
![]() $H^0(\operatorname {\mathrm {Spec}} \mathcal {O}_{X,w} \setminus \{w\}, \Omega ^2)$
with
$H^0(\operatorname {\mathrm {Spec}} \mathcal {O}_{X,w} \setminus \{w\}, \Omega ^2)$
with
![]() $D(\omega ) = 0$
. Since w is an RDP,
$D(\omega ) = 0$
. Since w is an RDP,
![]() $X'$
is again an RDP surface, and it follows from Proposition 2.3 that
$X'$
is again an RDP surface, and it follows from Proposition 2.3 that
![]() $\omega $
extends to
$\omega $
extends to
![]() $\omega '$
on
$\omega '$
on
![]() $(X')^{\mathrm {sm}}$
, which generates
$(X')^{\mathrm {sm}}$
, which generates
![]() $H^0(\operatorname {\mathrm {Spec}} \mathcal {O}_{X',w'} \setminus \{w'\}, \Omega ^2)$
at any closed point
$H^0(\operatorname {\mathrm {Spec}} \mathcal {O}_{X',w'} \setminus \{w'\}, \Omega ^2)$
at any closed point
![]() $w' \in X'$
above w, and that
$w' \in X'$
above w, and that
![]() $D'(\omega ') = 0$
. Hence,
$D'(\omega ') = 0$
. Hence,
![]() $D'$
is symplectic at every fixed point above w. Since as above such fixed points are isolated,
$D'$
is symplectic at every fixed point above w. Since as above such fixed points are isolated,
![]() $Y'$
is smooth outside finitely many isolated points. Applying Proposition 2.10 to
$Y'$
is smooth outside finitely many isolated points. Applying Proposition 2.10 to
![]() $\omega $
on
$\omega $
on
![]() $X \setminus \{w\}$
and
$X \setminus \{w\}$
and
![]() $\omega '$
on
$\omega '$
on
![]() $X' \setminus (\operatorname {\mathrm {Sing}}(X') \cup \operatorname {\mathrm {Fix}}(D'))$
, we obtain
$X' \setminus (\operatorname {\mathrm {Sing}}(X') \cup \operatorname {\mathrm {Fix}}(D'))$
, we obtain
![]() $2$
-forms
$2$
-forms
![]() $\psi $
on
$\psi $
on
![]() $Y \setminus \{\pi (w)\}$
and
$Y \setminus \{\pi (w)\}$
and
![]() $\psi '$
on
$\psi '$
on
![]() $Y' \setminus \pi ((\operatorname {\mathrm {Sing}}(X') \cup \operatorname {\mathrm {Fix}}(D')))$
, which are nonvanishing. Comparing
$Y' \setminus \pi ((\operatorname {\mathrm {Sing}}(X') \cup \operatorname {\mathrm {Fix}}(D')))$
, which are nonvanishing. Comparing
![]() $\psi $
and
$\psi $
and
![]() $\psi '$
, we observe that g is crepant.
$\psi '$
, we observe that g is crepant.
Proof of Theorem 4.6(2)
By Remark 4.3 and Lemma 4.8(1), w is an isolated fixed point. By shrinking X, we may assume that D has no fixed point except w.
We construct a finite sequence
![]() $(X_j,D_j)_{0 \leq j \leq n}$
(
$(X_j,D_j)_{0 \leq j \leq n}$
(
![]() $n \geq 0$
) of RDP surfaces
$n \geq 0$
) of RDP surfaces
![]() $X_j$
and derivations
$X_j$
and derivations
![]() $D_j$
on
$D_j$
on
![]() $X_j$
of multiplicative type that is symplectic at each fixed point. Let
$X_j$
of multiplicative type that is symplectic at each fixed point. Let
![]() $(X_0,D_0) = (X,D)$
. If
$(X_0,D_0) = (X,D)$
. If
![]() $X_j$
has no fixed RDP, then we terminate the sequence at
$X_j$
has no fixed RDP, then we terminate the sequence at
![]() $n = j$
. If
$n = j$
. If
![]() $X_j$
has at least one fixed RDP, let
$X_j$
has at least one fixed RDP, let
![]() $X_{j+1}$
be the blowup of
$X_{j+1}$
be the blowup of
![]() $X_j$
at the fixed RDPs and
$X_j$
at the fixed RDPs and
![]() $D_{j+1}$
the extension of
$D_{j+1}$
the extension of
![]() $D_j$
to
$D_j$
to
![]() $X_{j+1}$
. Since any RDP becomes smooth after a finite number of blowups at RDPs, this sequence terminates at some
$X_{j+1}$
. Since any RDP becomes smooth after a finite number of blowups at RDPs, this sequence terminates at some
![]() $n \geq 0$
. By Lemma 4.8(2),
$n \geq 0$
. By Lemma 4.8(2),
![]() $D_{j+1}$
on
$D_{j+1}$
on
![]() $X_{j+1}$
is symplectic at each fixed point, and
$X_{j+1}$
is symplectic at each fixed point, and
![]() $(X_{j+1})^{D_{j+1}} \to (X_j)^{D_j}$
is crepant. By Theorem 4.6(1) and Lemma 4.8(1),
$(X_{j+1})^{D_{j+1}} \to (X_j)^{D_j}$
is crepant. By Theorem 4.6(1) and Lemma 4.8(1),
![]() $Y_n = (X_n)^{D_n}$
has canonical singularity (i.e., has no singularity other than RDPs), and since
$Y_n = (X_n)^{D_n}$
has canonical singularity (i.e., has no singularity other than RDPs), and since
![]() $Y_n \to Y = X^D$
is crepant, also Y has canonical singularity. If
$Y_n \to Y = X^D$
is crepant, also Y has canonical singularity. If
![]() $n> 0$
, then
$n> 0$
, then
![]() $\pi (w)$
is not a smooth point since
$\pi (w)$
is not a smooth point since
![]() $Y_n \to Y$
is a crepant morphism non-isomorphic at that point, and if
$Y_n \to Y$
is a crepant morphism non-isomorphic at that point, and if
![]() $n = 0$
, then
$n = 0$
, then
![]() $\pi (w)$
is not a smooth point by Lemma 4.8(1). Hence, in either case,
$\pi (w)$
is not a smooth point by Lemma 4.8(1). Hence, in either case,
![]() $\pi (w)$
is an RDP.
$\pi (w)$
is an RDP.
Moreover, we can classify all possible symplectic
![]() $\mu _p$
-actions on RDPs.
$\mu _p$
-actions on RDPs.
Proposition 4.9. Assume w is a fixed RDP, and the action is symplectic at w. Then there is a
![]() $\mu _p$
-equivariant isomorphism
$\mu _p$
-equivariant isomorphism
![]() $\hat {\mathcal {O}}_{X,w} \cong k[[x,y,z]]/(F)$
with F equal to one in Table 4 and
$\hat {\mathcal {O}}_{X,w} \cong k[[x,y,z]]/(F)$
with F equal to one in Table 4 and
![]() $\mu _p$
acts on
$\mu _p$
acts on
![]() $x,y,z$
by respective weights
$x,y,z$
by respective weights
![]() $a,-a,0$
for some
$a,-a,0$
for some
![]() $a \in \mathbb F_p^*$
. The singularities of X,
$a \in \mathbb F_p^*$
. The singularities of X,
![]() $X' = \operatorname {\mathrm {Bl}}_w X$
,
$X' = \operatorname {\mathrm {Bl}}_w X$
,
![]() $X/\mu _p$
, and
$X/\mu _p$
, and
![]() $X'/\mu _p$
are displayed in the table.
$X'/\mu _p$
are displayed in the table.
Table 4 Symplectic
![]() $\mu _p$
-actions on RDPs.
$\mu _p$
-actions on RDPs.

![]() $\bullet \ A_0$
is a smooth point that is an isolated fixed point of D.
$\bullet \ A_0$
is a smooth point that is an isolated fixed point of D.
![]() $\bullet \ [\mathsf {n}]$
means that the RDP is not fixed by D.
$\bullet \ [\mathsf {n}]$
means that the RDP is not fixed by D.
![]() $\bullet \ \lfloor q \rfloor := \max \{n \in \mathbb Z \mid n \leq q\}$
denotes the integer part of a real q.
$\bullet \ \lfloor q \rfloor := \max \{n \in \mathbb Z \mid n \leq q\}$
denotes the integer part of a real q.
![]() $\bullet \ q^+ := \max \{q,0\}$
denotes the positive part of a real q.
$\bullet \ q^+ := \max \{q,0\}$
denotes the positive part of a real q.
![]() $\bullet \ [*]$
: It follows from the classification that for each (formal) isomorphism class of RDP, there
$\bullet \ [*]$
: It follows from the classification that for each (formal) isomorphism class of RDP, there
exists only one fixed symplectic
![]() $\mu _p$
-action up to isomorphism, except for the case of
$\mu _p$
-action up to isomorphism, except for the case of
![]() $D_{2n}^{n-1}$
(
$D_{2n}^{n-1}$
(
![]() $n \geq 3$
)
$n \geq 3$
)
in
![]() $p = 2$
, in which case there are two and they are distinguished by the degree
$p = 2$
, in which case there are two and they are distinguished by the degree
![]() $2$
part
$2$
part
![]() $F_2$
being a
$F_2$
being a
square of a homogeneous element or not. We distinguish them by notation
![]() $D_{2n}^{n-1}$
and
$D_{2n}^{n-1}$
and
![]() $D_{2n}^{n-1}[*]$
. We
$D_{2n}^{n-1}[*]$
. We
use the convention that
![]() $D_4^{1}[*] = D_4^{1}$
.
$D_4^{1}[*] = D_4^{1}$
.
Remark 4.10. A polynomial
![]() $f \in k[x_1, \dots , x_m]$
is called quasi-homogeneous if, for some
$f \in k[x_1, \dots , x_m]$
is called quasi-homogeneous if, for some
![]() $a_1, \dots , a_m \in \mathbb Z_{\geq 1}$
, the monomials appearing in f have the same degree with respect to a (i.e., degree of the monomial
$a_1, \dots , a_m \in \mathbb Z_{\geq 1}$
, the monomials appearing in f have the same degree with respect to a (i.e., degree of the monomial
![]() $x_1^{i_1} \dots x_m^{i_m}$
is
$x_1^{i_1} \dots x_m^{i_m}$
is
![]() $i_1 a_1 + \dots + i_m a_m$
). RDPs whose completions are not defined by quasi-homogeneous polynomials, which exist only if
$i_1 a_1 + \dots + i_m a_m$
). RDPs whose completions are not defined by quasi-homogeneous polynomials, which exist only if
![]() $p = 2,3,5$
, are precisely
$p = 2,3,5$
, are precisely
![]() $D_n^r$
and
$D_n^r$
and
![]() $E_n^r$
with
$E_n^r$
with
![]() $r \neq 0$
. It follows from the classification given in Proposition 4.9 (resp. given in Proposition 4.7, resp. which is omitted) that if an RDP of type
$r \neq 0$
. It follows from the classification given in Proposition 4.9 (resp. given in Proposition 4.7, resp. which is omitted) that if an RDP of type
![]() $D_n$
or
$D_n$
or
![]() $E_n$
admits a fixed symplectic (resp. non-fixed, resp. fixed non-symplectic)
$E_n$
admits a fixed symplectic (resp. non-fixed, resp. fixed non-symplectic)
![]() $\mu _p$
-action, then the singularity is not defined (resp. is defined, resp. is defined) by a quasi-homogeneous polynomial. We do not know any explanation of this phenomenon.
$\mu _p$
-action, then the singularity is not defined (resp. is defined, resp. is defined) by a quasi-homogeneous polynomial. We do not know any explanation of this phenomenon.
Proof of Proposition 4.9
We consider tuples
![]() $(a,b,c,F)$
with
$(a,b,c,F)$
with
![]() $a,b,c \in \mathbb F_p$
, not all
$a,b,c \in \mathbb F_p$
, not all
![]() $0$
, and
$0$
, and
![]() $F \in k[[x,y,z]]$
such that
$F \in k[[x,y,z]]$
such that
![]() $F = 0$
defines an RDP and only monomials of weight
$F = 0$
defines an RDP and only monomials of weight
![]() $a+b+c$
(
$a+b+c$
(
![]() $\in \mathbb F_p$
) appear in F, where
$\in \mathbb F_p$
) appear in F, where
![]() $x,y,z$
have respective weights
$x,y,z$
have respective weights
![]() $a,b,c$
. By Lemma 4.5(2), it suffices to consider
$a,b,c$
. By Lemma 4.5(2), it suffices to consider
![]() $k[[x,y,z]]/(F)$
of this form. We show that there exist a
$k[[x,y,z]]/(F)$
of this form. We show that there exist a
![]() $\mu _p$
-equivariant isomorphism
$\mu _p$
-equivariant isomorphism
![]() $k[[x,y,z]]/(F) \cong k[[x',y',z']]/(F')$
with
$k[[x,y,z]]/(F) \cong k[[x',y',z']]/(F')$
with
![]() $F'$
in Table 4 and
$F'$
in Table 4 and
![]() $\operatorname {\mathrm {wt}}(x',y',z') = (1,-1,0)$
up to
$\operatorname {\mathrm {wt}}(x',y',z') = (1,-1,0)$
up to
![]() $\operatorname {\mathrm {Aut}}(\mu _p) = \mathbb F_p^*$
(which amounts to replacing
$\operatorname {\mathrm {Aut}}(\mu _p) = \mathbb F_p^*$
(which amounts to replacing
![]() $(a,b,c)$
with
$(a,b,c)$
with
![]() $(ta,tb,tc)$
for some
$(ta,tb,tc)$
for some
![]() $t \in \mathbb F_p^*$
).
$t \in \mathbb F_p^*$
).
We write
![]() $F = \sum _{h,i,j} a_{hij} x^h y^i z^j$
, and we say that a polynomial or a formal power series has a monomial if its coefficient is nonzero.
$F = \sum _{h,i,j} a_{hij} x^h y^i z^j$
, and we say that a polynomial or a formal power series has a monomial if its coefficient is nonzero.
First, assume the degree
![]() $2$
part
$2$
part
![]() $F_2$
is a non-square. Then we may assume that
$F_2$
is a non-square. Then we may assume that
![]() $F_2$
contains a non-square monomial, say
$F_2$
contains a non-square monomial, say
![]() $xy$
. (Indeed, if this is not the case, then
$xy$
. (Indeed, if this is not the case, then
![]() $p \neq 2$
and
$p \neq 2$
and
![]() $F_2$
contains at least two square monomials, say
$F_2$
contains at least two square monomials, say
![]() $x^2$
and
$x^2$
and
![]() $y^2$
, then x and y has the same weight, and then after a linear coordinate change, we may assume
$y^2$
, then x and y has the same weight, and then after a linear coordinate change, we may assume
![]() $F_2$
contains
$F_2$
contains
![]() $xy$
.) Then we have
$xy$
.) Then we have
![]() $c = 0$
. If
$c = 0$
. If
![]() $a + b \not \in \{0,a,b\}$
, then
$a + b \not \in \{0,a,b\}$
, then
![]() $F \in (x,y)^2$
, which implies that
$F \in (x,y)^2$
, which implies that
![]() $F = 0$
is not an RDP. If
$F = 0$
is not an RDP. If
![]() $a + b = a \neq 0$
, then
$a + b = a \neq 0$
, then
![]() $F \in (x)$
, again not an RDP. The same if
$F \in (x)$
, again not an RDP. The same if
![]() $a + b = b \neq 0$
. So we have
$a + b = b \neq 0$
. So we have
![]() $a + b = 0$
and hence
$a + b = 0$
and hence
![]() $F \in k[[x^p,xy,y^p,z]]$
. Since F cannot belong to
$F \in k[[x^p,xy,y^p,z]]$
. Since F cannot belong to
![]() $(x,y)$
, there exists an integer m such that F has the monomial
$(x,y)$
, there exists an integer m such that F has the monomial
![]() $z^{m}$
. Let m be the smallest such integer. We have
$z^{m}$
. Let m be the smallest such integer. We have
![]() $F = u_1 z^m + u_2 xy + g_1(x^p) + g_2(y^p)$
for some units
$F = u_1 z^m + u_2 xy + g_1(x^p) + g_2(y^p)$
for some units
![]() $u_1,u_2 \in k[[x^p, x y, y^p, z]]^*$
and power series
$u_1,u_2 \in k[[x^p, x y, y^p, z]]^*$
and power series
![]() $g_1, g_2$
. We may assume
$g_1, g_2$
. We may assume
![]() $u_1,u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate
$u_1,u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We eliminate
![]() $g_1, g_2$
by replacing x with
$g_1, g_2$
by replacing x with
![]() $x + g_2/y$
and y with
$x + g_2/y$
and y with
![]() $y + g_1/x$
(and repeating this), and we obtain
$y + g_1/x$
(and repeating this), and we obtain
![]() $F = u_1 z^m + u_2 xy$
. By replacing
$F = u_1 z^m + u_2 xy$
. By replacing
![]() $x,y,z,F$
with suitable multiples, we obtain
$x,y,z,F$
with suitable multiples, we obtain
![]() $F = z^m + xy$
.
$F = z^m + xy$
.
Next, assume
![]() $p \geq 3$
and
$p \geq 3$
and
![]() $F_2$
is square. We may assume
$F_2$
is square. We may assume
![]() $F_2 = z^2$
. We may assume
$F_2 = z^2$
. We may assume
![]() $F_3 \not \equiv 0 \pmod {z}$
. If
$F_3 \not \equiv 0 \pmod {z}$
. If
![]() $F_3$
has
$F_3$
has
![]() $x^2y$
, then by
$x^2y$
, then by
![]() $2c = 2a + b = a + b + c$
, we have
$2c = 2a + b = a + b + c$
, we have
![]() $b = 0$
and
$b = 0$
and
![]() $a = c$
, and hence
$a = c$
, and hence
![]() $F \in (x,z)^2$
, which is absurd. Hence, we may assume
$F \in (x,z)^2$
, which is absurd. Hence, we may assume
![]() $F_3$
has
$F_3$
has
![]() $y^3$
. By
$y^3$
. By
![]() $2c = 3b = a+b+c$
, we have
$2c = 3b = a+b+c$
, we have
![]() $(a,b,c) = (a,2a,3a)$
. If F does not have
$(a,b,c) = (a,2a,3a)$
. If F does not have
![]() $x^3$
, then
$x^3$
, then
![]() $F \in (z^2, x^3z, xyz, x^6, x^4y, x^2y^2, y^3)$
, and
$F \in (z^2, x^3z, xyz, x^6, x^4y, x^2y^2, y^3)$
, and
![]() $F = 0$
cannot define an RDP. Hence, F has
$F = 0$
cannot define an RDP. Hence, F has
![]() $x^3$
, hence
$x^3$
, hence
![]() $p = 3$
, and then
$p = 3$
, and then
![]() $F \in k[[x^3,xy,y^3,z]]$
. We may assume that F does not have
$F \in k[[x^3,xy,y^3,z]]$
. We may assume that F does not have
![]() $xyz$
. To define an RDP, F must have one of
$xyz$
. To define an RDP, F must have one of
![]() $x^2y^2, x^4y, xy^4$
.
$x^2y^2, x^4y, xy^4$
.
If it has
![]() $x^2y^2$
, then it is
$x^2y^2$
, then it is
![]() $E_6^1$
. We can eliminate
$E_6^1$
. We can eliminate
![]() $x^h y^i z$
, and we have
$x^h y^i z$
, and we have
 $$ \begin{align*} F &= z^2 u_1 + x^3 + y^3 + x^2 y^2 u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ &\qquad S_1 = \{(4,1,0), (1,4,0)\}, \qquad S_2 = \{(6,0), (7,1)\}, \qquad S_3 = \{(0,6), (1,7)\}, \end{align*} $$
$$ \begin{align*} F &= z^2 u_1 + x^3 + y^3 + x^2 y^2 u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ &\qquad S_1 = \{(4,1,0), (1,4,0)\}, \qquad S_2 = \{(6,0), (7,1)\}, \qquad S_3 = \{(0,6), (1,7)\}, \end{align*} $$
where
![]() $a_{hij} \in k$
,
$a_{hij} \in k$
,
![]() $b_{hi} \in k[[x^3]]$
,
$b_{hi} \in k[[x^3]]$
,
![]() $c_{hi} \in k[[y^3]]$
, and
$c_{hi} \in k[[y^3]]$
, and
![]() $u_1, u_2 \in k[[x^3, x y, y^3, z]]^*$
. By replacing x with
$u_1, u_2 \in k[[x^3, x y, y^3, z]]^*$
. By replacing x with
![]() $x + t y^2$
and y with
$x + t y^2$
and y with
![]() $y + t' x^2$
, we eliminate
$y + t' x^2$
, we eliminate
![]() $a_{410}$
and
$a_{410}$
and
![]() $a_{140}$
. Then, by replacing F with
$a_{140}$
. Then, by replacing F with
![]() $(1 + x^3 b_{60} + x^4 y b_{71} + y^3 c_{06} + x y^4 c_{17}) F$
, we eliminate all
$(1 + x^3 b_{60} + x^4 y b_{71} + y^3 c_{06} + x y^4 c_{17}) F$
, we eliminate all
![]() $b_{hi}$
and
$b_{hi}$
and
![]() $c_{hi}$
. Finally, we replace
$c_{hi}$
. Finally, we replace
![]() $x,y,z,F$
with suitable multiples and achieve
$x,y,z,F$
with suitable multiples and achieve
![]() $u_1 = u_2 = 1$
. (For example, we let
$u_1 = u_2 = 1$
. (For example, we let
![]() $F = u_2^{-3} F'$
,
$F = u_2^{-3} F'$
,
![]() $x = u_2^{-1} x'$
,
$x = u_2^{-1} x'$
,
![]() $y = u_2^{-1} y'$
, and
$y = u_2^{-1} y'$
, and
![]() $z = (u_1 u_2^3)^{-1/2} z'$
.)
$z = (u_1 u_2^3)^{-1/2} z'$
.)
If it does not have
![]() $x^2 y^2$
but has
$x^2 y^2$
but has
![]() $x^4 y$
or
$x^4 y$
or
![]() $x y^4$
, then it is
$x y^4$
, then it is
![]() $E_8^1$
. By replacing F with a unit multiple, we may assume that it has
$E_8^1$
. By replacing F with a unit multiple, we may assume that it has
![]() $x^4 y$
and does not have
$x^4 y$
and does not have
![]() $x y^4$
. We can eliminate
$x y^4$
. We can eliminate
![]() $x^h y^i z$
, and we have
$x^h y^i z$
, and we have
 $$ \begin{align*} &F = z^2 u_1 + x^3 + y^3 + x^4 y u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ S_1 &= \{(6,0,0), (3,3,0), (0,6,0)\}, \qquad S_2 = \{(9,0)\}, \qquad S_3 = \{(0,9), (1,7), (2,5), (3,6)\}, \end{align*} $$
$$ \begin{align*} &F = z^2 u_1 + x^3 + y^3 + x^4 y u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ S_1 &= \{(6,0,0), (3,3,0), (0,6,0)\}, \qquad S_2 = \{(9,0)\}, \qquad S_3 = \{(0,9), (1,7), (2,5), (3,6)\}, \end{align*} $$
with
![]() $a_{hij}$
,
$a_{hij}$
,
![]() $b_{hi}$
,
$b_{hi}$
,
![]() $c_{hi}$
, and
$c_{hi}$
, and
![]() $u_1,u_2$
as in the previous case. By replacing y with
$u_1,u_2$
as in the previous case. By replacing y with
![]() $y + t x^2$
, we eliminate
$y + t x^2$
, we eliminate
![]() $a_{600}$
. By replacing x with
$a_{600}$
. By replacing x with
![]() $x + t' y^2$
and F with
$x + t' y^2$
and F with
![]() $(1 + t" y^3) F$
, we eliminate
$(1 + t" y^3) F$
, we eliminate
![]() $a_{330}$
and
$a_{330}$
and
![]() $a_{060}$
. By replacing F with
$a_{060}$
. By replacing F with
![]() $(1 + x^2 y^2 c_{25} + x y^4 c_{17} + y^6 c_{09}) F$
, then with
$(1 + x^2 y^2 c_{25} + x y^4 c_{17} + y^6 c_{09}) F$
, then with
![]() $(1 + x^6 b_{90} + x^3 y^3 c_{36}) F$
, we eliminate all
$(1 + x^6 b_{90} + x^3 y^3 c_{36}) F$
, we eliminate all
![]() $b_{hi}$
and
$b_{hi}$
and
![]() $c_{hi}$
. We replace
$c_{hi}$
. We replace
![]() $x,y,z,F$
with suitable multiples and achieve
$x,y,z,F$
with suitable multiples and achieve
![]() $u_1 = u_2 = 1$
.
$u_1 = u_2 = 1$
.
Hereafter, assume
![]() $p = 2$
and that
$p = 2$
and that
![]() $F_2$
is a square. If
$F_2$
is a square. If
![]() $\sqrt {F_2}$
is homogeneous, then we may assume
$\sqrt {F_2}$
is homogeneous, then we may assume
![]() $F_2 = x^2$
, we may assume
$F_2 = x^2$
, we may assume
![]() $F_3$
has
$F_3$
has
![]() $y^2 z$
or
$y^2 z$
or
![]() $z^3$
, and then we have
$z^3$
, and then we have
![]() $(a,b,c) = (1,1,0)$
, and hence
$(a,b,c) = (1,1,0)$
, and hence
![]() $F \in k[[x^2,xy,y^2,z]]$
. If
$F \in k[[x^2,xy,y^2,z]]$
. If
![]() $\sqrt {F_2}$
is not homogeneous, then we may assume
$\sqrt {F_2}$
is not homogeneous, then we may assume
![]() $F_2 = x^2 + z^2$
and
$F_2 = x^2 + z^2$
and
![]() $a = 1$
and
$a = 1$
and
![]() $c = 0$
, and then again we have
$c = 0$
, and then again we have
![]() $(a,b,c) = (1,1,0)$
, and hence
$(a,b,c) = (1,1,0)$
, and hence
![]() $F \in k[[x^2,xy,y^2,z]]$
, and
$F \in k[[x^2,xy,y^2,z]]$
, and
![]() $F_3$
has
$F_3$
has
![]() $x y z$
,
$x y z$
,
![]() $y^2 z$
,
$y^2 z$
,
![]() $z^3$
, or
$z^3$
, or
![]() $x^2 z$
.
$x^2 z$
.
Assume (
![]() $F_2$
is
$F_2$
is
![]() $x^2$
or
$x^2$
or
![]() $x^2 + z^2$
and)
$x^2 + z^2$
and)
![]() $F_3$
contains
$F_3$
contains
![]() $y^2 z$
. Furthermore, since
$y^2 z$
. Furthermore, since
![]() $F \notin (x,y)^2$
, we see that F has
$F \notin (x,y)^2$
, we see that F has
![]() $z^l$
(
$z^l$
(
![]() $l \geq 2$
). We have
$l \geq 2$
). We have
![]() $F \equiv x^2 + y^2 z + z^l \pmod {(x^4, x^3 y, x^2 y^2, x y^3, y^4, x^2 z, x y z, y^2 z^2, z^{l+1})}$
. Write
$F \equiv x^2 + y^2 z + z^l \pmod {(x^4, x^3 y, x^2 y^2, x y^3, y^4, x^2 z, x y z, y^2 z^2, z^{l+1})}$
. Write
![]() $F = F_0(x^2, y^2, z) + xy F_1(x^2, y^2, z)$
. Then there exist unique
$F = F_0(x^2, y^2, z) + xy F_1(x^2, y^2, z)$
. Then there exist unique
![]() $f, g \in k[[z]]$
such that
$f, g \in k[[z]]$
such that
![]() $F_0 \in (x^2 - f(z)^2, y^2 - g(z)^2)$
, and they satisfy
$F_0 \in (x^2 - f(z)^2, y^2 - g(z)^2)$
, and they satisfy
![]() $l = \min \{2 \operatorname {\mathrm {ord}}_z(f), 2 \operatorname {\mathrm {ord}}_z(g) + 1\}$
. If l is even, then, by replacing y with
$l = \min \{2 \operatorname {\mathrm {ord}}_z(f), 2 \operatorname {\mathrm {ord}}_z(g) + 1\}$
. If l is even, then, by replacing y with
![]() $y - x g/f$
, we may assume
$y - x g/f$
, we may assume
![]() $g = 0$
. If l is odd, then, by replacing x with
$g = 0$
. If l is odd, then, by replacing x with
![]() $x - y f/g$
, we may assume
$x - y f/g$
, we may assume
![]() $f = 0$
. We eliminate
$f = 0$
. We eliminate
![]() $a_{hij}$
with
$a_{hij}$
with
![]() $h \geq 2$
,
$h \geq 2$
,
![]() $(h,i,j) \neq (2,0,0)$
, by replacing F with
$(h,i,j) \neq (2,0,0)$
, by replacing F with
![]() $(1 + a_{hij} x^{h-2} y^i z^j) F$
, and
$(1 + a_{hij} x^{h-2} y^i z^j) F$
, and
![]() $a_{hij}$
with
$a_{hij}$
with
![]() $i \geq 2$
,
$i \geq 2$
,
![]() $(h,i,j) \neq (0,2,0), (0,2,1)$
, by replacing z with
$(h,i,j) \neq (0,2,0), (0,2,1)$
, by replacing z with
![]() $z + a_{hij} x^h y^{i-2} z^j$
. We obtain
$z + a_{hij} x^h y^{i-2} z^j$
. We obtain
![]() $F = x^2 + y^2 z + z^l u(z) + x y e(z)$
, where
$F = x^2 + y^2 z + z^l u(z) + x y e(z)$
, where
![]() $e(z) \in k[[z]]$
and
$e(z) \in k[[z]]$
and
![]() $u(z) \in k[[z]]^*$
. We have
$u(z) \in k[[z]]^*$
. We have
![]() $e(z) \neq 0$
, since if
$e(z) \neq 0$
, since if
![]() $e(z) = 0$
, then
$e(z) = 0$
, then
![]() $F = F_0 \in ((x - f(z))^2, (y - g(z))^2)$
, which is absurd. Write
$F = F_0 \in ((x - f(z))^2, (y - g(z))^2)$
, which is absurd. Write
![]() $e(z) = z^k v(z)$
,
$e(z) = z^k v(z)$
,
![]() $k \geq 1$
, and
$k \geq 1$
, and
![]() $v(z) \in k[[z]]^*$
. It is
$v(z) \in k[[z]]^*$
. It is
![]() $D_{2k+l}^{\lfloor l/2 \rfloor }$
. If l is even, then, since
$D_{2k+l}^{\lfloor l/2 \rfloor }$
. If l is even, then, since
![]() $F_0 \in (x^2 - f(z)^2, y^2 - g(z)^2)$
and
$F_0 \in (x^2 - f(z)^2, y^2 - g(z)^2)$
and
![]() $g = 0$
, we have
$g = 0$
, we have
![]() $z^l u(z) = f(z)^2$
and hence
$z^l u(z) = f(z)^2$
and hence
![]() $u(z)$
is a square, and then by replacing x with
$u(z)$
is a square, and then by replacing x with
![]() $u(z)^{1/2} x$
and by replacing F with a unit multiple, we obtain
$u(z)^{1/2} x$
and by replacing F with a unit multiple, we obtain
![]() $F = x^2 + y^2 z u'(z) + z^l + x y e(z)$
for some
$F = x^2 + y^2 z u'(z) + z^l + x y e(z)$
for some
![]() $u'(z) \in k[[z]]^*$
. Similarly, if l is odd, then, since
$u'(z) \in k[[z]]^*$
. Similarly, if l is odd, then, since
![]() $f = 0$
, we have
$f = 0$
, we have
![]() $z^l u(z) = z g(z)^2$
and hence
$z^l u(z) = z g(z)^2$
and hence
![]() $u(z)$
is a square, and then (by replacing y) we obtain
$u(z)$
is a square, and then (by replacing y) we obtain
![]() $F = x^2 u'(z) + y^2 z + z^l + x y e(z)$
. By replacing
$F = x^2 u'(z) + y^2 z + z^l + x y e(z)$
. By replacing
![]() $x,y,z,F$
with unit multiples, we can achieve
$x,y,z,F$
with unit multiples, we can achieve
![]() $u' = v = 1$
.
$u' = v = 1$
.
Assume
![]() $F_2 = x^2$
and
$F_2 = x^2$
and
![]() $F_3$
has
$F_3$
has
![]() $z^3$
but no
$z^3$
but no
![]() $y^2z$
. To define an RDP, F must have
$y^2z$
. To define an RDP, F must have
![]() $y^4$
and must have
$y^4$
and must have
![]() $xyz$
or
$xyz$
or
![]() $xy^3$
. If F has
$xy^3$
. If F has
![]() $xyz$
, then it is
$xyz$
, then it is
![]() $E_7^3$
. We have
$E_7^3$
. We have
 $$ \begin{align*} &\qquad \quad F = x^2 + y^4 + z^3 u_1+ x y z u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j \\ &\qquad \quad + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i + \sum_{(h,i) \in S_4} d_{hi} x^h y^i, \\ S_1 &= \{(3,1,0), (1,3,0), (1,5,0), (0,2,2), (2,0,1), (2,0,2), (0,4,1), (0,4,2)\}, \\ &\quad S_2 = \{(4,0), (5,1)\}, \qquad S_3 = \{(0,6), (1,7)\}, \qquad S_4 = \{(2,2)\}, \end{align*} $$
$$ \begin{align*} &\qquad \quad F = x^2 + y^4 + z^3 u_1+ x y z u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j \\ &\qquad \quad + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i + \sum_{(h,i) \in S_4} d_{hi} x^h y^i, \\ S_1 &= \{(3,1,0), (1,3,0), (1,5,0), (0,2,2), (2,0,1), (2,0,2), (0,4,1), (0,4,2)\}, \\ &\quad S_2 = \{(4,0), (5,1)\}, \qquad S_3 = \{(0,6), (1,7)\}, \qquad S_4 = \{(2,2)\}, \end{align*} $$
where
![]() $a_{hij} \in k$
,
$a_{hij} \in k$
,
![]() $b_{hi} = \sum _{j = 0}^{2} b_{hij} z^j$
with
$b_{hi} = \sum _{j = 0}^{2} b_{hij} z^j$
with
![]() $b_{hij} \in k[[x^2]]$
,
$b_{hij} \in k[[x^2]]$
,
![]() $c_{hi} = \sum _{j = 0}^{2} c_{hij} z^j$
with
$c_{hi} = \sum _{j = 0}^{2} c_{hij} z^j$
with
![]() $c_{hij} \in k[[y^2]]$
,
$c_{hij} \in k[[y^2]]$
,
![]() $d_{hi} \in k[[x^2, x y, y^2]]$
, and
$d_{hi} \in k[[x^2, x y, y^2]]$
, and
![]() $u_1,u_2 \in k[[x^2, x y, y^2, z]]^*$
. We may assume
$u_1,u_2 \in k[[x^2, x y, y^2, z]]^*$
. We may assume
![]() $u_1, u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We replace z with
$u_1, u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We replace z with
![]() $z + a_{310} x^2 + a_{130} y^2 + a_{150} y^4$
, x with
$z + a_{310} x^2 + a_{130} y^2 + a_{150} y^4$
, x with
![]() $x + t y z$
(which eliminates
$x + t y z$
(which eliminates
![]() $a_{022}$
), y with
$a_{022}$
), y with
![]() $y + a_{201} x + a_{202} x z$
, and x with
$y + a_{201} x + a_{202} x z$
, and x with
![]() $x + a_{041} y^3 + a_{042} y^3 z$
, and thus eliminate all
$x + a_{041} y^3 + a_{042} y^3 z$
, and thus eliminate all
![]() $a_{hij}$
(
$a_{hij}$
(
![]() $(h,i,j) \in S_1$
). We replace F with
$(h,i,j) \in S_1$
). We replace F with
![]() $(1 + x^2 b_{40} + y^2 c_{06}) F$
, F with
$(1 + x^2 b_{40} + y^2 c_{06}) F$
, F with
![]() $(1 + x^3 y b_{51} + x y^3 c_{17}) F$
, and z with
$(1 + x^3 y b_{51} + x y^3 c_{17}) F$
, and z with
![]() $z + d_{22} x y$
, and thus eliminate all
$z + d_{22} x y$
, and thus eliminate all
![]() $b_{hi}$
,
$b_{hi}$
,
![]() $c_{hi}$
, and
$c_{hi}$
, and
![]() $d_{hi}$
. We replace
$d_{hi}$
. We replace
![]() $x,y,z,F$
with suitable multiples and achieve
$x,y,z,F$
with suitable multiples and achieve
![]() $u_1= u_2 = 1$
.
$u_1= u_2 = 1$
.
Next, if F does not have
![]() $xyz$
but has
$xyz$
but has
![]() $x y^3$
, then it is
$x y^3$
, then it is
![]() $E_8^3$
. We have
$E_8^3$
. We have
 $$ \begin{align*} &F = x^2 + y^4 + z^3 u_1 + x y^3 u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ &\quad S_1 = \{(2,0,1), (2,0,2), (0,4,1), (0,2,2), (1,1,2), (0,6,0), (0,4,2), (0,6,1), (0,6,2), \\ &\qquad (2,2,0), (2,2,1), (2,2,2)\}, \qquad S_2 = \{(4,0), (3,1), (4,2))\}, \qquad S_3 = \{(0,8)\}, \end{align*} $$
$$ \begin{align*} &F = x^2 + y^4 + z^3 u_1 + x y^3 u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ &\quad S_1 = \{(2,0,1), (2,0,2), (0,4,1), (0,2,2), (1,1,2), (0,6,0), (0,4,2), (0,6,1), (0,6,2), \\ &\qquad (2,2,0), (2,2,1), (2,2,2)\}, \qquad S_2 = \{(4,0), (3,1), (4,2))\}, \qquad S_3 = \{(0,8)\}, \end{align*} $$
with
![]() $a_{hij}$
,
$a_{hij}$
,
![]() $b_{hi}$
,
$b_{hi}$
,
![]() $c_{hi}$
, and
$c_{hi}$
, and
![]() $u_1,u_2$
as in the previous case. We may assume
$u_1,u_2$
as in the previous case. We may assume
![]() $u_1, u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We replace F with
$u_1, u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We replace F with
![]() $(1 + a_{201} z + a_{202} z^2) F$
, x with
$(1 + a_{201} z + a_{202} z^2) F$
, x with
![]() $x + t y z$
and z with
$x + t y z$
and z with
![]() $z + t' y^2$
(which eliminates
$z + t' y^2$
(which eliminates
![]() $a_{041}$
and
$a_{041}$
and
![]() $a_{022}$
), z with
$a_{022}$
), z with
![]() $z + a_{112} x y$
, x with
$z + a_{112} x y$
, x with
![]() $x + t" y^3$
(which eliminates
$x + t" y^3$
(which eliminates
![]() $a_{060}$
), x with
$a_{060}$
), x with
![]() $x + a_{042} y z^2 + a_{061} y^3 z$
, x with
$x + a_{042} y z^2 + a_{061} y^3 z$
, x with
![]() $x + a_{062} y^3 z^2$
, and y with
$x + a_{062} y^3 z^2$
, and y with
![]() $y + (a_{220} + a_{221} z + a_{222} z^2) x$
, and thus eliminate all
$y + (a_{220} + a_{221} z + a_{222} z^2) x$
, and thus eliminate all
![]() $a_{hij}$
(
$a_{hij}$
(
![]() $(h,i,j) \in S_1$
). We replace F with
$(h,i,j) \in S_1$
). We replace F with
![]() $(1 + x^2 b_{40} + x y b_{31} + x^2 y^2 b_{42} + y^4 c_{08}) F$
, and thus eliminate all
$(1 + x^2 b_{40} + x y b_{31} + x^2 y^2 b_{42} + y^4 c_{08}) F$
, and thus eliminate all
![]() $b_{hi}$
and
$b_{hi}$
and
![]() $c_{hi}$
. We replace
$c_{hi}$
. We replace
![]() $x,y,z,F$
with suitable multiples and achieve
$x,y,z,F$
with suitable multiples and achieve
![]() $u_1 = u_2 = 1$
.
$u_1 = u_2 = 1$
.
Assume
![]() $F_2 = x^2 + z^2$
and
$F_2 = x^2 + z^2$
and
![]() $F_3$
does not have
$F_3$
does not have
![]() $y^2 z$
and has
$y^2 z$
and has
![]() $xyz$
. F moreover needs
$xyz$
. F moreover needs
![]() $x y^i$
,
$x y^i$
,
![]() $y^i z$
, or
$y^i z$
, or
![]() $y^l$
. Replacing z with
$y^l$
. Replacing z with
![]() $z + xy^{i-1}$
(resp. x with
$z + xy^{i-1}$
(resp. x with
![]() $x + y^{i-1}z$
), we may assume that there are no
$x + y^{i-1}z$
), we may assume that there are no
![]() $x y^i$
(resp.
$x y^i$
(resp.
![]() $y^i z$
) of low degree. Thus, we have
$y^i z$
) of low degree. Thus, we have
 $$ \begin{align*} &\qquad\qquad\qquad\qquad\quad F \equiv x^2 + z^2 + xyz + y^{2n-2} \\ &\pmod{(x^4, x^3 y, x^2 y^2, x y^{m} (m> n), y^{2n}, x^2 z, x y z^2, y^2 z^2, y^{m} z (m > n), z^3)}, \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad\qquad\quad F \equiv x^2 + z^2 + xyz + y^{2n-2} \\ &\pmod{(x^4, x^3 y, x^2 y^2, x y^{m} (m> n), y^{2n}, x^2 z, x y z^2, y^2 z^2, y^{m} z (m > n), z^3)}, \end{align*} $$
![]() $n \geq 3$
, and this is
$n \geq 3$
, and this is
![]() $D_{2n}^{n-1}[*]$
. We eliminate
$D_{2n}^{n-1}[*]$
. We eliminate
![]() $x^h y^i$
(
$x^h y^i$
(
![]() $h ,i \geq 1$
,
$h ,i \geq 1$
,
![]() $(h, i) \neq (1, 1)$
) by replacing z with
$(h, i) \neq (1, 1)$
) by replacing z with
![]() $z + a_{hi0} x^{h-1} y^{i-1}$
, and
$z + a_{hi0} x^{h-1} y^{i-1}$
, and
![]() $x^h z^j$
and
$x^h z^j$
and
![]() $y^i z^j$
similarly. We eliminate
$y^i z^j$
similarly. We eliminate
![]() $x^h$
,
$x^h$
,
![]() $y^i$
,
$y^i$
,
![]() $z^j$
(
$z^j$
(
![]() $h \geq 3$
,
$h \geq 3$
,
![]() $i \geq 2n-1$
,
$i \geq 2n-1$
,
![]() $j \geq 3$
) by replacing F with a unit multiple. We obtain
$j \geq 3$
) by replacing F with a unit multiple. We obtain
![]() $F = x^2 + z^2 + xyz u + y^{2n-2}$
for some
$F = x^2 + z^2 + xyz u + y^{2n-2}$
for some
![]() $u \in k[[x^2, x y, y^2, z]]^*$
, and we can achieve
$u \in k[[x^2, x y, y^2, z]]^*$
, and we can achieve
![]() $u = 1$
.
$u = 1$
.
Assume
![]() $F_2 = x^2 + z^2$
and
$F_2 = x^2 + z^2$
and
![]() $F_3$
does not have
$F_3$
does not have
![]() $y^2 z$
nor
$y^2 z$
nor
![]() $xyz$
. By replacing F with
$xyz$
. By replacing F with
![]() $(1 + a_{201} x^2 z)^{-1} F$
, we may assume that F does not have
$(1 + a_{201} x^2 z)^{-1} F$
, we may assume that F does not have
![]() $x^2 z$
. Then F has
$x^2 z$
. Then F has
![]() $z^3$
and F moreover needs
$z^3$
and F moreover needs
![]() $xy^3$
, and then it is
$xy^3$
, and then it is
![]() $E_7^2$
. We have
$E_7^2$
. We have
 $$ \begin{align*} &F = x^2 + z^2 + z^3 u_1 + x y^3 u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ & \ \ S_1 = \{(0,4,0), (0,4,1), (0,6,0), (0,2,2), (3,1,0), (2,2,0), (1,1,2), (4,0,0), (2,0,2) \}, \\ &\qquad\qquad\qquad\qquad S_2 = \{(4,0), (3,1), (2,2)\}, \qquad S_3 = \{(0,4)\}, \end{align*} $$
$$ \begin{align*} &F = x^2 + z^2 + z^3 u_1 + x y^3 u_2 + \sum_{(h,i,j) \in S_1} a_{hij} x^h y^i z^j + \sum_{(h,i) \in S_2} b_{hi} x^h y^i + \sum_{(h,i) \in S_3} c_{hi} x^h y^i, \\ & \ \ S_1 = \{(0,4,0), (0,4,1), (0,6,0), (0,2,2), (3,1,0), (2,2,0), (1,1,2), (4,0,0), (2,0,2) \}, \\ &\qquad\qquad\qquad\qquad S_2 = \{(4,0), (3,1), (2,2)\}, \qquad S_3 = \{(0,4)\}, \end{align*} $$
with
![]() $a_{hij}$
,
$a_{hij}$
,
![]() $b_{hi}$
,
$b_{hi}$
,
![]() $c_{hi}$
, and
$c_{hi}$
, and
![]() $u_1,u_2$
as in the case of
$u_1,u_2$
as in the case of
![]() $E_7^3$
, and moreover
$E_7^3$
, and moreover
![]() $b_{hi} \in (x^2, z)$
and
$b_{hi} \in (x^2, z)$
and
![]() $c_{hi} \in (y^4, y^2 z, z^2)$
. We may assume
$c_{hi} \in (y^4, y^2 z, z^2)$
. We may assume
![]() $u_1, u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We replace z with
$u_1, u_2 \equiv 1 \pmod {\mathfrak {m}}$
. We replace z with
![]() $z + a_{040}^{1/2} y^2$
, x with
$z + a_{040}^{1/2} y^2$
, x with
![]() $x + a_{041} y z$
, x with
$x + a_{041} y z$
, x with
![]() $x + t y^3$
(which eliminates
$x + t y^3$
(which eliminates
![]() $a_{060}$
), F with
$a_{060}$
), F with
![]() $(1 + a_{022} y^2) F$
, y with
$(1 + a_{022} y^2) F$
, y with
![]() $y + t' x$
and z with
$y + t' x$
and z with
![]() $z + t" x y$
and F with
$z + t" x y$
and F with
![]() $(1 + t"' x y) F$
(which eliminates
$(1 + t"' x y) F$
(which eliminates
![]() $a_{310}$
,
$a_{310}$
,
![]() $a_{220}$
, and
$a_{220}$
, and
![]() $a_{112}$
), z with
$a_{112}$
), z with
![]() $z + t"" x^2$
and F with
$z + t"" x^2$
and F with
![]() $(1 + t""' x^2) F$
(which eliminates
$(1 + t""' x^2) F$
(which eliminates
![]() $a_{400}$
and
$a_{400}$
and
![]() $a_{202}$
), and thus eliminate all
$a_{202}$
), and thus eliminate all
![]() $a_{hij}$
(
$a_{hij}$
(
![]() $(h,i,j) \in S_1$
). We replace x with
$(h,i,j) \in S_1$
). We replace x with
![]() $x + y c_{04}$
and F with
$x + y c_{04}$
and F with
![]() $(1 + b_{40} x^2 + b_{31} x y + b_{22} y^2) F$
to eliminate all
$(1 + b_{40} x^2 + b_{31} x y + b_{22} y^2) F$
to eliminate all
![]() $b_{hi}$
and
$b_{hi}$
and
![]() $c_{hi}$
. We replace
$c_{hi}$
. We replace
![]() $x,y,z,F$
with suitable multiples and achieve
$x,y,z,F$
with suitable multiples and achieve
![]() $u_1 = u_2 = 1$
.
$u_1 = u_2 = 1$
.
4.3
 $\mu _n$
-actions on RDPs
$\mu _n$
-actions on RDPs
In this section, we classify
![]() $\mu _n$
-actions on RDPs under each of the following assumptions.
$\mu _n$
-actions on RDPs under each of the following assumptions.
-
• w is not fixed by
 $\mu _n$
(Proposition 4.12).
$\mu _n$
(Proposition 4.12). -
•
 $n = p^e$
, and the subgroup scheme
$n = p^e$
, and the subgroup scheme
 $\mu _p$
fixes w and is symplectic (Proposition 4.13).
$\mu _p$
fixes w and is symplectic (Proposition 4.13). -
• w is fixed by
 $\mu _n$
and the action is symplectic (Proposition 4.14).
$\mu _n$
and the action is symplectic (Proposition 4.14).
In Propositions 4.13 and 4.14, we use the convention that a smooth point is of type
![]() $A_0$
.
$A_0$
.
Lemma 4.11. Let X be a k-scheme equipped with a
![]() $\mu _{p^2}$
-action. Let
$\mu _{p^2}$
-action. Let
![]() $\pi _1 \colon X \to X_1 = X / \mu _p$
be the quotient morphism by the action of the subgroup scheme
$\pi _1 \colon X \to X_1 = X / \mu _p$
be the quotient morphism by the action of the subgroup scheme
![]() $\mu _p \subset \mu _{p^2}$
. If
$\mu _p \subset \mu _{p^2}$
. If
![]() $w \in X$
is non-fixed by the action of
$w \in X$
is non-fixed by the action of
![]() $\mu _p$
, then
$\mu _p$
, then
![]() $\pi _1(w) \in X_1$
is non-fixed by the action of
$\pi _1(w) \in X_1$
is non-fixed by the action of
![]() $\mu _{p^2}/\mu _p$
.
$\mu _{p^2}/\mu _p$
.
Proof. Let
![]() $\mathcal {O}_{X,w} = B = \bigoplus _{i \in \mathbb Z/p^2\mathbb Z} B_i$
be the corresponding decomposition. Since w is non-fixed by
$\mathcal {O}_{X,w} = B = \bigoplus _{i \in \mathbb Z/p^2\mathbb Z} B_i$
be the corresponding decomposition. Since w is non-fixed by
![]() $\mu _p$
, there exists
$\mu _p$
, there exists
![]() $y \in \mathfrak {m}_{w} \subset B$
with
$y \in \mathfrak {m}_{w} \subset B$
with
![]() $1 + y \in \bigoplus _{i \equiv 1 \pmod {p}} B_i$
(Lemma 2.9). Then, since
$1 + y \in \bigoplus _{i \equiv 1 \pmod {p}} B_i$
(Lemma 2.9). Then, since
![]() $y^p \in \mathfrak {m}_{\pi _1(w)} \subset \mathcal {O}_{X_1, \pi _1(w)}$
satisfies
$y^p \in \mathfrak {m}_{\pi _1(w)} \subset \mathcal {O}_{X_1, \pi _1(w)}$
satisfies
![]() $1 + y^p = (1 + y)^p \in B_p$
, we conclude by Proposition 2.8 that
$1 + y^p = (1 + y)^p \in B_p$
, we conclude by Proposition 2.8 that
![]() $\pi _1(w)$
is non-fixed by
$\pi _1(w)$
is non-fixed by
![]() $\mu _{p^2}/\mu _p$
.
$\mu _{p^2}/\mu _p$
.
Suppose X is a scheme equipped with a
![]() $\mu _n$
-action,
$\mu _n$
-action,
![]() $n = p^e r$
with
$n = p^e r$
with
![]() $p \nmid r$
, and
$p \nmid r$
, and
![]() $w \in X$
is a closed point fixed by
$w \in X$
is a closed point fixed by
![]() $\mu _r \subset \mu _n$
. Let f be the maximal integer with
$\mu _r \subset \mu _n$
. Let f be the maximal integer with
![]() $0 \leq f \leq e$
such that the subgroup scheme
$0 \leq f \leq e$
such that the subgroup scheme
![]() $\mu _{p^f} \subset \mu _{p^e} \subset \mu _n$
fixes w. We say that
$\mu _{p^f} \subset \mu _{p^e} \subset \mu _n$
fixes w. We say that
![]() $\mu _{p^f r}$
is the stabilizer of w and denote it by
$\mu _{p^f r}$
is the stabilizer of w and denote it by
![]() $\operatorname {\mathrm {Stab}}(w)$
.
$\operatorname {\mathrm {Stab}}(w)$
.
Proposition 4.12. Let
![]() $\mathcal {O}_{X,w}$
, together with a
$\mathcal {O}_{X,w}$
, together with a
![]() $\mu _n$
-action, be as in the beginning of §4, and assume w is an RDP. Write
$\mu _n$
-action, be as in the beginning of §4, and assume w is an RDP. Write
![]() $n = p^e r$
with
$n = p^e r$
with
![]() $p \nmid r$
, and
$p \nmid r$
, and
![]() $\operatorname {\mathrm {Stab}}(w) = \mu _{p^f r}$
. Suppose
$\operatorname {\mathrm {Stab}}(w) = \mu _{p^f r}$
. Suppose
![]() $\operatorname {\mathrm {Stab}}(w) \subsetneq \mu _n$
(hence
$\operatorname {\mathrm {Stab}}(w) \subsetneq \mu _n$
(hence
![]() $f < e$
, in particular
$f < e$
, in particular
![]() $e \geq 1$
). Then there exist
$e \geq 1$
). Then there exist
![]() $x,y,z \in \mathfrak {m}$
generating
$x,y,z \in \mathfrak {m}$
generating
![]() $\mathfrak {m}$
, with
$\mathfrak {m}$
, with
![]() $x,y,1+z$
homogeneous such that, up to replacing r with a multiple and up to
$x,y,1+z$
homogeneous such that, up to replacing r with a multiple and up to
![]() $\operatorname {\mathrm {Aut}}(\mu _n) = (\mathbb Z/n\mathbb Z)^*$
, the weights and the type of singularity are as in Table 5.
$\operatorname {\mathrm {Aut}}(\mu _n) = (\mathbb Z/n\mathbb Z)^*$
, the weights and the type of singularity are as in Table 5.
Table 5 Non-fixed
![]() $\mu _n$
-actions on RDPs (listed in order of appearance in the proof).
$\mu _n$
-actions on RDPs (listed in order of appearance in the proof).

(*): In the cases where
![]() $n = 4(m-1)$
or
$n = 4(m-1)$
or
![]() $n = 4m$
,
$n = 4m$
,
![]() $p^e$
is the highest power of
$p^e$
is the highest power of
![]() $p = 2$
dividing n.
$p = 2$
dividing n.
In this case, we do not pursue the exact equation, and the equations in Table 5 are merely examples.
Proof. We first show that there exist elements
![]() $x,y,z \in \mathfrak {m}$
generating
$x,y,z \in \mathfrak {m}$
generating
![]() $\mathfrak {m}$
and satisfying
$\mathfrak {m}$
and satisfying
![]() $\operatorname {\mathrm {wt}}(x,y,1+z) = (a,b,c)$
with
$\operatorname {\mathrm {wt}}(x,y,1+z) = (a,b,c)$
with
![]() $c = n/p^{e-f} = p^f r$
. Since the stabilizer of the
$c = n/p^{e-f} = p^f r$
. Since the stabilizer of the
![]() $\mu _{n}$
-action is
$\mu _{n}$
-action is
![]() $\mu _{p^f r} \subsetneq \mu _{n }$
, there exist
$\mu _{p^f r} \subsetneq \mu _{n }$
, there exist
![]() $i \in \mathbb Z/n\mathbb Z$
and a homogeneous element t of weight i such that
$i \in \mathbb Z/n\mathbb Z$
and a homogeneous element t of weight i such that
![]() $t \notin \mathfrak {m}$
and
$t \notin \mathfrak {m}$
and
![]() $\gcd \{i, n\} = p^f r$
. We may assume
$\gcd \{i, n\} = p^f r$
. We may assume
![]() $t \equiv 1 \pmod {\mathfrak {m}}$
, and then
$t \equiv 1 \pmod {\mathfrak {m}}$
, and then
![]() $z' := -1 + t \in \mathfrak {m}$
satisfies
$z' := -1 + t \in \mathfrak {m}$
satisfies
![]() $\operatorname {\mathrm {wt}}(1 + z') = i$
. Take an integer q such that
$\operatorname {\mathrm {wt}}(1 + z') = i$
. Take an integer q such that
![]() $q i = p^f r$
(in
$q i = p^f r$
(in
![]() $\mathbb Z/n\mathbb Z$
), and then
$\mathbb Z/n\mathbb Z$
), and then
![]() $1 + z := (1 + z')^q$
satisfies
$1 + z := (1 + z')^q$
satisfies
![]() $z \in \mathfrak {m}$
and
$z \in \mathfrak {m}$
and
![]() $\operatorname {\mathrm {wt}}(1 + z) = p^f r$
. Now, take
$\operatorname {\mathrm {wt}}(1 + z) = p^f r$
. Now, take
![]() $x^{\prime (1)}, x^{\prime (2)}, x^{\prime (3)}$
generating
$x^{\prime (1)}, x^{\prime (2)}, x^{\prime (3)}$
generating
![]() $\mathfrak {m}$
. We may assume each
$\mathfrak {m}$
. We may assume each
![]() $x^{\prime (h)}$
is homogeneous with respect to
$x^{\prime (h)}$
is homogeneous with respect to
![]() $\mu _{p^f r}$
, that is, there exists
$\mu _{p^f r}$
, that is, there exists
![]() $i^{(1)}, i^{(2)}, i^{(3)} \in \mathbb Z/n\mathbb Z$
such that
$i^{(1)}, i^{(2)}, i^{(3)} \in \mathbb Z/n\mathbb Z$
such that
![]() $x^{\prime (h)} = \sum _{j = 0}^{p^{e-f}-1} x^{\prime (h,j)}$
with
$x^{\prime (h)} = \sum _{j = 0}^{p^{e-f}-1} x^{\prime (h,j)}$
with
![]() $\operatorname {\mathrm {wt}}(x^{\prime (h,j)}) = i^{(h)} + j p^f r$
. Let
$\operatorname {\mathrm {wt}}(x^{\prime (h,j)}) = i^{(h)} + j p^f r$
. Let
![]() $x^{(h)} := \sum _{j = 0}^{p^{e-f}-1} (1+z)^{-j} x^{\prime (h,j)}$
. Then
$x^{(h)} := \sum _{j = 0}^{p^{e-f}-1} (1+z)^{-j} x^{\prime (h,j)}$
. Then
![]() $\operatorname {\mathrm {wt}}(x^{(h)}) = i^{(h)}$
and, since
$\operatorname {\mathrm {wt}}(x^{(h)}) = i^{(h)}$
and, since
![]() $x^{(h)} \equiv x^{\prime (h)} \pmod {(z)}$
, the elements
$x^{(h)} \equiv x^{\prime (h)} \pmod {(z)}$
, the elements
![]() $x^{(1)}, x^{(2)}, x^{(3)}, z$
generate
$x^{(1)}, x^{(2)}, x^{(3)}, z$
generate
![]() $\mathfrak {m}$
. We can omit one of these four elements, which cannot be z since
$\mathfrak {m}$
. We can omit one of these four elements, which cannot be z since
![]() $\mathfrak {m}$
is not generated by homogeneous elements.
$\mathfrak {m}$
is not generated by homogeneous elements.
In this proof, by a monomial, we mean a polynomial of the form
![]() $x^i y^j z^{p^{e-f} l} (1+z)^m$
with
$x^i y^j z^{p^{e-f} l} (1+z)^m$
with
![]() $0 \leq m < p^{e-f}$
. Any polynomial (resp. formal power series) is uniquely expressed as a finite (resp. possibly infinite) sum of monomials with k-coefficients, and we say that a polynomial or a formal power series has a monomial if its coefficient is nonzero. Expressions such as
$0 \leq m < p^{e-f}$
. Any polynomial (resp. formal power series) is uniquely expressed as a finite (resp. possibly infinite) sum of monomials with k-coefficients, and we say that a polynomial or a formal power series has a monomial if its coefficient is nonzero. Expressions such as
![]() $F = x^2 + y^3 (1+z) + \cdots $
will indicate that F has these monomials. However, when we say of degree m part
$F = x^2 + y^3 (1+z) + \cdots $
will indicate that F has these monomials. However, when we say of degree m part
![]() $F_m$
of F, this is understood with respect to the usual monomials
$F_m$
of F, this is understood with respect to the usual monomials
![]() $x^i y^j z^l$
.
$x^i y^j z^l$
.
Assume the degree
![]() $2$
part
$2$
part
![]() $F_2$
of F is either irreducible or the product of two distinct homogeneous linear factors. Then we may assume
$F_2$
of F is either irreducible or the product of two distinct homogeneous linear factors. Then we may assume
![]() $F = xy (1+z)^i + \cdots $
, and F must have
$F = xy (1+z)^i + \cdots $
, and F must have
![]() $z^{m'} (1+z)^j$
, we may assume
$z^{m'} (1+z)^j$
, we may assume
![]() $i = j = 0$
by replacing y and F, and it is
$i = j = 0$
by replacing y and F, and it is
![]() $A_{m'-1}$
with
$A_{m'-1}$
with
![]() $m' = p^{e-f} m$
.
$m' = p^{e-f} m$
.
Assume
![]() $F_2$
is the product of two distinct nonhomogeneous linear factors. Then we have
$F_2$
is the product of two distinct nonhomogeneous linear factors. Then we have
![]() $p \neq 2$
and we may assume
$p \neq 2$
and we may assume
![]() $F = x^2 (1+z)^i + y^2 (1+z)^j + z^{m'} (1+z)^k + \cdots $
and
$F = x^2 (1+z)^i + y^2 (1+z)^j + z^{m'} (1+z)^k + \cdots $
and
![]() $b \equiv a + r/2 \pmod {r}$
. We may assume
$b \equiv a + r/2 \pmod {r}$
. We may assume
![]() $k = 0$
by replacing F with
$k = 0$
by replacing F with
![]() $(1+z)^{-k} F$
and
$(1+z)^{-k} F$
and
![]() $i = j = 0$
by replacing x and y with
$i = j = 0$
by replacing x and y with
![]() $x (1+z)^{i(p^e+1)/2}$
and
$x (1+z)^{i(p^e+1)/2}$
and
![]() $y (1+z)^{j(p^e+1)/2}$
. We have
$y (1+z)^{j(p^e+1)/2}$
. We have
![]() $2a = 2b = 0$
and then we have
$2a = 2b = 0$
and then we have
![]() $f = 0$
and
$f = 0$
and
![]() $r = 2$
. (Otherwise,
$r = 2$
. (Otherwise,
![]() $a,b,c$
cannot generate
$a,b,c$
cannot generate
![]() $\mathbb Z/p^e r \mathbb Z$
.) It is
$\mathbb Z/p^e r \mathbb Z$
.) It is
![]() $A_{m'-1}$
with
$A_{m'-1}$
with
![]() $m' = p^e m$
, and we may assume
$m' = p^e m$
, and we may assume
![]() $(a,b) = (0,n/2)$
.
$(a,b) = (0,n/2)$
.
Assume
![]() $p \geq 5$
and
$p \geq 5$
and
![]() $F_2$
is a square. We may assume
$F_2$
is a square. We may assume
![]() $F_2 = x^2$
,
$F_2 = x^2$
,
![]() $F_3 = y^3$
,
$F_3 = y^3$
,
![]() $F = x^2 + y^3 + \cdots $
, and then F must have
$F = x^2 + y^3 + \cdots $
, and then F must have
![]() $z^5 (1+z)^i$
and we have
$z^5 (1+z)^i$
and we have
![]() $p = 5$
, it is
$p = 5$
, it is
![]() $E_8^0$
, and we may assume
$E_8^0$
, and we may assume
![]() $i = 0$
. By
$i = 0$
. By
![]() $2a = 3b = 0$
, we have
$2a = 3b = 0$
, we have
![]() $n \mid 30$
and we may assume
$n \mid 30$
and we may assume
![]() $a = 15$
and
$a = 15$
and
![]() $b = 10$
.
$b = 10$
.
Assume
![]() $p = 3$
and
$p = 3$
and
![]() $F_2$
is a square. We may assume
$F_2$
is a square. We may assume
![]() $F = x^2 + \cdots $
. We may assume
$F = x^2 + \cdots $
. We may assume
![]() $F_3 \bmod (x)$
is either
$F_3 \bmod (x)$
is either
![]() $y^3$
,
$y^3$
,
![]() $z^3$
, or
$z^3$
, or
![]() $y^3 + z^3$
. If
$y^3 + z^3$
. If
![]() $F = x^2 + y^3 + \cdots $
, then F must have
$F = x^2 + y^3 + \cdots $
, then F must have
![]() $y z^3$
and it is
$y z^3$
and it is
![]() $E_7^0$
. If
$E_7^0$
. If
![]() $F = x^2 + z^3 + \cdots $
, then F must have
$F = x^2 + z^3 + \cdots $
, then F must have
![]() $y^4$
or
$y^4$
or
![]() $y^5$
and it is
$y^5$
and it is
![]() $E_6^0$
or
$E_6^0$
or
![]() $E_8^0$
. If
$E_8^0$
. If
![]() $F = x^2 + y^3 + z^3 (1+z)^i + \cdots $
, then we may assume
$F = x^2 + y^3 + z^3 (1+z)^i + \cdots $
, then we may assume
![]() $i = 1$
(if
$i = 1$
(if
![]() $i = 0$
, then by replacing z with
$i = 0$
, then by replacing z with
![]() $y (1 + z)^l + z $
, we reduce this case to the previous case) and then it is
$y (1 + z)^l + z $
, we reduce this case to the previous case) and then it is
![]() $E_6^0$
.
$E_6^0$
.
Assume
![]() $p = 2$
and
$p = 2$
and
![]() $F_2$
is a square. We may assume
$F_2$
is a square. We may assume
![]() $F_2$
is
$F_2$
is
![]() $x^2$
,
$x^2$
,
![]() $z^2$
,
$z^2$
,
![]() $x^2 + z^2$
,
$x^2 + z^2$
,
![]() $x^2 + y^2$
, or
$x^2 + y^2$
, or
![]() $x^2 + y^2 + z^2$
.
$x^2 + y^2 + z^2$
.
Assume
![]() $F_2 = x^2$
. We may assume
$F_2 = x^2$
. We may assume
![]() $F = x^2 + \cdots $
. Then F must have
$F = x^2 + \cdots $
. Then F must have
![]() $y z^2 (1+z)^i$
or
$y z^2 (1+z)^i$
or
![]() $y^3 (1+z)^j$
. If F has
$y^3 (1+z)^j$
. If F has
![]() $y z^2 (1+z)^i$
, then we may assume
$y z^2 (1+z)^i$
, then we may assume
![]() $i = 0$
and F must have
$i = 0$
and F must have
![]() $x y^m (1+z)^i$
(
$x y^m (1+z)^i$
(
![]() $m \geq 2$
) or
$m \geq 2$
) or
![]() $y^m (1+z)$
(
$y^m (1+z)$
(
![]() $m \geq 3$
). In the former case, we may assume
$m \geq 3$
). In the former case, we may assume
![]() $i = 0$
(by replacing x with
$i = 0$
(by replacing x with
![]() $x (1+z)^i$
) and we have
$x (1+z)^i$
) and we have
![]() $D_{2m+1}^0$
with
$D_{2m+1}^0$
with
![]() $(a,b,c) = (2m,2,2m-1)$
,
$(a,b,c) = (2m,2,2m-1)$
,
![]() $n \mid 2(2m-1)$
. In the latter case, we have
$n \mid 2(2m-1)$
. In the latter case, we have
![]() $D_{2m}^0$
with
$D_{2m}^0$
with
![]() $(a,b,c) = (1,2,2(m-1))$
,
$(a,b,c) = (1,2,2(m-1))$
,
![]() $n \mid 4(m-1)$
. Now, assume that F does not have
$n \mid 4(m-1)$
. Now, assume that F does not have
![]() $y z^2 (1+z)^i$
and has
$y z^2 (1+z)^i$
and has
![]() $y^3 (1+z)^j$
. We may assume
$y^3 (1+z)^j$
. We may assume
![]() $j = 0$
. Then F must have either
$j = 0$
. Then F must have either
![]() $x z^2 (1+z)^i$
or
$x z^2 (1+z)^i$
or
![]() $z^4 (1+z)^i$
. If F has
$z^4 (1+z)^i$
. If F has
![]() $x z^2 (1+z)^i$
, then we may assume
$x z^2 (1+z)^i$
, then we may assume
![]() $i = 0$
and then
$i = 0$
and then
![]() $F = x^2 + y^3 + x z^2 + \cdots $
is
$F = x^2 + y^3 + x z^2 + \cdots $
is
![]() $E_6^0$
, and we have
$E_6^0$
, and we have
![]() $e = 1$
,
$e = 1$
,
![]() $f = 0$
,
$f = 0$
,
![]() $a = 0$
, and
$a = 0$
, and
![]() $c = n/2$
. If F does not have
$c = n/2$
. If F does not have
![]() $x z^2 (1+z)^i$
and has
$x z^2 (1+z)^i$
and has
![]() $z^4 (1+z)^i$
, then we may assume
$z^4 (1+z)^i$
, then we may assume
![]() $i = 1$
and then
$i = 1$
and then
![]() $F = x^2 + y^3 + z^4 (1+z) + \cdots $
is
$F = x^2 + y^3 + z^4 (1+z) + \cdots $
is
![]() $E_8^0$
, and we have
$E_8^0$
, and we have
![]() $e - f \leq 2$
,
$e - f \leq 2$
,
![]() $f = 1$
,
$f = 1$
,
![]() $(a,b,c) \equiv (1,2/3,2) \pmod {2^e}$
.
$(a,b,c) \equiv (1,2/3,2) \pmod {2^e}$
.
Assume
![]() $F_2 = z^2$
. We have
$F_2 = z^2$
. We have
![]() $e - f = 1$
. Suppose F has
$e - f = 1$
. Suppose F has
![]() $x^2 y (1 + z)^i$
. We may assume
$x^2 y (1 + z)^i$
. We may assume
![]() $i = 0$
. We may assume F does not have monomials
$i = 0$
. We may assume F does not have monomials
![]() $z^2 M$
(
$z^2 M$
(
![]() $M \neq 1$
) nor
$M \neq 1$
) nor
![]() $x^2 M$
(
$x^2 M$
(
![]() $M \neq 1, y$
) of low degree (by replacing F or y with
$M \neq 1, y$
) of low degree (by replacing F or y with
![]() $(1 + M)^{-1} F$
or
$(1 + M)^{-1} F$
or
![]() $y + M$
, respectively). F must have
$y + M$
, respectively). F must have
![]() $x y^m$
or
$x y^m$
or
![]() $y^m (1+z)$
and then it is
$y^m (1+z)$
and then it is
![]() $D_{2m}^0$
or
$D_{2m}^0$
or
![]() $D_{2m+1}^0$
. Now, suppose F does not have
$D_{2m+1}^0$
. Now, suppose F does not have
![]() $x^2 y (1 + z)^i$
nor
$x^2 y (1 + z)^i$
nor
![]() $x y^2 (1 + z)^i$
and has
$x y^2 (1 + z)^i$
and has
![]() $x^3 (1 + z)^i$
. We may assume
$x^3 (1 + z)^i$
. We may assume
![]() $i = 0$
. Then F must have
$i = 0$
. Then F must have
![]() $y^3 (1 + z)^j$
(
$y^3 (1 + z)^j$
(
![]() $D_4^0$
),
$D_4^0$
),
![]() $x y^3 (1 + z)^j$
(
$x y^3 (1 + z)^j$
(
![]() $E_7^0$
), or
$E_7^0$
), or
![]() $y^5 (1 + z)^j$
(
$y^5 (1 + z)^j$
(
![]() $E_8^0$
).
$E_8^0$
).
Assume
![]() $F_2 = x^2 + z^2$
. We may assume
$F_2 = x^2 + z^2$
. We may assume
![]() $F = x^2 + z^2 (1+z)^i + \cdots $
. If
$F = x^2 + z^2 (1+z)^i + \cdots $
. If
![]() $i = 0$
, then by replacing z with
$i = 0$
, then by replacing z with
![]() $z + x$
or
$z + x$
or
![]() $z + x (1+z)$
, we reduce this case to the previous case. Assume
$z + x (1+z)$
, we reduce this case to the previous case. Assume
![]() $i = 1$
. F cannot have
$i = 1$
. F cannot have
![]() $x^3 (1+z)^i$
nor
$x^3 (1+z)^i$
nor
![]() $x z^2 (1+z)^i$
. (If F has
$x z^2 (1+z)^i$
. (If F has
![]() $x^3 (1+z)^i$
, then we have
$x^3 (1+z)^i$
, then we have
![]() $2a = c = 3a + ic$
and this implies
$2a = c = 3a + ic$
and this implies
![]() $(2i+1)c = 0$
, contradicting
$(2i+1)c = 0$
, contradicting
![]() $c = n/p^{e-f}$
. Other cases are similar.) We may assume that F does not have
$c = n/p^{e-f}$
. Other cases are similar.) We may assume that F does not have
![]() $y z^2 (1+z)^i$
. If F has
$y z^2 (1+z)^i$
. If F has
![]() $y^3 (1+z)^i$
, then F does not have
$y^3 (1+z)^i$
, then F does not have
![]() $x y^2 (1+z)^j$
and it is
$x y^2 (1+z)^j$
and it is
![]() $D_4^0$
. If F does not have
$D_4^0$
. If F does not have
![]() $y^3 (1+z)^i$
and has
$y^3 (1+z)^i$
and has
![]() $x^2 y (1+z)^i$
, then F cannot have
$x^2 y (1+z)^i$
, then F cannot have
![]() $x y^2 (1+z)^j$
, and F must have
$x y^2 (1+z)^j$
, and F must have
![]() $y^{2m+1} (1+z)^j$
, and it is
$y^{2m+1} (1+z)^j$
, and it is
![]() $D_{4m}^0$
. If F does not have
$D_{4m}^0$
. If F does not have
![]() $y^3 (1+z)^i$
nor
$y^3 (1+z)^i$
nor
![]() $x^2 y (1+z)^i$
and has
$x^2 y (1+z)^i$
and has
![]() $xy^2 (1+z)^i$
, then it is
$xy^2 (1+z)^i$
, then it is
![]() $D_5^0$
. If F does not have
$D_5^0$
. If F does not have
![]() $y^3 (1+z)^i$
nor
$y^3 (1+z)^i$
nor
![]() $xy^2 (1+z)^i$
nor
$xy^2 (1+z)^i$
nor
![]() $x^2 y (1+z)^i$
, then F must have
$x^2 y (1+z)^i$
, then F must have
![]() $xy^3 (1+z)^i$
or
$xy^3 (1+z)^i$
or
![]() $y^5 (1+z)^i$
, and (we may assume
$y^5 (1+z)^i$
, and (we may assume
![]() $i = 0$
and) it is
$i = 0$
and) it is
![]() $E_7^2$
or
$E_7^2$
or
![]() $E_8^0$
. (This
$E_8^0$
. (This
![]() $E_7^2$
is the only example of
$E_7^2$
is the only example of
![]() $D_n^r$
or
$D_n^r$
or
![]() $E_n^r$
with
$E_n^r$
with
![]() $r> 0$
in this proposition.)
$r> 0$
in this proposition.)
Assume
![]() $F_2 = x^2 + y^2$
. Write
$F_2 = x^2 + y^2$
. Write
![]() $F = x^2 + y^2 (1+z)^j + \cdots $
. If
$F = x^2 + y^2 (1+z)^j + \cdots $
. If
![]() $j = 0$
, then by replacing x with
$j = 0$
, then by replacing x with
![]() $x + y (1+z)^k$
, we reduce to the
$x + y (1+z)^k$
, we reduce to the
![]() $F_2 = x^2$
case. Suppose
$F_2 = x^2$
case. Suppose
![]() $j = 1$
. We may assume F does not have monomials
$j = 1$
. We may assume F does not have monomials
![]() $x^2 M$
(
$x^2 M$
(
![]() $M \neq (1+z)^i$
) nor
$M \neq (1+z)^i$
) nor
![]() $y^2 M$
(
$y^2 M$
(
![]() $M \neq (1+z)^i$
) of low degree (by replacing F or z with
$M \neq (1+z)^i$
) of low degree (by replacing F or z with
![]() $(1 + M)^{-1} F$
or
$(1 + M)^{-1} F$
or
![]() $z + M$
, respectively). F must have
$z + M$
, respectively). F must have
![]() $x z^{2m} (1+z)^k$
or
$x z^{2m} (1+z)^k$
or
![]() $y z^{2m} (1+z)^k$
, by symmetry, we may assume F has
$y z^{2m} (1+z)^k$
, by symmetry, we may assume F has
![]() $x z^{2m} (1+z)^k$
, we may assume
$x z^{2m} (1+z)^k$
, we may assume
![]() $k = 0$
, and then it is
$k = 0$
, and then it is
![]() $D_{4m}^0$
.
$D_{4m}^0$
.
Assume
![]() $F_2 = x^2 + y^2 + z^2$
. Write
$F_2 = x^2 + y^2 + z^2$
. Write
![]() $F = x^2 (1+z)^i + y^2 (1+z)^j + z^2 (1+z)^k + \cdots $
,
$F = x^2 (1+z)^i + y^2 (1+z)^j + z^2 (1+z)^k + \cdots $
,
![]() $i,j,k \in \{0,1\}$
. If
$i,j,k \in \{0,1\}$
. If
![]() $i = j$
, then we reduce this case to
$i = j$
, then we reduce this case to
![]() $F = x^2 + z^2$
case by replacing x with
$F = x^2 + z^2$
case by replacing x with
![]() $x + y (1+z)^l$
. If
$x + y (1+z)^l$
. If
![]() $i \neq j$
, then either
$i \neq j$
, then either
![]() $i = k$
or
$i = k$
or
![]() $j = k$
and then we reduce this case to
$j = k$
and then we reduce this case to
![]() $F = x^2 + z^2$
case by replacing z with
$F = x^2 + z^2$
case by replacing z with
![]() $z + x (1+z)^l$
or
$z + x (1+z)^l$
or
![]() $z + y (1+z)^l$
.
$z + y (1+z)^l$
.
Proposition 4.13. Let
![]() $\mathcal {O}_{X,w}$
, together with a
$\mathcal {O}_{X,w}$
, together with a
![]() $\mu _n$
-action, be as in the beginning of §4. Suppose
$\mu _n$
-action, be as in the beginning of §4. Suppose
![]() $n = p^e$
with
$n = p^e$
with
![]() $p> 0$
and
$p> 0$
and
![]() $e \geq 2$
. Let
$e \geq 2$
. Let
![]() $\operatorname {\mathrm {Stab}}(w) = \mu _{p^f}$
(
$\operatorname {\mathrm {Stab}}(w) = \mu _{p^f}$
(
![]() $0 \leq f \leq e$
). Suppose
$0 \leq f \leq e$
). Suppose
![]() $f> 0$
and that the subgroup scheme
$f> 0$
and that the subgroup scheme
![]() $\mu _p \subset \operatorname {\mathrm {Stab}}(w)$
acts symplectically. Then one of the following is true.
$\mu _p \subset \operatorname {\mathrm {Stab}}(w)$
acts symplectically. Then one of the following is true.
-
• w is
 $A_{p^{e-f} m-1}$
for some integer
$A_{p^{e-f} m-1}$
for some integer
 $m \geq 1$
.
$m \geq 1$
. -
• w is
 $E_7^2$
and
$E_7^2$
and
 $(p^f, p^e) = (2, 4)$
.
$(p^f, p^e) = (2, 4)$
. -
• w is
 $D_{2n+1}^{n-1}$
(
$D_{2n+1}^{n-1}$
(
 $n \geq 2$
) or
$n \geq 2$
) or
 $E_8^3$
, and
$E_8^3$
, and
 $(p^f, p^e) = (4, 4)$
.
$(p^f, p^e) = (4, 4)$
.
Proof. Let
![]() $\mathcal {O}_{x,w} = B = \bigoplus _{i \in \mathbb Z/p^2\mathbb Z} B_i$
be the corresponding decomposition.
$\mathcal {O}_{x,w} = B = \bigoplus _{i \in \mathbb Z/p^2\mathbb Z} B_i$
be the corresponding decomposition.
Assume w is a smooth point. Since
![]() $\mu _p$
acts symplectically, the maximal ideal
$\mu _p$
acts symplectically, the maximal ideal
![]() $\mathfrak {m}$
is generated by two elements
$\mathfrak {m}$
is generated by two elements
![]() $x \in \bigoplus _{i \equiv a \pmod {p}} B_i$
and
$x \in \bigoplus _{i \equiv a \pmod {p}} B_i$
and
![]() $y \in \bigoplus _{i \equiv b \pmod {p}} B_i$
for some
$y \in \bigoplus _{i \equiv b \pmod {p}} B_i$
for some
![]() $a,b \in \mathbb Z/p^e\mathbb Z$
with
$a,b \in \mathbb Z/p^e\mathbb Z$
with
![]() $a,b \not \equiv 0$
and
$a,b \not \equiv 0$
and
![]() $a + b \equiv 0 \pmod {p}$
. Since
$a + b \equiv 0 \pmod {p}$
. Since
![]() $a,b \not \equiv 0 \pmod {p}$
, we may assume moreover
$a,b \not \equiv 0 \pmod {p}$
, we may assume moreover
![]() $x \in B_a$
and
$x \in B_a$
and
![]() $y \in B_b$
. Then w is fixed by the whole group scheme
$y \in B_b$
. Then w is fixed by the whole group scheme
![]() $\mu _{p^e}$
and hence
$\mu _{p^e}$
and hence
![]() $e = f$
. This case is done (with
$e = f$
. This case is done (with
![]() $m = 1$
: recall the convention that a smooth point is of type
$m = 1$
: recall the convention that a smooth point is of type
![]() $A_0$
).
$A_0$
).
Hereafter, we assume w is an RDP. Let
![]() $\varepsilon = 0$
if
$\varepsilon = 0$
if
![]() $e = f$
and
$e = f$
and
![]() $\varepsilon = 1$
if
$\varepsilon = 1$
if
![]() $e> f$
. By arguing as in the beginning of the proof of Proposition 4.12 and by using Proposition 4.9,
$e> f$
. By arguing as in the beginning of the proof of Proposition 4.12 and by using Proposition 4.9,
![]() $\mathfrak {m}$
is generated by three elements
$\mathfrak {m}$
is generated by three elements
![]() $x,y,z$
with
$x,y,z$
with
![]() $x \in B_a$
,
$x \in B_a$
,
![]() $y \in B_b$
, and
$y \in B_b$
, and
![]() $\varepsilon + z \in B_c$
, and we may assume
$\varepsilon + z \in B_c$
, and we may assume
![]() $a \equiv -b \not \equiv 0 \pmod {p}$
, and if
$a \equiv -b \not \equiv 0 \pmod {p}$
, and if
![]() $e> f$
then we may moreover assume
$e> f$
then we may moreover assume
![]() $c = p^f$
.
$c = p^f$
.
If
![]() $e> f$
, then, since
$e> f$
, then, since
![]() $\mu _p$
acts symplectically, it follows (from the classification given in Proposition 4.12) that either the RDP is
$\mu _p$
acts symplectically, it follows (from the classification given in Proposition 4.12) that either the RDP is
![]() $A_{m'-1}$
and then we may assume
$A_{m'-1}$
and then we may assume
![]() $F = xy + z^{m'} + \cdots $
and hence
$F = xy + z^{m'} + \cdots $
and hence
![]() $p^{e-f} \mid m'$
, or the RDP is
$p^{e-f} \mid m'$
, or the RDP is
![]() $E_7^2$
and
$E_7^2$
and
![]() $(p^f, p^e) = (2, 4)$
.
$(p^f, p^e) = (2, 4)$
.
Hereafter, assume
![]() $e = f$
. If the RDP is
$e = f$
. If the RDP is
![]() $A_{m-1}$
, then there is nothing to prove. The remaining possibilities are given in Table 4 (Proposition 4.9) and in particular we have
$A_{m-1}$
, then there is nothing to prove. The remaining possibilities are given in Table 4 (Proposition 4.9) and in particular we have
![]() $p \leq 3$
.
$p \leq 3$
.
Assume
![]() $p = 3$
and the RDP is
$p = 3$
and the RDP is
![]() $E_6^1$
or
$E_6^1$
or
![]() $E_8^1$
(as in Proposition 4.9). We may assume that
$E_8^1$
(as in Proposition 4.9). We may assume that
![]() $F = z^2 + x^3 + y^3 + \cdots $
with
$F = z^2 + x^3 + y^3 + \cdots $
with
![]() $\operatorname {\mathrm {wt}}(x,y,z) \equiv (1,-1,0) \pmod {3}$
. Then F cannot be homogeneous since
$\operatorname {\mathrm {wt}}(x,y,z) \equiv (1,-1,0) \pmod {3}$
. Then F cannot be homogeneous since
![]() $\operatorname {\mathrm {wt}}(x^3) \not \equiv \operatorname {\mathrm {wt}}(y^3) \pmod {3^2}$
.
$\operatorname {\mathrm {wt}}(x^3) \not \equiv \operatorname {\mathrm {wt}}(y^3) \pmod {3^2}$
.
Assume
![]() $p = 2$
and the RDP is
$p = 2$
and the RDP is
![]() $D_n$
or
$D_n$
or
![]() $E_n$
. By the classification in Proposition 4.9, we have
$E_n$
. By the classification in Proposition 4.9, we have
![]() $(a,b,c) \equiv (1,1,0) \pmod {2}$
, and
$(a,b,c) \equiv (1,1,0) \pmod {2}$
, and
![]() $F_2 \not \in k z^2$
. If
$F_2 \not \in k z^2$
. If
![]() $(a,b,c) \equiv (1,\pm 1,0) \pmod {4}$
, then
$(a,b,c) \equiv (1,\pm 1,0) \pmod {4}$
, then
![]() $F \in (x,y)^2$
and F cannot define an RDP. If
$F \in (x,y)^2$
and F cannot define an RDP. If
![]() $(a,b,c) \equiv (1,1,2) \pmod {4}$
(then we may assume
$(a,b,c) \equiv (1,1,2) \pmod {4}$
(then we may assume
![]() $F_2 = x^2$
), or if
$F_2 = x^2$
), or if
![]() $(a,b,c) \equiv (1,-1,2) \pmod {4}$
and
$(a,b,c) \equiv (1,-1,2) \pmod {4}$
and
![]() $F_2 = x^2$
, then
$F_2 = x^2$
, then
![]() $F \in (x^2,xyz,xy^3,z^3,z^2y^2,zy^4,y^6)$
and hence F cannot define an RDP. Hence, we may assume
$F \in (x^2,xyz,xy^3,z^3,z^2y^2,zy^4,y^6)$
and hence F cannot define an RDP. Hence, we may assume
![]() $(a,b,c) \equiv (1,-1,2) \pmod {4}$
and
$(a,b,c) \equiv (1,-1,2) \pmod {4}$
and
![]() $F_2 = x^2 + y^2$
, and hence
$F_2 = x^2 + y^2$
, and hence
![]() $p^e = 4$
. If F has
$p^e = 4$
. If F has
![]() $xyz$
, then F must have
$xyz$
, then F must have
![]() $z^{2n-1}$
for some
$z^{2n-1}$
for some
![]() $n \geq 2$
, and then it is
$n \geq 2$
, and then it is
![]() $D_{2n+1}^{n-1}$
. If F does not have
$D_{2n+1}^{n-1}$
. If F does not have
![]() $xyz$
, then F must have
$xyz$
, then F must have
![]() $z^3$
and F must also have
$z^3$
and F must also have
![]() $x^3 y$
or
$x^3 y$
or
![]() $x y^3$
, and then it is
$x y^3$
, and then it is
![]() $E_8^3$
.
$E_8^3$
.
Proposition 4.14. Let
![]() $p \geq 0$
. Let
$p \geq 0$
. Let
![]() $\mathcal {O}_{X,w}$
, together with a
$\mathcal {O}_{X,w}$
, together with a
![]() $\mu _n$
-action (
$\mu _n$
-action (
![]() $n> 1$
), be as in the beginning of §4. Suppose the action fixes w and is symplectic. Then p, n, the type of singularity at w, and the quotient singularity are as in Table 6.
$n> 1$
), be as in the beginning of §4. Suppose the action fixes w and is symplectic. Then p, n, the type of singularity at w, and the quotient singularity are as in Table 6.
Table 6 Symplectic
![]() $\mu _n$
-actions on RDPs.
$\mu _n$
-actions on RDPs.

Proof. If
![]() $p \nmid n$
, then this is Remark 3.5 (Table 2). If
$p \nmid n$
, then this is Remark 3.5 (Table 2). If
![]() $n = p$
, then this is Proposition 4.9 (Table 4). If
$n = p$
, then this is Proposition 4.9 (Table 4). If
![]() $n = p^e$
with
$n = p^e$
with
![]() $e \geq 2$
, then by Proposition 4.13, the possibilities are
$e \geq 2$
, then by Proposition 4.13, the possibilities are
![]() $D_{2n+1}^{n-1}$
,
$D_{2n+1}^{n-1}$
,
![]() $E_8^3$
, and
$E_8^3$
, and
![]() $A_{m-1}$
(with quotient
$A_{m-1}$
(with quotient
![]() $A_{mn-1}$
). In the other cases, we conclude by comparing the tables of the tame case and the
$A_{mn-1}$
). In the other cases, we conclude by comparing the tables of the tame case and the
![]() $n = p$
case. For example,
$n = p$
case. For example,
![]() $E_6^r$
with
$E_6^r$
with
![]() $(p,n) = (3,6)$
is impossible since the
$(p,n) = (3,6)$
is impossible since the
![]() $\mu _2$
-quotient
$\mu _2$
-quotient
![]() $E_7^r$
of
$E_7^r$
of
![]() $E_6^r$
does not admit a symplectic
$E_6^r$
does not admit a symplectic
![]() $\mu _3$
-action.
$\mu _3$
-action.
To a point w fixed by a
![]() $\mu _n$
-action, we define its multiplicity
$\mu _n$
-action, we define its multiplicity
![]() $m(w)$
inductively by:
$m(w)$
inductively by:
-
• if w is a smooth point, then
 $m(w) = 1$
, and
$m(w) = 1$
, and -
• if w is an RDP, then
 $m(w) = \sum _{w' \in \operatorname {\mathrm {Fix}}(\mu _n \curvearrowright \operatorname {\mathrm {Bl}}_w X)} m(w')$
.
$m(w) = \sum _{w' \in \operatorname {\mathrm {Fix}}(\mu _n \curvearrowright \operatorname {\mathrm {Bl}}_w X)} m(w')$
.
The multiplicity for each case is displayed in Table 6. We observe that
![]() $m(\pi _r(w)) = r m(w)$
for any divisor
$m(\pi _r(w)) = r m(w)$
for any divisor
![]() $r < n$
of n, where
$r < n$
of n, where
![]() ${\pi _r}:{X}\to {X/\mu _r}$
is the quotient map and
${\pi _r}:{X}\to {X/\mu _r}$
is the quotient map and
![]() $m(\pi _r(w))$
is the multiplicity with respect to the
$m(\pi _r(w))$
is the multiplicity with respect to the
![]() $\mu _{n/r}$
-action on
$\mu _{n/r}$
-action on
![]() $X/\mu _r$
.
$X/\mu _r$
.
4.4
 $\mu _n$
-actions on smooth points
$\mu _n$
-actions on smooth points
Let
![]() $B = \mathcal {O}_{X,w}$
, together with a
$B = \mathcal {O}_{X,w}$
, together with a
![]() $\mu _n$
-action, be as in the beginning of §4, and assume it is smooth. Assume the
$\mu _n$
-action, be as in the beginning of §4, and assume it is smooth. Assume the
![]() $\mu _n$
-action fixes w and is symplectic at w. As shown in Lemma 4.8(1), there exists
$\mu _n$
-action fixes w and is symplectic at w. As shown in Lemma 4.8(1), there exists
![]() $j \in (\mathbb Z/n\mathbb Z)^*$
, unique up to sign, such that the maximal ideal of B is generated by two homogeneous elements of respective weights j and
$j \in (\mathbb Z/n\mathbb Z)^*$
, unique up to sign, such that the maximal ideal of B is generated by two homogeneous elements of respective weights j and
![]() $-j$
. (We say that the weights of the
$-j$
. (We say that the weights of the
![]() $\mu _n$
-action on the tangent space are j and
$\mu _n$
-action on the tangent space are j and
![]() $-j$
.)
$-j$
.)
Now, let
![]() $\tilde {Y}$
be the minimal resolution of
$\tilde {Y}$
be the minimal resolution of
![]() $Y = X / \mu _n$
at
$Y = X / \mu _n$
at
![]() $\pi (w)$
, and let
$\pi (w)$
, and let
![]() $\pi ' \colon X' = X \times _Y \tilde {Y} \to \tilde {Y}$
. Let
$\pi ' \colon X' = X \times _Y \tilde {Y} \to \tilde {Y}$
. Let
![]() $e_{k}$
(
$e_{k}$
(
![]() $k = 1, \dots , n-1$
) be the exceptional curves of
$k = 1, \dots , n-1$
) be the exceptional curves of
![]() $\tilde {Y}$
, ordered in a way that
$\tilde {Y}$
, ordered in a way that
![]() $e_{k} \cap e_{k'} \neq \emptyset $
if and only if
$e_{k} \cap e_{k'} \neq \emptyset $
if and only if
![]() $\lvert k - k' \rvert \leq 1$
. The
$\lvert k - k' \rvert \leq 1$
. The
![]() $\mu _n$
-action induces a decomposition
$\mu _n$
-action induces a decomposition
![]() $\pi ^{\prime }_* \mathcal {O}_{X'} = \bigoplus _{i \in \mathbb Z/n\mathbb Z} (\pi ^{\prime }_* \mathcal {O}_{X'})_i$
. Let
$\pi ^{\prime }_* \mathcal {O}_{X'} = \bigoplus _{i \in \mathbb Z/n\mathbb Z} (\pi ^{\prime }_* \mathcal {O}_{X'})_i$
. Let
![]() $I_i := \operatorname {\mathrm {Im}}( ((\pi ^{\prime }_* \mathcal {O}_{X'})_i)^{\otimes n} \to \mathcal {O}_{\tilde {Y}})$
for
$I_i := \operatorname {\mathrm {Im}}( ((\pi ^{\prime }_* \mathcal {O}_{X'})_i)^{\otimes n} \to \mathcal {O}_{\tilde {Y}})$
for
![]() $i = 0, \dots , n-1$
. Then
$i = 0, \dots , n-1$
. Then
![]() $I_i$
are described as follows. (Clearly,
$I_i$
are described as follows. (Clearly,
![]() $I_0 = \mathcal {O}_{X'}$
.)
$I_0 = \mathcal {O}_{X'}$
.)
Lemma 4.15.
![]() $(\pi ^{\prime }_* \mathcal {O}_{X'})_i$
and
$(\pi ^{\prime }_* \mathcal {O}_{X'})_i$
and
![]() $I_i$
are invertible sheaves. After possibly reversing the ordering of the exceptional curves, we have an equality
$I_i$
are invertible sheaves. After possibly reversing the ordering of the exceptional curves, we have an equality
 $$\begin{align*}I_i = \mathcal{O}_{\tilde{Y}} \Bigl( -\sum_k f_n \bigl( (j^{-1} i \bmod n), k \bigr) e_k \Bigr), \end{align*}$$
$$\begin{align*}I_i = \mathcal{O}_{\tilde{Y}} \Bigl( -\sum_k f_n \bigl( (j^{-1} i \bmod n), k \bigr) e_k \Bigr), \end{align*}$$
for each
![]() $i = 1, \dots , n-1$
.
$i = 1, \dots , n-1$
.
Here,
![]() $j^{-1} i \bmod n$
denotes the unique integer
$j^{-1} i \bmod n$
denotes the unique integer
![]() $h \in \{0, 1, \dots , n-1\}$
satisfying
$h \in \{0, 1, \dots , n-1\}$
satisfying
![]() $h j \equiv i \pmod {n}$
, and the function
$h j \equiv i \pmod {n}$
, and the function
![]() ${f_n}:{\{1, 2, \dots , n-1\}^2}\to {\mathbb Z}$
is defined as
${f_n}:{\{1, 2, \dots , n-1\}^2}\to {\mathbb Z}$
is defined as
 $$\begin{align*}f_n(h, k) = \begin{cases} h k, & (k \leq n - h), \\ (n - h) (n - k), & (k \geq n - h). \end{cases} \end{align*}$$
$$\begin{align*}f_n(h, k) = \begin{cases} h k, & (k \leq n - h), \\ (n - h) (n - k), & (k \geq n - h). \end{cases} \end{align*}$$
Proof. Straightforward.
5 Tame quotients of K3 surfaces and abelian surfaces
The following fact should be known to experts. (For example, if X is a K3 surface in characteristic
![]() $0$
and G is symplectic and commutative, then this is a result of Nikulin.) We give a proof since we could not find a complete reference (covering all characteristics).
$0$
and G is symplectic and commutative, then this is a result of Nikulin.) We give a proof since we could not find a complete reference (covering all characteristics).
Theorem 5.1. Let X be either an abelian surface or an RDP K3 surface in characteristic
![]() $p \geq 0$
, and G a finite group of order not divisible by p acting on X.
$p \geq 0$
, and G a finite group of order not divisible by p acting on X.
If X is an RDP K3 surface and G is symplectic, then the quotient
![]() $X/G$
is an RDP K3 surface.
$X/G$
is an RDP K3 surface.
If X is an abelian surface and G is symplectic, then
![]() $X/G$
is either an abelian surface or an RDP K3 surface.
$X/G$
is either an abelian surface or an RDP K3 surface.
If X is an RDP K3 surface and G is non-symplectic, then
![]() $X/G$
is either an RDP Enriques surface or a rational surface.
$X/G$
is either an RDP Enriques surface or a rational surface.
If X is an abelian surface and G is non-symplectic, then
![]() $X/G$
is either an RDP Enriques surface, a (quasi-)hyperelliptic surface, a surface birational to a ruled surface, or a rational surface.
$X/G$
is either an RDP Enriques surface, a (quasi-)hyperelliptic surface, a surface birational to a ruled surface, or a rational surface.
Proof. By Proposition 3.4, we may assume X is smooth. Let
![]() ${\pi }:{X}\to {X/G = Y}$
be the quotient morphism, and let
${\pi }:{X}\to {X/G = Y}$
be the quotient morphism, and let
![]() $\tilde {Y} \to Y$
be the minimal resolution.
$\tilde {Y} \to Y$
be the minimal resolution.
We have
![]() $b_1(\tilde {Y}) = b_1(Y) \leq b_1(X)$
, where
$b_1(\tilde {Y}) = b_1(Y) \leq b_1(X)$
, where
![]() $b_i(X) = \dim H_{\mathrm {\acute et}}^i(X, \mathbb Q_l)$
is the ith l-adic Betti number for an auxiliary prime
$b_i(X) = \dim H_{\mathrm {\acute et}}^i(X, \mathbb Q_l)$
is the ith l-adic Betti number for an auxiliary prime
![]() $l \neq \operatorname {\mathrm {char}} k$
. Hence, if X is a K3 surface (hence
$l \neq \operatorname {\mathrm {char}} k$
. Hence, if X is a K3 surface (hence
![]() $b_1(X) = 0$
), then
$b_1(X) = 0$
), then
![]() $\tilde {Y}$
cannot be abelian, (quasi-)hyperelliptic, nor nonrational ruled.
$\tilde {Y}$
cannot be abelian, (quasi-)hyperelliptic, nor nonrational ruled.
First, suppose G acts non-symplectically. If some nontrivial
![]() $g \in G$
satisfy
$g \in G$
satisfy
![]() $\dim \operatorname {\mathrm {Fix}}(g) = 1$
, then by the usual ramification formula,
$\dim \operatorname {\mathrm {Fix}}(g) = 1$
, then by the usual ramification formula,
![]() $K_Y$
has negative coefficients at the corresponding divisors of Y, and hence
$K_Y$
has negative coefficients at the corresponding divisors of Y, and hence
![]() $\kappa (\tilde {Y}) = -\infty $
. If Y has a non-RDP singularity, then
$\kappa (\tilde {Y}) = -\infty $
. If Y has a non-RDP singularity, then
![]() $K_{\tilde {Y}}$
has negative coefficients at the corresponding exceptional curves, and hence
$K_{\tilde {Y}}$
has negative coefficients at the corresponding exceptional curves, and hence
![]() $\kappa (\tilde {Y}) = -\infty $
. In either case,
$\kappa (\tilde {Y}) = -\infty $
. In either case,
![]() $\tilde {Y}$
is either ruled or rational. Suppose neither is the case. Then
$\tilde {Y}$
is either ruled or rational. Suppose neither is the case. Then
![]() $K_Y$
is an RDP surface with numerically trivial
$K_Y$
is an RDP surface with numerically trivial
![]() $K_Y$
. Since we have
$K_Y$
. Since we have
![]() $K_Y$
is not trivial. Then, by the classification of such surfaces (see Table 1),
$K_Y$
is not trivial. Then, by the classification of such surfaces (see Table 1),
![]() $\tilde {Y}$
is either an Enriques surface or a (quasi-)hyperelliptic surface. This settles the non-symplectic case.
$\tilde {Y}$
is either an Enriques surface or a (quasi-)hyperelliptic surface. This settles the non-symplectic case.
Now, suppose G acts symplectically. By Proposition 3.4, Y is an RDP surface with
![]() $K_Y$
trivial. By the classification of surfaces with trivial canonical divisor, Y is an RDP K3 surface, an abelian surface, a non-classical RDP Enriques surface (
$K_Y$
trivial. By the classification of surfaces with trivial canonical divisor, Y is an RDP K3 surface, an abelian surface, a non-classical RDP Enriques surface (
![]() $p = 2$
), or a (quasi-)hyperelliptic surface (
$p = 2$
), or a (quasi-)hyperelliptic surface (
![]() $p = 2,3$
). (Note that abelian and (quasi-)hyperelliptic surface admit no smooth rational curves.)
$p = 2,3$
). (Note that abelian and (quasi-)hyperelliptic surface admit no smooth rational curves.)
Since Y has only RDP singularities, we have
![]() $h^1(\tilde {Y}, \mathcal {O}_{\tilde {Y}}) = h^1(Y, \mathcal {O}_Y)$
. Since
$h^1(\tilde {Y}, \mathcal {O}_{\tilde {Y}}) = h^1(Y, \mathcal {O}_Y)$
. Since
![]() $p \nmid \lvert G \rvert $
,
$p \nmid \lvert G \rvert $
,
![]() $(\mathcal {O}_X)^G \subset \mathcal {O}_X$
is a direct summand and hence we have
$(\mathcal {O}_X)^G \subset \mathcal {O}_X$
is a direct summand and hence we have
![]() $h^1(Y, \mathcal {O}_Y) = h^1(Y, (\pi _* \mathcal {O}_X)^G) \leq h^1(Y, \pi _* \mathcal {O}_X) = h^1(X, \mathcal {O}_X)$
. Therefore, if X is a K3 surface, then Y cannot be a nonclassical RDP Enriques surface.
$h^1(Y, \mathcal {O}_Y) = h^1(Y, (\pi _* \mathcal {O}_X)^G) \leq h^1(Y, \pi _* \mathcal {O}_X) = h^1(X, \mathcal {O}_X)$
. Therefore, if X is a K3 surface, then Y cannot be a nonclassical RDP Enriques surface.
It remains to show that if X is an abelian surface, then Y cannot be a (quasi-)hyperelliptic surface. (If
![]() $p \neq 2,3$
, then this is clear since (quasi-)hyperelliptic surfaces always have nontrivial canonical divisor.) If X is an abelian surface and Y is a (quasi-)hyperelliptic surface, then since a (quasi-)hyperelliptic surface admits no smooth rational curves, no element of
$p \neq 2,3$
, then this is clear since (quasi-)hyperelliptic surfaces always have nontrivial canonical divisor.) If X is an abelian surface and Y is a (quasi-)hyperelliptic surface, then since a (quasi-)hyperelliptic surface admits no smooth rational curves, no element of
![]() $G \setminus \{1\}$
has fixed points. It suffices to show that any fixed-point-free symplectic automorphism g of an abelian surface X of finite order not divisible by p is a translation, since the quotient of an abelian variety by a finite group of translations is an abelian variety.
$G \setminus \{1\}$
has fixed points. It suffices to show that any fixed-point-free symplectic automorphism g of an abelian surface X of finite order not divisible by p is a translation, since the quotient of an abelian variety by a finite group of translations is an abelian variety.
Suppose g is such an automorphism. Endow X with a group variety structure (i.e., choose an origin) and write
![]() $g(x) = h(x) + a$
with h an automorphism of the group variety (i.e., h fixes the origin) and a a point. Then h is symplectic (since g and the translation by a are symplectic) and of finite order dividing
$g(x) = h(x) + a$
with h an automorphism of the group variety (i.e., h fixes the origin) and a a point. Then h is symplectic (since g and the translation by a are symplectic) and of finite order dividing
![]() $\operatorname {\mathrm {ord}}(g)$
, since
$\operatorname {\mathrm {ord}}(g)$
, since
![]() $x = g^{\operatorname {\mathrm {ord}}(g)}(x) = h^{\operatorname {\mathrm {ord}}(g)}(x) + (h^{\operatorname {\mathrm {ord}}(g)-1}(a) + \dots + a)$
. If
$x = g^{\operatorname {\mathrm {ord}}(g)}(x) = h^{\operatorname {\mathrm {ord}}(g)}(x) + (h^{\operatorname {\mathrm {ord}}(g)-1}(a) + \dots + a)$
. If
![]() $h = \mathrm {id}$
, then g is a translation. Suppose
$h = \mathrm {id}$
, then g is a translation. Suppose
![]() $h \neq \mathrm {id}$
. Then h acts on the tangent space of each fixed point via
$h \neq \mathrm {id}$
. Then h acts on the tangent space of each fixed point via
![]() $\operatorname {\mathrm {SL}}_2(k)$
(since h is symplectic and of finite order not divisible by p), and hence
$\operatorname {\mathrm {SL}}_2(k)$
(since h is symplectic and of finite order not divisible by p), and hence
![]() $\operatorname {\mathrm {Fix}}(h)$
is isolated. Hence,
$\operatorname {\mathrm {Fix}}(h)$
is isolated. Hence,
![]() $h - \mathrm {id}$
has finite kernel and hence is surjective. Let x be a point with
$h - \mathrm {id}$
has finite kernel and hence is surjective. Let x be a point with
![]() $h(x) - x = - a$
. Then
$h(x) - x = - a$
. Then
![]() $g(x) = x$
, contradiction.
$g(x) = x$
, contradiction.
6
 $\mu _p$
-quotients of RDP K3 surfaces and abelian surfaces
$\mu _p$
-quotients of RDP K3 surfaces and abelian surfaces
The following theorems are the
![]() $\mu _p$
-analogue of Theorem 5.1.
$\mu _p$
-analogue of Theorem 5.1.
Theorem 6.1. The quotient of an RDP K3 surface by a symplectic
![]() $\mu _{p}$
-action is again an RDP K3 surface.
$\mu _{p}$
-action is again an RDP K3 surface.
Theorem 6.2. The quotient
![]() $X/\mu _p$
of an RDP K3 surface by a non-symplectic action of
$X/\mu _p$
of an RDP K3 surface by a non-symplectic action of
![]() $\mu _p$
is either a rational surface (possibly with non-RDP singularities) or an RDP Enriques surface. The quotient is an RDP Enriques surface if and only if the action is fixed-point-free, and this can happen only if
$\mu _p$
is either a rational surface (possibly with non-RDP singularities) or an RDP Enriques surface. The quotient is an RDP Enriques surface if and only if the action is fixed-point-free, and this can happen only if
![]() $p = 2$
.
$p = 2$
.
Theorem 6.3. A
![]() $\mu _{p^e}$
-action on an abelian variety is always symplectic, in the sense that the one-dimensional space of top differential forms is of weight
$\mu _{p^e}$
-action on an abelian variety is always symplectic, in the sense that the one-dimensional space of top differential forms is of weight
![]() $0$
, and the quotient is again an abelian surface.
$0$
, and the quotient is again an abelian surface.
Proof of Theorem 6.3
It suffices to consider
![]() $\mu _p$
-actions. A
$\mu _p$
-actions. A
![]() $\mu _p$
-action on A corresponds [Reference SeshadriGP, Th. VII.7.2(ii)] to an element
$\mu _p$
-action on A corresponds [Reference SeshadriGP, Th. VII.7.2(ii)] to an element
![]() $v \in H^0(A, T) \cong T_0 A$
satisfying
$v \in H^0(A, T) \cong T_0 A$
satisfying
![]() $v^p = v$
, and hence the action can be identified with the translation action by a subgroup scheme of A. Then the quotient is again an abelian variety, and hence this action is symplectic by Proposition 2.10.
$v^p = v$
, and hence the action can be identified with the translation action by a subgroup scheme of A. Then the quotient is again an abelian variety, and hence this action is symplectic by Proposition 2.10.
Proof of Theorem 6.1
By Theorem 4.6(1,2),
![]() $Y = X/\mu _p$
is an RDP surface. Then, by Proposition 2.10,
$Y = X/\mu _p$
is an RDP surface. Then, by Proposition 2.10,
![]() $K_{Y}$
is trivial, and by the classification of surfaces, Y is either an RDP K3 surface, an abelian surface, a nonclassical RDP Enriques surface, or a (quasi-)hyperelliptic surface.
$K_{Y}$
is trivial, and by the classification of surfaces, Y is either an RDP K3 surface, an abelian surface, a nonclassical RDP Enriques surface, or a (quasi-)hyperelliptic surface.
Since
![]() ${\pi }:{X}\to {Y}$
is purely inseparable, we have
${\pi }:{X}\to {Y}$
is purely inseparable, we have
![]() $\dim H_{\mathrm {\acute et}}^i(X, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^i(Y, \mathbb Q_l)$
, in particular
$\dim H_{\mathrm {\acute et}}^i(X, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^i(Y, \mathbb Q_l)$
, in particular
![]() $b_1(Y) = b_1(X) = 0$
(where
$b_1(Y) = b_1(X) = 0$
(where
![]() $b_i = \dim H_{\mathrm {\acute et}}^i$
is the ith Betti number). Since Y is an RDP surface and since
$b_i = \dim H_{\mathrm {\acute et}}^i$
is the ith Betti number). Since Y is an RDP surface and since
![]() $\mathcal {O}_Y = (\pi _* \mathcal {O}_X)_0$
is a direct summand of
$\mathcal {O}_Y = (\pi _* \mathcal {O}_X)_0$
is a direct summand of
![]() $\pi _* \mathcal {O}_X$
, we have
$\pi _* \mathcal {O}_X$
, we have
![]() $h^1(\tilde {Y}, \mathcal {O}_{\tilde {Y}}) = h^1(Y, \mathcal {O}_Y) \leq h^1(Y, \pi _* \mathcal {O}_X) = h^1(X, \mathcal {O}_X) = 0$
. Hence, Y is an RDP K3 surface.
$h^1(\tilde {Y}, \mathcal {O}_{\tilde {Y}}) = h^1(Y, \mathcal {O}_Y) \leq h^1(Y, \pi _* \mathcal {O}_X) = h^1(X, \mathcal {O}_X) = 0$
. Hence, Y is an RDP K3 surface.
Proof of Theorem 6.2
Let X be an RDP K3 surface equipped with a nontrivial non-symplectic
![]() $\mu _p$
-action. Let
$\mu _p$
-action. Let
![]() $Y = X/\mu _p$
. We have
$Y = X/\mu _p$
. We have
![]() $b_1(Y) = b_1(X) = 0$
, and hence as in the tame case (§5), the minimal resolution
$b_1(Y) = b_1(X) = 0$
, and hence as in the tame case (§5), the minimal resolution
![]() $\tilde {Y}$
of Y cannot be abelian, (quasi-)hyperelliptic, nor non-rational ruled.
$\tilde {Y}$
of Y cannot be abelian, (quasi-)hyperelliptic, nor non-rational ruled.
If D has non-isolated fixed points, then by the Rudakov–Shafarevich formula
![]() $K_X \sim (p-1) (D) + \pi ^* K_Y$
[Reference OgusRS, Cor. 1 to Prop. 3], or by Proposition 2.10,
$K_X \sim (p-1) (D) + \pi ^* K_Y$
[Reference OgusRS, Cor. 1 to Prop. 3], or by Proposition 2.10,
![]() $\kappa (\tilde {Y}) = -\infty $
. If D has an isolated fixed point
$\kappa (\tilde {Y}) = -\infty $
. If D has an isolated fixed point
![]() $w \in X$
, then by Theorem 4.6(3),
$w \in X$
, then by Theorem 4.6(3),
![]() $\pi (w) \in Y$
is a non-RDP singularity, and then hence
$\pi (w) \in Y$
is a non-RDP singularity, and then hence
![]() $\kappa (\tilde {Y}) = -\infty $
. In either case, Y is a rational surface.
$\kappa (\tilde {Y}) = -\infty $
. In either case, Y is a rational surface.
Now, assume D is fixed-point-free. Then, by Theorem 4.6(1), Y is an RDP surface and, by the Rudakov–Shafarevich formula,
![]() $K_{Y}$
is torsion. Moreover, it follows from Proposition 2.10 that the space
$K_{Y}$
is torsion. Moreover, it follows from Proposition 2.10 that the space
![]() $H^0(Y^{\mathrm {sm}}, (\Omega ^2)^{\otimes n})$
is
$H^0(Y^{\mathrm {sm}}, (\Omega ^2)^{\otimes n})$
is
![]() $0$
if
$0$
if
![]() $0 < n < p$
and is generated by a nonvanishing multicanonical form if
$0 < n < p$
and is generated by a nonvanishing multicanonical form if
![]() $n = p$
. Thus,
$n = p$
. Thus,
![]() $K_{\tilde {Y}}$
is nonzero and p-torsion. By the classification of surfaces, it follows that Y is an RDP Enriques surface. Then, since
$K_{\tilde {Y}}$
is nonzero and p-torsion. By the classification of surfaces, it follows that Y is an RDP Enriques surface. Then, since
![]() $2K_{Y} \sim 0$
and
$2K_{Y} \sim 0$
and
![]() $H^0(Y^{\mathrm {sm}}, \mathcal {O}(n K_{Y})) = 0$
for
$H^0(Y^{\mathrm {sm}}, \mathcal {O}(n K_{Y})) = 0$
for
![]() $0 < n < p$
, we have
$0 < n < p$
, we have
![]() $p = 2$
.
$p = 2$
.
There is also the following relation with the height of K3 surfaces. The height is an invariant of a K3 surface in positive characteristic which is either
![]() $\infty $
or an integer in
$\infty $
or an integer in
![]() $\{1, \dots , 10\}$
. See §8 for more details.
$\{1, \dots , 10\}$
. See §8 for more details.
Corollary 6.4. Let X be an RDP K3 surface in characteristic p equipped with a nontrivial
![]() $\mu _p$
-action. If X is of finite height, then the action is symplectic and the quotient is an RDP K3 surface.
$\mu _p$
-action. If X is of finite height, then the action is symplectic and the quotient is an RDP K3 surface.
Proof. We assume that the action is non-symplectic and show that then X is not of finite height. By Theorem 6.2, the quotient
![]() $Y = X / \mu _p$
is a rational surface or an RDP Enriques surface. Hence, X admits a purely inseparable finite morphism
$Y = X / \mu _p$
is a rational surface or an RDP Enriques surface. Hence, X admits a purely inseparable finite morphism
![]() ${Y}^{(1/p)} \to X$
from a rational surface or an RDP Enriques surface. Hence,
${Y}^{(1/p)} \to X$
from a rational surface or an RDP Enriques surface. Hence,
![]() $H_{\mathrm {\acute et}}^2(X, \mathbb Q_l)$
, which is isomorphic to
$H_{\mathrm {\acute et}}^2(X, \mathbb Q_l)$
, which is isomorphic to
![]() $H^2({Y}^{(1/p)}, \mathbb Q_l)$
, is generated by algebraic cycles, which is impossible if X is of finite height by Lemma 8.3(2).
$H^2({Y}^{(1/p)}, \mathbb Q_l)$
, is generated by algebraic cycles, which is impossible if X is of finite height by Lemma 8.3(2).
Remark 6.5. In a subsequent paper [Reference MatsumotoMat4, Th. 1.3], we prove that also the converse holds, and we moreover determine the height in terms of the singularities of X and Y.
We call a proper birational morphism
![]() $X' \to X$
between RDP surfaces to be a partial resolution if it is dominated by the minimal resolution
$X' \to X$
between RDP surfaces to be a partial resolution if it is dominated by the minimal resolution
![]() $\tilde {X}$
of X. The following proposition often enables us to reduce assertions on
$\tilde {X}$
of X. The following proposition often enables us to reduce assertions on
![]() $\mu _p$
-actions to simpler cases.
$\mu _p$
-actions to simpler cases.
Proposition 6.6. Let X be an RDP surface equipped with a
![]() $\mu _p$
-action.
$\mu _p$
-action.
-
1. Among partial resolutions of X to which the
 $\mu _p$
-action extends, there exists a unique maximal one, which we call the maximal partial resolution of X.
$\mu _p$
-action extends, there exists a unique maximal one, which we call the maximal partial resolution of X. -
2. A partial resolution
 $X' \to X$
is maximal if and only if it satisfies the property
$X' \to X$
is maximal if and only if it satisfies the property
 $\operatorname {\mathrm {Sing}}(X') \cap \pi ^{-1}(\operatorname {\mathrm {Sing}}(X'/\mu _p)) = \emptyset $
.
$\operatorname {\mathrm {Sing}}(X') \cap \pi ^{-1}(\operatorname {\mathrm {Sing}}(X'/\mu _p)) = \emptyset $
. -
3. The action on X is fixed-point-free if and only if the action on the maximal partial resolution is fixed-point-free.
-
4. Suppose X is an RDP K3 surface. The action on X is symplectic if and only if the action on the maximal partial resolution is symplectic.
We say that an RDP surface X equipped with a
![]() $\mu _p$
-action is maximal if it is the maximal partial resolution of itself.
$\mu _p$
-action is maximal if it is the maximal partial resolution of itself.
Proof. Note that isomorphism classes of partial resolutions are in one-to-one correspondence to subsets of the set of exceptional curves of
![]() $\tilde {X} \to X$
.
$\tilde {X} \to X$
.
(1) Let
![]() $X'$
be a partial resolution. Let
$X'$
be a partial resolution. Let
![]() $\tilde {D}$
and
$\tilde {D}$
and
![]() $D'$
be the rational derivations induced by D on
$D'$
be the rational derivations induced by D on
![]() $\tilde {X}$
and
$\tilde {X}$
and
![]() $X'$
. Clearly,
$X'$
. Clearly,
![]() $D'$
is regular and thus corresponds to a
$D'$
is regular and thus corresponds to a
![]() $\mu _p$
-action if and only if the coefficient of
$\mu _p$
-action if and only if the coefficient of
![]() $(D')$
for each exceptional curve of
$(D')$
for each exceptional curve of
![]() $X' \to X$
is nonnegative. Therefore, the contraction of all exceptional curves on
$X' \to X$
is nonnegative. Therefore, the contraction of all exceptional curves on
![]() $\tilde {X}$
with negative coefficients in
$\tilde {X}$
with negative coefficients in
![]() $(\tilde {D})$
is the maximal partial resolution.
$(\tilde {D})$
is the maximal partial resolution.
(2) First, suppose
![]() $X'$
does not satisfy the property. There is an RDP
$X'$
does not satisfy the property. There is an RDP
![]() $w \in X'$
such that
$w \in X'$
such that
![]() $\pi (w)$
is not smooth. If w is a fixed RDP, then let
$\pi (w)$
is not smooth. If w is a fixed RDP, then let
![]() $X^{\prime }_1 = \operatorname {\mathrm {Bl}}_w X'$
. If w is a non-fixed RDP, then let
$X^{\prime }_1 = \operatorname {\mathrm {Bl}}_w X'$
. If w is a non-fixed RDP, then let
![]() $X^{\prime }_1 = X' \times _{Y'} Y^{\prime }_1$
, where
$X^{\prime }_1 = X' \times _{Y'} Y^{\prime }_1$
, where
![]() $Y'$
is the
$Y'$
is the
![]() $\mu _p$
-quotient of
$\mu _p$
-quotient of
![]() $X'$
and
$X'$
and
![]() $Y^{\prime }_1 \to Y'$
is the minimal resolution at
$Y^{\prime }_1 \to Y'$
is the minimal resolution at
![]() $\pi (w)$
. Then the
$\pi (w)$
. Then the
![]() $\mu _p$
-action extends to
$\mu _p$
-action extends to
![]() $X^{\prime }_1$
(by Proposition 2.8 in the former case, clear in the latter case) and
$X^{\prime }_1$
(by Proposition 2.8 in the former case, clear in the latter case) and
![]() $X^{\prime }_1$
is a partial resolution of
$X^{\prime }_1$
is a partial resolution of
![]() $X'$
(clear in the former case, by Theorem 4.6(1) in the latter case). Thus,
$X'$
(clear in the former case, by Theorem 4.6(1) in the latter case). Thus,
![]() $X'$
is not maximal.
$X'$
is not maximal.
Conversely, suppose
![]() $X'$
satisfies the property. Let
$X'$
satisfies the property. Let
![]() $w \in \operatorname {\mathrm {Sing}}(X')$
. To show that
$w \in \operatorname {\mathrm {Sing}}(X')$
. To show that
![]() $X'$
is maximal, it suffices to show that every exceptional curve of
$X'$
is maximal, it suffices to show that every exceptional curve of
![]() $\tilde {X}$
above w appears in
$\tilde {X}$
above w appears in
![]() $(\tilde {D})$
with negative coefficient, since then it must be contracted in the maximal partial resolution. This follows from the Rudakov–Shafarevich formula
$(\tilde {D})$
with negative coefficient, since then it must be contracted in the maximal partial resolution. This follows from the Rudakov–Shafarevich formula
![]() $K_{\tilde {X}} \sim (p-1) (\tilde {D}) + \pi ^* K_{\tilde {Y}}$
[Reference OgusRS, Cor. 1 to Prop. 3], where
$K_{\tilde {X}} \sim (p-1) (\tilde {D}) + \pi ^* K_{\tilde {Y}}$
[Reference OgusRS, Cor. 1 to Prop. 3], where
![]() $\tilde {Y} = \tilde {X}/\mu _p$
: for each exceptional curve, its coefficient in
$\tilde {Y} = \tilde {X}/\mu _p$
: for each exceptional curve, its coefficient in
![]() $K_{\tilde {X}}$
(resp.
$K_{\tilde {X}}$
(resp.
![]() $\pi ^* K_{\tilde {Y}}$
) is
$\pi ^* K_{\tilde {Y}}$
) is
![]() $0$
(resp. positive) since
$0$
(resp. positive) since
![]() $\tilde {X}$
is the minimal resolution of the RDP w (resp. since
$\tilde {X}$
is the minimal resolution of the RDP w (resp. since
![]() $\pi (w)$
is a smooth point). Alternatively, one can use the explicit computation of
$\pi (w)$
is a smooth point). Alternatively, one can use the explicit computation of
![]() $(\tilde {D})$
given in Lemma 6.7. (w is non-fixed since
$(\tilde {D})$
given in Lemma 6.7. (w is non-fixed since
![]() $\pi (w)$
is a smooth point [Theorem 4.6(2,3)].)
$\pi (w)$
is a smooth point [Theorem 4.6(2,3)].)
We also observe that the maximal partial resolution of X can be constructed by repeatedly applying the procedure of constructing
![]() $X_1'$
from
$X_1'$
from
![]() $X'$
. Indeed, the total index of RDPs strictly decreases through the procedure.
$X'$
. Indeed, the total index of RDPs strictly decreases through the procedure.
(3) It suffices to show that the procedure above preserves the (non-)fixed-point-freeness. If w is a non-fixed RDP, then there is no fixed point above w by the functoriality of the fixed-point scheme. If w is a fixed RDP, then there is a fixed point above w by Corollary 2.12.
(4) The spaces of
![]() $2$
-forms in question are naturally isomorphic.
$2$
-forms in question are naturally isomorphic.
Lemma 6.7. Let X be an RDP surface, and let D be a derivation of multiplicative type. Let
![]() $w \in X$
be a non-fixed RDP of index n, and suppose the image of w is a smooth point. Let
$w \in X$
be a non-fixed RDP of index n, and suppose the image of w is a smooth point. Let
![]() $\tilde X$
be the minimal resolution at w, and let
$\tilde X$
be the minimal resolution at w, and let
![]() $\tilde D$
be the induced rational derivation on
$\tilde D$
be the induced rational derivation on
![]() $\tilde X$
. Let
$\tilde X$
. Let
![]() $(\tilde {D})$
and
$(\tilde {D})$
and
![]() $\langle \tilde {D} \rangle $
be the divisorial and isolated fixed locus of
$\langle \tilde {D} \rangle $
be the divisorial and isolated fixed locus of
![]() $\tilde D$
above w. Then every exceptional curve of
$\tilde D$
above w. Then every exceptional curve of
![]() $\tilde {X}$
above w appears in
$\tilde {X}$
above w appears in
![]() $(\tilde {D})$
with negative coefficient, and we have
$(\tilde {D})$
with negative coefficient, and we have
![]() $\deg \langle \tilde {D} \rangle = \frac {p-2}{p-1} n$
and
$\deg \langle \tilde {D} \rangle = \frac {p-2}{p-1} n$
and
![]() $(\tilde {D})^2 = - \frac {2}{p-1} n$
.
$(\tilde {D})^2 = - \frac {2}{p-1} n$
.
Proof. We compute
![]() $(\tilde {D})$
and
$(\tilde {D})$
and
![]() $\langle \tilde {D} \rangle $
by a straightforward calculation using the classification of non-fixed RDPs given in Proposition 4.7. See [Reference MatsumotoMat3, Lem. 3.11] for the result. Then the assertions follow.
$\langle \tilde {D} \rangle $
by a straightforward calculation using the classification of non-fixed RDPs given in Proposition 4.7. See [Reference MatsumotoMat3, Lem. 3.11] for the result. Then the assertions follow.
Proposition 6.8. Suppose each of X and Y is either an RDP K3 surface or an RDP Enriques surface. Let
![]() $\pi \colon X \to Y$
be a
$\pi \colon X \to Y$
be a
![]() $\mu _p$
-quotient morphism. Suppose X is maximal with respect to the
$\mu _p$
-quotient morphism. Suppose X is maximal with respect to the
![]() $\mu _p$
-action. Then the total index
$\mu _p$
-action. Then the total index
![]() $N_1$
of non-fixed RDPs and the number
$N_1$
of non-fixed RDPs and the number
![]() $N_2$
of fixed points on X are as follows:
$N_2$
of fixed points on X are as follows:
 $$\begin{align*}(N_1, N_2) = \begin{cases} (24 \frac{p-1}{p+1}, 24 \frac{1}{p+1}), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{K3},\mathrm{K3}), \\ (12 \frac{2p-1}{p+1}, 12 \frac{p-2}{p^2-1}) = (12, 0), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{K3},\mathrm{Enr}), \\ (12 \frac{p-2}{p+1}, 12 \frac{2p-1}{p^2-1}) = (0, 12), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{Enr},\mathrm{K3}), \\ (12 \frac{p-1}{p+1}, 12 \frac{1}{p+1}), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{Enr},\mathrm{Enr}). \\ \end{cases} \end{align*}$$
$$\begin{align*}(N_1, N_2) = \begin{cases} (24 \frac{p-1}{p+1}, 24 \frac{1}{p+1}), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{K3},\mathrm{K3}), \\ (12 \frac{2p-1}{p+1}, 12 \frac{p-2}{p^2-1}) = (12, 0), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{K3},\mathrm{Enr}), \\ (12 \frac{p-2}{p+1}, 12 \frac{2p-1}{p^2-1}) = (0, 12), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{Enr},\mathrm{K3}), \\ (12 \frac{p-1}{p+1}, 12 \frac{1}{p+1}), & \text{if } (\tilde X, \tilde Y) \text{ is } (\mathrm{Enr},\mathrm{Enr}). \\ \end{cases} \end{align*}$$
In the cases where
![]() $(\tilde {X}, \tilde {Y})$
is
$(\tilde {X}, \tilde {Y})$
is
![]() $(\mathrm {K3}, \mathrm {Enr})$
or
$(\mathrm {K3}, \mathrm {Enr})$
or
![]() $(\mathrm {Enr}, \mathrm {K3})$
, only
$(\mathrm {Enr}, \mathrm {K3})$
, only
![]() $p = 2$
is possible.
$p = 2$
is possible.
Proof. Let D be the corresponding derivation of multiplicative type. Since
![]() $\tilde {Y}$
is of Kodaira dimension
$\tilde {Y}$
is of Kodaira dimension
![]() $0$
,
$0$
,
![]() $\operatorname {\mathrm {Fix}}(D)$
consists only of isolated points (possibly none).
$\operatorname {\mathrm {Fix}}(D)$
consists only of isolated points (possibly none).
Define the rational derivation
![]() $\tilde D$
on
$\tilde D$
on
![]() $\tilde {X}$
as in Lemma 6.7. Since the fixed locus of
$\tilde {X}$
as in Lemma 6.7. Since the fixed locus of
![]() $\tilde D$
consists of those above non-fixed RDPs on X and the
$\tilde D$
consists of those above non-fixed RDPs on X and the
![]() $0$
-cycle of fixed points on X, by Lemma 6.7, we have
$0$
-cycle of fixed points on X, by Lemma 6.7, we have
 $$\begin{align*}(\tilde{D})^2 = - \frac{2}{p-1} N_1, \quad \deg \langle \tilde{D} \rangle = N_2 + \frac{p-2}{p-1} N_1, \end{align*}$$
$$\begin{align*}(\tilde{D})^2 = - \frac{2}{p-1} N_1, \quad \deg \langle \tilde{D} \rangle = N_2 + \frac{p-2}{p-1} N_1, \end{align*}$$
and by the Katsura–Takeda formula (Proposition 2.13), we have
 $$\begin{align*}\deg c_2(\tilde{X}) = (N_2 + \frac{p-2}{p-1} N_1) + 0 + \frac{2}{p-1} N_1 = N_2 + \frac{p}{p-1} N_1. \end{align*}$$
$$\begin{align*}\deg c_2(\tilde{X}) = (N_2 + \frac{p-2}{p-1} N_1) + 0 + \frac{2}{p-1} N_1 = N_2 + \frac{p}{p-1} N_1. \end{align*}$$
On the other hand, we have
![]() $\dim H_{\mathrm {\acute et}}^2(X, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^2(\tilde {X}, \mathbb Q_l) - N_1 = b_2(\tilde {X}) - N_1$
. Since Y is an RDP surface whose RDPs are precisely the images (which are
$\dim H_{\mathrm {\acute et}}^2(X, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^2(\tilde {X}, \mathbb Q_l) - N_1 = b_2(\tilde {X}) - N_1$
. Since Y is an RDP surface whose RDPs are precisely the images (which are
![]() $A_{p-1}$
) of the fixed smooth points of X, we have
$A_{p-1}$
) of the fixed smooth points of X, we have
![]() $\dim H_{\mathrm {\acute et}}^2(Y, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^2(\tilde {Y}, \mathbb Q_l) - (p-1)N_2 = b_2(\tilde {Y}) - (p-1)N_2$
. Since
$\dim H_{\mathrm {\acute et}}^2(Y, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^2(\tilde {Y}, \mathbb Q_l) - (p-1)N_2 = b_2(\tilde {Y}) - (p-1)N_2$
. Since
![]() $X \to Y$
is purely inseparable, we have
$X \to Y$
is purely inseparable, we have
![]() $\dim H_{\mathrm {\acute et}}^2(X, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^2(Y, \mathbb Q_l)$
. Therefore, we have
$\dim H_{\mathrm {\acute et}}^2(X, \mathbb Q_l) = \dim H_{\mathrm {\acute et}}^2(Y, \mathbb Q_l)$
. Therefore, we have
![]() $(p-1) N_2 - N_1 = b_2(\tilde {Y}) - b_2(\tilde {X})$
.
$(p-1) N_2 - N_1 = b_2(\tilde {Y}) - b_2(\tilde {X})$
.
Combining the two equalities, we determine
![]() $(N_1,N_2)$
in terms of p. In two cases, only
$(N_1,N_2)$
in terms of p. In two cases, only
![]() $p = 2$
is possible since
$p = 2$
is possible since
![]() $12 \frac {p-2}{p^2-1}$
or
$12 \frac {p-2}{p^2-1}$
or
![]() $12 \frac {2p-1}{p^2-1}$
must be an integer.
$12 \frac {2p-1}{p^2-1}$
must be an integer.
7 Possible orders of symplectic
 $\mu _n$
-actions on RDP K3 surfaces
$\mu _n$
-actions on RDP K3 surfaces
The following theorem is again parallel to the case of automorphisms of finite tame order, but the proof (for
![]() $\mu _p$
-actions) is quite different.
$\mu _p$
-actions) is quite different.
Theorem 7.1. Let X be an RDP K3 surface in characteristic p equipped with a symplectic
![]() $\mu _{n}$
-action (
$\mu _{n}$
-action (
![]() $n> 1$
, divisible by p or not). Then:
$n> 1$
, divisible by p or not). Then:
-
1.
 $n \leq 8$
.
$n \leq 8$
. -
2. The number of fixed points, counted with the multiplicities defined after Proposition 4.14, depends only on n and is as in Table 7.
Table 7 Symplectic
 $\mu _n$
-actions on K3 surfaces.
$\mu _n$
-actions on K3 surfaces.
-
3. Assume all fixed points are smooth points. Then the decomposition of
 $\bigoplus _{w \in \operatorname {\mathrm {Fix}}(\mu _n)} T^*_w X$
with respect to the
$\bigoplus _{w \in \operatorname {\mathrm {Fix}}(\mu _n)} T^*_w X$
with respect to the
 $\mu _n$
-action is concentrated on the subset
$\mu _n$
-action is concentrated on the subset
 $(\mathbb Z/n\mathbb Z)^* \subset \mathbb Z/n\mathbb Z$
, and for every
$(\mathbb Z/n\mathbb Z)^* \subset \mathbb Z/n\mathbb Z$
, and for every
 $i \in (\mathbb Z/n\mathbb Z)^*$
, the ith summand has dimension as in Table 7.
$i \in (\mathbb Z/n\mathbb Z)^*$
, the ith summand has dimension as in Table 7.
If
![]() $p \nmid n$
(resp. if
$p \nmid n$
(resp. if
![]() $n = p$
), then assertion (3) means that every primitive nth root of
$n = p$
), then assertion (3) means that every primitive nth root of
![]() $1$
(resp. every element of
$1$
(resp. every element of
![]() $\mathbb F_p^*$
) appears as an eigenvalue of a fixed generator of
$\mathbb F_p^*$
) appears as an eigenvalue of a fixed generator of
![]() $\mu _n \cong \mathbb Z/n\mathbb Z$
(resp. of the corresponding derivation) on the space
$\mu _n \cong \mathbb Z/n\mathbb Z$
(resp. of the corresponding derivation) on the space
![]() $\bigoplus _{w \in \operatorname {\mathrm {Fix}}(\mu _n)} T^*_w X$
with equal multiplicity.
$\bigoplus _{w \in \operatorname {\mathrm {Fix}}(\mu _n)} T^*_w X$
with equal multiplicity.
For each p and each
![]() $n \leq 8$
, there indeed exists an RDP K3 surface equipped with a symplectic
$n \leq 8$
, there indeed exists an RDP K3 surface equipped with a symplectic
![]() $\mu _{n}$
-action in characteristic p. See §9.1 for explicit examples.
$\mu _{n}$
-action in characteristic p. See §9.1 for explicit examples.
Proof of Theorem 7.1 for the case
 $p \nmid n$
$p \nmid n$
We may assume X is smooth.
Assertions (1) and (2) are proved by Nikulin [Reference MukaiNi, §5] (
![]() $p = 0$
) and Dolgachev–Keum [Reference Dolgachev and KeumDK2, Th. 3.3] (
$p = 0$
) and Dolgachev–Keum [Reference Dolgachev and KeumDK2, Th. 3.3] (
![]() $p> 0$
). (Both proofs overlooked the case
$p> 0$
). (Both proofs overlooked the case
![]() $n = 14$
, but their arguments for the nonexistence of the case
$n = 14$
, but their arguments for the nonexistence of the case
![]() $n = 15$
apply to case
$n = 15$
apply to case
![]() $n = 14$
.)
$n = 14$
.)
(3) (If
![]() $p = 0$
, then this follows from the argument in [Reference MatsumotoMu, Prop. 1.2]. We give another proof, applicable to all
$p = 0$
, then this follows from the argument in [Reference MatsumotoMu, Prop. 1.2]. We give another proof, applicable to all
![]() $p \geq 0$
.)
$p \geq 0$
.)
Let
![]() $w \in X$
, and let
$w \in X$
, and let
![]() $\mu _r = \operatorname {\mathrm {Stab}}(w) \subset \mu _n$
be its stabilizer group. Suppose the decomposition of
$\mu _r = \operatorname {\mathrm {Stab}}(w) \subset \mu _n$
be its stabilizer group. Suppose the decomposition of
![]() $T^*_w X$
(
$T^*_w X$
(
![]() $ = \mathfrak {m}_w / \mathfrak {m}_w^2$
) with respect to the
$ = \mathfrak {m}_w / \mathfrak {m}_w^2$
) with respect to the
![]() $\mu _r$
-action is concentrated on two (not necessarily distinct) weights
$\mu _r$
-action is concentrated on two (not necessarily distinct) weights
![]() $j_1, j_2 \in \mathbb Z/r\mathbb Z$
. Then since the action on
$j_1, j_2 \in \mathbb Z/r\mathbb Z$
. Then since the action on
![]() $\Omega ^2_{X,w} \cong \bigwedge ^2 T^*_w X$
is trivial, we have
$\Omega ^2_{X,w} \cong \bigwedge ^2 T^*_w X$
is trivial, we have
![]() $j_1 + j_2 = 0$
. We have
$j_1 + j_2 = 0$
. We have
![]() $j_1,j_2 \in (\mathbb Z/r\mathbb Z)^*$
, since if
$j_1,j_2 \in (\mathbb Z/r\mathbb Z)^*$
, since if
![]() $\gcd (j_1, r) = \gcd (j_2, r) = r'> 1$
, then
$\gcd (j_1, r) = \gcd (j_2, r) = r'> 1$
, then
![]() $\mu _{r'}$
acts trivially, contradicting the assumption that the action is faithful. This already proves the assertion if
$\mu _{r'}$
acts trivially, contradicting the assumption that the action is faithful. This already proves the assertion if
![]() $n = 2,3,4,6$
, since up to sign there is only one element in
$n = 2,3,4,6$
, since up to sign there is only one element in
![]() $(\mathbb Z/n\mathbb Z)^*$
.
$(\mathbb Z/n\mathbb Z)^*$
.
For each divisor
![]() $r \neq 1$
of n and for each
$r \neq 1$
of n and for each
![]() $0 \leq j \leq \lfloor r/2 \rfloor $
, let
$0 \leq j \leq \lfloor r/2 \rfloor $
, let
![]() $S_{r,j}$
be the set of the points
$S_{r,j}$
be the set of the points
![]() $w \in X$
with
$w \in X$
with
![]() $\operatorname {\mathrm {Stab}}(w) = \mu _r$
and with
$\operatorname {\mathrm {Stab}}(w) = \mu _r$
and with
![]() $\mu _r$
acting on
$\mu _r$
acting on
![]() $T^*_w X$
by weights j and
$T^*_w X$
by weights j and
![]() $-j$
. Then
$-j$
. Then
![]() $S_{r,j}$
is a finite set and it is empty if
$S_{r,j}$
is a finite set and it is empty if
![]() $j \not \in (\mathbb Z/r\mathbb Z)^*$
. Let
$j \not \in (\mathbb Z/r\mathbb Z)^*$
. Let
![]() $\tilde {S}_{r,j} = S_{r,j} / \mu _n$
be the set of
$\tilde {S}_{r,j} = S_{r,j} / \mu _n$
be the set of
![]() $\mu _n$
-orbits of points of
$\mu _n$
-orbits of points of
![]() $S_{r,j}$
. Let
$S_{r,j}$
. Let
![]() $N_{r,j} = \lvert S_{r,j} \rvert $
and
$N_{r,j} = \lvert S_{r,j} \rvert $
and
![]() $\tilde {N}_{r,j} = \lvert \tilde {S}_{r,j} \rvert = N_{r,j} / (n/r)$
.
$\tilde {N}_{r,j} = \lvert \tilde {S}_{r,j} \rvert = N_{r,j} / (n/r)$
.
Let
![]() ${\rho }:{\tilde {Y}}\to {Y = X / \mu _n}$
be the minimal resolution (then
${\rho }:{\tilde {Y}}\to {Y = X / \mu _n}$
be the minimal resolution (then
![]() $\tilde {Y}$
is a smooth K3 surface), and let
$\tilde {Y}$
is a smooth K3 surface), and let
![]() $\pi ' \colon X' = X \times _Y \tilde {Y} \to \tilde {Y}$
. Let
$\pi ' \colon X' = X \times _Y \tilde {Y} \to \tilde {Y}$
. Let
![]() $\pi ^{\prime }_* \mathcal {O}_{X'} = \bigoplus _{i \in \mathbb Z/n\mathbb Z} (\pi ^{\prime }_* \mathcal {O}_{X'})_i$
be the decomposition induced by the
$\pi ^{\prime }_* \mathcal {O}_{X'} = \bigoplus _{i \in \mathbb Z/n\mathbb Z} (\pi ^{\prime }_* \mathcal {O}_{X'})_i$
be the decomposition induced by the
![]() $\mu _n$
-action. Then, by Lemma 4.15,
$\mu _n$
-action. Then, by Lemma 4.15,
![]() $(\pi ^{\prime }_* \mathcal {O}_{X'})_i$
are invertible sheaves, and they are described as follows. For each
$(\pi ^{\prime }_* \mathcal {O}_{X'})_i$
are invertible sheaves, and they are described as follows. For each
![]() $i \in \mathbb Z/n\mathbb Z$
, let
$i \in \mathbb Z/n\mathbb Z$
, let
![]() $C_i$
be the corresponding class of Cartier divisors. For each orbit
$C_i$
be the corresponding class of Cartier divisors. For each orbit
![]() $w \in \tilde {S}_{r,j}$
, its image
$w \in \tilde {S}_{r,j}$
, its image
![]() $\pi (w)$
is an RDP of type
$\pi (w)$
is an RDP of type
![]() $A_{r-1}$
, and let
$A_{r-1}$
, and let
![]() $e_{w,k}$
(
$e_{w,k}$
(
![]() $k = 1, \dots , r-1$
) be the exceptional curves in
$k = 1, \dots , r-1$
) be the exceptional curves in
![]() $\tilde {Y}$
above
$\tilde {Y}$
above
![]() $\pi (w)$
, ordered in a way that
$\pi (w)$
, ordered in a way that
![]() $e_{w,k} \cap e_{w,k'} \neq \emptyset $
if and only if
$e_{w,k} \cap e_{w,k'} \neq \emptyset $
if and only if
![]() $\lvert k - k' \rvert \leq 1$
. Then, after possibly reversing the ordering, we have a linear equivalence
$\lvert k - k' \rvert \leq 1$
. Then, after possibly reversing the ordering, we have a linear equivalence
 $$\begin{align*}- r C_i \sim \sum_{r \mid n, r \neq 1} \sum_{j = 0}^{\lfloor r/2 \rfloor} \sum_{w \in \tilde{S}_{r,j}} \sum_{k = 1}^{r-1} {f_r(({j^{-1}} i \bmod r), k)} e_{w,k} \end{align*}$$
$$\begin{align*}- r C_i \sim \sum_{r \mid n, r \neq 1} \sum_{j = 0}^{\lfloor r/2 \rfloor} \sum_{w \in \tilde{S}_{r,j}} \sum_{k = 1}^{r-1} {f_r(({j^{-1}} i \bmod r), k)} e_{w,k} \end{align*}$$
(see Lemma 4.15 for the definition of the function
![]() ${f_r}:{\{1, \dots , r-1\}^2}\to {\mathbb Z}$
) for each
${f_r}:{\{1, \dots , r-1\}^2}\to {\mathbb Z}$
) for each
![]() $i \neq 0$
.
$i \neq 0$
.
Let m be any integer with
![]() $1 \leq m \leq r-1$
. Using the equality
$1 \leq m \leq r-1$
. Using the equality
 $$\begin{align*}\Biggl( \sum_{k=1}^{r-1} \frac{f_r(m,k)}{r} e_{w,k} \Biggr) \cdot e_{w,k'} = \begin{cases} -1, & \text{if } k' = r - m, \\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\Biggl( \sum_{k=1}^{r-1} \frac{f_r(m,k)}{r} e_{w,k} \Biggr) \cdot e_{w,k'} = \begin{cases} -1, & \text{if } k' = r - m, \\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
we compute that
 $$\begin{align*}\Biggl( \sum_{k=1}^{r-1} \frac{f_r(m,k)}{r} e_{w,k} \Biggr)^2 = -\frac{m(r-m)}{r}. \end{align*}$$
$$\begin{align*}\Biggl( \sum_{k=1}^{r-1} \frac{f_r(m,k)}{r} e_{w,k} \Biggr)^2 = -\frac{m(r-m)}{r}. \end{align*}$$
Hence, we have
 $$\begin{align*}- C_i^2 = \sum_{r \mid n, r \neq 1} \sum_{j = 0}^{\lfloor r/2 \rfloor} \tilde{N}_{r,j} \cdot \frac{({j^{-1}}i \bmod r)(r - {j^{-1}}i \bmod r)}{r} \end{align*}$$
$$\begin{align*}- C_i^2 = \sum_{r \mid n, r \neq 1} \sum_{j = 0}^{\lfloor r/2 \rfloor} \tilde{N}_{r,j} \cdot \frac{({j^{-1}}i \bmod r)(r - {j^{-1}}i \bmod r)}{r} \end{align*}$$
and this must belong to
![]() $2 \mathbb Z$
.
$2 \mathbb Z$
.
Assume
![]() $n = 5$
. Then we have
$n = 5$
. Then we have
![]() $N_{5,j} = \tilde {N}_{5,j}$
,
$N_{5,j} = \tilde {N}_{5,j}$
,
![]() $N_{5,1} + N_{5,2} = 4$
, and
$N_{5,1} + N_{5,2} = 4$
, and
Hence,
![]() $(N_{5,1}, N_{5,2}) = (2, 2)$
.
$(N_{5,1}, N_{5,2}) = (2, 2)$
.
Assume
![]() $n = 7$
. Then we have
$n = 7$
. Then we have
![]() $N_{7,j} = \tilde {N}_{7,j}$
,
$N_{7,j} = \tilde {N}_{7,j}$
,
![]() $N_{7,1} + N_{7,2} + N_{7,3} = 3$
, and
$N_{7,1} + N_{7,2} + N_{7,3} = 3$
, and
Hence,
![]() $(N_{7,1}, N_{7,2}, N_{7,3}) = (1, 1, 1)$
.
$(N_{7,1}, N_{7,2}, N_{7,3}) = (1, 1, 1)$
.
Assume
![]() $n = 8$
. By assertion (2) for the cases
$n = 8$
. By assertion (2) for the cases
![]() $n = 2,4,8$
, we have
$n = 2,4,8$
, we have
![]() $\tilde {N}_{2,1} = 1$
,
$\tilde {N}_{2,1} = 1$
,
![]() $\tilde {N}_{4,1} = 1$
,
$\tilde {N}_{4,1} = 1$
,
![]() $\tilde {N}_{8,1} + \tilde {N}_{8,3} = 2$
, and
$\tilde {N}_{8,1} + \tilde {N}_{8,3} = 2$
, and
Hence,
![]() $({N}_{8,1}, {N}_{8,3}) = (\tilde {N}_{8,1}, \tilde {N}_{8,3}) = (1, 1)$
.
$({N}_{8,1}, {N}_{8,3}) = (\tilde {N}_{8,1}, \tilde {N}_{8,3}) = (1, 1)$
.
Remark 7.2. By above, we have
![]() $C_i^2 = -4$
for any
$C_i^2 = -4$
for any
![]() $2 \leq n \leq 8$
and any
$2 \leq n \leq 8$
and any
![]() $1 \leq i \leq n-1$
. As we see below, this holds also if p divides n. This implies
$1 \leq i \leq n-1$
. As we see below, this holds also if p divides n. This implies
![]() $\chi (\tilde {Y}, (\pi ^{\prime }_* \mathcal {O}_{X'})_i) = 0$
for
$\chi (\tilde {Y}, (\pi ^{\prime }_* \mathcal {O}_{X'})_i) = 0$
for
![]() $i \neq 0$
. Then we obtain
$i \neq 0$
. Then we obtain
![]() $\chi (Y, (\pi _* \mathcal {O}_{X})_i) = 0$
for
$\chi (Y, (\pi _* \mathcal {O}_{X})_i) = 0$
for
![]() $i \neq 0$
, since
$i \neq 0$
, since
![]() $\rho _*((\pi ^{\prime }_* \mathcal {O}_{X'})_i) = (\pi _* \mathcal {O}_{X'})_i$
and
$\rho _*((\pi ^{\prime }_* \mathcal {O}_{X'})_i) = (\pi _* \mathcal {O}_{X'})_i$
and
![]() $R^q \rho _*((\pi ^{\prime }_* \mathcal {O}_{X'})_i) = 0$
for
$R^q \rho _*((\pi ^{\prime }_* \mathcal {O}_{X'})_i) = 0$
for
![]() $q> 0$
. This is finer than the equality
$q> 0$
. This is finer than the equality
 $$\begin{align*}\sum_{i \neq 0} \chi(Y, (\pi_* \mathcal{O}_{X})_i) = \chi(X, \mathcal{O}_X) - \chi(Y, \mathcal{O}_Y) = 2 - 2 = 0. \end{align*}$$
$$\begin{align*}\sum_{i \neq 0} \chi(Y, (\pi_* \mathcal{O}_{X})_i) = \chi(X, \mathcal{O}_X) - \chi(Y, \mathcal{O}_Y) = 2 - 2 = 0. \end{align*}$$
Proof of Theorem 7.1 for the case
 $n = p$
$n = p$
We may assume that X is maximal. (For assertion (2), the multiplicity is by definition compatible with blowups at fixed points.) This means that all fixed points are smooth points, and that the singularities of the quotient surface Y are all
![]() $A_{p-1}$
and are precisely the images of the fixed points. Let D be the corresponding derivation.
$A_{p-1}$
and are precisely the images of the fixed points. Let D be the corresponding derivation.
As in the previous case, let
![]() $\tilde {Y}$
be the minimal resolution of Y (hence a smooth K3 surface) and let
$\tilde {Y}$
be the minimal resolution of Y (hence a smooth K3 surface) and let
![]() $\pi ' \colon X' = X \times _Y \tilde {Y} \to \tilde {Y}$
. The sheaf
$\pi ' \colon X' = X \times _Y \tilde {Y} \to \tilde {Y}$
. The sheaf
![]() $\pi ^{\prime }_* \mathcal {O}_{X'}$
admits a decomposition to invertible sheaves
$\pi ^{\prime }_* \mathcal {O}_{X'}$
admits a decomposition to invertible sheaves
![]() $(\pi ^{\prime }_* \mathcal {O}_{X'})_i$
. For each
$(\pi ^{\prime }_* \mathcal {O}_{X'})_i$
. For each
![]() $i \in \mathbb Z/p\mathbb Z$
, let
$i \in \mathbb Z/p\mathbb Z$
, let
![]() $C_i$
be the corresponding class of Cartier divisor. As in the previous case, we have
$C_i$
be the corresponding class of Cartier divisor. As in the previous case, we have
 $$\begin{align*}- C_i^2 = \sum_{j = 0}^{\lfloor p/2 \rfloor} N_{p,j} \cdot \frac{({j^{-1}}i \bmod p)(p - {j^{-1}}i \bmod p)}{p}. \end{align*}$$
$$\begin{align*}- C_i^2 = \sum_{j = 0}^{\lfloor p/2 \rfloor} N_{p,j} \cdot \frac{({j^{-1}}i \bmod p)(p - {j^{-1}}i \bmod p)}{p}. \end{align*}$$
By Proposition 6.8, we have
![]() $N := \sum _{j} N_{p,j} = 24/(p+1)$
. Hence,
$N := \sum _{j} N_{p,j} = 24/(p+1)$
. Hence,
![]() $p \in \{2,3,5,7,11,23\}$
. If
$p \in \{2,3,5,7,11,23\}$
. If
![]() $p = 23,$
then
$p = 23,$
then
![]() $N = 1$
and the exceptional curves generate a negative definite sublattice of rank
$N = 1$
and the exceptional curves generate a negative definite sublattice of rank
![]() $p-1 = 22$
of the indefinite lattice
$p-1 = 22$
of the indefinite lattice
![]() $\operatorname {\mathrm {Pic}}(\tilde {Y})$
of rank
$\operatorname {\mathrm {Pic}}(\tilde {Y})$
of rank
![]() $\leq 22$
, contradiction. If
$\leq 22$
, contradiction. If
![]() $p = 11$
, then
$p = 11$
, then
![]() $N = 2$
and then
$N = 2$
and then
![]() $C_i^2$
(for any
$C_i^2$
(for any
![]() $i \in (\mathbb Z/p\mathbb Z)^*$
) cannot be an integer since the sum of two nonzero squares in
$i \in (\mathbb Z/p\mathbb Z)^*$
) cannot be an integer since the sum of two nonzero squares in
![]() $\mathbb F_{11}$
cannot be zero. Hence, we have
$\mathbb F_{11}$
cannot be zero. Hence, we have
![]() $p \in \{2,3,5,7\}$
, and we can determine the multiplicities of the weights as in the
$p \in \{2,3,5,7\}$
, and we can determine the multiplicities of the weights as in the
![]() $p \nmid n$
case.
$p \nmid n$
case.
Corollary 7.3. Let X be an RDP K3 surface equipped with a symplectic
![]() $\mu _{q}$
-action with
$\mu _{q}$
-action with
![]() $q = 5,7$
. Here, both
$q = 5,7$
. Here, both
![]() $p = q$
and
$p = q$
and
![]() $p \neq q$
are allowed.
$p \neq q$
are allowed.
-
• If
 $q = 7$
, then any fixed point is a smooth point.
$q = 7$
, then any fixed point is a smooth point. -
• If
 $q = 5$
, then any fixed point is a smooth point or an RDP of type
$q = 5$
, then any fixed point is a smooth point or an RDP of type
 $A_1$
.
$A_1$
.
Proof. Let
![]() $w \in X$
be a fixed point. By Proposition 4.14, w is of type
$w \in X$
be a fixed point. By Proposition 4.14, w is of type
![]() $A_{m-1}$
for some
$A_{m-1}$
for some
![]() $m \geq 1$
. Let
$m \geq 1$
. Let
![]() $\pm i \in (\mathbb Z/q\mathbb Z)^*$
be the nonzero weights of
$\pm i \in (\mathbb Z/q\mathbb Z)^*$
be the nonzero weights of
![]() $\mathfrak {m}_w/\mathfrak {m}_w^2$
with respect to the
$\mathfrak {m}_w/\mathfrak {m}_w^2$
with respect to the
![]() $\mu _q$
-action. Let
$\mu _q$
-action. Let
![]() $\tilde {X}$
be the minimal resolution of X at w (to which the
$\tilde {X}$
be the minimal resolution of X at w (to which the
![]() $\mu _q$
-action extends). One can calculate the local equation to show that all (smooth) fixed point of
$\mu _q$
-action extends). One can calculate the local equation to show that all (smooth) fixed point of
![]() $\tilde {X}$
above w has weights
$\tilde {X}$
above w has weights
![]() $\pm i$
. Since there are m such points, it follows from Theorem 7.1(3) that
$\pm i$
. Since there are m such points, it follows from Theorem 7.1(3) that
![]() $m \leq 1$
if
$m \leq 1$
if
![]() $q = 7$
and
$q = 7$
and
![]() $m \leq 2$
if
$m \leq 2$
if
![]() $q = 5$
.
$q = 5$
.
Proof of Theorem 7.1 for the case
 $n = p^e$
(
$n = p^e$
(
 $e \geq 2$
)
$e \geq 2$
)
For each
![]() $0 \leq j \leq e$
, let
$0 \leq j \leq e$
, let
![]() $\pi _j \colon X \to X_j = X/\mu _{p^j}$
be the quotient morphism by the subgroup scheme
$\pi _j \colon X \to X_j = X/\mu _{p^j}$
be the quotient morphism by the subgroup scheme
![]() $\mu _{p^j} \subset \mu _{p^e}$
, and for each
$\mu _{p^j} \subset \mu _{p^e}$
, and for each
![]() $0 \leq j \leq e-1$
, let
$0 \leq j \leq e-1$
, let
![]() $D_j$
be the derivation on
$D_j$
be the derivation on
![]() $X_j$
corresponding to the action of
$X_j$
corresponding to the action of
![]() $\mu _{p^{j+1}}/\mu _{p^j}$
.
$\mu _{p^{j+1}}/\mu _{p^j}$
.
Let
![]() $w \in X$
be a
$w \in X$
be a
![]() $\mu _p$
-fixed point. Let
$\mu _p$
-fixed point. Let
![]() $\mu _{p^f} = \operatorname {\mathrm {Stab}}(w)$
(then
$\mu _{p^f} = \operatorname {\mathrm {Stab}}(w)$
(then
![]() $1 \leq f \leq e$
). Then, by Remark 4.4,
$1 \leq f \leq e$
). Then, by Remark 4.4,
![]() $\mu _{p^f}$
acts symplectically at w. By Proposition 4.13, either w is of type
$\mu _{p^f}$
acts symplectically at w. By Proposition 4.13, either w is of type
![]() $A_{m-1}$
for some
$A_{m-1}$
for some
![]() $m \geq 1$
with
$m \geq 1$
with
![]() $p^{e-f} \mid m$
, or w is
$p^{e-f} \mid m$
, or w is
![]() $D_{2m+1}^{m-1}$
or
$D_{2m+1}^{m-1}$
or
![]() $E_7^2$
or
$E_7^2$
or
![]() $E_8^3$
and
$E_8^3$
and
![]() $p^e = 4$
. (Again, we use the convention that a smooth point is of type
$p^e = 4$
. (Again, we use the convention that a smooth point is of type
![]() $A_0$
.) Then since each
$A_0$
.) Then since each
![]() $D_j$
(
$D_j$
(
![]() $j < f$
) is symplectic at
$j < f$
) is symplectic at
![]() $\pi _j(w)$
, we observe that
$\pi _j(w)$
, we observe that
![]() $\pi _f(w) \in X_f$
is of type
$\pi _f(w) \in X_f$
is of type
![]() $A_{p^e m - 1}$
or
$A_{p^e m - 1}$
or
![]() $D_5^0$
or
$D_5^0$
or
![]() $D_{2m+1}^{m-1}$
. (Since X has a
$D_{2m+1}^{m-1}$
. (Since X has a
![]() $\mu _p$
-fixed point and since
$\mu _p$
-fixed point and since
![]() $X_f$
is an RDP K3 surface, this already implies
$X_f$
is an RDP K3 surface, this already implies
![]() $p^e - 1 < 22$
.)
$p^e - 1 < 22$
.)
By Lemma 4.11, any preimage of any fixed point of
![]() $D_{j}$
is again fixed. In other words, the fixed points of
$D_{j}$
is again fixed. In other words, the fixed points of
![]() $D_j$
on
$D_j$
on
![]() $X_j$
are precisely the images of the
$X_j$
are precisely the images of the
![]() $\mu _{p^{j+1}}$
-fixed points on X.
$\mu _{p^{j+1}}$
-fixed points on X.
For each
![]() $1 \leq f \leq e$
, let
$1 \leq f \leq e$
, let
![]() $\tilde {S}_f \subset X$
be the points with stabilizer equal to
$\tilde {S}_f \subset X$
be the points with stabilizer equal to
![]() $\mu _{p^f}$
. For each
$\mu _{p^f}$
. For each
![]() $w \in \tilde {S}_f$
, let
$w \in \tilde {S}_f$
, let
![]() $m(w)$
be its multiplicity of w defined after Proposition 4.14 with respect to the
$m(w)$
be its multiplicity of w defined after Proposition 4.14 with respect to the
![]() $\mu _{p^f}$
-action. Then, by Propositions 4.13 and 4.14, we have
$\mu _{p^f}$
-action. Then, by Propositions 4.13 and 4.14, we have
![]() $p^{e-f} \mid m(w)$
. Let
$p^{e-f} \mid m(w)$
. Let
![]() $M_f = \sum _{w \in \tilde {S}_f} m(w)$
for each
$M_f = \sum _{w \in \tilde {S}_f} m(w)$
for each
![]() $1 \leq f \leq e$
, then by above
$1 \leq f \leq e$
, then by above
![]() $p^{e-f} \mid M_f$
. Using the equality mentioned after Proposition 4.14 and assertion (2) for
$p^{e-f} \mid M_f$
. Using the equality mentioned after Proposition 4.14 and assertion (2) for
![]() $D_{e-1}$
and
$D_{e-1}$
and
![]() $D_{e-2}$
on
$D_{e-2}$
on
![]() $X_{e-1}$
and
$X_{e-1}$
and
![]() $X_{e-2}$
, we obtain
$X_{e-2}$
, we obtain
![]() $p^{e-1} M_e = p^{e-2} (M_e + M_{e-1}) = 24/(p+1)$
, and hence
$p^{e-1} M_e = p^{e-2} (M_e + M_{e-1}) = 24/(p+1)$
, and hence
![]() $M_e = 24 / (p^{e-1}(p+1))$
and
$M_e = 24 / (p^{e-1}(p+1))$
and
![]() $M_{e-1} / p = 24 (p-1) / (p^{e}(p+1))$
. Since
$M_{e-1} / p = 24 (p-1) / (p^{e}(p+1))$
. Since
![]() $M_{e-1} / p$
is an integer,
$M_{e-1} / p$
is an integer,
![]() $p^e$
divides
$p^e$
divides
![]() $24$
. Therefore,
$24$
. Therefore,
![]() $p^e = 2^2, 2^3$
. Moreover, we obtain
$p^e = 2^2, 2^3$
. Moreover, we obtain
![]() $M_f = p^{e-f} \cdot 24 (p-1) / (p^{e}(p+1))$
(
$M_f = p^{e-f} \cdot 24 (p-1) / (p^{e}(p+1))$
(
![]() $1 \leq f \leq e-1$
) by applying assertion (2) to
$1 \leq f \leq e-1$
) by applying assertion (2) to
![]() $D_{j}$
(
$D_{j}$
(
![]() $0 \leq j \leq e-1$
).
$0 \leq j \leq e-1$
).
Assertion (3) is trivial if
![]() $n = 4$
. Suppose
$n = 4$
. Suppose
![]() $n = 8$
. For each
$n = 8$
. For each
![]() $1 \leq f \leq 3$
and
$1 \leq f \leq 3$
and
![]() $0 \leq j \leq 2^f/2$
, let
$0 \leq j \leq 2^f/2$
, let
![]() $\tilde {S}_{2^f,j}$
be the set of the points with stabilizer
$\tilde {S}_{2^f,j}$
be the set of the points with stabilizer
![]() $\mu _{2^f}$
and with primitive weights
$\mu _{2^f}$
and with primitive weights
![]() $\pm j \in (\mathbb Z/2^f\mathbb Z)^*$
, and let
$\pm j \in (\mathbb Z/2^f\mathbb Z)^*$
, and let
![]() $\tilde {N}_{2^f,j} = (2^{e-f})^{-1} \sum _{w \in \tilde {S}_{2^f,j}} m(w)$
. We have
$\tilde {N}_{2^f,j} = (2^{e-f})^{-1} \sum _{w \in \tilde {S}_{2^f,j}} m(w)$
. We have
![]() $\sum _{j} \tilde {N}_{2^f,j} = (2^{e-f})^{-1} M_f$
for each
$\sum _{j} \tilde {N}_{2^f,j} = (2^{e-f})^{-1} M_f$
for each
![]() $1 \leq~f~\leq~e$
. Then we again have
$1 \leq~f~\leq~e$
. Then we again have
![]() $\tilde {N}_{2,1} = 1$
,
$\tilde {N}_{2,1} = 1$
,
![]() $\tilde {N}_{4,1} = 1$
,
$\tilde {N}_{4,1} = 1$
,
![]() $\tilde {N}_{8,1} + \tilde {N}_{8,3} = 2$
, and
$\tilde {N}_{8,1} + \tilde {N}_{8,3} = 2$
, and
Hence,
![]() $(\tilde {N}_{8,1}, \tilde {N}_{8,3}) = (1,1)$
.
$(\tilde {N}_{8,1}, \tilde {N}_{8,3}) = (1,1)$
.
Proof of Theorem 7.1 for the remaining cases
First, we show that if
![]() $n = pq$
where q is a prime
$n = pq$
where q is a prime
![]() $\neq p$
, then
$\neq p$
, then
![]() $n = 6$
. We have
$n = 6$
. We have
![]() $\mu _n = \mu _p \times \mu _q \cong \mu _p \times \mathbb Z/q\mathbb Z$
. We may assume that X is maximal with respect to the
$\mu _n = \mu _p \times \mu _q \cong \mu _p \times \mathbb Z/q\mathbb Z$
. We may assume that X is maximal with respect to the
![]() $\mu _p$
-action. Let
$\mu _p$
-action. Let
![]() $\pi _q \colon X \to X_q = X / \mu _q$
and
$\pi _q \colon X \to X_q = X / \mu _q$
and
![]() $\pi _p \colon X \to X_p = X / \mu _p$
. Note that
$\pi _p \colon X \to X_p = X / \mu _p$
. Note that
![]() $w \in X$
is fixed by the
$w \in X$
is fixed by the
![]() $\mu _p$
-action if and only if
$\mu _p$
-action if and only if
![]() $\pi _q(w) \in X_q$
is fixed by the
$\pi _q(w) \in X_q$
is fixed by the
![]() $\mu _p$
-action. Let
$\mu _p$
-action. Let
![]() $a_1$
and
$a_1$
and
![]() $a_q$
be the number of
$a_q$
be the number of
![]() $\mu _q$
-orbits of length
$\mu _q$
-orbits of length
![]() $1$
and q of
$1$
and q of
![]() $\mu _p$
-fixed points of X (which are all smooth by assumption). Then the
$\mu _p$
-fixed points of X (which are all smooth by assumption). Then the
![]() $\mu _p$
-fixed points of
$\mu _p$
-fixed points of
![]() $X_q$
consists of
$X_q$
consists of
![]() $a_1$
points of type
$a_1$
points of type
![]() $A_{q-1}$
and
$A_{q-1}$
and
![]() $a_q$
smooth points. Applying assertion (2) to the
$a_q$
smooth points. Applying assertion (2) to the
![]() $\mu _p$
-actions on X and
$\mu _p$
-actions on X and
![]() $X_q$
we have
$X_q$
we have
![]() $a_1 + q a_q = q a_1 + a_q = 24/(p+1)$
. Therefore,
$a_1 + q a_q = q a_1 + a_q = 24/(p+1)$
. Therefore,
![]() $a_1 = a_q = 24/(p+1)(q+1)$
and hence
$a_1 = a_q = 24/(p+1)(q+1)$
and hence
![]() $(a_1, \{p, q \}) = (2, \{2, 3 \}), (1, \{2, 7 \} ), (1, \{3, 5 \})$
.
$(a_1, \{p, q \}) = (2, \{2, 3 \}), (1, \{2, 7 \} ), (1, \{3, 5 \})$
.
The cases
![]() $(a_1, \{p, q \}) = (1, \{2, 7 \} ), (1, \{3, 5 \})$
are impossible since letting
$(a_1, \{p, q \}) = (1, \{2, 7 \} ), (1, \{3, 5 \})$
are impossible since letting
![]() $w \in X$
be the unique
$w \in X$
be the unique
![]() $\mu _{pq}$
-fixed point (which is a smooth point), if
$\mu _{pq}$
-fixed point (which is a smooth point), if
![]() $pq = 14$
then
$pq = 14$
then
![]() $\pi _2(w) \in X_2$
is a
$\pi _2(w) \in X_2$
is a
![]() $\mu _7$
-fixed RDP of type
$\mu _7$
-fixed RDP of type
![]() $A_{1}$
, and if
$A_{1}$
, and if
![]() $pq = 15$
then
$pq = 15$
then
![]() $\pi _3(w) \in X_3$
is a
$\pi _3(w) \in X_3$
is a
![]() $\mu _5$
-fixed RDP of type
$\mu _5$
-fixed RDP of type
![]() $A_{2}$
, both contradicting Corollary 7.3.
$A_{2}$
, both contradicting Corollary 7.3.
Now, we consider general n. It remains to show that the cases
![]() $(p,n) = (2,12), (3,12)$
are impossible.
$(p,n) = (2,12), (3,12)$
are impossible.
Assume
![]() $(p,n) = (3,12)$
. As above, we may assume X is maximal with respect to the
$(p,n) = (3,12)$
. As above, we may assume X is maximal with respect to the
![]() $\mu _3$
-action. There are exactly six
$\mu _3$
-action. There are exactly six
![]() $\mu _3$
-fixed points, all smooth. By the above argument for
$\mu _3$
-fixed points, all smooth. By the above argument for
![]() $(p,n) = (3,6)$
, exactly two of them are
$(p,n) = (3,6)$
, exactly two of them are
![]() $\mu _2$
-fixed, and among the images of these two points in
$\mu _2$
-fixed, and among the images of these two points in
![]() $X/\mu _2$
, exactly one is
$X/\mu _2$
, exactly one is
![]() $(\mu _4/\mu _2)$
-fixed. This is impossible since non-
$(\mu _4/\mu _2)$
-fixed. This is impossible since non-
![]() $(\mu _4/\mu _2)$
-fixed points in
$(\mu _4/\mu _2)$
-fixed points in
![]() $X / \mu _2$
come by pairs.
$X / \mu _2$
come by pairs.
Now, assume
![]() $(p,n) = (2,12)$
. As in the proof of the
$(p,n) = (2,12)$
. As in the proof of the
![]() $n = p^e$
case (applied to the
$n = p^e$
case (applied to the
![]() $\mu _4$
-action), let
$\mu _4$
-action), let
![]() $\tilde {S}_1$
be the set of
$\tilde {S}_1$
be the set of
![]() $\mu _2$
-fixed non-
$\mu _2$
-fixed non-
![]() $\mu _4$
-fixed points, and then we have
$\mu _4$
-fixed points, and then we have
![]() $M_1 = \sum _{w \in \tilde {S}_1} m(w) = 4$
and
$M_1 = \sum _{w \in \tilde {S}_1} m(w) = 4$
and
![]() $2 \mid m(w)$
. Hence,
$2 \mid m(w)$
. Hence,
![]() $\lvert \tilde {S}_1 \rvert $
is
$\lvert \tilde {S}_1 \rvert $
is
![]() $1$
or
$1$
or
![]() $2$
. Since the
$2$
. Since the
![]() $\mu _3$
-action on X preserves this
$\mu _3$
-action on X preserves this
![]() $1$
- or
$1$
- or
![]() $2$
-point set
$2$
-point set
![]() $\tilde {S}_1$
, it acts on
$\tilde {S}_1$
, it acts on
![]() $\tilde {S}_1$
trivially, and hence fixes at least four
$\tilde {S}_1$
trivially, and hence fixes at least four
![]() $\mu _2$
-fixed points (counted with multiplicity
$\mu _2$
-fixed points (counted with multiplicity
![]() $m(w)$
), contradicting the observation
$m(w)$
), contradicting the observation
![]() $a_1 = 2$
for
$a_1 = 2$
for
![]() $\mu _6$
-actions.
$\mu _6$
-actions.
Assertion (3) for
![]() $n = 6$
is trivial.
$n = 6$
is trivial.
8 Possible orders of
 $\mu _n$
-actions on RDP K3 surfaces
$\mu _n$
-actions on RDP K3 surfaces
Let
![]() $S_{\mathrm {cyc}}(p)$
(resp.
$S_{\mathrm {cyc}}(p)$
(resp.
![]() $S_{\mu }(p)$
) be the set of positive integers n for which there exists an RDP K3 surface equipped with an automorphism of order n (resp. a
$S_{\mu }(p)$
) be the set of positive integers n for which there exists an RDP K3 surface equipped with an automorphism of order n (resp. a
![]() $\mu _n$
-action) in characteristic p. We clearly have
$\mu _n$
-action) in characteristic p. We clearly have
![]() $S_{\mathrm {cyc}}(0) = S_{\mu }(0)$
and
$S_{\mathrm {cyc}}(0) = S_{\mu }(0)$
and
![]() $S_{\mathrm {cyc}}(p)^{p'} = S_{\mu }(p)^{p'}$
, where
$S_{\mathrm {cyc}}(p)^{p'} = S_{\mu }(p)^{p'}$
, where
![]() $(-)^{p'}$
denotes the subset of prime-to-p elements.
$(-)^{p'}$
denotes the subset of prime-to-p elements.
Remark 8.1. Keum [Reference Katsura and TakedaKe, Main Theorem] proved the following results on
![]() $S_{\mathrm {cyc}}(p)$
. (This set is denoted by
$S_{\mathrm {cyc}}(p)$
. (This set is denoted by
![]() $\mathrm {Ord}_p$
in his paper.) The sets
$\mathrm {Ord}_p$
in his paper.) The sets
![]() $S_{\mathrm {cyc}}(p)$
for
$S_{\mathrm {cyc}}(p)$
for
![]() $p \neq 2,3$
are given by
$p \neq 2,3$
are given by
 $$ \begin{align*} &\qquad\qquad\qquad\qquad\qquad \ S_{\mathrm{cyc}}(0) = \{n : \phi(n) \leq 20\} \\ &= \{1, \dots, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 36, 38, 40, 42, 44, 48, 50, 54, 60, 66\}, \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad\qquad\qquad \ S_{\mathrm{cyc}}(0) = \{n : \phi(n) \leq 20\} \\ &= \{1, \dots, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 36, 38, 40, 42, 44, 48, 50, 54, 60, 66\}, \end{align*} $$
and
 $$\begin{align*}S_{\mathrm{cyc}}(p) = \begin{cases} S_{\mathrm{cyc}}(0), & \text{if } p = 7 \text{ or } p \geq 23, \\ S_{\mathrm{cyc}}(0) \setminus \{p,2p\}, & \text{if } p = 13,17,19, \\ S_{\mathrm{cyc}}(0) \setminus \{44\}, & \text{if } p = 11, \\ S_{\mathrm{cyc}}(0) \setminus \{25,50,60\}, & \text{if } p = 5. \\ \end{cases} \end{align*}$$
$$\begin{align*}S_{\mathrm{cyc}}(p) = \begin{cases} S_{\mathrm{cyc}}(0), & \text{if } p = 7 \text{ or } p \geq 23, \\ S_{\mathrm{cyc}}(0) \setminus \{p,2p\}, & \text{if } p = 13,17,19, \\ S_{\mathrm{cyc}}(0) \setminus \{44\}, & \text{if } p = 11, \\ S_{\mathrm{cyc}}(0) \setminus \{25,50,60\}, & \text{if } p = 5. \\ \end{cases} \end{align*}$$
Moreover,
![]() $S_{\mathrm {cyc}}(p)^{p'} = S_{\mathrm {cyc}}(0)^{p'}$
for all
$S_{\mathrm {cyc}}(p)^{p'} = S_{\mathrm {cyc}}(0)^{p'}$
for all
![]() $p \geq 2$
. (The sets
$p \geq 2$
. (The sets
![]() $S_{\mathrm {cyc}}(2)$
and
$S_{\mathrm {cyc}}(2)$
and
![]() $S_{\mathrm {cyc}}(3)$
are not determined.)
$S_{\mathrm {cyc}}(3)$
are not determined.)
In this section, we determine the set
![]() $S_{\mu }(p)$
for all p.
$S_{\mu }(p)$
for all p.
Theorem 8.2. We have
 $$\begin{align*}S_{\mu}(p) = \begin{cases} S_{\mathrm{cyc}}(0), & \text{if } p \neq 2,3,5,11, \\ S_{\mathrm{cyc}}(0) \setminus \{33,66\}, & \text{if } p = 11, \\ S_{\mathrm{cyc}}(0) \setminus \{25,40,50\}, & \text{if } p = 5, \\ S_{\mathrm{cyc}}(0) \setminus \{27,33,48,54,66\}, & \text{if } p = 3, \\ S_{\mathrm{cyc}}(0) \setminus \{34,40,44,48,50,54,66\}, & \text{if } p = 2. \end{cases} \end{align*}$$
$$\begin{align*}S_{\mu}(p) = \begin{cases} S_{\mathrm{cyc}}(0), & \text{if } p \neq 2,3,5,11, \\ S_{\mathrm{cyc}}(0) \setminus \{33,66\}, & \text{if } p = 11, \\ S_{\mathrm{cyc}}(0) \setminus \{25,40,50\}, & \text{if } p = 5, \\ S_{\mathrm{cyc}}(0) \setminus \{27,33,48,54,66\}, & \text{if } p = 3, \\ S_{\mathrm{cyc}}(0) \setminus \{34,40,44,48,50,54,66\}, & \text{if } p = 2. \end{cases} \end{align*}$$
In particular, there exists an RDP K3 surface equipped with a nontrivial
![]() $\mu _p$
-action in characteristic p if and only if
$\mu _p$
-action in characteristic p if and only if
![]() $p \leq 19$
.
$p \leq 19$
.
We need some preparations. The height h of a K3 surface X in characteristic
![]() $p> 0$
, whose definition we do not recall here, is either
$p> 0$
, whose definition we do not recall here, is either
![]() $\infty $
or an integer in
$\infty $
or an integer in
![]() $\{1, \dots , 10\}$
, and X is called supersingular or of finite height, respectively. If
$\{1, \dots , 10\}$
, and X is called supersingular or of finite height, respectively. If
![]() $h < \infty $
, then the inequality
$h < \infty $
, then the inequality
![]() $\rho \leq 22 - 2h$
holds (Lemma 8.3(2)), where
$\rho \leq 22 - 2h$
holds (Lemma 8.3(2)), where
![]() $\rho = \operatorname {\mathrm {rank}} \operatorname {\mathrm {Pic}}(X)$
is the Picard number. This implies that if
$\rho = \operatorname {\mathrm {rank}} \operatorname {\mathrm {Pic}}(X)$
is the Picard number. This implies that if
![]() $\rho \geq 21$
, then X is supersingular.
$\rho \geq 21$
, then X is supersingular.
In fact, the Tate conjecture for K3 surfaces, now a theorem, states conversely that if X is supersingular, then
![]() $\rho = 22$
(see Lemma 8.3(4) for references). In this case, the
$\rho = 22$
(see Lemma 8.3(4) for references). In this case, the
![]() $\mathbb Z_p$
-lattice
$\mathbb Z_p$
-lattice
![]() $H_{\mathrm {crys}}^2(X/W(k))^{F = p}$
is isomorphic to
$H_{\mathrm {crys}}^2(X/W(k))^{F = p}$
is isomorphic to
![]() $\operatorname {\mathrm {Pic}}(X) \otimes \mathbb Z_p$
[Reference OguisoO2, Cor. 1.6], and the discriminant group of
$\operatorname {\mathrm {Pic}}(X) \otimes \mathbb Z_p$
[Reference OguisoO2, Cor. 1.6], and the discriminant group of
![]() $H_{\mathrm {crys}}^2(X/W(k))^{F = p}$
(isomorphic to the discriminant group of
$H_{\mathrm {crys}}^2(X/W(k))^{F = p}$
(isomorphic to the discriminant group of
![]() $\operatorname {\mathrm {Pic}}(X)$
) is of the form
$\operatorname {\mathrm {Pic}}(X)$
) is of the form
![]() $(\mathbb Z/p\mathbb Z)^{2\sigma _0}$
for an integer
$(\mathbb Z/p\mathbb Z)^{2\sigma _0}$
for an integer
![]() $\sigma _0 \in \{1, \dots , 10\}$
. This
$\sigma _0 \in \{1, \dots , 10\}$
. This
![]() $\sigma _0$
is called the Artin invariant of X. Here, the discriminant group of a nondegenerate lattice (resp. nondegenerate
$\sigma _0$
is called the Artin invariant of X. Here, the discriminant group of a nondegenerate lattice (resp. nondegenerate
![]() $\mathbb Z_p$
-lattice) L is defined to be the finite group
$\mathbb Z_p$
-lattice) L is defined to be the finite group
![]() $L^*/L$
, where
$L^*/L$
, where
![]() $L^* = \operatorname {\mathrm {Hom}}_{\mathbb Z}(L, \mathbb Z)$
(resp.
$L^* = \operatorname {\mathrm {Hom}}_{\mathbb Z}(L, \mathbb Z)$
(resp.
![]() $L^* = \operatorname {\mathrm {Hom}}_{\mathbb Z_p}(L, \mathbb Z_p)$
) is the dual of L.
$L^* = \operatorname {\mathrm {Hom}}_{\mathbb Z_p}(L, \mathbb Z_p)$
) is the dual of L.
We define the crystalline transcendental lattice
![]() $T(X) = T_{\mathrm {crys}}(X) \subset H_{\mathrm {crys}}^2(X/W(k))$
to be the orthogonal complement of the image of
$T(X) = T_{\mathrm {crys}}(X) \subset H_{\mathrm {crys}}^2(X/W(k))$
to be the orthogonal complement of the image of
![]() $\operatorname {\mathrm {Pic}}(X) \otimes W(k)$
, where
$\operatorname {\mathrm {Pic}}(X) \otimes W(k)$
, where
![]() $W(k)$
is the ring of Witt vectors over k. We have
$W(k)$
is the ring of Witt vectors over k. We have
![]() $\rho + \operatorname {\mathrm {rank}} T(X) = 22$
.
$\rho + \operatorname {\mathrm {rank}} T(X) = 22$
.
We collect some facts.
Lemma 8.3. Let X be a K3 surface in characteristic
![]() $p> 0$
.
$p> 0$
.
-
1.
 $\operatorname {\mathrm {Aut}}(X)$
acts on
$\operatorname {\mathrm {Aut}}(X)$
acts on
 $H_{\mathrm {crys}}^2(X/W(k))$
and
$H_{\mathrm {crys}}^2(X/W(k))$
and
 $H_{\mathrm {\acute et}}^2(X, \mathbb Z_l)$
(for any prime
$H_{\mathrm {\acute et}}^2(X, \mathbb Z_l)$
(for any prime
 $l \neq p$
) faithfully, and the characteristic polynomial of any element is independent of the cohomology (and l) and has coefficients in
$l \neq p$
) faithfully, and the characteristic polynomial of any element is independent of the cohomology (and l) and has coefficients in
 $\mathbb Q$
.
$\mathbb Q$
. -
2. If X is of finite height h, then
 $\rho \leq 22 - 2 h$
.
$\rho \leq 22 - 2 h$
. -
3. Let
 $g \in \operatorname {\mathrm {Aut}}(X)$
and suppose it acts on
$g \in \operatorname {\mathrm {Aut}}(X)$
and suppose it acts on
 $H^0(X, \Omega ^2)$
by a primitive Nth root of
$H^0(X, \Omega ^2)$
by a primitive Nth root of
 $1$
. If X is of finite height and
$1$
. If X is of finite height and
 $p \geq 3$
, then the characteristic polynomial of
$p \geq 3$
, then the characteristic polynomial of
 $g^*$
on
$g^*$
on
 $T_{\mathrm {crys}}(X)$
is the product of cyclotomic polynomials
$T_{\mathrm {crys}}(X)$
is the product of cyclotomic polynomials
 $\Phi _{N p^{e_i}}$
with nonnegative integers
$\Phi _{N p^{e_i}}$
with nonnegative integers
 $e_i$
. In particular,
$e_i$
. In particular,
 $\phi (N) \mid \operatorname {\mathrm {rank}} T_{\mathrm {crys}}(X)$
, in particular
$\phi (N) \mid \operatorname {\mathrm {rank}} T_{\mathrm {crys}}(X)$
, in particular
 $\operatorname {\mathrm {rank}} T_{\mathrm {crys}}(X) \geq \phi (N)$
.
$\operatorname {\mathrm {rank}} T_{\mathrm {crys}}(X) \geq \phi (N)$
. -
4. If X is supersingular, then
 $\rho = 22$
.
$\rho = 22$
. -
5. Let
 $g \in \operatorname {\mathrm {Aut}}(X)$
and define N as in (3). If X is supersingular of Artin invariant
$g \in \operatorname {\mathrm {Aut}}(X)$
and define N as in (3). If X is supersingular of Artin invariant
 $\sigma _0$
, then
$\sigma _0$
, then
 $N \mid (p^{\sigma _0} + 1)$
.
$N \mid (p^{\sigma _0} + 1)$
.
An immediate consequence of (5) is that, letting
![]() $g \in \operatorname {\mathrm {Aut}}(X)$
and N be as in (3), if there exists no integer
$g \in \operatorname {\mathrm {Aut}}(X)$
and N be as in (3), if there exists no integer
![]() $\sigma _0$
with
$\sigma _0$
with
![]() $N \mid (p^{\sigma _0} + 1)$
, then X is not supersingular. This applies to, for example,
$N \mid (p^{\sigma _0} + 1)$
, then X is not supersingular. This applies to, for example,
![]() $(p,N) = (3,8), (5,4)$
.
$(p,N) = (3,8), (5,4)$
.
Proof. (1) [Reference Katsura and TakedaKe, Th. 1.4].
(2) [Reference Gille and PoloI, Prop. II.5.12].
(3) See [Reference MatsumotoMat2, Lem. 2.4(3)], which deduces the assertion from [Reference IllusieJ, Th. 3.2].
(4) This assertion, the Tate conjecture for supersingular K3 surfaces, is proved by Madapusi Pera [Reference KondōMad, Th. 1] for characteristic
![]() $\geq 3$
and by Kim and Madapusi Pera [Reference KeumKMP, Th. A.1] for characteristic
$\geq 3$
and by Kim and Madapusi Pera [Reference KeumKMP, Th. A.1] for characteristic
![]() $2$
.
$2$
.
The assertion under the assumption that X admits an elliptic fibration, which is true, for example, if
![]() $\rho \geq 5$
(which is always the case when we use this assertion in this paper), was proved much earlier by Artin [Reference ArtinA1, Th. 1.7].
$\rho \geq 5$
(which is always the case when we use this assertion in this paper), was proved much earlier by Artin [Reference ArtinA1, Th. 1.7].
(5) This is proved by Nygaard [Reference NygaardNy2, Th. 2.1] under the assumption
![]() $p \neq 2$
. The argument is in fact valid for
$p \neq 2$
. The argument is in fact valid for
![]() $p = 2$
(see [Reference MatsumotoMat2, Rem. 2.2]).
$p = 2$
(see [Reference MatsumotoMat2, Rem. 2.2]).
Proof of Theorem 8.2
Let
![]() $S_{\mu }'(p)$
be the set on the right-hand side of the statement. If n is a positive integer not divisible by p, then
$S_{\mu }'(p)$
be the set on the right-hand side of the statement. If n is a positive integer not divisible by p, then
![]() $\mu _n$
-action is equivalent to the action a cyclic group of order n and, as noted in Remark 8.1, Keum [Reference Katsura and TakedaKe, Main Theorem] proved that n is the order of some automorphism of a K3 surface in characteristic p if and only if
$\mu _n$
-action is equivalent to the action a cyclic group of order n and, as noted in Remark 8.1, Keum [Reference Katsura and TakedaKe, Main Theorem] proved that n is the order of some automorphism of a K3 surface in characteristic p if and only if
![]() $n \in S_{\mu }'(p)$
(equivalently
$n \in S_{\mu }'(p)$
(equivalently
![]() $n \in S_{\mu }(0)$
).
$n \in S_{\mu }(0)$
).
If
![]() $n \in S_{\mu }'(p)$
and
$n \in S_{\mu }'(p)$
and
![]() $p \mid n$
, then the examples given in Example 9.6 show that
$p \mid n$
, then the examples given in Example 9.6 show that
![]() $n \in S_{\mu }(p)$
.
$n \in S_{\mu }(p)$
.
Now, take
![]() $n \in S_{\mu }(p)$
with
$n \in S_{\mu }(p)$
with
![]() $p \mid n$
, and we will show
$p \mid n$
, and we will show
![]() $n \in S_{\mu }'(p)$
. Write
$n \in S_{\mu }'(p)$
. Write
![]() $n = p^e r$
with
$n = p^e r$
with
![]() $p \nmid r$
. Since a smooth K3 surface never admits a
$p \nmid r$
. Since a smooth K3 surface never admits a
![]() $\mu _p$
-action, an example X must have an RDP w. Since
$\mu _p$
-action, an example X must have an RDP w. Since
![]() $\mu _{p^e}$
-fixed RDPs can be blown up, we may assume w is not
$\mu _{p^e}$
-fixed RDPs can be blown up, we may assume w is not
![]() $\mu _{p^e}$
-fixed. Note that such RDPs are classified in Proposition 4.12. We show in each case that n belongs to
$\mu _{p^e}$
-fixed. Note that such RDPs are classified in Proposition 4.12. We show in each case that n belongs to
![]() $S_{\mu }'(p)$
.
$S_{\mu }'(p)$
.
Suppose w is
![]() $D_m$
or
$D_m$
or
![]() $E_m$
. Let
$E_m$
. Let
![]() $\mu _{p^f s} = \operatorname {\mathrm {Stab}}(w) \subset \mu _{p^e r}$
(with
$\mu _{p^f s} = \operatorname {\mathrm {Stab}}(w) \subset \mu _{p^e r}$
(with
![]() $p \nmid s$
). Then the pair
$p \nmid s$
). Then the pair
![]() $(w, p^e s)$
appears in Table 5 and we have
$(w, p^e s)$
appears in Table 5 and we have
![]() $(r/s)m < 22$
. Then we observe that
$(r/s)m < 22$
. Then we observe that
![]() $n \in S_{\mu }'(p)$
except in the following cases:
$n \in S_{\mu }'(p)$
except in the following cases:
![]() $(p,n,s,(r/s)w) = (2,54,9,3E_7^0), (2,40,5,D_{21}^0), (2,34,17,D_{18}^0), (2,34,17,D_{19}^0)$
. These exceptional cases do not occur, since it follows that
$(p,n,s,(r/s)w) = (2,54,9,3E_7^0), (2,40,5,D_{21}^0), (2,34,17,D_{18}^0), (2,34,17,D_{19}^0)$
. These exceptional cases do not occur, since it follows that
![]() $\mu _s$
acts trivially on the classes of every (
$\mu _s$
acts trivially on the classes of every (
![]() $21, 21, 18, 19$
) exceptional curves, which gives a too large invariant subspace of
$21, 21, 18, 19$
) exceptional curves, which gives a too large invariant subspace of
![]() $H_{\mathrm {\acute et}}^2(\tilde {X}, \mathbb Q_l)$
for an order s automorphism (which must act on
$H_{\mathrm {\acute et}}^2(\tilde {X}, \mathbb Q_l)$
for an order s automorphism (which must act on
![]() $H_{\mathrm {\acute et}}^2$
faithfully with a characteristic polynomial with coefficients in
$H_{\mathrm {\acute et}}^2$
faithfully with a characteristic polynomial with coefficients in
![]() $\mathbb Q$
by Lemma 8.3(1)).
$\mathbb Q$
by Lemma 8.3(1)).
Suppose w is
![]() $A_{m'-1}$
. Let
$A_{m'-1}$
. Let
![]() $\mu _{p^f s} = \operatorname {\mathrm {Stab}}(w) \subset \mu _{p^e r}$
(with
$\mu _{p^f s} = \operatorname {\mathrm {Stab}}(w) \subset \mu _{p^e r}$
(with
![]() $p \nmid s$
). We have
$p \nmid s$
). We have
![]() $0 \leq f < e$
. It follows from Proposition 4.12 that
$0 \leq f < e$
. It follows from Proposition 4.12 that
![]() $p^{e-f} \mid m'$
, so write
$p^{e-f} \mid m'$
, so write
![]() $m' = p^{e-f} m$
with
$m' = p^{e-f} m$
with
![]() $m \geq 1$
, and that
$m \geq 1$
, and that
![]() $\mu _{p^f t}$
acts on w symplectically where either
$\mu _{p^f t}$
acts on w symplectically where either
![]() $s = t$
or
$s = t$
or
![]() $(s,t) = (2,1)$
. Then
$(s,t) = (2,1)$
. Then
![]() $X/\mu _{p^f t}$
has
$X/\mu _{p^f t}$
has
![]() $(r/s) A_{p^f t m' - 1}$
. We have
$(r/s) A_{p^f t m' - 1}$
. We have
![]() $22> (r/s) (p^f t m' - 1) = (r/s)(p^e t m - 1) \geq r (t/s) m (p^e - 1)$
. If
$22> (r/s) (p^f t m' - 1) = (r/s)(p^e t m - 1) \geq r (t/s) m (p^e - 1)$
. If
![]() $s = t$
, then this implies
$s = t$
, then this implies
![]() $(p^e - 1)r \leq (p^e - 1)rm < 22$
, and if
$(p^e - 1)r \leq (p^e - 1)rm < 22$
, and if
![]() $(s,t) = (2,1)$
, then this implies (
$(s,t) = (2,1)$
, then this implies (
![]() $p \neq 2$
and)
$p \neq 2$
and)
![]() $2 \mid r$
and
$2 \mid r$
and
![]() $(p^e - 1)r \leq (p^e - 1)rm < 44$
. We observe that this condition implies either
$(p^e - 1)r \leq (p^e - 1)rm < 44$
. We observe that this condition implies either
![]() $n \in S_{\mu }'(p)$
or
$n \in S_{\mu }'(p)$
or
![]() $(p,n) = (5,40), (3,48), (2,34)$
. It remains to show that each of the latter three cases is impossible.
$(p,n) = (5,40), (3,48), (2,34)$
. It remains to show that each of the latter three cases is impossible.
If
![]() $(p,n) = (3,48)$
, then
$(p,n) = (3,48)$
, then
![]() $(m,s,t) = (1,2,1)$
. Since
$(m,s,t) = (1,2,1)$
. Since
![]() $\mu _s$
does not act symplectically, the generator of
$\mu _s$
does not act symplectically, the generator of
![]() $\mu _{16}$
acts on
$\mu _{16}$
acts on
![]() $H^0(\tilde {X}, \Omega ^2)$
by a primitive
$H^0(\tilde {X}, \Omega ^2)$
by a primitive
![]() $16$
th root of unity. If
$16$
th root of unity. If
![]() $\tilde {X}$
is of finite height, then by Lemma 8.3(3), we have
$\tilde {X}$
is of finite height, then by Lemma 8.3(3), we have
![]() $\operatorname {\mathrm {rank}} T(\tilde {X}) \geq \phi (16) = 8$
and we have
$\operatorname {\mathrm {rank}} T(\tilde {X}) \geq \phi (16) = 8$
and we have
![]() $\rho (\tilde {X})> 8 \cdot 2 = 16$
(from
$\rho (\tilde {X})> 8 \cdot 2 = 16$
(from
![]() $8A_2$
), contradicting
$8A_2$
), contradicting
![]() $\rho + \operatorname {\mathrm {rank}} T(\tilde {X}) = 22$
. By the remark after Lemma 8.3,
$\rho + \operatorname {\mathrm {rank}} T(\tilde {X}) = 22$
. By the remark after Lemma 8.3,
![]() $\tilde {X}$
cannot be supersingular.
$\tilde {X}$
cannot be supersingular.
If
![]() $(p,n) = (2,34)$
, then
$(p,n) = (2,34)$
, then
![]() $(m,s,t) = (1,1,1)$
. Let
$(m,s,t) = (1,1,1)$
. Let
![]() $e_i$
(
$e_i$
(
![]() $i \in \mathbb Z/17\mathbb Z$
) be the exceptional curves above the
$i \in \mathbb Z/17\mathbb Z$
) be the exceptional curves above the
![]() $\mu _{17}$
-orbit of w, numbered in a way that a generator
$\mu _{17}$
-orbit of w, numbered in a way that a generator
![]() $g \in \mu _{17}$
acts by
$g \in \mu _{17}$
acts by
![]() $g(e_i) = e_{i+1}$
. Let
$g(e_i) = e_{i+1}$
. Let
![]() $L \subset \operatorname {\mathrm {Pic}}(\tilde {X})$
be the sublattice generated by
$L \subset \operatorname {\mathrm {Pic}}(\tilde {X})$
be the sublattice generated by
![]() $e_i$
’s, and
$e_i$
’s, and
![]() $L' = \operatorname {\mathrm {Pic}}(\tilde {X}) \cap \mathbb Q L$
its primitive closure.
$L' = \operatorname {\mathrm {Pic}}(\tilde {X}) \cap \mathbb Q L$
its primitive closure.
First, suppose
![]() $\tilde {X}$
is of finite height. Then, by Corollary 6.4 the
$\tilde {X}$
is of finite height. Then, by Corollary 6.4 the
![]() $\mu _2$
-action is symplectic. We may assume that X is maximal, in which case the number of RDPs on X (which are all of type
$\mu _2$
-action is symplectic. We may assume that X is maximal, in which case the number of RDPs on X (which are all of type
![]() $A_1$
) is
$A_1$
) is
![]() $8$
by Proposition 6.8, which is not compatible with the
$8$
by Proposition 6.8, which is not compatible with the
![]() $\mu _{17}$
-action.
$\mu _{17}$
-action.
Next, suppose
![]() $\tilde {X}$
is supersingular. By Lemma 8.3(5), the only possible Artin invariant is
$\tilde {X}$
is supersingular. By Lemma 8.3(5), the only possible Artin invariant is
![]() $\sigma _0 = 4$
. By Lemma 8.4 (applied to
$\sigma _0 = 4$
. By Lemma 8.4 (applied to
![]() $L_1 = L'$
,
$L_1 = L'$
,
![]() $L_2 = L^{\prime \perp }$
,
$L_2 = L^{\prime \perp }$
,
![]() $M = \operatorname {\mathrm {Pic}}(\tilde {X})$
,
$M = \operatorname {\mathrm {Pic}}(\tilde {X})$
,
![]() $\bar {M} = \operatorname {\mathrm {Pic}}(\tilde {X})^*$
, and
$\bar {M} = \operatorname {\mathrm {Pic}}(\tilde {X})^*$
, and
![]() $\bar {L}_i = L_i^*$
), we have
$\bar {L}_i = L_i^*$
), we have
 $$ \begin{align*} \operatorname{\mathrm{rank}} (\operatorname{\mathrm{disc}}(L')) &\leq \dim_{\mathbb F_2}(\operatorname{\mathrm{disc}}(\operatorname{\mathrm{Pic}}(\tilde{X}))) + \operatorname{\mathrm{rank}}(\operatorname{\mathrm{disc}}(L^{\prime \perp})) \\ &\leq \dim_{\mathbb F_2}(\operatorname{\mathrm{disc}}(\operatorname{\mathrm{Pic}}(\tilde{X}))) + \operatorname{\mathrm{rank}}(L^{\prime \perp}) \\ &= 2 \sigma_0 + (22 - \operatorname{\mathrm{rank}} L') = 13. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{rank}} (\operatorname{\mathrm{disc}}(L')) &\leq \dim_{\mathbb F_2}(\operatorname{\mathrm{disc}}(\operatorname{\mathrm{Pic}}(\tilde{X}))) + \operatorname{\mathrm{rank}}(\operatorname{\mathrm{disc}}(L^{\prime \perp})) \\ &\leq \dim_{\mathbb F_2}(\operatorname{\mathrm{disc}}(\operatorname{\mathrm{Pic}}(\tilde{X}))) + \operatorname{\mathrm{rank}}(L^{\prime \perp}) \\ &= 2 \sigma_0 + (22 - \operatorname{\mathrm{rank}} L') = 13. \end{align*} $$
Since
![]() $\operatorname {\mathrm {disc}}(L) \cong (\mathbb Z/2\mathbb Z)^{\oplus 17}$
has rank
$\operatorname {\mathrm {disc}}(L) \cong (\mathbb Z/2\mathbb Z)^{\oplus 17}$
has rank
![]() $17$
, we obtain
$17$
, we obtain
![]() $L \subsetneq L'$
. Let
$L \subsetneq L'$
. Let
![]() $V \subset 2^{\mathbb Z/17\mathbb Z}$
be the set of subsets
$V \subset 2^{\mathbb Z/17\mathbb Z}$
be the set of subsets
![]() $S \subset \mathbb Z/17\mathbb Z$
such that
$S \subset \mathbb Z/17\mathbb Z$
such that
![]() $(1/2) \sum _{i \in S} e_i \in L'$
. Then V is naturally a g-stable
$(1/2) \sum _{i \in S} e_i \in L'$
. Then V is naturally a g-stable
![]() $\mathbb F_2$
-vector space, and is nonzero, and we can identify it with a nonzero
$\mathbb F_2$
-vector space, and is nonzero, and we can identify it with a nonzero
![]() $\mathbb F_2[x]$
-submodule V of
$\mathbb F_2[x]$
-submodule V of
![]() $\mathbb F_2[x] / (x^{17} - 1)$
. Clearly,
$\mathbb F_2[x] / (x^{17} - 1)$
. Clearly,
![]() $V = Q(x) \cdot \mathbb F_2[x] / (x^{17} - 1)$
for some
$V = Q(x) \cdot \mathbb F_2[x] / (x^{17} - 1)$
for some
![]() $Q(x) \in \mathbb F_2[x]$
dividing
$Q(x) \in \mathbb F_2[x]$
dividing
![]() $x^{17} - 1$
. Using the factorization
$x^{17} - 1$
. Using the factorization
![]() $ x^{17} - 1 = (x - 1) F_{17,1}(x) F_{17,2}(x) $
in
$ x^{17} - 1 = (x - 1) F_{17,1}(x) F_{17,2}(x) $
in
![]() $\mathbb F_2[x]$
, where
$\mathbb F_2[x]$
, where
 $$ \begin{align*} F_{17,1}(x) &= x^8 + x^7 + x^6 + x^4 + x^2 + x + 1 \quad \text{and} \\ F_{17,2}(x) &= x^8 + x^5 + x^4 + x^3 + 1 \end{align*} $$
$$ \begin{align*} F_{17,1}(x) &= x^8 + x^7 + x^6 + x^4 + x^2 + x + 1 \quad \text{and} \\ F_{17,2}(x) &= x^8 + x^5 + x^4 + x^3 + 1 \end{align*} $$
are irreducible, it follows that V contains at least one of
 $$ \begin{align*} (x^{17} - 1) / (x - 1) &= x^{16} + \dots + 1, \\ (x^{17} - 1) / F_{17,1}(x) &= x^9 + x^8 + x^6 + x^3 + x + 1, \quad \text{or} \\ (x^{17} - 1) / F_{17,2}(x) &= x^9 + x^6 + x^5 + x^4 + x^3 + 1. \end{align*} $$
$$ \begin{align*} (x^{17} - 1) / (x - 1) &= x^{16} + \dots + 1, \\ (x^{17} - 1) / F_{17,1}(x) &= x^9 + x^8 + x^6 + x^3 + x + 1, \quad \text{or} \\ (x^{17} - 1) / F_{17,2}(x) &= x^9 + x^6 + x^5 + x^4 + x^3 + 1. \end{align*} $$
Hence, there exists a set
![]() $S \in V$
with
$S \in V$
with
![]() $\# S = 17$
or
$\# S = 17$
or
![]() $\# S = 6$
. But then,
$\# S = 6$
. But then,
![]() $((1/2) \sum _{i \in S} e_i)^2 = (1/2)^2 \cdot \# S \cdot (-2) \not \in 2\mathbb Z$
, contradiction.
$((1/2) \sum _{i \in S} e_i)^2 = (1/2)^2 \cdot \# S \cdot (-2) \not \in 2\mathbb Z$
, contradiction.
If
![]() $(p,n) = (5,40)$
, then
$(p,n) = (5,40)$
, then
![]() $(m,s,t) = (1,2,1)$
and there are four non-
$(m,s,t) = (1,2,1)$
and there are four non-
![]() $\mu _5$
-fixed
$\mu _5$
-fixed
![]() $A_4$
on which g acts transitively, where g is a fixed generator of
$A_4$
on which g acts transitively, where g is a fixed generator of
![]() $\mu _8 \subset \mu _{40}$
, and
$\mu _8 \subset \mu _{40}$
, and
![]() $g^4$
is non-symplectic. Moreover,
$g^4$
is non-symplectic. Moreover,
![]() $\operatorname {\mathrm {Fix}}(g^4)$
is one-dimensional, passing through the four points of type
$\operatorname {\mathrm {Fix}}(g^4)$
is one-dimensional, passing through the four points of type
![]() $A_4$
.
$A_4$
.
By the remark after Lemma 8.3,
![]() $\tilde {X}$
cannot be supersingular. This implies that the
$\tilde {X}$
cannot be supersingular. This implies that the
![]() $\mu _5$
-action is symplectic (Corollary 6.4) and hence the quotient
$\mu _5$
-action is symplectic (Corollary 6.4) and hence the quotient
![]() $Y = X/\mu _5$
is an RDP K3 surface.
$Y = X/\mu _5$
is an RDP K3 surface.
We will show in a subsequent paper [Reference MatsumotoMat3, Prop. 2.15(4)] that the
![]() $\mu _p$
-action induces a canonical nonzero element
$\mu _p$
-action induces a canonical nonzero element
![]() $v \in H^0(Y^{\mathrm {sm}}, \Omega ^2) \otimes \operatorname {\mathrm {Der}}(Y)$
, which we can write
$v \in H^0(Y^{\mathrm {sm}}, \Omega ^2) \otimes \operatorname {\mathrm {Der}}(Y)$
, which we can write
![]() $v = \omega _Y \otimes D_Y$
(uniquely up to
$v = \omega _Y \otimes D_Y$
(uniquely up to
![]() $k^*$
), such that
$k^*$
), such that
![]() $D_Y$
is p-closed and satisfies
$D_Y$
is p-closed and satisfies
![]() $Y^{D_Y} = {X}^{(p)}$
. It is characterized by
$Y^{D_Y} = {X}^{(p)}$
. It is characterized by
![]() $D(f)^p D_Y(h) \omega _Y = d(f^p) \wedge dh$
for local sections f of
$D(f)^p D_Y(h) \omega _Y = d(f^p) \wedge dh$
for local sections f of
![]() $\mathcal {O}_X$
and h of
$\mathcal {O}_X$
and h of
![]() $\mathcal {O}_Y$
. Since the
$\mathcal {O}_Y$
. Since the
![]() $\mu _5$
-action in our case is g-invariant, it follows that
$\mu _5$
-action in our case is g-invariant, it follows that
![]() $v = \omega _Y \otimes D_Y$
is g-invariant.
$v = \omega _Y \otimes D_Y$
is g-invariant.
Fix a decomposition
![]() $v = \omega _Y \otimes D_Y$
. We have
$v = \omega _Y \otimes D_Y$
. We have
![]() $D_Y^p = \phi D_Y$
for some meromorphic function
$D_Y^p = \phi D_Y$
for some meromorphic function
![]() $\phi $
. Since both Y and the quotient
$\phi $
. Since both Y and the quotient
![]() $Y^{D_Y} \cong {X}^{(p)}$
are RDP K3 surfaces, it follows from the Rudakov–Shafarevich formula [Reference OgusRS, Cor. 1 to Prop. 3] that
$Y^{D_Y} \cong {X}^{(p)}$
are RDP K3 surfaces, it follows from the Rudakov–Shafarevich formula [Reference OgusRS, Cor. 1 to Prop. 3] that
![]() $D_Y$
has only isolated fixed points, and this implies that
$D_Y$
has only isolated fixed points, and this implies that
![]() $\phi $
is holomorphic, hence constant. We have
$\phi $
is holomorphic, hence constant. We have
![]() $\phi \neq 0$
, since if
$\phi \neq 0$
, since if
![]() $\phi = 0$
, then, as we will prove in a subsequent paper [Reference MatsumotoMat3, Lem. 3.6 or Th. 4.6], the
$\phi = 0$
, then, as we will prove in a subsequent paper [Reference MatsumotoMat3, Lem. 3.6 or Th. 4.6], the
![]() $\alpha _p$
-action corresponding to
$\alpha _p$
-action corresponding to
![]() $D_Y$
must have quotient singularities different from
$D_Y$
must have quotient singularities different from
![]() $A_{p-1}$
, but X has only RDPs of type
$A_{p-1}$
, but X has only RDPs of type
![]() $A_{p-1}$
. Since
$A_{p-1}$
. Since
![]() $\operatorname {\mathrm {Fix}}(D_Y)$
is isolated and
$\operatorname {\mathrm {Fix}}(D_Y)$
is isolated and
![]() $Y^{D_Y} = Y^{g^*(D_Y)}$
, we have
$Y^{D_Y} = Y^{g^*(D_Y)}$
, we have
![]() $g^*(D_Y) = \lambda D_Y$
with
$g^*(D_Y) = \lambda D_Y$
with
![]() $\lambda \in H^0(Y, \mathcal {O})^* = k^*$
, and since
$\lambda \in H^0(Y, \mathcal {O})^* = k^*$
, and since
![]() $D_Y^p = \phi D_Y$
with
$D_Y^p = \phi D_Y$
with
![]() $\phi \in k^*$
, we have
$\phi \in k^*$
, we have
![]() $\lambda ^{p-1} = 1$
, and hence
$\lambda ^{p-1} = 1$
, and hence
![]() $(g^4)^{*}(D_Y) = D_Y$
.
$(g^4)^{*}(D_Y) = D_Y$
.
On the other hand, since
![]() $\operatorname {\mathrm {Fix}}(g^4 \curvearrowright Y)$
is homeomorphic to
$\operatorname {\mathrm {Fix}}(g^4 \curvearrowright Y)$
is homeomorphic to
![]() $\operatorname {\mathrm {Fix}}(g^4 \curvearrowright X)$
and hence is one-dimensional, we have
$\operatorname {\mathrm {Fix}}(g^4 \curvearrowright X)$
and hence is one-dimensional, we have
![]() $(g^4)^{*}(\omega _Y) = - \omega _Y$
. This contradicts the g-invariance of
$(g^4)^{*}(\omega _Y) = - \omega _Y$
. This contradicts the g-invariance of
![]() $v = \omega _Y \otimes D_Y$
.
$v = \omega _Y \otimes D_Y$
.
Lemma 8.4. Let
![]() $L_1 \subset \bar {L}_1$
,
$L_1 \subset \bar {L}_1$
,
![]() $L_2 \subset \bar {L}_2$
, and
$L_2 \subset \bar {L}_2$
, and
![]() $L_1 \oplus L_2 \subset M \subset \bar {M} \subset \bar {L}_1 \oplus \bar {L}_2$
be sequences of abelian groups, where the bars have no specific meaning. Assume that the projection
$L_1 \oplus L_2 \subset M \subset \bar {M} \subset \bar {L}_1 \oplus \bar {L}_2$
be sequences of abelian groups, where the bars have no specific meaning. Assume that the projection
![]() $\bar {M} \to \bar {L}_1$
are surjective and that
$\bar {M} \to \bar {L}_1$
are surjective and that
![]() $M \cap (\bar {L}_1 \oplus 0) = L_1 \oplus 0$
. Then we have
$M \cap (\bar {L}_1 \oplus 0) = L_1 \oplus 0$
. Then we have
![]() $\operatorname {\mathrm {rank}}(\bar {L}_1 / L_1) \leq \operatorname {\mathrm {rank}}(\bar {M}/M) + \operatorname {\mathrm {rank}}(\bar {L}_2 / L_2)$
, where the rank of an abelian group is the minimum number of generators.
$\operatorname {\mathrm {rank}}(\bar {L}_1 / L_1) \leq \operatorname {\mathrm {rank}}(\bar {M}/M) + \operatorname {\mathrm {rank}}(\bar {L}_2 / L_2)$
, where the rank of an abelian group is the minimum number of generators.
Proof. We may assume
![]() $L_i = 0$
. The assumption then implies that
$L_i = 0$
. The assumption then implies that
![]() $M \to \bar {L}_2$
is injective. Since the rank behaves subadditively with respect to subgroups, quotients, and extensions, we obtain
$M \to \bar {L}_2$
is injective. Since the rank behaves subadditively with respect to subgroups, quotients, and extensions, we obtain
![]() $\operatorname {\mathrm {rank}}(\bar {L}_1) \leq \operatorname {\mathrm {rank}}(\bar {M}) \leq \operatorname {\mathrm {rank}}(M) + \operatorname {\mathrm {rank}}(\bar {M}/M) \leq \operatorname {\mathrm {rank}}(\bar {L}_2) + \operatorname {\mathrm {rank}}(\bar {M}/M)$
.
$\operatorname {\mathrm {rank}}(\bar {L}_1) \leq \operatorname {\mathrm {rank}}(\bar {M}) \leq \operatorname {\mathrm {rank}}(M) + \operatorname {\mathrm {rank}}(\bar {M}/M) \leq \operatorname {\mathrm {rank}}(\bar {L}_2) + \operatorname {\mathrm {rank}}(\bar {M}/M)$
.
9 Examples
For a projective variety with projective coordinates
![]() $(x_i)$
, we use the notation
$(x_i)$
, we use the notation
![]() $\operatorname {\mathrm {wt}}(x_i) = (n_i)$
to mean that
$\operatorname {\mathrm {wt}}(x_i) = (n_i)$
to mean that
![]() $\operatorname {\mathrm {wt}}(x_j/x_i) = (n_j - n_i)$
on the affine piece
$\operatorname {\mathrm {wt}}(x_j/x_i) = (n_j - n_i)$
on the affine piece
![]() $(x_i \neq 0)$
for each i. Note that
$(x_i \neq 0)$
for each i. Note that
![]() $\operatorname {\mathrm {wt}}(x_i) = (n_i)$
is equivalent to
$\operatorname {\mathrm {wt}}(x_i) = (n_i)$
is equivalent to
![]() $\operatorname {\mathrm {wt}}(x_i) = (a + n_i)$
. We use a similar notation for subvarieties of
$\operatorname {\mathrm {wt}}(x_i) = (a + n_i)$
. We use a similar notation for subvarieties of
![]() $\mathbb P(3,1,1,1)$
.
$\mathbb P(3,1,1,1)$
.
9.1 Symplectic actions
Example 9.1 (Symplectic
 $\mu _4 \times \mu _4$
-action)
$\mu _4 \times \mu _4$
-action)
The quartic surface
![]() $X = (w^4 + x^4 + y^4 + z^4 + wxyz = 0)$
in characteristic
$X = (w^4 + x^4 + y^4 + z^4 + wxyz = 0)$
in characteristic
![]() $p = 2$
is an RDP K3 surface. It has six RDPs, all of type
$p = 2$
is an RDP K3 surface. It has six RDPs, all of type
![]() $A_3$
, at the points where two of
$A_3$
, at the points where two of
![]() $w,x,y,z$
are
$w,x,y,z$
are
![]() $0$
and the others are
$0$
and the others are
![]() $1$
. This surface admits a symplectic action of
$1$
. This surface admits a symplectic action of
![]() $G = H_1 \times H_2$
, where
$G = H_1 \times H_2$
, where
![]() $H_1 = \mu _4$
and
$H_1 = \mu _4$
and
![]() $H_2 = \mu _4$
act by
$H_2 = \mu _4$
act by
![]() $\operatorname {\mathrm {wt}}(w,x,y,z) = (0,0,1,-1)$
and
$\operatorname {\mathrm {wt}}(w,x,y,z) = (0,0,1,-1)$
and
![]() $\operatorname {\mathrm {wt}}(w,x,y,z) = (0,1,0,-1)$
, respectively.
$\operatorname {\mathrm {wt}}(w,x,y,z) = (0,1,0,-1)$
, respectively.
With respect to the action of the subgroup scheme
![]() $\mu _2 \subset H_1$
, the two RDPs at
$\mu _2 \subset H_1$
, the two RDPs at
![]() $(0,0,1,1)$
and
$(0,0,1,1)$
and
![]() $(1,1,0,0)$
are fixed and the other four RDPs are non-fixed and non-maximal. The quotient surface by this
$(1,1,0,0)$
are fixed and the other four RDPs are non-fixed and non-maximal. The quotient surface by this
![]() $\mu _2$
-action is
$\mu _2$
-action is
![]() $(W^2 + X^2 + Y^2 + Z^2 + AB = WX - A^2 = YZ - B^2 = 0)$
in
$(W^2 + X^2 + Y^2 + Z^2 + AB = WX - A^2 = YZ - B^2 = 0)$
in
![]() $\mathbb P^5$
, where
$\mathbb P^5$
, where
![]() $W = w^2, \dots , Z = z^2$
and
$W = w^2, \dots , Z = z^2$
and
![]() $A = wx, B = yz$
, with two RDPs of type
$A = wx, B = yz$
, with two RDPs of type
![]() $A_7$
at
$A_7$
at
![]() $(Y = Z = B = W+X = W+A = 0),(W = X = A = Y+Z = Y+B = 0)$
and four of type
$(Y = Z = B = W+X = W+A = 0),(W = X = A = Y+Z = Y+B = 0)$
and four of type
![]() $A_1$
at
$A_1$
at
![]() $(WX = A = YZ = B = W + X + Y + Z = 0)$
.
$(WX = A = YZ = B = W + X + Y + Z = 0)$
.
The quotient morphism by the subgroup scheme
![]() $\mu _2 \times \mu _2$
(resp. the full group G) is the relative Frobenius morphism
$\mu _2 \times \mu _2$
(resp. the full group G) is the relative Frobenius morphism
![]() $X \to X^{(2)}$
(resp.
$X \to X^{(2)}$
(resp.
![]() $X \to X^{(4)}$
).
$X \to X^{(4)}$
).
Example 9.2 (Symplectic
 $\mu _3 \times \mu _3$
-action)
$\mu _3 \times \mu _3$
-action)
The surface
![]() $X = (v^3 + w^3 + x^3 + y^3 + z^3 + vwx = v^2 - yz = 0) \subset \mathbb P^4$
in characteristic
$X = (v^3 + w^3 + x^3 + y^3 + z^3 + vwx = v^2 - yz = 0) \subset \mathbb P^4$
in characteristic
![]() $p = 3$
is an RDP K3 surface, and has
$p = 3$
is an RDP K3 surface, and has
![]() $2A_5$
at
$2A_5$
at
![]() $(1,0,0,1,1),(0,1,-1,0,0)$
and
$(1,0,0,1,1),(0,1,-1,0,0)$
and
![]() $4A_2$
at
$4A_2$
at
![]() $(0,1,0,-1,0),(0,1,0,0,-1),(0,0,1,-1,0),(0,0,1,0,-1)$
. This surface admits a symplectic action of
$(0,1,0,-1,0),(0,1,0,0,-1),(0,0,1,-1,0),(0,0,1,0,-1)$
. This surface admits a symplectic action of
![]() $G = H_1 \times H_2$
, where
$G = H_1 \times H_2$
, where
![]() $H_1 = \mu _3$
and
$H_1 = \mu _3$
and
![]() $H_2 = \mu _3$
act by
$H_2 = \mu _3$
act by
![]() $\operatorname {\mathrm {wt}}(v,w,x,y,z) = (0,1,-1,0,0)$
and
$\operatorname {\mathrm {wt}}(v,w,x,y,z) = (0,1,-1,0,0)$
and
![]() $\operatorname {\mathrm {wt}}(v,w,x,y,z) = (0,0,0,1,-1)$
, respectively. Let
$\operatorname {\mathrm {wt}}(v,w,x,y,z) = (0,0,0,1,-1)$
, respectively. Let
![]() $D_1,D_2$
be the corresponding derivations. The fixed points of
$D_1,D_2$
be the corresponding derivations. The fixed points of
![]() $D_1$
(resp.
$D_1$
(resp.
![]() $D_2$
) is the first (resp. second)
$D_2$
) is the first (resp. second)
![]() $A_5$
point. The fixed points of
$A_5$
point. The fixed points of
![]() $D_1 + D_2$
(resp.
$D_1 + D_2$
(resp.
![]() $D_1 - D_2$
), which corresponds to the diagonal (resp. anti-diagonal) subgroup of G, are the first and the fourth (resp. the second and the third)
$D_1 - D_2$
), which corresponds to the diagonal (resp. anti-diagonal) subgroup of G, are the first and the fourth (resp. the second and the third)
![]() $A_2$
points. The quotient morphism by G is the relative Frobenius morphism
$A_2$
points. The quotient morphism by G is the relative Frobenius morphism
![]() $X \to X^{(3)}$
.
$X \to X^{(3)}$
.
Example 9.3 (Symplectic
 $\mu _n$
-action (
$\mu _n$
-action (
 $n = 5,6,7,8$
))
$n = 5,6,7,8$
))
For each
![]() $n = 5,6,7,8$
, let F be a linear combination of the monomials listed in Table 8, in characteristic p, and then
$n = 5,6,7,8$
, let F be a linear combination of the monomials listed in Table 8, in characteristic p, and then
![]() $X = (F = 0) \subset \mathbb P^3$
admits a
$X = (F = 0) \subset \mathbb P^3$
admits a
![]() $\mu _n$
-action with the indicated weights. If F is a generic such polynomial, then X is an RDP K3 surface and the
$\mu _n$
-action with the indicated weights. If F is a generic such polynomial, then X is an RDP K3 surface and the
![]() $\mu _n$
-action is symplectic. The fixed locus is
$\mu _n$
-action is symplectic. The fixed locus is
![]() $X \cap \{(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1)\}$
.
$X \cap \{(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1)\}$
.
Table 8 Examples of symplectic
![]() $\mu _n$
-actions on RDP K3 surfaces.
$\mu _n$
-actions on RDP K3 surfaces.

For example, for
![]() $n = 5,6,7,8$
, respectively, the polynomials with coefficients
$n = 5,6,7,8$
, respectively, the polynomials with coefficients
![]() $(1,1,1,1,0,0,0)$
,
$(1,1,1,1,0,0,0)$
,
![]() $(1,1,1,1,1,0,0)$
,
$(1,1,1,1,1,0,0)$
,
![]() $(1,1,1,1,1)$
,
$(1,1,1,1,1)$
,
![]() $(1,1,1,1,1)$
satisfy the condition.
$(1,1,1,1,1)$
satisfy the condition.
9.2 Non-symplectic actions
Example 9.4 (Non-symplectic
 $\mu _2$
-action with Enriques quotient in characteristic
$\mu _2$
-action with Enriques quotient in characteristic
 $2$
)
$2$
)
Following [Reference Bombieri and MumfordBM1, §3], let
![]() $L_1, L_2, L_3$
be three linear polynomials in
$L_1, L_2, L_3$
be three linear polynomials in
![]() $12$
variables, and let
$12$
variables, and let
![]() $X \subset \mathbb P^5$
be the intersection of three quadrics
$X \subset \mathbb P^5$
be the intersection of three quadrics
![]() $F_1, F_2, F_3$
defined by
$F_1, F_2, F_3$
defined by
![]() $F_h = L_h(x_k^2, x_i x_j, y_k^2, y_i x_j + x_i y_j + y_i y_j)_{1 \leq k \leq 3, 1 \leq i < j \leq 3} \in k[x_1,x_2,x_3,y_1,y_2,y_3]$
. Then, for generic
$F_h = L_h(x_k^2, x_i x_j, y_k^2, y_i x_j + x_i y_j + y_i y_j)_{1 \leq k \leq 3, 1 \leq i < j \leq 3} \in k[x_1,x_2,x_3,y_1,y_2,y_3]$
. Then, for generic
![]() $L_h$
, X is an RDP K3 surface (with
$L_h$
, X is an RDP K3 surface (with
![]() $12$
RDPs of type
$12$
RDPs of type
![]() $A_1$
),
$A_1$
),
![]() $\mu _2$
acts on (
$\mu _2$
acts on (
![]() $\mathbb P^5$
and) X by
$\mathbb P^5$
and) X by
![]() $\operatorname {\mathrm {wt}}(x_i, y_i + x_i) = (0,1)$
without any fixed point on X, and the quotient
$\operatorname {\mathrm {wt}}(x_i, y_i + x_i) = (0,1)$
without any fixed point on X, and the quotient
![]() $X/\mu _2$
is an Enriques surface.
$X/\mu _2$
is an Enriques surface.
Example 9.5 (Non-symplectic
 $\mu _2$
-action with rational quotient in characteristic
$\mu _2$
-action with rational quotient in characteristic
 $2$
)
$2$
)
The quartic surface
![]() $w^2 (xy + z^2) + x^4 + y^4 + z^4 + yz(y^2 + z^2) = 0$
is an RDP K3 surface, and the
$w^2 (xy + z^2) + x^4 + y^4 + z^4 + yz(y^2 + z^2) = 0$
is an RDP K3 surface, and the
![]() $\mu _2$
-action with
$\mu _2$
-action with
![]() $\operatorname {\mathrm {wt}}(w,x,y,z) = (0,1,1,1)$
is non-symplectic. The fixed locus consists of the curve
$\operatorname {\mathrm {wt}}(w,x,y,z) = (0,1,1,1)$
is non-symplectic. The fixed locus consists of the curve
![]() $(w = 0)$
and the RDP
$(w = 0)$
and the RDP
![]() $(x = y = z = 0)$
of type
$(x = y = z = 0)$
of type
![]() $A_1$
. The image of this RDP in the quotient surface is a non-RDP singularity.
$A_1$
. The image of this RDP in the quotient surface is a non-RDP singularity.
In the following example, for two polynomials
![]() $A(t),B(t)$
with
$A(t),B(t)$
with
![]() $\deg A \leq 8$
and
$\deg A \leq 8$
and
![]() $\deg B \leq 12$
, the elliptic (or quasi-elliptic) surface defined by the equation
$\deg B \leq 12$
, the elliptic (or quasi-elliptic) surface defined by the equation
![]() $y^2 = x^3 + A(t) x + B(t)$
is an abbreviation for the projective surface that is the union of four affine surfaces
$y^2 = x^3 + A(t) x + B(t)$
is an abbreviation for the projective surface that is the union of four affine surfaces
 $$ \begin{align*} &\operatorname{\mathrm{Spec}} k[x,y,t] / (- y^2 + x^3 + A(t) x + B(t)), \\ &\operatorname{\mathrm{Spec}} k[x',y',t^{-1}] / (- y^{\prime 2} + x^{\prime 3} + t^{-8} A(t) x' + t^{-12} B(t)), \\ &\operatorname{\mathrm{Spec}} k[z,w,t] / (- z + w^3 + A(t) wz^2 + B(t) z^3), \\ &\operatorname{\mathrm{Spec}} k[z',w',t^{-1}] / (- z' + w^{\prime 3} + t^{-8} A(t) w'z^{\prime 2} + t^{-12} B(t) z^{\prime 3}), \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Spec}} k[x,y,t] / (- y^2 + x^3 + A(t) x + B(t)), \\ &\operatorname{\mathrm{Spec}} k[x',y',t^{-1}] / (- y^{\prime 2} + x^{\prime 3} + t^{-8} A(t) x' + t^{-12} B(t)), \\ &\operatorname{\mathrm{Spec}} k[z,w,t] / (- z + w^3 + A(t) wz^2 + B(t) z^3), \\ &\operatorname{\mathrm{Spec}} k[z',w',t^{-1}] / (- z' + w^{\prime 3} + t^{-8} A(t) w'z^{\prime 2} + t^{-12} B(t) z^{\prime 3}), \end{align*} $$
glued by the relations
![]() $x' = t^{-4} x$
,
$x' = t^{-4} x$
,
![]() $y' = t^{-6} y$
,
$y' = t^{-6} y$
,
![]() $z = y^{-1}$
,
$z = y^{-1}$
,
![]() $w = x y^{-1}$
,
$w = x y^{-1}$
,
![]() $z' = y^{\prime -1} = t^6 y^{-1}$
, and
$z' = y^{\prime -1} = t^6 y^{-1}$
, and
![]() $w' = x' y^{\prime -1} = t^2 x y^{-1}$
. For generic A and B, this is an RDP K3 surface.
$w' = x' y^{\prime -1} = t^2 x y^{-1}$
. For generic A and B, this is an RDP K3 surface.
Example 9.6 (Non-symplectic
 $\mu _{n}$
-actions)
$\mu _{n}$
-actions)
Table 9 proves the existence part of Theorem 8.2 for n divisible by p. The first group consists of elliptic (or quasi-elliptic) RDP K3 surfaces, the second of double sextics, and the third of quartics. Only the non-
![]() $\mu _n$
-fixed RDPs are listed, except in the example for
$\mu _n$
-fixed RDPs are listed, except in the example for
![]() $(p,n) = (2,32)$
, the
$(p,n) = (2,32)$
, the
![]() $D_{20}^0$
point is fixed and after blowing-up this point, we find a non-fixed
$D_{20}^0$
point is fixed and after blowing-up this point, we find a non-fixed
![]() $D_{18}^0$
point.
$D_{18}^0$
point.
Table 9 Examples of non-symplectic
![]() $\mu _n$
-actions on RDP K3 surfaces.
$\mu _n$
-actions on RDP K3 surfaces.

The examples are characteristic p reductions of the examples (of an automorphism of order n) in characteristic
![]() $0$
obtained, respectively, by Brandhorst [Reference BrandhorstB, Th. 5.9], Keum [Reference Katsura and TakedaKe, Exam. 3.2], Kondo [Reference Kim and Madapusi PeraKo, §§3 and 7], and Oguiso [Reference NygaardO1, Prop. 2], except that for the ones marked “?” we could not find a reference. An asterisk means that we made a coordinate change
$0$
obtained, respectively, by Brandhorst [Reference BrandhorstB, Th. 5.9], Keum [Reference Katsura and TakedaKe, Exam. 3.2], Kondo [Reference Kim and Madapusi PeraKo, §§3 and 7], and Oguiso [Reference NygaardO1, Prop. 2], except that for the ones marked “?” we could not find a reference. An asterisk means that we made a coordinate change
![]() $t \mapsto t^{-1}$
.
$t \mapsto t^{-1}$
.
9.3
 $\mu _p$
-actions on abelian surfaces
$\mu _p$
-actions on abelian surfaces
As shown in Theorem 6.3, the nontrivial
![]() $\mu _p$
-actions of abelian surfaces A, up to automorphisms of
$\mu _p$
-actions of abelian surfaces A, up to automorphisms of
![]() $\mu _p$
, are precisely the translations by subgroup schemes of
$\mu _p$
, are precisely the translations by subgroup schemes of
![]() $A[p]$
isomorphic to
$A[p]$
isomorphic to
![]() $\mu _p$
.
$\mu _p$
.
Remark 9.7. In the case of finite order automorphisms on abelian surfaces, there are examples with non-abelian quotients. Kummer surfaces in characteristic
![]() $\neq 2$
are the minimal resolution of the RDP K3 quotient (with
$\neq 2$
are the minimal resolution of the RDP K3 quotient (with
![]() $16A_1$
) by the symplectic involution
$16A_1$
) by the symplectic involution
![]() $x \mapsto -x$
on abelian surfaces (for characteristic
$x \mapsto -x$
on abelian surfaces (for characteristic
![]() $2$
, see Remark 3.6). Furthermore, certain non-symplectic (or sometimes symplectic) actions give (quasi-)hyperelliptic quotients. It seems that there are no
$2$
, see Remark 3.6). Furthermore, certain non-symplectic (or sometimes symplectic) actions give (quasi-)hyperelliptic quotients. It seems that there are no
![]() $\mu _p$
-analogue of these actions.
$\mu _p$
-analogue of these actions.
Remark 9.8. If we consider rational vector fields (i.e., possibly with poles) of multiplicative type, there are other kinds of examples. See [Reference KatsuraKT, Exam. 6.2] for a rational vector field of multiplicative type on an abelian surface (in characteristic
![]() $2$
) with a general type quotient.
$2$
) with a general type quotient.
Acknowledgments
I thank Hiroyuki Ito, Kazuhiro Ito, Shigeyuki Kondo, Christian Liedtke, Gebhard Martin, Hisanori Ohashi, Shun Ohkubo, and Tomoaki Shirato for helpful comments and discussions. I also thank the anonymous referee for a number of corrections and suggestions.