Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adolphson, Alan
and
Sperber, Steven
2011.
𝐴-hypergeometric systems that come from geometry.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 6,
p.
2033.
Lee, Roman N.
and
Pomeransky, Andrei A.
2013.
Critical points and number of master integrals.
Journal of High Energy Physics,
Vol. 2013,
Issue. 11,
Yu, Jeng-Daw
2014.
Irregular Hodge filtration on twisted de Rham cohomology.
Manuscripta Mathematica,
Vol. 144,
Issue. 1-2,
p.
99.
Grady, Daniel
and
Sati, Hisham
2018.
Twisted smooth Deligne cohomology.
Annals of Global Analysis and Geometry,
Vol. 53,
Issue. 3,
p.
445.
Fresán, Javier
Sabbah, Claude
and
Yu, Jeng-Daw
2022.
Hodge theory of Kloosterman connections.
Duke Mathematical Journal,
Vol. 171,
Issue. 8,
Sabbah, Claude
and
Yu, Jeng-Daw
2023.
Hodge properties of Airy moments.
Tunisian Journal of Mathematics,
Vol. 5,
Issue. 2,
p.
215.
Qin, Yichen
2024.
Hodge numbers of motives attached to Kloosterman and Airy moments.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Park, Jeehoon
2025.
Period integrals of smooth projective complete intersections as exponential periods.
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 1,
p.
107836.

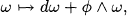 where
where 