Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-18T12:29:23.480Z Has data issue: false hasContentIssue false
  • English
  • Français

On vanishing of the twisted rational de Rham cohomology associated with hypergeometric functions

Published online by Cambridge University Press:  22 January 2016

Michitake Kita
Michitake Kita*
Affiliation:
College of Liberal Arts, Kanazawa University, Kakuma, Kanazawa 920-11, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

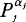Recent development in hypergeometric functions in several variables has made the importance of studying twisted rational de Rham cohomology clear to many specialists. Roughly speaking, a hypergeometric function in our sense is the integral of a product of complex powers of polynomials Pj(u1, . . . . ,un) : ∫ U du1 ∧ · · · ∧ dun, U = Π , integration being taken over some cycle. So we are led naturally to consider the twisted rational de Rham cohomology, which is a direct generalization of the usual de Rham cohomology to multivalued case.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 135 , September 1994 , pp. 55 - 85
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1994

References

[Ao] Aomoto, K., Les équations aux différences linéaires et les intégrales des fonctions multiformes, J. Fac. Sci. Univ. Tokyo, Sec. IA. 22 (1975), 271–297 and: Une correction et un complément à l’article “Les équations aux différences linéaires et les intégrales des fonctions multiformes”, ibid., 26 (1979), 519–523.Google Scholar
[AKOT] Aomoto, K., Kita, M., Orlik, P. and Terao, H., On the structure of twisted de Rham cohomology groups associated to hypergeometric integrals, preprint (1993).Google Scholar
[deR] Rham, G. de, Sur la division de formes et de courants par une formes linéaire, Comment. Math. Helv., 28 (1954), 346–352.Google Scholar
[Ka1] Kaneko, J., Monodromy group of Apell’s system (F4) , Tokyo J. Math., 4 (1981), 35–54.Google Scholar
[Ka2] Kaneko, J., Private communication, (1981).Google Scholar
[Kitl] Kita, M., On hypergeometric functions in several variables 1, New integral representations of Euler type, Japan. J. Math., 18 (1992), 25–74.Google Scholar
[Kit2] Kaneko, J., On hypergeometric functions in several variables 2, The Wronskian of the hypergeometric functions of type (n + 1, m + 1), J. Math. Soc. Japan., 45 (1993), 645–669.Google Scholar
[K-N] Kita, M. and Noumi, M., On the structure of cohomology groups attached to the integral of certain many-valued analytic functions, Japan. J. Math., 9 (1983), 113–157.Google Scholar
[M] Matsumura, H., Commutative algebra, W. A. Benjamin Co., New York (1980).Google Scholar
[MSY] Matsumoto, K., Sasaki, T. and Yoshida, M., The monodromy of the period map of a 4-parameter family of K3-surfaces and the hypergeometric function of type (3.6), Internat. J. Math., 3 (1992), 1–164.CrossRefGoogle Scholar
[O-T] Orlik, P. and Terao, H., Arrangements and Milnor fibres, preprint (1993).Google Scholar
[R-T] Rose, L. and Terao, H., A free resolution of the module of logarithmic forms of a generic arrangement, J. Algebra, 136 (1991), 376–400.Google Scholar
[SI] Saito, K., Theory of logarithmic differential forms and logarithmic vector fields, J. Fac. Sci. Univ. Tokyo, Sec. IA, 27 (1980), 265–291.Google Scholar
[S2] Saito, K., On a generalization of de Rham lemma, Ann. Inst. Fourier, Grenoble, 26 (1976), 165–170.Google Scholar
[Ya] Yamazaki, T., Private communication, (1981).Google Scholar