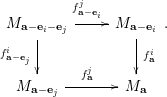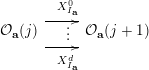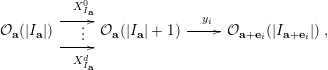1 Introduction
In their famous paper [Reference Geigle and LenzingGL], Geigle and Lenzing introduced an important class of abelian categories with a tilting object (see Definition 2.4), which have subsequently been called coherent sheaves on Geigle–Lenzing (GL) weighted projective lines. This category has played an important role in many fields, in particular representation theory of finite-dimensional algebras. It was recently generalized in [Reference Herschend, Iyama, Minamoto and OppermannHIMO] to include higher-dimensional projective spaces. A different interpretation of these categories was discovered in [Reference Chan and IngallsCI, Reference Reiten and Van den BerghRVdB] for the dimension-
![]() $1$
case and more generally in [Reference Iyama and LernerIL], where these categories are shown to be equivalent to module categories
$1$
case and more generally in [Reference Iyama and LernerIL], where these categories are shown to be equivalent to module categories
![]() $\mathsf{mod}\,A$
of a certain order
$\mathsf{mod}\,A$
of a certain order
![]() $A$
on
$A$
on
![]() $\mathbb{P}^{d}$
, which we call a GL order (see below). Both interpretations build on Artin and Zhang’s theory of noncommutative projective schemes [Reference Artin and ZhangAZ].
$\mathbb{P}^{d}$
, which we call a GL order (see below). Both interpretations build on Artin and Zhang’s theory of noncommutative projective schemes [Reference Artin and ZhangAZ].
Viewing GL weighted projective spaces as module categories allows for further, very fruitful, generalizations which is what we explore in this paper. The idea is rather simple: in [Reference Iyama and LernerIL], all GL orders that were considered were always sheaves on
![]() $\mathbb{P}^{d}$
, now we allow the center to be other varieties.
$\mathbb{P}^{d}$
, now we allow the center to be other varieties.
Definition 1.1. Fix a scheme
![]() $X$
over a field
$X$
over a field
![]() $k$
, and for
$k$
, and for
![]() $i=1,\ldots ,n$
fix prime divisors
$i=1,\ldots ,n$
fix prime divisors
![]() $L_{i}$
on
$L_{i}$
on
![]() $X$
and integer weights
$X$
and integer weights
![]() $p_{i}\geqslant 2$
. The Geigle–Lenzing order
$p_{i}\geqslant 2$
. The Geigle–Lenzing order
![]() $A$
(GL order, for short) with center
$A$
(GL order, for short) with center
![]() $X$
associated to this data is the sheaf of noncommutative algebras
$X$
associated to this data is the sheaf of noncommutative algebras
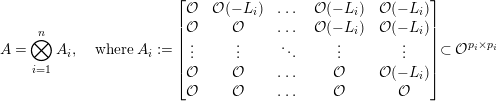 $$\begin{eqnarray}A=\bigotimes _{i=1}^{n}A_{i},\quad \text{where}~A_{i}:=\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]\!\subset {\mathcal{O}}^{p_{i}\times p_{i}}\end{eqnarray}$$
$$\begin{eqnarray}A=\bigotimes _{i=1}^{n}A_{i},\quad \text{where}~A_{i}:=\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]\!\subset {\mathcal{O}}^{p_{i}\times p_{i}}\end{eqnarray}$$
and
![]() ${\mathcal{O}}={\mathcal{O}}_{X}$
.
${\mathcal{O}}={\mathcal{O}}_{X}$
.
The aim of this paper is to study the category
![]() $\mathsf{mod}\,A$
of GL orders
$\mathsf{mod}\,A$
of GL orders
![]() $A$
. In particular, we give a criterion on the existence of tilting sheaves. First, we give a description of
$A$
. In particular, we give a criterion on the existence of tilting sheaves. First, we give a description of
![]() $\mathsf{mod}\,A$
in terms of grid categories
$\mathsf{mod}\,A$
in terms of grid categories
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
, which are constructed from an abelian category
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
, which are constructed from an abelian category
![]() ${\mathcal{A}}$
with endofunctors
${\mathcal{A}}$
with endofunctors
![]() $F_{i}:{\mathcal{A}}\rightarrow {\mathcal{A}}$
and natural transformations
$F_{i}:{\mathcal{A}}\rightarrow {\mathcal{A}}$
and natural transformations
![]() $\unicode[STIX]{x1D702}_{i}:F_{i}\rightarrow \mathsf{id}_{{\mathcal{A}}}$
for
$\unicode[STIX]{x1D702}_{i}:F_{i}\rightarrow \mathsf{id}_{{\mathcal{A}}}$
for
![]() $i=1,\ldots ,n$
. Moreover, we give a sufficient condition for
$i=1,\ldots ,n$
. Moreover, we give a sufficient condition for
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
to have a tilting object. Then, we apply these results to GL orders and obtain the following result, where, for each subset
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
to have a tilting object. Then, we apply these results to GL orders and obtain the following result, where, for each subset
![]() $I\subseteq \{1,\ldots ,n\}$
, we denote
$I\subseteq \{1,\ldots ,n\}$
, we denote
Theorem 1.2. (Theorem 6.7)
Let
![]() $A$
be a GL order on a smooth projective variety over an algebraically closed field
$A$
be a GL order on a smooth projective variety over an algebraically closed field
![]() $k$
, and suppose that
$k$
, and suppose that
![]() $\sum L_{i}$
is a simple normal crossing divisor. Assume that there is a collection of tilting objects
$\sum L_{i}$
is a simple normal crossing divisor. Assume that there is a collection of tilting objects
![]() $T_{I}\in \mathsf{mod}\,{\mathcal{O}}_{I}$
for all
$T_{I}\in \mathsf{mod}\,{\mathcal{O}}_{I}$
for all
![]() $I\subseteq \{1,\ldots ,n\}$
, such that
$I\subseteq \{1,\ldots ,n\}$
, such that
-
∙
 $T_{I}\otimes {\mathcal{O}}_{J}\otimes {\mathcal{O}}(-L_{j})\rightarrow T_{I}\otimes {\mathcal{O}}_{J}$
is injective, whenever
$T_{I}\otimes {\mathcal{O}}_{J}\otimes {\mathcal{O}}(-L_{j})\rightarrow T_{I}\otimes {\mathcal{O}}_{J}$
is injective, whenever
 $I$
,
$I$
,
 $J$
and
$J$
and
 $\{j\}$
are pairwise disjoint;
$\{j\}$
are pairwise disjoint; -
∙
 $\operatorname{Ext}_{{\mathcal{O}}_{J}}^{i}(T_{I}\otimes {\mathcal{O}}_{J},T_{I\cup J})=0$
for all
$\operatorname{Ext}_{{\mathcal{O}}_{J}}^{i}(T_{I}\otimes {\mathcal{O}}_{J},T_{I\cup J})=0$
for all
 $i>0$
, whenever
$i>0$
, whenever
 $I\cap J=\emptyset$
.
$I\cap J=\emptyset$
.
Then,
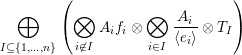 $$\begin{eqnarray}\bigoplus _{I\subseteq \{1,\ldots ,n\}}\left(\mathop{\bigotimes }_{i\not \in I}A_{i}f_{i}\otimes \bigotimes _{i\in I}\frac{A_{i}}{\langle e_{i}\rangle }\otimes T_{I}\right)\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{I\subseteq \{1,\ldots ,n\}}\left(\mathop{\bigotimes }_{i\not \in I}A_{i}f_{i}\otimes \bigotimes _{i\in I}\frac{A_{i}}{\langle e_{i}\rangle }\otimes T_{I}\right)\end{eqnarray}$$
is tilting in
![]() $\mathsf{mod}\,A$
, where
$\mathsf{mod}\,A$
, where
![]() $e_{i}$
and
$e_{i}$
and
![]() $f_{i}$
are matrices of size
$f_{i}$
are matrices of size
![]() $p_{i}\times p_{i}$
with
$p_{i}\times p_{i}$
with
![]() $1$
in the bottom right (respectively top left) position, and
$1$
in the bottom right (respectively top left) position, and
![]() $0$
elsewhere.
$0$
elsewhere.
We apply this result to several concrete projective varieties. For instance, let
![]() $X=\mathbb{P}^{1}\times \mathbb{P}^{1}$
, and let
$X=\mathbb{P}^{1}\times \mathbb{P}^{1}$
, and let
![]() $L_{1}$
and
$L_{1}$
and
![]() $L_{2}$
be
$L_{2}$
be
![]() $(1,1)$
-divisors. Suppose that
$(1,1)$
-divisors. Suppose that
![]() $L_{1}\cap L_{2}=p+q$
. Consider
$L_{1}\cap L_{2}=p+q$
. Consider
Then,
![]() $T_{\emptyset }={\mathcal{O}}\oplus {\mathcal{O}}(1,0)\oplus {\mathcal{O}}(0,1)\oplus {\mathcal{O}}(1,1)$
,
$T_{\emptyset }={\mathcal{O}}\oplus {\mathcal{O}}(1,0)\oplus {\mathcal{O}}(0,1)\oplus {\mathcal{O}}(1,1)$
,
![]() $T_{i}={\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(2)$
for
$T_{i}={\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(2)$
for
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $T_{1,2}={\mathcal{O}}_{p}\oplus {\mathcal{O}}_{q}$
satisfies the assumptions of the theorem. Hence, a tilting object in
$T_{1,2}={\mathcal{O}}_{p}\oplus {\mathcal{O}}_{q}$
satisfies the assumptions of the theorem. Hence, a tilting object in
![]() $\mathsf{mod}\,A$
is
$\mathsf{mod}\,A$
is
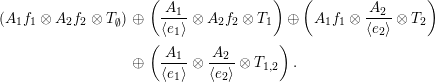 $$\begin{eqnarray}\displaystyle \left(A_{1}f_{1}\otimes A_{2}f_{2}\otimes T_{\emptyset }\right) & \oplus & \displaystyle \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes A_{2}f_{2}\otimes T_{1}\right)\oplus \left(A_{1}f_{1}\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{2}\right)\nonumber\\ \displaystyle & \oplus & \displaystyle \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{1,2}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(A_{1}f_{1}\otimes A_{2}f_{2}\otimes T_{\emptyset }\right) & \oplus & \displaystyle \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes A_{2}f_{2}\otimes T_{1}\right)\oplus \left(A_{1}f_{1}\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{2}\right)\nonumber\\ \displaystyle & \oplus & \displaystyle \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{1,2}\right).\nonumber\end{eqnarray}$$
Our approach is rather general and categorical. In Section 2, we begin with an abelian category
![]() ${\mathcal{A}}$
and an integer
${\mathcal{A}}$
and an integer
![]() $n\geqslant 1$
, we fix endofunctors
$n\geqslant 1$
, we fix endofunctors
![]() $F_{i}$
, natural transformations
$F_{i}$
, natural transformations
![]() $\unicode[STIX]{x1D702}_{i}$
and integer weights
$\unicode[STIX]{x1D702}_{i}$
and integer weights
![]() $p_{i}\geqslant 2$
, and construct a new category
$p_{i}\geqslant 2$
, and construct a new category
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
. In Section 3, we analyze the case
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
. In Section 3, we analyze the case
![]() $n=1$
and, using recollements, give a criterion for this category to have a cotilting object. Our emphasis on cotilting, as opposed to tilting, is because the cotilting criterion is easier to check in
$n=1$
and, using recollements, give a criterion for this category to have a cotilting object. Our emphasis on cotilting, as opposed to tilting, is because the cotilting criterion is easier to check in
![]() $\mathsf{mod}\,A$
. (Abstractly, a dual statement for tilting holds, but it does not seem to apply to the concrete setup as readily.) Due to the existence of Serre duality in
$\mathsf{mod}\,A$
. (Abstractly, a dual statement for tilting holds, but it does not seem to apply to the concrete setup as readily.) Due to the existence of Serre duality in
![]() $\mathsf{mod}\,A$
, cotilting and tilting are actually equivalent, and so this subtlety causes no issues in practice. In Section 4, we analyze the situation for an arbitrary
$\mathsf{mod}\,A$
, cotilting and tilting are actually equivalent, and so this subtlety causes no issues in practice. In Section 4, we analyze the situation for an arbitrary
![]() $n$
. In Section 5, the global dimension of these categories is computed, showing that it often coincides with the global dimension of the original category. In Section 6, we translate the categorical results to orders, to obtain the main result as stated above. Finally, in Section 7, we show how our results may be applied to concrete situations: to Hirzebruch surfaces and to projective spaces. In the
$n$
. In Section 5, the global dimension of these categories is computed, showing that it often coincides with the global dimension of the original category. In Section 6, we translate the categorical results to orders, to obtain the main result as stated above. Finally, in Section 7, we show how our results may be applied to concrete situations: to Hirzebruch surfaces and to projective spaces. In the
![]() $\mathbb{P}^{d}$
case, we show that the tilting bundle we obtain is in fact a generalization of the squid algebra.
$\mathbb{P}^{d}$
case, we show that the tilting bundle we obtain is in fact a generalization of the squid algebra.
2 Setup and notation
Throughout,
![]() $k$
denotes an algebraically closed field. Let
$k$
denotes an algebraically closed field. Let
![]() ${\mathcal{A}}$
be a
${\mathcal{A}}$
be a
![]() $k$
-linear,
$k$
-linear,
![]() $\operatorname{Hom}$
-finite, abelian category. Throughout, we compose morphisms left to right. Fix, for
$\operatorname{Hom}$
-finite, abelian category. Throughout, we compose morphisms left to right. Fix, for
![]() $i=1,\ldots ,n$
, commuting exact functors
$i=1,\ldots ,n$
, commuting exact functors
![]() $F_{i}:{\mathcal{A}}\rightarrow {\mathcal{A}}$
, natural transformations
$F_{i}:{\mathcal{A}}\rightarrow {\mathcal{A}}$
, natural transformations
![]() $\unicode[STIX]{x1D702}_{i}:F_{i}\rightarrow \mathsf{id}_{{\mathcal{A}}}$
and integer weights
$\unicode[STIX]{x1D702}_{i}:F_{i}\rightarrow \mathsf{id}_{{\mathcal{A}}}$
and integer weights
![]() $p_{i}\geqslant 2$
. For any
$p_{i}\geqslant 2$
. For any
![]() $M\in {\mathcal{A}}$
, we denote
$M\in {\mathcal{A}}$
, we denote
instead of the more conventional notation
![]() $\unicode[STIX]{x1D702}_{i,M}$
. Using these data, we now define a new category
$\unicode[STIX]{x1D702}_{i,M}$
. Using these data, we now define a new category
of
![]() $n$
-dimensional grids of size
$n$
-dimensional grids of size
![]() $(p_{1}+1)\times \cdots \times (p_{n}+1)$
of commuting morphisms. To make this precise, we need to introduce some notation. Let
$(p_{1}+1)\times \cdots \times (p_{n}+1)$
of commuting morphisms. To make this precise, we need to introduce some notation. Let
and denote by
![]() $\mathbf{e}_{i}$
the
$\mathbf{e}_{i}$
the
![]() $i$
th basis vector in
$i$
th basis vector in
![]() $\mathbb{Z}^{n}$
.
$\mathbb{Z}^{n}$
.
Throughout, for compact notation, whenever objects or morphisms are indexed by
![]() $S$
we also allow nonpositive indices and interpret them via
$S$
we also allow nonpositive indices and interpret them via
![]() $M_{\mathbf{a}}:=F_{i}M_{\mathbf{a}+p_{i}\mathbf{e}_{i}}$
, and similar for morphisms. Note that the assumption that the
$M_{\mathbf{a}}:=F_{i}M_{\mathbf{a}+p_{i}\mathbf{e}_{i}}$
, and similar for morphisms. Note that the assumption that the
![]() $F_{i}$
commute makes this well defined even if several indices are nonpositive.
$F_{i}$
commute makes this well defined even if several indices are nonpositive.
With this notation, we define objects of
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
to be tuples
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
to be tuples
of objects and morphisms in
![]() ${\mathcal{A}}$
, subject to the following conditions.
${\mathcal{A}}$
, subject to the following conditions.
-
∙ Commutativity condition: for any
 $i,j\in \{1,\ldots ,n\}$
and
$i,j\in \{1,\ldots ,n\}$
and
 $\mathbf{a}\in S$
, we have
$\mathbf{a}\in S$
, we have
 $f_{\mathbf{a}-\mathbf{e}_{i}}^{j}f_{\mathbf{a}}^{i}=f_{\mathbf{a}-\mathbf{e}_{j}}^{i}f_{\mathbf{a}}^{j}$
. That is, the following diagram commutes:
$f_{\mathbf{a}-\mathbf{e}_{i}}^{j}f_{\mathbf{a}}^{i}=f_{\mathbf{a}-\mathbf{e}_{j}}^{i}f_{\mathbf{a}}^{j}$
. That is, the following diagram commutes:
-
∙ Cycle condition: for any
 $i\in \{1,\ldots ,n\}$
and
$i\in \{1,\ldots ,n\}$
and
 $\mathbf{a}\in S$
, we have
$\mathbf{a}\in S$
, we have
 $f_{\mathbf{a}-(p_{i}-1)\mathbf{e}_{i}}^{i}\cdots f_{\mathbf{a}-\mathbf{e}_{i}}^{i}f_{\mathbf{a}}^{i}=\unicode[STIX]{x1D702}_{i}(M_{\mathbf{a}})$
.
$f_{\mathbf{a}-(p_{i}-1)\mathbf{e}_{i}}^{i}\cdots f_{\mathbf{a}-\mathbf{e}_{i}}^{i}f_{\mathbf{a}}^{i}=\unicode[STIX]{x1D702}_{i}(M_{\mathbf{a}})$
.
A morphism
![]() $\unicode[STIX]{x1D711}:(M_{\mathbf{a}},f_{\mathbf{a}}^{i})\rightarrow (N_{\mathbf{a}},g_{\mathbf{a}}^{i})\in {\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
is a set of morphisms
$\unicode[STIX]{x1D711}:(M_{\mathbf{a}},f_{\mathbf{a}}^{i})\rightarrow (N_{\mathbf{a}},g_{\mathbf{a}}^{i})\in {\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
is a set of morphisms
![]() $\unicode[STIX]{x1D711}_{\mathbf{a}}:M_{\mathbf{a}}\rightarrow N_{\mathbf{a}}$
in
$\unicode[STIX]{x1D711}_{\mathbf{a}}:M_{\mathbf{a}}\rightarrow N_{\mathbf{a}}$
in
![]() ${\mathcal{A}}$
with
${\mathcal{A}}$
with
![]() $\mathbf{a}\in S$
, such that the following diagram commutes:
$\mathbf{a}\in S$
, such that the following diagram commutes:
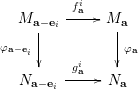
Remark 2.1. A version of the grid category with one weight (see Example 2.2 below) has been studied by Lenzing [Reference LenzingL] under the name category of
![]() $p$
-cycles. His construction, in turn, was inspired by Seshadri’s discussion [Reference SeshadriS] of quasiparabolic structures of filtration length
$p$
-cycles. His construction, in turn, was inspired by Seshadri’s discussion [Reference SeshadriS] of quasiparabolic structures of filtration length
![]() $p$
.
$p$
.
Example 2.2. If
![]() $n=1$
, then objects in
$n=1$
, then objects in
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
are sequences
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
are sequences
such that the composition
is equal to
![]() $\unicode[STIX]{x1D702}(M_{p-d}):FM_{p-d}\rightarrow M_{p-d}$
for all
$\unicode[STIX]{x1D702}(M_{p-d}):FM_{p-d}\rightarrow M_{p-d}$
for all
![]() $0\leqslant d\leqslant p-1$
.
$0\leqslant d\leqslant p-1$
.
In particular, it is worth noting that
![]() ${\mathcal{A}}[\!\sqrt[1]{\unicode[STIX]{x1D702}}]$
is isomorphic to
${\mathcal{A}}[\!\sqrt[1]{\unicode[STIX]{x1D702}}]$
is isomorphic to
![]() ${\mathcal{A}}$
: objects of
${\mathcal{A}}$
: objects of
![]() ${\mathcal{A}}[\!\sqrt[1]{\unicode[STIX]{x1D702}}]$
are diagrams
${\mathcal{A}}[\!\sqrt[1]{\unicode[STIX]{x1D702}}]$
are diagrams
![]() $FM_{1}\xrightarrow[{}]{\unicode[STIX]{x1D702}(M_{1})}M_{1}$
, and thus are uniquely given by an object
$FM_{1}\xrightarrow[{}]{\unicode[STIX]{x1D702}(M_{1})}M_{1}$
, and thus are uniquely given by an object
![]() $M_{1}$
of
$M_{1}$
of
![]() ${\mathcal{A}}$
. One easily sees that the morphism spaces also match.
${\mathcal{A}}$
. One easily sees that the morphism spaces also match.
Example 2.3. Suppose that
![]() $n=2,\;p_{1}=2$
and
$n=2,\;p_{1}=2$
and
![]() $p_{2}=3$
. Then, objects in
$p_{2}=3$
. Then, objects in
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\sqrt[p_{2}]{\unicode[STIX]{x1D702}_{2}}]$
are
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\sqrt[p_{2}]{\unicode[STIX]{x1D702}_{2}}]$
are
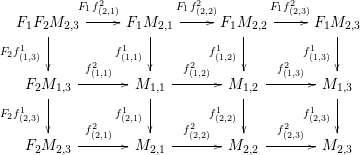
where all of the squares commute and the rows and columns satisfy the cycle conditions.
In this paper, we are primarily concerned with the existence of cotilting objects in
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
.
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
.
Definition 2.4. Let
![]() ${\mathcal{A}}$
be an abelian category. We say that an object
${\mathcal{A}}$
be an abelian category. We say that an object
![]() $T$
in
$T$
in
![]() ${\mathcal{A}}$
is tilting (resp. cotilting), if satisfies the following two conditions.
${\mathcal{A}}$
is tilting (resp. cotilting), if satisfies the following two conditions.
-
∙ Rigidity:
 $\operatorname{Ext}_{{\mathcal{A}}}^{i}(T,T)=0$
for all
$\operatorname{Ext}_{{\mathcal{A}}}^{i}(T,T)=0$
for all
 $i>0$
.
$i>0$
. -
∙ Generation (resp. cogeneration):
 $\operatorname{Ext}_{{\mathcal{A}}}^{i}(T,M)=0$
(resp.
$\operatorname{Ext}_{{\mathcal{A}}}^{i}(T,M)=0$
(resp.
 $\operatorname{Ext}_{{\mathcal{A}}}^{i}(M,T)=0$
) for all
$\operatorname{Ext}_{{\mathcal{A}}}^{i}(M,T)=0$
) for all
 $i\geqslant 0$
implies
$i\geqslant 0$
implies
 $M=0$
.
$M=0$
.
In the next two sections, we focus on proving results regarding cotilting objects, rather than tilting. Analogous results can be derived for the latter; however, the corresponding results are of little practical use in the applications to orders that we have in mind in Sections 6 and 7. However, due to the existence of Serre duality in the order setting, tilting and cotilting objects coincide.
3 Cotilting for the case with only one weight
In this section, we analyze the situation where
![]() $n=1$
, that is, the category
$n=1$
, that is, the category
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Recall that this category was already introduced in Example 2.2. The results we obtain will be useful when we study the general case.
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Recall that this category was already introduced in Example 2.2. The results we obtain will be useful when we study the general case.
We denote by
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
the full subcategory of
${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
the full subcategory of
![]() ${\mathcal{A}}$
with objects given by
${\mathcal{A}}$
with objects given by
We begin by considering the following special case, which will prove to be an important ingredient of the general discussion later. Let
![]() $F=0$
, and
$F=0$
, and
![]() $\unicode[STIX]{x1D702}$
be the zero transformation
$\unicode[STIX]{x1D702}$
be the zero transformation
![]() $F\rightarrow \mathsf{id}_{{\mathcal{A}}}$
. To ease notation, we employ the following convention.
$F\rightarrow \mathsf{id}_{{\mathcal{A}}}$
. To ease notation, we employ the following convention.
Convention 3.1. Whenever
![]() $\unicode[STIX]{x1D702}$
is the zero transformation, we consider it as a natural transformation from the zero functor to the identity functor.
$\unicode[STIX]{x1D702}$
is the zero transformation, we consider it as a natural transformation from the zero functor to the identity functor.
(A priori it would make sense to consider zero transformations between any two functors. However, in this paper, we will soon assume (see 3.8) that
![]() $\unicode[STIX]{x1D702}$
is injective on sufficiently many objects. Thus, for us it makes sense to only consider zero transformations starting in zero functors.)
$\unicode[STIX]{x1D702}$
is injective on sufficiently many objects. Thus, for us it makes sense to only consider zero transformations starting in zero functors.)
In this case,
where
![]() $\vec{A}_{p}$
is the linearly oriented quiver of Dynkin type
$\vec{A}_{p}$
is the linearly oriented quiver of Dynkin type
![]() $A$
and
$A$
and
![]() $p$
vertices and viewed as a (finite) category in the obvious way. We have an exact functor
$p$
vertices and viewed as a (finite) category in the obvious way. We have an exact functor
![]() $\unicode[STIX]{x1D6FF}:{\mathcal{A}}\rightarrow {\mathcal{A}}[\!\sqrt[p]{0}]$
, with
$\unicode[STIX]{x1D6FF}:{\mathcal{A}}\rightarrow {\mathcal{A}}[\!\sqrt[p]{0}]$
, with
which has an exact left adjoint
In the following, we prove that exact adjoint functors are also adjoint with respect to
![]() $\operatorname{Ext}$
. Since the most usual way to see this is to use projective or injective resolutions, which we do not assume to exist here, we give a small argument using Yoneda extension groups.
$\operatorname{Ext}$
. Since the most usual way to see this is to use projective or injective resolutions, which we do not assume to exist here, we give a small argument using Yoneda extension groups.
Lemma 3.2. Let
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{B}}$
be exact categories, and let
${\mathcal{B}}$
be exact categories, and let
![]() $L:{\mathcal{A}}\rightarrow {\mathcal{B}}$
and
$L:{\mathcal{A}}\rightarrow {\mathcal{B}}$
and
![]() $R:{\mathcal{B}}\rightarrow {\mathcal{A}}$
be a pair of exact adjoint functors. Then,
$R:{\mathcal{B}}\rightarrow {\mathcal{A}}$
be a pair of exact adjoint functors. Then,
functorial in
![]() $A\in {\mathcal{A}}$
and
$A\in {\mathcal{A}}$
and
![]() $B\in {\mathcal{B}}$
.
$B\in {\mathcal{B}}$
.
Proof. We view the
![]() $\operatorname{Ext}$
groups as Yoneda
$\operatorname{Ext}$
groups as Yoneda
![]() $\operatorname{Ext}$
groups and use the following notation. Given
$\operatorname{Ext}$
groups and use the following notation. Given
![]() $\mathbb{E}\in \operatorname{Ext}^{i}(A,B)$
and maps
$\mathbb{E}\in \operatorname{Ext}^{i}(A,B)$
and maps
![]() $\unicode[STIX]{x1D6FC}:B\rightarrow B^{\prime }$
and
$\unicode[STIX]{x1D6FC}:B\rightarrow B^{\prime }$
and
![]() $\unicode[STIX]{x1D6FD}:A^{\prime }\rightarrow A$
, we denote by
$\unicode[STIX]{x1D6FD}:A^{\prime }\rightarrow A$
, we denote by
![]() $\unicode[STIX]{x1D6FC}_{\ast }\mathbb{E}\in \operatorname{Ext}^{i}(A,B^{\prime })$
the extension obtained by taking the pushout along
$\unicode[STIX]{x1D6FC}_{\ast }\mathbb{E}\in \operatorname{Ext}^{i}(A,B^{\prime })$
the extension obtained by taking the pushout along
![]() $\unicode[STIX]{x1D6FC}$
and by
$\unicode[STIX]{x1D6FC}$
and by
![]() $\unicode[STIX]{x1D6FD}^{\ast }\mathbb{E}\in \operatorname{Ext}^{i}(A^{\prime },B)$
the extension obtained by taking the pullback along
$\unicode[STIX]{x1D6FD}^{\ast }\mathbb{E}\in \operatorname{Ext}^{i}(A^{\prime },B)$
the extension obtained by taking the pullback along
![]() $\unicode[STIX]{x1D6FD}$
. Note that by [Reference Mac LaneML, Lemma 3.1.6] we have
$\unicode[STIX]{x1D6FD}$
. Note that by [Reference Mac LaneML, Lemma 3.1.6] we have
To prove the lemma, we give two maps, and show that they are mutually inverse to each other. From left to right, let
![]() $\mathbb{E}\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
. Since
$\mathbb{E}\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
. Since
![]() $L$
is exact, we may apply it to
$L$
is exact, we may apply it to
![]() $\mathbb{E}$
, obtaining
$\mathbb{E}$
, obtaining
![]() $L(\mathbb{E})\in \operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,LRB)$
. Now consider the counit of the adjunction
$L(\mathbb{E})\in \operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,LRB)$
. Now consider the counit of the adjunction
![]() $\unicode[STIX]{x1D700}_{B}:LRB\rightarrow B$
. Taking the pushout along this map, we obtain
$\unicode[STIX]{x1D700}_{B}:LRB\rightarrow B$
. Taking the pushout along this map, we obtain
![]() ${\unicode[STIX]{x1D700}_{B}}_{\ast }L(\mathbb{E})\in \operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,B)$
.
${\unicode[STIX]{x1D700}_{B}}_{\ast }L(\mathbb{E})\in \operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,B)$
.
Conversely, from right to left, we send
![]() $\mathbb{E}\in \operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,B)$
to
$\mathbb{E}\in \operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,B)$
to
![]() $\unicode[STIX]{x1D714}_{A}^{\ast }R(\mathbb{E})\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
, where
$\unicode[STIX]{x1D714}_{A}^{\ast }R(\mathbb{E})\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
, where
![]() $\unicode[STIX]{x1D714}_{A}:A\rightarrow RLA$
denotes the unit of the adjunction.
$\unicode[STIX]{x1D714}_{A}:A\rightarrow RLA$
denotes the unit of the adjunction.
Both constructions are well defined on the Yoneda extension groups, and are functorial. It remains to see that they are mutually inverse. Here, we check that going from left to right and then back again one obtains the extension one started with. Checking that this also works the other way around is very similar.
Therefore, let
![]() $\mathbb{E}\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
. Applying
$\mathbb{E}\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
. Applying
![]() $L$
to
$L$
to
![]() $\mathbb{E}$
and sending it to
$\mathbb{E}$
and sending it to
![]() $\operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,B)$
via a pushout along
$\operatorname{Ext}_{{\mathcal{B}}}^{n}(LA,B)$
via a pushout along
![]() $\unicode[STIX]{x1D700}_{B}$
, and then applying
$\unicode[STIX]{x1D700}_{B}$
, and then applying
![]() $R$
and sending it back to
$R$
and sending it back to
![]() $\operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
via the pullback along
$\operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
via the pullback along
![]() $\unicode[STIX]{x1D714}_{A}$
, we obtain
$\unicode[STIX]{x1D714}_{A}$
, we obtain
![]() $\unicode[STIX]{x1D714}_{A}^{\ast }R({\unicode[STIX]{x1D700}_{B}}_{\ast }L(\mathbb{E}))\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
. Since
$\unicode[STIX]{x1D714}_{A}^{\ast }R({\unicode[STIX]{x1D700}_{B}}_{\ast }L(\mathbb{E}))\in \operatorname{Ext}_{{\mathcal{A}}}^{n}(A,RB)$
. Since
![]() $R$
is exact, it commutes with pushouts, so this is the same as applying
$R$
is exact, it commutes with pushouts, so this is the same as applying
![]() $RL$
to
$RL$
to
![]() $\mathbb{E}$
and then taking the pushout along
$\mathbb{E}$
and then taking the pushout along
![]() $R(\unicode[STIX]{x1D700}_{B})$
followed by a pullback along
$R(\unicode[STIX]{x1D700}_{B})$
followed by a pullback along
![]() $\unicode[STIX]{x1D714}_{A}$
. Thus, we have
$\unicode[STIX]{x1D714}_{A}$
. Thus, we have
Moreover,
![]() $\unicode[STIX]{x1D714}$
is a natural transformation
$\unicode[STIX]{x1D714}$
is a natural transformation
![]() $\mathsf{id}\rightarrow RL$
, so
$\mathsf{id}\rightarrow RL$
, so
![]() $\unicode[STIX]{x1D714}_{A}^{\ast }RL(\mathbb{E})\simeq {\unicode[STIX]{x1D714}_{RB}}_{\ast }\mathbb{E}$
. Thus,
$\unicode[STIX]{x1D714}_{A}^{\ast }RL(\mathbb{E})\simeq {\unicode[STIX]{x1D714}_{RB}}_{\ast }\mathbb{E}$
. Thus,
Now, the proof is completed using the general fact for adjoint pairs that
![]() $R(\unicode[STIX]{x1D700}_{B})\circ \unicode[STIX]{x1D714}_{RB}=\mathsf{id}_{RB}$
.◻
$R(\unicode[STIX]{x1D700}_{B})\circ \unicode[STIX]{x1D714}_{RB}=\mathsf{id}_{RB}$
.◻
Applying Lemma 3.2 to the special case of the exact adjoint functors
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}$
and
![]() $\unicode[STIX]{x1D6FF}$
from above, we obtain the following.
$\unicode[STIX]{x1D6FF}$
from above, we obtain the following.
Lemma 3.3. Let
![]() $M,N\in {\mathcal{A}}$
and
$M,N\in {\mathcal{A}}$
and
![]() $i\geqslant 1$
. Then,
$i\geqslant 1$
. Then,
![]() $\operatorname{Ext}_{{\mathcal{A}}}^{i}(M,N)=0$
if and only if
$\operatorname{Ext}_{{\mathcal{A}}}^{i}(M,N)=0$
if and only if
![]() $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{0}]}^{i}(\unicode[STIX]{x1D6FF}M,\unicode[STIX]{x1D6FF}N)=0$
.
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{0}]}^{i}(\unicode[STIX]{x1D6FF}M,\unicode[STIX]{x1D6FF}N)=0$
.
Proof. Since
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}$
are exact,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}$
are exact,
with
![]() $n=\frac{1}{2}p(p+1)$
.◻
$n=\frac{1}{2}p(p+1)$
.◻
Proposition 3.4. If
![]() $T$
is a cotilting object in
$T$
is a cotilting object in
![]() ${\mathcal{A}}$
, then
${\mathcal{A}}$
, then
![]() $\unicode[STIX]{x1D6FF}(T)$
is a cotilting object in
$\unicode[STIX]{x1D6FF}(T)$
is a cotilting object in
![]() ${\mathcal{A}}[\!\sqrt[p]{0}]$
.
${\mathcal{A}}[\!\sqrt[p]{0}]$
.
Proof. By Lemma 3.3 and the fact that
![]() $T$
is cotilting in
$T$
is cotilting in
![]() ${\mathcal{A}}$
, we see that
${\mathcal{A}}$
, we see that
![]() $\unicode[STIX]{x1D6FF}(T)$
is rigid. We now prove that
$\unicode[STIX]{x1D6FF}(T)$
is rigid. We now prove that
![]() $\unicode[STIX]{x1D6FF}(T)$
cogenerates
$\unicode[STIX]{x1D6FF}(T)$
cogenerates
![]() ${\mathcal{A}}[\!\sqrt[p]{0}]$
. Let
${\mathcal{A}}[\!\sqrt[p]{0}]$
. Let
![]() $M\in {\mathcal{A}}[\!\sqrt[p]{0}]$
, and suppose that
$M\in {\mathcal{A}}[\!\sqrt[p]{0}]$
, and suppose that
![]() $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{0}]}^{i}(M,\unicode[STIX]{x1D6FF}(T))=0$
. Then,
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{0}]}^{i}(M,\unicode[STIX]{x1D6FF}(T))=0$
. Then,
and so, since
![]() $T$
cogenerates
$T$
cogenerates
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $M_{1}=\cdots =M_{p}=0$
, that is,
$M_{1}=\cdots =M_{p}=0$
, that is,
![]() $M=0$
.◻
$M=0$
.◻
We now define recollements. These are used to study categories
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
here, and in the next section are also applied to the study of
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
here, and in the next section are also applied to the study of
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
(for an arbitrary
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
(for an arbitrary
![]() $n$
).
$n$
).
Definition 3.5. [Reference Beilinson, Bernstein and DeligneBBD]
Let
![]() ${\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime }$
be abelian categories. A recollement is the following diagram of additive functors:
${\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime }$
be abelian categories. A recollement is the following diagram of additive functors:
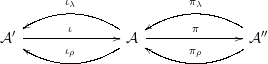
such that
-
(1)
 $(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D704},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}})$
and
$(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D704},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}})$
and
 $(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}})$
are adjoint triples;
$(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}})$
are adjoint triples; -
(2)
 $\unicode[STIX]{x1D704},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D704},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}$
are fully faithful;
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}$
are fully faithful; -
(3)
 $\text{im}\,\unicode[STIX]{x1D704}=\ker \unicode[STIX]{x1D70B}$
.
$\text{im}\,\unicode[STIX]{x1D704}=\ker \unicode[STIX]{x1D70B}$
.
Example 3.6. Let
![]() $A$
be a ring, and let
$A$
be a ring, and let
![]() $e$
be an idempotent. Denote by
$e$
be an idempotent. Denote by
![]() $\mathsf{mod}\,A$
the category of left
$\mathsf{mod}\,A$
the category of left
![]() $A$
-modules. Then, we have the following recollement:
$A$
-modules. Then, we have the following recollement:
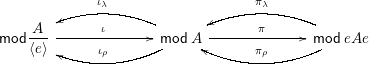
where
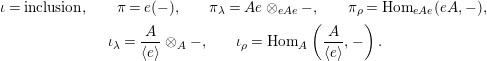 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D704}=\text{inclusion},\!\qquad \unicode[STIX]{x1D70B}=e(-),\!\qquad \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}=Ae\otimes _{eAe}-,\!\qquad \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}=\operatorname{Hom}_{eAe}(eA,-), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}=\frac{A}{\langle e\rangle }\otimes _{A}-,\!\qquad \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}=\operatorname{Hom}_{A}\left(\frac{A}{\langle e\rangle },-\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D704}=\text{inclusion},\!\qquad \unicode[STIX]{x1D70B}=e(-),\!\qquad \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}=Ae\otimes _{eAe}-,\!\qquad \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}=\operatorname{Hom}_{eAe}(eA,-), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}=\frac{A}{\langle e\rangle }\otimes _{A}-,\!\qquad \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}=\operatorname{Hom}_{A}\left(\frac{A}{\langle e\rangle },-\right). & \displaystyle \nonumber\end{eqnarray}$$
If
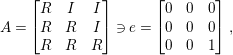 $$\begin{eqnarray}A=\left[\begin{array}{@{}ccc@{}}R & I & I\\ R & R & I\\ R & R & R\end{array}\right]\ni e=\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}A=\left[\begin{array}{@{}ccc@{}}R & I & I\\ R & R & I\\ R & R & R\end{array}\right]\ni e=\left[\begin{array}{@{}ccc@{}}0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1\end{array}\right],\end{eqnarray}$$
where
![]() $R$
is a ring and
$R$
is a ring and
![]() $I$
is an ideal, then
$I$
is an ideal, then
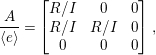 $$\begin{eqnarray}\frac{A}{\langle e\rangle }=\left[\begin{array}{@{}ccc@{}}R/I & 0 & 0\\ R/I & R/I & 0\\ 0 & 0 & 0\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\frac{A}{\langle e\rangle }=\left[\begin{array}{@{}ccc@{}}R/I & 0 & 0\\ R/I & R/I & 0\\ 0 & 0 & 0\end{array}\right],\end{eqnarray}$$
and so the recollement becomes
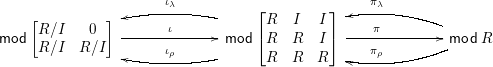
with
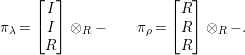 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}=\left[\begin{array}{@{}c@{}}I\\ I\\ R\end{array}\right]\otimes _{R}-\qquad \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}=\left[\begin{array}{@{}c@{}}R\\ R\\ R\end{array}\right]\otimes _{R}-.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}=\left[\begin{array}{@{}c@{}}I\\ I\\ R\end{array}\right]\otimes _{R}-\qquad \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}=\left[\begin{array}{@{}c@{}}R\\ R\\ R\end{array}\right]\otimes _{R}-.\end{eqnarray}$$
We now return to the category
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Recall that we denote by
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Recall that we denote by
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
the subcategory of
${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
the subcategory of
![]() ${\mathcal{A}}$
consisting of all objects on which
${\mathcal{A}}$
consisting of all objects on which
![]() $\unicode[STIX]{x1D702}$
vanishes.
$\unicode[STIX]{x1D702}$
vanishes.
Proposition 3.7. The following is a recollement. (Recall that, by Convention 3.1, on the left side we consider the functor
![]() $0$
, and not the functor
$0$
, and not the functor
![]() $F$
, which is considered in the middle term.)
$F$
, which is considered in the middle term.)
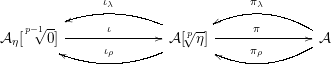
where the functors are defined by the following:
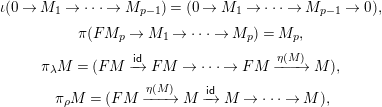 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D704}(0\rightarrow M_{1}\rightarrow \cdots \rightarrow M_{p-1})=(0\rightarrow M_{1}\rightarrow \cdots \rightarrow M_{p-1}\rightarrow 0), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(FM_{p}\rightarrow M_{1}\rightarrow \cdots \rightarrow M_{p})=M_{p}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}M=(FM\xrightarrow[{}]{\mathsf{id}}FM\rightarrow \cdots \rightarrow FM\xrightarrow[{}]{\unicode[STIX]{x1D702}(M)}M), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}M=(FM\xrightarrow[{}]{\unicode[STIX]{x1D702}(M)}M\xrightarrow[{}]{\mathsf{id}}M\rightarrow \cdots \rightarrow M), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D704}(0\rightarrow M_{1}\rightarrow \cdots \rightarrow M_{p-1})=(0\rightarrow M_{1}\rightarrow \cdots \rightarrow M_{p-1}\rightarrow 0), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(FM_{p}\rightarrow M_{1}\rightarrow \cdots \rightarrow M_{p})=M_{p}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}M=(FM\xrightarrow[{}]{\mathsf{id}}FM\rightarrow \cdots \rightarrow FM\xrightarrow[{}]{\unicode[STIX]{x1D702}(M)}M), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}M=(FM\xrightarrow[{}]{\unicode[STIX]{x1D702}(M)}M\xrightarrow[{}]{\mathsf{id}}M\rightarrow \cdots \rightarrow M), & \displaystyle \nonumber\end{eqnarray}$$
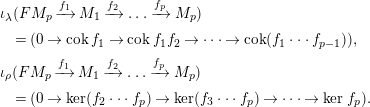 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(FM_{p}\xrightarrow[{}]{f_{1}}M_{1}\xrightarrow[{}]{f_{2}}\ldots \xrightarrow[{}]{f_{p}}M_{p})\nonumber\\ \displaystyle & & \displaystyle \quad =(0\rightarrow \operatorname{cok}f_{1}\rightarrow \operatorname{cok}f_{1}f_{2}\rightarrow \cdots \rightarrow \operatorname{cok}(f_{1}\cdots f_{p-1})),\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}(FM_{p}\xrightarrow[{}]{f_{1}}M_{1}\xrightarrow[{}]{f_{2}}\ldots \xrightarrow[{}]{f_{p}}M_{p})\nonumber\\ \displaystyle & & \displaystyle \quad =(0\rightarrow \ker (f_{2}\cdots f_{p})\rightarrow \ker (f_{3}\cdots f_{p})\rightarrow \cdots \rightarrow \ker f_{p}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(FM_{p}\xrightarrow[{}]{f_{1}}M_{1}\xrightarrow[{}]{f_{2}}\ldots \xrightarrow[{}]{f_{p}}M_{p})\nonumber\\ \displaystyle & & \displaystyle \quad =(0\rightarrow \operatorname{cok}f_{1}\rightarrow \operatorname{cok}f_{1}f_{2}\rightarrow \cdots \rightarrow \operatorname{cok}(f_{1}\cdots f_{p-1})),\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}(FM_{p}\xrightarrow[{}]{f_{1}}M_{1}\xrightarrow[{}]{f_{2}}\ldots \xrightarrow[{}]{f_{p}}M_{p})\nonumber\\ \displaystyle & & \displaystyle \quad =(0\rightarrow \ker (f_{2}\cdots f_{p})\rightarrow \ker (f_{3}\cdots f_{p})\rightarrow \cdots \rightarrow \ker f_{p}).\nonumber\end{eqnarray}$$
Proof. Straightforward. ◻
As we shall see in Proposition 6.1, the recollement from Example 3.6 is a special case of the above more general recollement.
We observe that in the recollement of Proposition 3.7, the functors
![]() $\unicode[STIX]{x1D704},\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D704},\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}$
are all exact. In particular, Lemma 3.2 implies that
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}$
are all exact. In particular, Lemma 3.2 implies that
for all
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
The situation is slightly more involved for
![]() $\unicode[STIX]{x1D704}$
, since none of the functors
$\unicode[STIX]{x1D704}$
, since none of the functors
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
or
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
or
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}$
is exact. To be able to still control its effect on
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}$
is exact. To be able to still control its effect on
![]() $\operatorname{Ext}$
spaces we will need the following assumption.
$\operatorname{Ext}$
spaces we will need the following assumption.
Assumption 3.8. For the remainder of this section, we assume that
![]() ${\mathcal{A}}$
has enough objects
${\mathcal{A}}$
has enough objects
![]() $M$
such that
$M$
such that
![]() $\unicode[STIX]{x1D702}(M)$
is a monomorphism. That is, for all objects
$\unicode[STIX]{x1D702}(M)$
is a monomorphism. That is, for all objects
![]() $X\in {\mathcal{A}}$
, there exists an object
$X\in {\mathcal{A}}$
, there exists an object
![]() $M\in {\mathcal{A}}$
with
$M\in {\mathcal{A}}$
with
![]() $\unicode[STIX]{x1D702}(M)$
a monomorphism, and a surjection
$\unicode[STIX]{x1D702}(M)$
a monomorphism, and a surjection
![]() $M{\twoheadrightarrow}X$
.
$M{\twoheadrightarrow}X$
.
Lemma 3.9. With the above assumption, the subcategory of
![]() ${\mathcal{A}}$
given by
${\mathcal{A}}$
given by
is a resolving subcategory.
The reason for choosing this particular subcategory is because
![]() $\text{im}\,\unicode[STIX]{x1D704}\subseteq {\mathcal{E}}$
, a fact that we need later.
$\text{im}\,\unicode[STIX]{x1D704}\subseteq {\mathcal{E}}$
, a fact that we need later.
Proof. It is clear from the definition that subobjects of objects in
![]() ${\mathcal{E}}$
are in
${\mathcal{E}}$
are in
![]() ${\mathcal{E}}$
again. In particular,
${\mathcal{E}}$
again. In particular,
![]() ${\mathcal{E}}$
is closed under kernels of epimorphisms. Thus, it remains to check that for any object
${\mathcal{E}}$
is closed under kernels of epimorphisms. Thus, it remains to check that for any object
![]() $M\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
there is an epimorphism
$M\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
there is an epimorphism
![]() $E\rightarrow M$
for some
$E\rightarrow M$
for some
![]() $E\in {\mathcal{E}}$
.
$E\in {\mathcal{E}}$
.
Let
![]() $M^{\bullet }=FM_{p}\xrightarrow[{}]{f_{1}}M_{1}\xrightarrow[{}]{f_{2}}\ldots \xrightarrow[{}]{f_{p}}M_{p}\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. For each
$M^{\bullet }=FM_{p}\xrightarrow[{}]{f_{1}}M_{1}\xrightarrow[{}]{f_{2}}\ldots \xrightarrow[{}]{f_{p}}M_{p}\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. For each
![]() $i=1,\ldots ,p$
, let
$i=1,\ldots ,p$
, let
where the
![]() $\unicode[STIX]{x1D702}(M_{i})$
is the
$\unicode[STIX]{x1D702}(M_{i})$
is the
![]() $i$
th arrow from the right. Note that we have a surjective map
$i$
th arrow from the right. Note that we have a surjective map
![]() $\oplus M_{i}^{\bullet }{\twoheadrightarrow}M^{\bullet }$
. Furthermore, by the assumption on
$\oplus M_{i}^{\bullet }{\twoheadrightarrow}M^{\bullet }$
. Furthermore, by the assumption on
![]() ${\mathcal{A}}$
, for all
${\mathcal{A}}$
, for all
![]() $i$
, there exists an
$i$
, there exists an
![]() $X_{i}\in {\mathcal{A}}$
such that
$X_{i}\in {\mathcal{A}}$
such that
![]() $X_{i}{\twoheadrightarrow}M_{i}$
and
$X_{i}{\twoheadrightarrow}M_{i}$
and
![]() $\unicode[STIX]{x1D702}(X_{i})$
is a monomorphism. Since
$\unicode[STIX]{x1D702}(X_{i})$
is a monomorphism. Since
![]() $F$
is exact,
$F$
is exact,
![]() $F(X_{i}){\twoheadrightarrow}F(M_{i})$
, and so
$F(X_{i}){\twoheadrightarrow}F(M_{i})$
, and so
with
![]() $X_{i}^{\bullet }\in {\mathcal{E}}$
. Thus, we have
$X_{i}^{\bullet }\in {\mathcal{E}}$
. Thus, we have
![]() $\oplus X_{i}^{\bullet }{\twoheadrightarrow}M^{\bullet }$
, and we are done.◻
$\oplus X_{i}^{\bullet }{\twoheadrightarrow}M^{\bullet }$
, and we are done.◻
Lemma 3.10.
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
is exact on
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
is exact on
![]() ${\mathcal{E}}$
.
${\mathcal{E}}$
.
Proof. Let
![]() $0\rightarrow (X,f)\rightarrow (Y,g)\rightarrow (Z,h)\rightarrow 0$
be an exact sequence in
$0\rightarrow (X,f)\rightarrow (Y,g)\rightarrow (Z,h)\rightarrow 0$
be an exact sequence in
![]() ${\mathcal{E}}$
. For each
${\mathcal{E}}$
. For each
![]() $i=1,\ldots ,p-1$
, we end up with the following commutative diagram, where all rows and columns are exact:
$i=1,\ldots ,p-1$
, we end up with the following commutative diagram, where all rows and columns are exact:
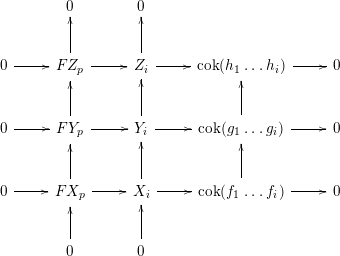
From the snake lemma we see that
is exact, and so we are done. ◻
These two lemmas, together with Lemma 3.2, give us the following.
Proposition 3.11. Let
![]() $M\in {\mathcal{E}}$
, and let
$M\in {\mathcal{E}}$
, and let
![]() $N\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
. Then, for any
$N\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
. Then, for any
![]() $n$
we have
$n$
we have
In particular, for
![]() $M,N\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
one obtains
$M,N\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
one obtains
Proof. By the two lemmas above, we know that
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
and
![]() $\unicode[STIX]{x1D704}$
form a pair of exact adjoint functors between the exact categories
$\unicode[STIX]{x1D704}$
form a pair of exact adjoint functors between the exact categories
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
. Thus, it follows from Lemma 3.2 that
${\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
. Thus, it follows from Lemma 3.2 that
Now, since
![]() ${\mathcal{E}}$
is resolving in
${\mathcal{E}}$
is resolving in
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, we have
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, we have
for
![]() $X,Y\in {\mathcal{E}}$
. In particular,
$X,Y\in {\mathcal{E}}$
. In particular,
The “in particular” part now follows, since
Proposition 3.12. Suppose that
![]() $T$
is a cotilting object in
$T$
is a cotilting object in
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
and
${\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
and
![]() $U$
is cotilting in
$U$
is cotilting in
![]() ${\mathcal{A}}$
. Then,
${\mathcal{A}}$
. Then,
![]() $E=\unicode[STIX]{x1D704}T\oplus \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U$
is cotilting in
$E=\unicode[STIX]{x1D704}T\oplus \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U$
is cotilting in
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
if and only if
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
if and only if
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D704}T)=0$
for all
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D704}T)=0$
for all
![]() $i>0$
.
$i>0$
.
Proof. Cogeneration: suppose that
![]() $\operatorname{Ext}^{i}(M,E)=0$
for all
$\operatorname{Ext}^{i}(M,E)=0$
for all
![]() $i\geqslant 0$
. Then,
$i\geqslant 0$
. Then,
![]() $0=\operatorname{Ext}^{i}(M,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}M,U)$
, and since
$0=\operatorname{Ext}^{i}(M,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}M,U)$
, and since
![]() $U$
is cogenerating this implies
$U$
is cogenerating this implies
![]() $\unicode[STIX]{x1D70B}M=0$
. In this case,
$\unicode[STIX]{x1D70B}M=0$
. In this case,
![]() $M\simeq \unicode[STIX]{x1D704}N$
for some
$M\simeq \unicode[STIX]{x1D704}N$
for some
![]() $N$
. However, then
$N$
. However, then
![]() $0=\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}N,\unicode[STIX]{x1D704}T)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D704}N,T)=\operatorname{Ext}^{i}(N,T)$
implies, using that
$0=\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}N,\unicode[STIX]{x1D704}T)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D704}N,T)=\operatorname{Ext}^{i}(N,T)$
implies, using that
![]() $T$
is cogenerating, that
$T$
is cogenerating, that
![]() $N=0$
, and so
$N=0$
, and so
![]() $M=0$
.
$M=0$
.
Rigidity: for
![]() $i>0$
, we have
$i>0$
, we have
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}T,\unicode[STIX]{x1D704}T)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D704}T,T)=\operatorname{Ext}^{i}(T,T)=0$
, and similarly
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}T,\unicode[STIX]{x1D704}T)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D704}T,T)=\operatorname{Ext}^{i}(T,T)=0$
, and similarly
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,U)=\operatorname{Ext}^{i}(U,U)=0$
. Moreover,
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,U)=\operatorname{Ext}^{i}(U,U)=0$
. Moreover,
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}T,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D704}T,U)=\operatorname{Ext}^{i}(0,U)=0$
. Finally, by assumption,
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D704}T,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U)=\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D704}T,U)=\operatorname{Ext}^{i}(0,U)=0$
. Finally, by assumption,
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D704}T)=0$
, and so we are done.◻
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D704}T)=0$
, and so we are done.◻
We now analyze this condition further. We define an exact functor
which has left and right adjoints
Proposition 3.13. Let
![]() $N\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
, and let
$N\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
, and let
![]() $M\in {\mathcal{A}}$
. Then,
$M\in {\mathcal{A}}$
. Then,
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}M,\unicode[STIX]{x1D704}N)=0$
for all
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}M,\unicode[STIX]{x1D704}N)=0$
for all
![]() $i>0$
if
$i>0$
if
-
∙
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\ker \unicode[STIX]{x1D702}(M),N)=0$
for all
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\ker \unicode[STIX]{x1D702}(M),N)=0$
for all
 $i\geqslant 0$
and
$i\geqslant 0$
and -
∙
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\operatorname{cok}\unicode[STIX]{x1D702}(M),N)=0$
for all
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\operatorname{cok}\unicode[STIX]{x1D702}(M),N)=0$
for all
 $i>0$
.
$i>0$
.
Proof. We have the following exact sequence:
which we break up as follows:
Since for all
![]() $i\geqslant 0$
$i\geqslant 0$
the first sequence implies that
Inserting this in the long exact sequence obtained from the second short exact sequence above, we obtain
from which the proposition follows. ◻
Theorem 3.14. Suppose that
![]() $T$
is cotilting in
$T$
is cotilting in
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
and
${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
and
![]() $U$
is cotilting in
$U$
is cotilting in
![]() ${\mathcal{A}}$
. If
${\mathcal{A}}$
. If
-
∙
 $\unicode[STIX]{x1D702}(U)$
is injective, and
$\unicode[STIX]{x1D702}(U)$
is injective, and -
∙
 $\operatorname{Ext}_{{\mathcal{A}}_{\unicode[STIX]{x1D702}}}^{i}(\operatorname{cok}\unicode[STIX]{x1D702}(U),T)=0$
for all
$\operatorname{Ext}_{{\mathcal{A}}_{\unicode[STIX]{x1D702}}}^{i}(\operatorname{cok}\unicode[STIX]{x1D702}(U),T)=0$
for all
 $i>0$
,
$i>0$
,
then
![]() $\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FF}(T)\oplus \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U$
is cotilting
$\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FF}(T)\oplus \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U$
is cotilting
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
.
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
.
Proof. From Proposition 3.12 we require
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FF}T)=0$
. Now apply Proposition 3.13 with
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}U,\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FF}T)=0$
. Now apply Proposition 3.13 with
![]() $M=U$
and
$M=U$
and
![]() $N=\unicode[STIX]{x1D6FF}(T)$
. The first assumption of 3.12 holds since
$N=\unicode[STIX]{x1D6FF}(T)$
. The first assumption of 3.12 holds since
![]() $\unicode[STIX]{x1D702}(U)$
is injective. For the second assumption, note that
$\unicode[STIX]{x1D702}(U)$
is injective. For the second assumption, note that
4 Cotilting in the general case
In this section, we turn our attention to the more general category
We give a criterion for this category to have a cotilting object.
For each
![]() $I\subseteq \{1,\ldots ,n\}$
, we define the following full subcategory of
$I\subseteq \{1,\ldots ,n\}$
, we define the following full subcategory of
![]() ${\mathcal{A}}$
:
${\mathcal{A}}$
:
Furthermore, assume that each such
![]() ${\mathcal{A}}_{I}$
has a cotilting object
${\mathcal{A}}_{I}$
has a cotilting object
![]() $T_{I}$
. In particular,
$T_{I}$
. In particular,
![]() $T_{\emptyset }$
is a cotilting object in
$T_{\emptyset }$
is a cotilting object in
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
Before we proceed, we need to introduce several new categories, just as we did in Section 3, whose cotilting objects will be used to construct the cotilting object we are seeking.
For
![]() $H,I,J\subseteq \{1,\ldots ,n\}$
with
$H,I,J\subseteq \{1,\ldots ,n\}$
with
![]() $H=\{a_{1},\ldots ,a_{m}\}\subseteq I$
and
$H=\{a_{1},\ldots ,a_{m}\}\subseteq I$
and
![]() $J=\left\{b_{1},\ldots ,b_{\ell }\right\}$
with
$J=\left\{b_{1},\ldots ,b_{\ell }\right\}$
with
![]() $J\cap I=\emptyset$
, let
$J\cap I=\emptyset$
, let
We have, for any
![]() $K=\{c_{1},\ldots ,c_{i}\}\subseteq \{1,\ldots ,n\}$
satisfying
$K=\{c_{1},\ldots ,c_{i}\}\subseteq \{1,\ldots ,n\}$
satisfying
![]() $K\cap (I\cup J)=\emptyset$
, a restriction functor
$K\cap (I\cup J)=\emptyset$
, a restriction functor
which is well defined since the
![]() $F_{i}$
commute.
$F_{i}$
commute.
If either
![]() $J$
or
$J$
or
![]() $H$
is empty, we leave them out from the notation.
$H$
is empty, we leave them out from the notation.
Construction 4.1. The category
![]() ${\mathcal{A}}_{I}[\unicode[STIX]{x1D702}^{\emptyset },0^{H}]={\mathcal{A}}_{I}[0^{H}]$
has a special tilting object
${\mathcal{A}}_{I}[\unicode[STIX]{x1D702}^{\emptyset },0^{H}]={\mathcal{A}}_{I}[0^{H}]$
has a special tilting object
![]() $T_{I}^{H}$
constructed iteratively from
$T_{I}^{H}$
constructed iteratively from
![]() $T_{I}$
using the functor
$T_{I}$
using the functor
![]() $\unicode[STIX]{x1D6FF}$
from Section 3. Explicitly, we start with
$\unicode[STIX]{x1D6FF}$
from Section 3. Explicitly, we start with
![]() $T_{I}^{\emptyset }=T_{I}$
, and set
$T_{I}^{\emptyset }=T_{I}$
, and set
![]() $T_{I}^{H}=\unicode[STIX]{x1D6FF}T_{I}^{H\setminus \{h\}}$
for some
$T_{I}^{H}=\unicode[STIX]{x1D6FF}T_{I}^{H\setminus \{h\}}$
for some
![]() $h\in H$
, where
$h\in H$
, where
is as in the beginning of Section 3. (One may convince oneself that the result of this iterative construction does not depend on the order.)
Let
![]() $H,I,J$
be as above, and let
$H,I,J$
be as above, and let
![]() $a,b\in H$
. We have the following diagram where every row and column is a recollement:
$a,b\in H$
. We have the following diagram where every row and column is a recollement:
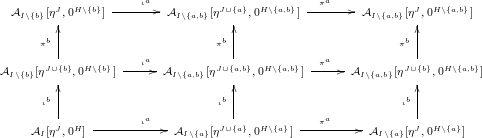
Remark 4.2. Note that we have abused notation slightly by calling many different functors
![]() $\unicode[STIX]{x1D704}^{a}$
. However, no confusion should arise as they all have different domains and codomains, and the correct one is hence clear from context. The same applies to
$\unicode[STIX]{x1D704}^{a}$
. However, no confusion should arise as they all have different domains and codomains, and the correct one is hence clear from context. The same applies to
![]() $\unicode[STIX]{x1D70B}^{a}$
and
$\unicode[STIX]{x1D70B}^{a}$
and
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{a}$
as well.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{a}$
as well.
Lemma 4.3. In the diagram of recollements above, all of the squares (including original functors and adjoint functors) commute, except
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}$
and
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}$
and
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
. In particular, the following three equalities hold, which we will use later:
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}$
. In particular, the following three equalities hold, which we will use later:
-
(i)
 $\unicode[STIX]{x1D704}^{a}\unicode[STIX]{x1D704}^{b}=\unicode[STIX]{x1D704}^{b}\unicode[STIX]{x1D704}^{a}$
(i.e. the left lower square of the diagram commutes);
$\unicode[STIX]{x1D704}^{a}\unicode[STIX]{x1D704}^{b}=\unicode[STIX]{x1D704}^{b}\unicode[STIX]{x1D704}^{a}$
(i.e. the left lower square of the diagram commutes); -
(ii)
 $\unicode[STIX]{x1D704}^{a}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}\unicode[STIX]{x1D704}^{a}$
;
$\unicode[STIX]{x1D704}^{a}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}\unicode[STIX]{x1D704}^{a}$
; -
(iii)
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{a}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{a}$
.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{a}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{b}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{a}$
.
Proof. This is a simple, straightforward calculation. ◻
In light of this lemma, we define, for
![]() $H=\left\{a_{1},\ldots ,a_{h}\right\}\subseteq \{1,\ldots ,n\}$
and an object
$H=\left\{a_{1},\ldots ,a_{h}\right\}\subseteq \{1,\ldots ,n\}$
and an object
![]() $M$
in an appropriate category,
$M$
in an appropriate category,
Similarly, we define
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{H}$
and
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{H}$
and
![]() $\unicode[STIX]{x1D70B}^{H}$
.
$\unicode[STIX]{x1D70B}^{H}$
.
Similarly to the case with only one weight, we need to control how the adjoint pair
![]() $(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}^{a},\unicode[STIX]{x1D704}^{a})$
behaves with respect to
$(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}^{a},\unicode[STIX]{x1D704}^{a})$
behaves with respect to
![]() $\operatorname{Ext}$
. We therefore need a more general version of the assumption used earlier.
$\operatorname{Ext}$
. We therefore need a more general version of the assumption used earlier.
Assumption 4.4. From now on, assume that for all
![]() $I\subseteq \{1,\ldots ,n\}$
and
$I\subseteq \{1,\ldots ,n\}$
and
![]() $a\in \{1,\ldots ,n\}\setminus I$
, the category
$a\in \{1,\ldots ,n\}\setminus I$
, the category
![]() ${\mathcal{A}}_{I}$
has enough objects
${\mathcal{A}}_{I}$
has enough objects
![]() $M$
such that
$M$
such that
![]() $\unicode[STIX]{x1D702}_{a}(M)$
is a monomorphism.
$\unicode[STIX]{x1D702}_{a}(M)$
is a monomorphism.
Lemma 4.5. Let
![]() $H,I,J\subseteq \{1,\ldots ,n\}$
, with
$H,I,J\subseteq \{1,\ldots ,n\}$
, with
![]() $H\subseteq I$
and
$H\subseteq I$
and
![]() $J\cap I=\emptyset$
. Suppose that
$J\cap I=\emptyset$
. Suppose that
![]() $M,N\in {\mathcal{A}}_{I}[\unicode[STIX]{x1D702}^{J},0^{H}]$
. Then, for all
$M,N\in {\mathcal{A}}_{I}[\unicode[STIX]{x1D702}^{J},0^{H}]$
. Then, for all
![]() $a\in H$
and
$a\in H$
and
![]() $i\geqslant 0$
,
$i\geqslant 0$
,
Proof. By Assumption 4.4, we have that
![]() ${\mathcal{A}}_{I\setminus \{a\}}$
has enough objects on which
${\mathcal{A}}_{I\setminus \{a\}}$
has enough objects on which
![]() $\unicode[STIX]{x1D702}_{a}$
is monomorphism. Similarly to the proof of Lemma 3.9, one sees that this implies that also
$\unicode[STIX]{x1D702}_{a}$
is monomorphism. Similarly to the proof of Lemma 3.9, one sees that this implies that also
![]() ${\mathcal{A}}_{I\setminus \{a\}}[\unicode[STIX]{x1D702}^{J},0^{H\setminus \{a\}}]$
has enough objects such that
${\mathcal{A}}_{I\setminus \{a\}}[\unicode[STIX]{x1D702}^{J},0^{H\setminus \{a\}}]$
has enough objects such that
![]() $\unicode[STIX]{x1D702}_{a}$
is monomorphism. The result then follows from 3.11 and the observation that
$\unicode[STIX]{x1D702}_{a}$
is monomorphism. The result then follows from 3.11 and the observation that
Lemma 4.6. Let
![]() $J\subseteq I\subseteq \{1,\ldots ,n\}$
. For
$J\subseteq I\subseteq \{1,\ldots ,n\}$
. For
![]() $T_{I}^{I}$
as defined in Construction 4.1, we have
$T_{I}^{I}$
as defined in Construction 4.1, we have
for all
![]() $i>0$
, if
$i>0$
, if
-
∙
 $\unicode[STIX]{x1D702}_{a}(M|_{J^{\prime }})$
is injective for all
$\unicode[STIX]{x1D702}_{a}(M|_{J^{\prime }})$
is injective for all
 $J^{\prime }\subset J$
and
$J^{\prime }\subset J$
and
 $a\in J\setminus J^{\prime }$
,
$a\in J\setminus J^{\prime }$
, -
∙
 $\operatorname{Ext}^{i}(M|_{J},T_{I}^{I\setminus J})=0$
.
$\operatorname{Ext}^{i}(M|_{J},T_{I}^{I\setminus J})=0$
.
Proof. For all
![]() $a\in J$
,
$a\in J$
,
Hence, using Proposition 3.13, we see that
![]() $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J}M,\unicode[STIX]{x1D704}^{J}T_{I}^{I})=0$
for all
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J}M,\unicode[STIX]{x1D704}^{J}T_{I}^{I})=0$
for all
![]() $i>0$
, if
$i>0$
, if
-
∙
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\ker \unicode[STIX]{x1D702}_{a}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}M),\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I})=0$
for
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\ker \unicode[STIX]{x1D702}_{a}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}M),\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I})=0$
for
 $i\geqslant 0$
and
$i\geqslant 0$
and -
∙
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\operatorname{cok}\unicode[STIX]{x1D702}_{a}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}M),\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I})=0$
for
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}\operatorname{cok}\unicode[STIX]{x1D702}_{a}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}M),\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I})=0$
for
 $i>0$
.
$i>0$
.
Since
the two conditions become
-
∙
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}\ker \unicode[STIX]{x1D702}_{a}M,\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I\setminus \{a\}})=0$
for
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}\ker \unicode[STIX]{x1D702}_{a}M,\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I\setminus \{a\}})=0$
for
 $i\geqslant 0$
and
$i\geqslant 0$
and -
∙
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}M|_{\{a\}},\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I\setminus \{a\}})=0$
for
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{J\setminus \{a\}}M|_{\{a\}},\unicode[STIX]{x1D704}^{J\setminus \{a\}}T_{I}^{I\setminus \{a\}})=0$
for
 $i>0$
.
$i>0$
.
Now repeat this procedure
![]() $|J|-1$
more times to get the result.◻
$|J|-1$
more times to get the result.◻
Theorem 4.7. Let
![]() ${\mathcal{A}}$
be an abelian category equipped with endofunctors
${\mathcal{A}}$
be an abelian category equipped with endofunctors
![]() $F_{i}$
and natural transformation
$F_{i}$
and natural transformation
![]() $\unicode[STIX]{x1D702}_{i}$
as in Section 2, satisfying Assumption 4.4. Assume that there are cotilting objects
$\unicode[STIX]{x1D702}_{i}$
as in Section 2, satisfying Assumption 4.4. Assume that there are cotilting objects
![]() $T_{H}$
in
$T_{H}$
in
![]() ${\mathcal{A}}_{H}$
, such that for all
${\mathcal{A}}_{H}$
, such that for all
![]() $H\cap J=\emptyset$
and
$H\cap J=\emptyset$
and
![]() $a\not \in H\cup J$
,
$a\not \in H\cup J$
,
-
∙
 $\unicode[STIX]{x1D702}_{a}(T_{H}|_{J})$
is injective,
$\unicode[STIX]{x1D702}_{a}(T_{H}|_{J})$
is injective, -
∙
 $\operatorname{Ext}_{{\mathcal{A}}_{H\cup J}}^{i}(T_{H}|_{J},T_{H\cup J})=0$
for all
$\operatorname{Ext}_{{\mathcal{A}}_{H\cup J}}^{i}(T_{H}|_{J},T_{H\cup J})=0$
for all
 $i>0$
.
$i>0$
.
Then, with
![]() $T_{H}^{H}$
as defined in Construction 4.1, and the functors
$T_{H}^{H}$
as defined in Construction 4.1, and the functors
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{[1,n]\setminus H}$
and
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}^{[1,n]\setminus H}$
and
![]() $\unicode[STIX]{x1D704}^{H}$
as explained below Lemma 4.3, the object
$\unicode[STIX]{x1D704}^{H}$
as explained below Lemma 4.3, the object
is a cotilting object in
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
.
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
.
Proof. First, we introduce the following notation: for
![]() $I\subseteq \{1,\ldots ,n\}$
, let
$I\subseteq \{1,\ldots ,n\}$
, let
![]() $\bar{I}:=[1,n]\setminus I$
.
$\bar{I}:=[1,n]\setminus I$
.
Rigidity: we compute
for all
![]() $H,I\subseteq \{1,\ldots ,n\}$
and
$H,I\subseteq \{1,\ldots ,n\}$
and
![]() $i\geqslant 1$
. If
$i\geqslant 1$
. If
![]() $H\cap \bar{I}\neq \emptyset$
, then using Lemma 4.3,
$H\cap \bar{I}\neq \emptyset$
, then using Lemma 4.3,
where
![]() $a\in H\cap \bar{I}$
, since
$a\in H\cap \bar{I}$
, since
![]() $\unicode[STIX]{x1D70B}^{a}\unicode[STIX]{x1D704}^{a}=0$
. Thus, we consider the case where
$\unicode[STIX]{x1D70B}^{a}\unicode[STIX]{x1D704}^{a}=0$
. Thus, we consider the case where
![]() $H\cap \bar{I}=\emptyset$
or, equivalently,
$H\cap \bar{I}=\emptyset$
or, equivalently,
![]() $H\subseteq I$
.
$H\subseteq I$
.
If
![]() $I=H$
, then we use
$I=H$
, then we use
![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D704}=\mathsf{id}$
to obtain
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D704}=\mathsf{id}$
to obtain
since
![]() $T_{H}^{H}$
is cotilting.
$T_{H}^{H}$
is cotilting.
Finally, suppose that
![]() $H\subset I$
, and let
$H\subset I$
, and let
![]() $J=I\setminus H$
. Then, we have
$J=I\setminus H$
. Then, we have
By Lemma 4.6, this vanishes when
-
∙
 $\unicode[STIX]{x1D702}_{a}(T_{H}^{H}|_{J^{\prime }})$
is injective for all
$\unicode[STIX]{x1D702}_{a}(T_{H}^{H}|_{J^{\prime }})$
is injective for all
 $J^{\prime }\subset J$
and
$J^{\prime }\subset J$
and
 $a\in J\setminus J^{\prime }$
,
$a\in J\setminus J^{\prime }$
, -
∙
 $\operatorname{Ext}^{i}(T_{H}^{H}|_{J},T_{I}^{I\setminus J})=\operatorname{Ext}^{i}(T_{H}^{H}|_{J},T_{I}^{H})=0$
for all
$\operatorname{Ext}^{i}(T_{H}^{H}|_{J},T_{I}^{I\setminus J})=\operatorname{Ext}^{i}(T_{H}^{H}|_{J},T_{I}^{H})=0$
for all
 $i>0$
.
$i>0$
.
Thus, rigidity follows from the assumptions of the theorem and Lemma 3.3 applied
![]() $|H|$
times.
$|H|$
times.
Cogeneration: suppose that
![]() $\operatorname{Ext}^{i}(M,T)=0$
for all
$\operatorname{Ext}^{i}(M,T)=0$
for all
![]() $i\geqslant 0$
. We aim to show
$i\geqslant 0$
. We aim to show
![]() $M=0$
. We do so by proving that for all
$M=0$
. We do so by proving that for all
![]() $I\subseteq \{1,\ldots ,n\}$
, we have
$I\subseteq \{1,\ldots ,n\}$
, we have
![]() $\unicode[STIX]{x1D70B}^{I}M=0$
. Note first that
$\unicode[STIX]{x1D70B}^{I}M=0$
. Note first that
and so
![]() $\unicode[STIX]{x1D70B}^{[1,n]}M=0$
. We proceed by reverse induction on
$\unicode[STIX]{x1D70B}^{[1,n]}M=0$
. We proceed by reverse induction on
![]() $|I|$
.
$|I|$
.
Suppose that
![]() $\unicode[STIX]{x1D70B}^{J}M=0$
for all
$\unicode[STIX]{x1D70B}^{J}M=0$
for all
![]() $|J|\geqslant k+1$
. Let
$|J|\geqslant k+1$
. Let
![]() $I\subseteq \{1,\ldots ,n\}$
, such that
$I\subseteq \{1,\ldots ,n\}$
, such that
![]() $|I|=k$
. Then, for all
$|I|=k$
. Then, for all
![]() $a\in \bar{I}$
, we have
$a\in \bar{I}$
, we have
![]() $\unicode[STIX]{x1D70B}^{a}\unicode[STIX]{x1D70B}^{I}M=0$
, so
$\unicode[STIX]{x1D70B}^{a}\unicode[STIX]{x1D70B}^{I}M=0$
, so
![]() $\unicode[STIX]{x1D70B}^{I}M=\unicode[STIX]{x1D704}^{a}N^{\prime }$
for some
$\unicode[STIX]{x1D70B}^{I}M=\unicode[STIX]{x1D704}^{a}N^{\prime }$
for some
![]() $N^{\prime }$
. Hence,
$N^{\prime }$
. Hence,
![]() $\unicode[STIX]{x1D70B}^{I}M=\unicode[STIX]{x1D704}^{\bar{I}}N$
for some
$\unicode[STIX]{x1D70B}^{I}M=\unicode[STIX]{x1D704}^{\bar{I}}N$
for some
![]() $N$
.
$N$
.
and so
![]() $N=0$
, and hence
$N=0$
, and hence
![]() $\unicode[STIX]{x1D70B}^{I}M=0$
for all
$\unicode[STIX]{x1D70B}^{I}M=0$
for all
![]() $\unicode[STIX]{x1D70B}^{I}$
, with
$\unicode[STIX]{x1D70B}^{I}$
, with
![]() $|I|=k$
. Therefore,
$|I|=k$
. Therefore,
![]() $\unicode[STIX]{x1D70B}^{I}M=0$
for all
$\unicode[STIX]{x1D70B}^{I}M=0$
for all
![]() $I\subseteq \{1,\ldots ,n\}$
, in particular
$I\subseteq \{1,\ldots ,n\}$
, in particular
![]() $\unicode[STIX]{x1D70B}^{\emptyset }M=M=0$
.◻
$\unicode[STIX]{x1D70B}^{\emptyset }M=M=0$
.◻
5 Global dimension
In this section, we study the global dimension of the categories
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. The main aim is Theorem 5.7, showing that under certain assumptions (the most important of which is that
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. The main aim is Theorem 5.7, showing that under certain assumptions (the most important of which is that
![]() $F$
is an autoequivalence), the global dimension of
$F$
is an autoequivalence), the global dimension of
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
equals that of
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
equals that of
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
We start by considering the categories on the left side of the recollement of Proposition 3.7. (The abelian category here is called
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
because these are the categories we want to apply this to. However, for this lemma this is just an arbitrary abelian category.)
${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
because these are the categories we want to apply this to. However, for this lemma this is just an arbitrary abelian category.)
Lemma 5.1. Let
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
be abelian, and let
${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
be abelian, and let
![]() $p\geqslant 2$
. Then,
$p\geqslant 2$
. Then,
-
∙
 $\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]\leqslant \operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
(and in fact we have equality unless
$\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]\leqslant \operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
(and in fact we have equality unless
 $p=2$
);
$p=2$
); -
∙ if
 $M=[0\rightarrow M_{1}\overset{f_{2}^{M}}{\rightarrow }\cdots \overset{f_{p-1}^{M}}{\rightarrow }M_{p-1}]\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
, such that all morphisms
$M=[0\rightarrow M_{1}\overset{f_{2}^{M}}{\rightarrow }\cdots \overset{f_{p-1}^{M}}{\rightarrow }M_{p-1}]\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
, such that all morphisms
 $f_{2}^{M},\ldots ,f_{p-1}^{M}$
are epi, then
$f_{2}^{M},\ldots ,f_{p-1}^{M}$
are epi, then
 $\operatorname{inj.dim}M\leqslant \operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}$
.
$\operatorname{inj.dim}M\leqslant \operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}$
.
We do not prove this lemma directly here, but the further discussion throughout the first half of this section results in an inductive proof. See Remark 5.5.
That means that for now, we assume that the lemma holds for a given
![]() $p$
. Note that this is justified for
$p$
. Note that this is justified for
![]() $p=2$
. (In that case
$p=2$
. (In that case
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]={\mathcal{A}}_{\unicode[STIX]{x1D702}}$
.) However, since our aim is not only the inductive proof, we now consider the general case, that is, categories
${\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]={\mathcal{A}}_{\unicode[STIX]{x1D702}}$
.) However, since our aim is not only the inductive proof, we now consider the general case, that is, categories
![]() $\mathscr{A}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Throughout, the following morphisms and resulting exact sequences will play a role.
$\mathscr{A}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Throughout, the following morphisms and resulting exact sequences will play a role.
Observation 5.2. Let
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D702}$
be as in Proposition 3.7. Let
$\unicode[STIX]{x1D702}$
be as in Proposition 3.7. Let
![]() $X\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
.
$X\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
.
-
(i) For the unit
 $\unicode[STIX]{x1D700}_{X}:X\rightarrow \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70B}X$
, we have We note that all of the nonzero maps in
$\unicode[STIX]{x1D700}_{X}:X\rightarrow \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70B}X$
, we have We note that all of the nonzero maps in $$\begin{eqnarray}\displaystyle \ker \unicode[STIX]{x1D700}_{X} & = & \displaystyle \unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}X\qquad \text{and}\nonumber\\ \displaystyle \operatorname{cok}\unicode[STIX]{x1D700}_{X} & = & \displaystyle \unicode[STIX]{x1D704}(0\rightarrow \operatorname{cok}(f_{2}^{X}\cdots f_{p}^{X})\rightarrow \cdots \rightarrow \operatorname{cok}f_{p}^{X}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ker \unicode[STIX]{x1D700}_{X} & = & \displaystyle \unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}X\qquad \text{and}\nonumber\\ \displaystyle \operatorname{cok}\unicode[STIX]{x1D700}_{X} & = & \displaystyle \unicode[STIX]{x1D704}(0\rightarrow \operatorname{cok}(f_{2}^{X}\cdots f_{p}^{X})\rightarrow \cdots \rightarrow \operatorname{cok}f_{p}^{X}).\nonumber\end{eqnarray}$$
 $[0\rightarrow \operatorname{cok}(f_{2}^{X}\cdots f_{p}^{X})\rightarrow \cdots \rightarrow \operatorname{cok}f_{p}^{X}]$
are epimorphisms.
$[0\rightarrow \operatorname{cok}(f_{2}^{X}\cdots f_{p}^{X})\rightarrow \cdots \rightarrow \operatorname{cok}f_{p}^{X}]$
are epimorphisms.
-
(ii) For the counit
 $\unicode[STIX]{x1D711}_{X}:\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70B}X\rightarrow X$
, we have
$\unicode[STIX]{x1D711}_{X}:\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70B}X\rightarrow X$
, we have  $$\begin{eqnarray}\displaystyle \ker \unicode[STIX]{x1D711}_{X} & = & \displaystyle \unicode[STIX]{x1D704}(0\rightarrow \ker f_{1}^{X}\rightarrow \cdots \rightarrow \ker (f_{1}^{X}\cdots f_{p-1}^{X}))\qquad \text{and}\nonumber\\ \displaystyle \operatorname{cok}\unicode[STIX]{x1D711}_{X} & = & \displaystyle \unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}X.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ker \unicode[STIX]{x1D711}_{X} & = & \displaystyle \unicode[STIX]{x1D704}(0\rightarrow \ker f_{1}^{X}\rightarrow \cdots \rightarrow \ker (f_{1}^{X}\cdots f_{p-1}^{X}))\qquad \text{and}\nonumber\\ \displaystyle \operatorname{cok}\unicode[STIX]{x1D711}_{X} & = & \displaystyle \unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}X.\nonumber\end{eqnarray}$$
We first study extensions in
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, where the first term is in the image of the functor
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, where the first term is in the image of the functor
![]() $\unicode[STIX]{x1D704}$
.
$\unicode[STIX]{x1D704}$
.
Lemma 5.3. Let
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D702}$
be as in Section 3. For
$\unicode[STIX]{x1D702}$
be as in Section 3. For
![]() $X\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
and
$X\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
and
![]() $Y\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, we have
$Y\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, we have
If, moreover, all of the maps
![]() $f_{2}^{Y},\ldots ,f_{p}^{Y}$
are epimorphisms, then the equality also holds for
$f_{2}^{Y},\ldots ,f_{p}^{Y}$
are epimorphisms, then the equality also holds for
![]() $n=\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
.
$n=\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
.
Proof. We first observe that
so the
![]() $\operatorname{Ext}$
space of the lemma vanishes provided that
$\operatorname{Ext}$
space of the lemma vanishes provided that
-
(1)
 $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D704}X,\ker \unicode[STIX]{x1D700}_{Y})=0$
and
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D704}X,\ker \unicode[STIX]{x1D700}_{Y})=0$
and -
(2)
 $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n-1}(\unicode[STIX]{x1D704}X,\operatorname{cok}\unicode[STIX]{x1D700}_{Y})=0$
.
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n-1}(\unicode[STIX]{x1D704}X,\operatorname{cok}\unicode[STIX]{x1D700}_{Y})=0$
.
For the first space, we use Observation 5.2 to simplify
so this space vanishes provided that
![]() $n>\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
, and hence by Lemma 5.1 for
$n>\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}[\!\sqrt[p-1]{0}]$
, and hence by Lemma 5.1 for
![]() $n>\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
. Moreover, using the second part of Lemma 5.1, we see that this bound may be improved by
$n>\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
. Moreover, using the second part of Lemma 5.1, we see that this bound may be improved by
![]() $1$
provided that all of the maps
$1$
provided that all of the maps
![]() $f_{2}^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}Y},\ldots f_{p-1}^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}Y}$
are epimorphisms. This holds provided that the corresponding maps
$f_{2}^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}Y},\ldots f_{p-1}^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}Y}$
are epimorphisms. This holds provided that the corresponding maps
![]() $f_{2}^{Y},\ldots ,f_{p-1}^{Y}$
are epi.
$f_{2}^{Y},\ldots ,f_{p-1}^{Y}$
are epi.
For the second space, we use the remark in the first point of Observation 5.2. Note that this precisely tells us that we are in the situation of the second point of Lemma 5.1, whence
Finally, we note that if all of the maps
![]() $f_{2}^{Y},\ldots ,f_{p}^{Y}$
are epi, then
$f_{2}^{Y},\ldots ,f_{p}^{Y}$
are epi, then
![]() $\operatorname{cok}\unicode[STIX]{x1D700}_{Y}=0$
, so the space in the second point vanishes.◻
$\operatorname{cok}\unicode[STIX]{x1D700}_{Y}=0$
, so the space in the second point vanishes.◻
In the next step, we assume that the first object lies in the set
![]() ${\mathcal{E}}$
, that is, that the map
${\mathcal{E}}$
, that is, that the map
![]() $f_{1}^{X}\cdots f_{p-1}^{X}$
is a monomorphism.
$f_{1}^{X}\cdots f_{p-1}^{X}$
is a monomorphism.
Lemma 5.4. Let
![]() $X\in {\mathcal{E}}$
and
$X\in {\mathcal{E}}$
and
![]() $Y\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Then,
$Y\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. Then,
If, moreover, all of the maps
![]() $f_{2}^{Y},\ldots ,f_{p}^{Y}$
are epimorphisms, then
$f_{2}^{Y},\ldots ,f_{p}^{Y}$
are epimorphisms, then
Proof. We start by observing that
![]() $X\in {\mathcal{E}}$
is equivalent to
$X\in {\mathcal{E}}$
is equivalent to
![]() $\ker \unicode[STIX]{x1D711}_{X}=0$
, whence we have the short exact sequence
$\ker \unicode[STIX]{x1D711}_{X}=0$
, whence we have the short exact sequence
Therefore, it suffices to consider the two
![]() $\operatorname{Ext}$
spaces
$\operatorname{Ext}$
spaces
![]() $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70B}X,Y)$
and
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70B}X,Y)$
and
![]() $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}X,Y)$
.
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}X,Y)$
.
For the first of these, we note that
so this vanishes for
![]() $n>\operatorname{gldim}{\mathcal{A}}$
.
$n>\operatorname{gldim}{\mathcal{A}}$
.
For the second one, we use Lemma 5.3 above. ◻
Remark 5.5. We observe that we have now completed an inductive proof of the upper bounds in Lemma 5.1. In fact, in the case
![]() $F=0$
we have
$F=0$
we have
![]() ${\mathcal{E}}={\mathcal{A}}[\!\sqrt[p]{0}]$
, so there is no restriction on
${\mathcal{E}}={\mathcal{A}}[\!\sqrt[p]{0}]$
, so there is no restriction on
![]() $X$
in the lemma above. The equality claimed in parenthesis in Lemma 5.1 follows from the following result.
$X$
in the lemma above. The equality claimed in parenthesis in Lemma 5.1 follows from the following result.
Lemma 5.6. Let
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D702}$
be as in Section 3, and let
$\unicode[STIX]{x1D702}$
be as in Section 3, and let
![]() $p\geqslant 2$
. Then,
$p\geqslant 2$
. Then,
Proof. We have
![]() $\operatorname{gldim}{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]\geqslant \operatorname{gldim}{\mathcal{A}}$
because, for
$\operatorname{gldim}{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]\geqslant \operatorname{gldim}{\mathcal{A}}$
because, for
![]() $X,Y\in {\mathcal{A}}$
,
$X,Y\in {\mathcal{A}}$
,
To see that
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]\geqslant \operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
, we recall that for
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]\geqslant \operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1$
, we recall that for
![]() $Y\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}$
, we have
$Y\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}$
, we have
Now, we observe that we have an epimorphism
![]() $f:\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}Y\rightarrow \unicode[STIX]{x1D704}\unicode[STIX]{x1D6E5}Y$
in the category
$f:\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}Y\rightarrow \unicode[STIX]{x1D704}\unicode[STIX]{x1D6E5}Y$
in the category
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. We may explicitly describe the kernel of
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. We may explicitly describe the kernel of
![]() $f$
as
$f$
as
For any
![]() $X\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}$
, we have
$X\in {\mathcal{A}}_{\unicode[STIX]{x1D702}}$
, we have
![]() $\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D704}\unicode[STIX]{x1D6E5}X,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}Y)=\operatorname{Ext}_{{\mathcal{A}}}^{n}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D704}\unicode[STIX]{x1D6E5}X,Y)=0$
. Thus, the short exact sequence
$\operatorname{Ext}_{{\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]}^{n}(\unicode[STIX]{x1D704}\unicode[STIX]{x1D6E5}X,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}Y)=\operatorname{Ext}_{{\mathcal{A}}}^{n}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D704}\unicode[STIX]{x1D6E5}X,Y)=0$
. Thus, the short exact sequence
gives rise to isomorphisms
for all
![]() $n$
. It follows that
$n$
. It follows that
We are now ready to prove the main result of this section, giving the precise value of the global dimension of the category
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
under the assumption that
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
under the assumption that
![]() $F$
is an equivalence.
$F$
is an equivalence.
Theorem 5.7. Let
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D702}$
be as in Section 3, and assume additionally that
$\unicode[STIX]{x1D702}$
be as in Section 3, and assume additionally that
![]() $F$
is an equivalence. Then,
$F$
is an equivalence. Then,
One key ingredient for the proof is the following observation.
Observation 5.8. The functor
![]() $F$
induces an endofunctor
$F$
induces an endofunctor
![]() $\sqrt[p]{F}$
of
$\sqrt[p]{F}$
of
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, given by
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, given by
Moreover, if
![]() $F$
is an autoequivalence of
$F$
is an autoequivalence of
![]() ${\mathcal{A}}$
, then
${\mathcal{A}}$
, then
![]() $\sqrt[p]{F}$
is an autoequivalence of
$\sqrt[p]{F}$
is an autoequivalence of
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
.
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
.
Proof. For
![]() $X\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, we consider the short exact sequence
$X\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
, we consider the short exact sequence
We may explicitly describe the rightmost term by
and, in particular, all of the maps
![]() $f_{2}^{\operatorname{im}\unicode[STIX]{x1D700}_{X}},\ldots f_{p}^{\operatorname{im}\unicode[STIX]{x1D700}_{X}}$
are monomorphisms. It follows that
$f_{2}^{\operatorname{im}\unicode[STIX]{x1D700}_{X}},\ldots f_{p}^{\operatorname{im}\unicode[STIX]{x1D700}_{X}}$
are monomorphisms. It follows that
It follows that, for all
![]() $Y\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
,
$Y\in {\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
,
for
![]() $n>\max \{\operatorname{gldim}{\mathcal{A}},\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1\}$
. (The first equality holds because
$n>\max \{\operatorname{gldim}{\mathcal{A}},\operatorname{gldim}{\mathcal{A}}_{\unicode[STIX]{x1D702}}+1\}$
. (The first equality holds because
![]() $\sqrt[p]{F}$
is an autoequivalence; the second is Lemma 5.4.)
$\sqrt[p]{F}$
is an autoequivalence; the second is Lemma 5.4.)
On the other hand, since
![]() $\ker \unicode[STIX]{x1D700}_{X}=\unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}X$
, we also have that
$\ker \unicode[STIX]{x1D700}_{X}=\unicode[STIX]{x1D704}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D70C}}X$
, we also have that
by Lemma 5.3.
Now, note that
![]() $X$
is the middle term of a short exact sequence with
$X$
is the middle term of a short exact sequence with
![]() $\ker \unicode[STIX]{x1D700}_{X}$
and
$\ker \unicode[STIX]{x1D700}_{X}$
and
![]() $\operatorname{im}\unicode[STIX]{x1D700}_{X}$
as end terms. Therefore, we have
$\operatorname{im}\unicode[STIX]{x1D700}_{X}$
as end terms. Therefore, we have
This is the desired upper bound for the global dimension of
![]() ${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. The fact that this is also a lower bound is seen in Lemma 5.6 above.◻
${\mathcal{A}}[\!\sqrt[p]{\unicode[STIX]{x1D702}}]$
. The fact that this is also a lower bound is seen in Lemma 5.6 above.◻
Remark 5.9. In the case that
![]() $F$
is not an equivalence, one may extend the argument in the proof of Lemma 5.4 to the case where
$F$
is not an equivalence, one may extend the argument in the proof of Lemma 5.4 to the case where
![]() $X$
is not necessarily in
$X$
is not necessarily in
![]() ${\mathcal{E}}$
. In that case one has to account for a possible kernel of
${\mathcal{E}}$
. In that case one has to account for a possible kernel of
![]() $\unicode[STIX]{x1D711}_{X}$
, resulting in the weaker upper bound
$\unicode[STIX]{x1D711}_{X}$
, resulting in the weaker upper bound
However, we do not have any examples of Theorem 5.7 failing when
![]() $F$
is not an equivalence.
$F$
is not an equivalence.
Finally, we may apply Theorem 5.7 repeatedly to obtain the global dimension of categories of the form
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
.
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
.
Corollary 5.10. In the general situation of Theorem 4.7, and assuming further that all of the
![]() $F_{i}$
are autoequivalences, we have
$F_{i}$
are autoequivalences, we have
(Here we set
![]() $\operatorname{gldim}0=-\infty$
, or alternatively let the maximum run over all
$\operatorname{gldim}0=-\infty$
, or alternatively let the maximum run over all
![]() $I$
such that
$I$
such that
![]() ${\mathcal{A}}_{I}\neq 0$
.)
${\mathcal{A}}_{I}\neq 0$
.)
Proof. We can construct the category
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
iteratively, using the fact that
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
iteratively, using the fact that
where we have extended the action of
![]() $F_{i+1}$
to
$F_{i+1}$
to
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\sqrt[p_{i}]{\unicode[STIX]{x1D702}_{i}}]$
component wise. Since the
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\sqrt[p_{i}]{\unicode[STIX]{x1D702}_{i}}]$
component wise. Since the
![]() $F_{i}$
commute, this construction is well defined and equals our original construction. Thus, the result follows from Theorem 5.7 applied repeatedly.◻
$F_{i}$
commute, this construction is well defined and equals our original construction. Thus, the result follows from Theorem 5.7 applied repeatedly.◻
6 Applications to orders on projective varieties
In [Reference Iyama and LernerIL], GL orders on
![]() $\mathbb{P}^{d}$
were used to study GL weighted projective spaces, which in turn were introduced in [Reference Herschend, Iyama, Minamoto and OppermannHIMO]. We have already introduced GL orders in Definition 1.1: they are orders made up of tensor products of sheaves of algebras of the form
$\mathbb{P}^{d}$
were used to study GL weighted projective spaces, which in turn were introduced in [Reference Herschend, Iyama, Minamoto and OppermannHIMO]. We have already introduced GL orders in Definition 1.1: they are orders made up of tensor products of sheaves of algebras of the form
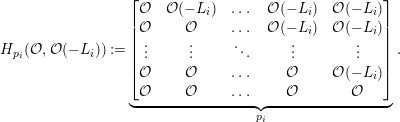 $$\begin{eqnarray}H_{p_{i}}({\mathcal{O}},{\mathcal{O}}(-L_{i})):=\underbrace{\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]}_{p_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{p_{i}}({\mathcal{O}},{\mathcal{O}}(-L_{i})):=\underbrace{\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}}(-L_{i}) & {\mathcal{O}}(-L_{i})\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]}_{p_{i}}.\end{eqnarray}$$
The connection that the category
![]() ${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
has to orders is described in the following proposition.
${\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
has to orders is described in the following proposition.
Proposition 6.1. Let
![]() $X$
be a projective variety over
$X$
be a projective variety over
![]() $k$
, and let
$k$
, and let
![]() $L_{1},\ldots ,L_{n}$
be effective Cartier divisors on
$L_{1},\ldots ,L_{n}$
be effective Cartier divisors on
![]() $X$
. Let
$X$
. Let
![]() ${\mathcal{A}}=\mathsf{coh}\,X$
,
${\mathcal{A}}=\mathsf{coh}\,X$
,
![]() $F_{i}:=-\otimes _{X}{\mathcal{O}}(-L_{i})$
and
$F_{i}:=-\otimes _{X}{\mathcal{O}}(-L_{i})$
and
![]() $\unicode[STIX]{x1D702}_{i}$
be given by tensoring with the natural inclusion
$\unicode[STIX]{x1D702}_{i}$
be given by tensoring with the natural inclusion
![]() ${\mathcal{O}}(-L_{i}){\hookrightarrow}{\mathcal{O}}$
. If
${\mathcal{O}}(-L_{i}){\hookrightarrow}{\mathcal{O}}$
. If
then
Proof. Let
![]() $e_{i}\in H^{0}(X,A_{j})$
be the global section with a
$e_{i}\in H^{0}(X,A_{j})$
be the global section with a
![]() $1$
in the
$1$
in the
![]() $(i,i)$
-entry and
$(i,i)$
-entry and
![]() $0$
elsewhere.
$0$
elsewhere.
We define the function
![]() $\unicode[STIX]{x1D6F7}:\mathsf{mod}\,A\rightarrow {\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
as follows. For
$\unicode[STIX]{x1D6F7}:\mathsf{mod}\,A\rightarrow {\mathcal{A}}[\!\sqrt[p_{1}]{\unicode[STIX]{x1D702}_{1}},\ldots ,\!\sqrt[p_{n}]{\unicode[STIX]{x1D702}_{n}}]$
as follows. For
![]() $M\in \mathsf{mod}\,A$
and
$M\in \mathsf{mod}\,A$
and
![]() $\mathbf{a}\in S=\{1,\ldots ,p_{1}\}\times \cdots \times \{1,\ldots ,p_{n}\}$
, set
$\mathbf{a}\in S=\{1,\ldots ,p_{1}\}\times \cdots \times \{1,\ldots ,p_{n}\}$
, set
As before, we extend this to allow the components of
![]() $\mathbf{a}$
to be
$\mathbf{a}$
to be
![]() $0$
, and treat them as functors
$0$
, and treat them as functors
![]() $F_{i}$
; that is,
$F_{i}$
; that is,
![]() $M_{\mathbf{a}}:=F_{i}M_{\mathbf{a}+p_{i}\mathbf{e}_{i}}$
, if
$M_{\mathbf{a}}:=F_{i}M_{\mathbf{a}+p_{i}\mathbf{e}_{i}}$
, if
![]() $a_{i}=0$
.
$a_{i}=0$
.
Now, set
to be the natural map coming from the
![]() $A_{i}$
-module structure.◻
$A_{i}$
-module structure.◻
From now on, we assume the following.
Assumption 6.2.
![]() $X$
is smooth and
$X$
is smooth and
![]() $D=\sum L_{i}$
is a simple normal crossing divisor; that is, for all
$D=\sum L_{i}$
is a simple normal crossing divisor; that is, for all
![]() $x\in \text{Supp}\,D$
, the local equations of
$x\in \text{Supp}\,D$
, the local equations of
![]() $L_{i}$
form a regular sequence in
$L_{i}$
form a regular sequence in
![]() ${\mathcal{O}}_{X,x}$
.
${\mathcal{O}}_{X,x}$
.
Proposition 6.3. The global dimension of
![]() $A$
is equal to the dimension of
$A$
is equal to the dimension of
![]() $X$
(and, in particular, finite).
$X$
(and, in particular, finite).
Proof. Let
![]() $d=\dim X$
. The assumption on the
$d=\dim X$
. The assumption on the
![]() $L_{i}$
implies that the intersections
$L_{i}$
implies that the intersections
![]() $\cap _{i\in I}L_{i}$
are smooth of dimension
$\cap _{i\in I}L_{i}$
are smooth of dimension
![]() $d-|I|$
, or empty. Thus, we have
$d-|I|$
, or empty. Thus, we have
The claim now follows from Corollary 5.10.
Alternatively, one may observe that the proof for the case
![]() $X=\mathbb{P}^{d}$
in [Reference Iyama and LernerIL, Proposition 2.13] generalizes immediately to an arbitrary smooth
$X=\mathbb{P}^{d}$
in [Reference Iyama and LernerIL, Proposition 2.13] generalizes immediately to an arbitrary smooth
![]() $X$
and
$X$
and
![]() $L_{i}$
.◻
$L_{i}$
.◻
Corollary 6.4. ([Reference Iyama and LernerIL], Proposition 5.2)
Let
![]() $T$
be a tilting object in
$T$
be a tilting object in
![]() $\mathsf{mod}\,A$
.
$\mathsf{mod}\,A$
.
-
∙
 $\mathsf{D}^{\operatorname{b}}(\mathsf{mod}\,A)=\mathsf{thick}\,T$
.
$\mathsf{D}^{\operatorname{b}}(\mathsf{mod}\,A)=\mathsf{thick}\,T$
. -
∙ There is a triangle equivalence
 $\mathsf{D}^{\operatorname{b}}(\mathsf{mod}\,A)\simeq \mathsf{D}^{\operatorname{b}}(\mathsf{mod}\,\operatorname{End}_{A}(T))$
.
$\mathsf{D}^{\operatorname{b}}(\mathsf{mod}\,A)\simeq \mathsf{D}^{\operatorname{b}}(\mathsf{mod}\,\operatorname{End}_{A}(T))$
.
Proposition 6.5. (Serre duality)
Let
![]() $A$
be a GL order, as before, and put
$A$
be a GL order, as before, and put
![]() $d=\text{dim}\,X$
. Let
$d=\text{dim}\,X$
. Let
which is an
![]() $A$
-bimodule. Then, for any
$A$
-bimodule. Then, for any
![]() $M,N\in \mathsf{mod}\,A$
, we have
$M,N\in \mathsf{mod}\,A$
, we have
where
![]() $D(-)=\operatorname{Hom}_{k}(-,k)$
.
$D(-)=\operatorname{Hom}_{k}(-,k)$
.
Proof. This proof is adapted from [Reference Artin and de JongAdJ]. Let
![]() $h^{i}:\mathsf{D}^{b}(\mathsf{mod}\,A)\rightarrow \mathsf{mod}\,A$
be the
$h^{i}:\mathsf{D}^{b}(\mathsf{mod}\,A)\rightarrow \mathsf{mod}\,A$
be the
![]() $i$
th cohomology functor, let
$i$
th cohomology functor, let
![]() $\mathbf{R}\unicode[STIX]{x1D6E4}$
be the right derived functor of the global sections functor
$\mathbf{R}\unicode[STIX]{x1D6E4}$
be the right derived functor of the global sections functor
![]() $\unicode[STIX]{x1D6E4}$
, let
$\unicode[STIX]{x1D6E4}$
, let
![]() $\mathbf{R}{\mathcal{H}}om_{A}(-,N)$
be the right derived functor of the sheaf hom functor
$\mathbf{R}{\mathcal{H}}om_{A}(-,N)$
be the right derived functor of the sheaf hom functor
![]() ${\mathcal{H}}om_{A}(-,N)$
, and let
${\mathcal{H}}om_{A}(-,N)$
, and let
![]() $-\otimes _{A}^{\mathbf{L}}N$
be the left derived functor of the tensor functor. For simplicity, we introduce some more notation. Let
$-\otimes _{A}^{\mathbf{L}}N$
be the left derived functor of the tensor functor. For simplicity, we introduce some more notation. Let
![]() $\mathbb{H}^{i}:=h^{i}\circ \mathbf{R}\unicode[STIX]{x1D6E4}$
be the hypercohomology functor, and for
$\mathbb{H}^{i}:=h^{i}\circ \mathbf{R}\unicode[STIX]{x1D6E4}$
be the hypercohomology functor, and for
![]() $M\in \mathsf{D}(\mathsf{mod}\,A)$
, let
$M\in \mathsf{D}(\mathsf{mod}\,A)$
, let
![]() $M^{\ast }:=\mathbf{R}{\mathcal{H}}om_{A}(M,A)$
. With this, we have
$M^{\ast }:=\mathbf{R}{\mathcal{H}}om_{A}(M,A)$
. With this, we have
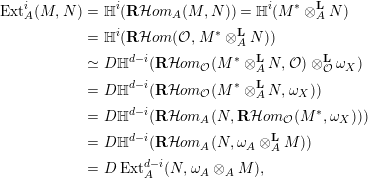 $$\begin{eqnarray}\displaystyle \operatorname{Ext}_{A}^{i}(M,N) & = & \displaystyle \mathbb{H}^{i}(\mathbf{R}{\mathcal{H}}om_{A}(M,N))=\mathbb{H}^{i}(M^{\ast }\otimes _{A}^{\mathbf{L}}N)\nonumber\\ \displaystyle & = & \displaystyle \mathbb{H}^{i}(\mathbf{R}{\mathcal{H}}om({\mathcal{O}},M^{\ast }\otimes _{A}^{\mathbf{L}}N))\nonumber\\ \displaystyle & \simeq & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{{\mathcal{O}}}(M^{\ast }\otimes _{A}^{\mathbf{L}}N,{\mathcal{O}})\otimes _{{\mathcal{O}}}^{\mathbf{L}}\unicode[STIX]{x1D714}_{X})\nonumber\\ \displaystyle & = & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{{\mathcal{O}}}(M^{\ast }\otimes _{A}^{\mathbf{L}}N,\unicode[STIX]{x1D714}_{X}))\nonumber\\ \displaystyle & = & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{A}(N,\mathbf{R}{\mathcal{H}}om_{{\mathcal{O}}}(M^{\ast },\unicode[STIX]{x1D714}_{X})))\nonumber\\ \displaystyle & = & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{A}(N,\unicode[STIX]{x1D714}_{A}\otimes _{A}^{\mathbf{L}}M))\nonumber\\ \displaystyle & = & \displaystyle D\operatorname{Ext}_{A}^{d-i}(N,\unicode[STIX]{x1D714}_{A}\otimes _{A}M),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ext}_{A}^{i}(M,N) & = & \displaystyle \mathbb{H}^{i}(\mathbf{R}{\mathcal{H}}om_{A}(M,N))=\mathbb{H}^{i}(M^{\ast }\otimes _{A}^{\mathbf{L}}N)\nonumber\\ \displaystyle & = & \displaystyle \mathbb{H}^{i}(\mathbf{R}{\mathcal{H}}om({\mathcal{O}},M^{\ast }\otimes _{A}^{\mathbf{L}}N))\nonumber\\ \displaystyle & \simeq & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{{\mathcal{O}}}(M^{\ast }\otimes _{A}^{\mathbf{L}}N,{\mathcal{O}})\otimes _{{\mathcal{O}}}^{\mathbf{L}}\unicode[STIX]{x1D714}_{X})\nonumber\\ \displaystyle & = & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{{\mathcal{O}}}(M^{\ast }\otimes _{A}^{\mathbf{L}}N,\unicode[STIX]{x1D714}_{X}))\nonumber\\ \displaystyle & = & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{A}(N,\mathbf{R}{\mathcal{H}}om_{{\mathcal{O}}}(M^{\ast },\unicode[STIX]{x1D714}_{X})))\nonumber\\ \displaystyle & = & \displaystyle D\mathbb{H}^{d-i}(\mathbf{R}{\mathcal{H}}om_{A}(N,\unicode[STIX]{x1D714}_{A}\otimes _{A}^{\mathbf{L}}M))\nonumber\\ \displaystyle & = & \displaystyle D\operatorname{Ext}_{A}^{d-i}(N,\unicode[STIX]{x1D714}_{A}\otimes _{A}M),\nonumber\end{eqnarray}$$
and we are done. ◻
Corollary 6.6.
![]() $T\in \mathsf{mod}\,A$
is tilting if and only if it is cotilting.
$T\in \mathsf{mod}\,A$
is tilting if and only if it is cotilting.
Proof. The proof follows immediately from 6.5. ◻
We now translate our results from Sections 3 and 4 to the category
![]() $\mathsf{mod}\,A$
, but in light of the previous result we will say that
$\mathsf{mod}\,A$
, but in light of the previous result we will say that
![]() $T$
is tilting, as opposed to cotilting.
$T$
is tilting, as opposed to cotilting.
First, for each
![]() $i=1,\ldots ,n$
, we consider a sheafified version of the standard recollement we presented in Example 3.6. It follows immediately from the explicit description of
$i=1,\ldots ,n$
, we consider a sheafified version of the standard recollement we presented in Example 3.6. It follows immediately from the explicit description of
![]() $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
![]() $\unicode[STIX]{x1D70B}$
that this recollement coincides, via the equivalence of Proposition 6.1, with the recollement of Proposition 3.7.
$\unicode[STIX]{x1D70B}$
that this recollement coincides, via the equivalence of Proposition 6.1, with the recollement of Proposition 3.7.
Let
![]() $e_{i}$
be the global idempotent of
$e_{i}$
be the global idempotent of
![]() $A_{i}$
with
$A_{i}$
with
![]() $1$
in the bottom right entry and
$1$
in the bottom right entry and
![]() $0$
elsewhere. We have the recollement
$0$
elsewhere. We have the recollement
where the terms explicitly are
 $$\begin{eqnarray}\displaystyle \frac{A_{i}}{\langle e_{i}\rangle } & = & \displaystyle \underbrace{\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}}_{L_{i}} & 0 & \ldots \, & \ldots \, & 0\\ {\mathcal{O}}_{L_{i}} & {\mathcal{O}}_{L_{i}} & 0 & \ldots \, & 0\\ \vdots & \vdots & & & \vdots \\ {\mathcal{O}}_{L_{i}} & {\mathcal{O}}_{L_{i}} & \ldots \, & \ldots \, & {\mathcal{O}}_{L_{i}}\end{array}\right]}_{p_{i}-1},\nonumber\\ \displaystyle A_{i} & = & \displaystyle \underbrace{\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & \ldots \, & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & {\mathcal{O}}(-L_{i})\\ \vdots & \vdots & & & \vdots \\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & \ldots \, & {\mathcal{O}}\end{array}\right]}_{p_{i}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{and}\quad \mathsf{mod}\,e_{i}A_{i}e_{i}=\mathsf{coh}\,X.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{A_{i}}{\langle e_{i}\rangle } & = & \displaystyle \underbrace{\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}}_{L_{i}} & 0 & \ldots \, & \ldots \, & 0\\ {\mathcal{O}}_{L_{i}} & {\mathcal{O}}_{L_{i}} & 0 & \ldots \, & 0\\ \vdots & \vdots & & & \vdots \\ {\mathcal{O}}_{L_{i}} & {\mathcal{O}}_{L_{i}} & \ldots \, & \ldots \, & {\mathcal{O}}_{L_{i}}\end{array}\right]}_{p_{i}-1},\nonumber\\ \displaystyle A_{i} & = & \displaystyle \underbrace{\left[\begin{array}{@{}ccccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & \ldots \, & {\mathcal{O}}(-L_{i})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}(-L_{i}) & \ldots \, & {\mathcal{O}}(-L_{i})\\ \vdots & \vdots & & & \vdots \\ {\mathcal{O}} & {\mathcal{O}} & \ldots \, & \ldots \, & {\mathcal{O}}\end{array}\right]}_{p_{i}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{and}\quad \mathsf{mod}\,e_{i}A_{i}e_{i}=\mathsf{coh}\,X.\nonumber\end{eqnarray}$$
Here, the functor
![]() $\unicode[STIX]{x1D704}$
is natural inclusion, and
$\unicode[STIX]{x1D704}$
is natural inclusion, and
![]() $\unicode[STIX]{x1D70B}$
is given by
$\unicode[STIX]{x1D70B}$
is given by
![]() $\unicode[STIX]{x1D70B}(N)=e_{i}N$
. In particular,
$\unicode[STIX]{x1D70B}(N)=e_{i}N$
. In particular,
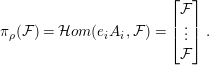 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}({\mathcal{F}})={\mathcal{H}}om(e_{i}A_{i},{\mathcal{F}})=\left[\begin{array}{@{}c@{}}{\mathcal{F}}\\ \vdots \\ {\mathcal{F}}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70C}}({\mathcal{F}})={\mathcal{H}}om(e_{i}A_{i},{\mathcal{F}})=\left[\begin{array}{@{}c@{}}{\mathcal{F}}\\ \vdots \\ {\mathcal{F}}\end{array}\right].\end{eqnarray}$$
Furthermore, if
![]() $T$
is a tilting object in
$T$
is a tilting object in
![]() $\mathsf{coh}\,L_{i}$
, then the tilting object
$\mathsf{coh}\,L_{i}$
, then the tilting object
![]() $\unicode[STIX]{x1D6FF}(T)$
in
$\unicode[STIX]{x1D6FF}(T)$
in
![]() $\mathsf{mod}\frac{A_{i}}{\langle e_{i}\rangle }$
is given by
$\mathsf{mod}\frac{A_{i}}{\langle e_{i}\rangle }$
is given by
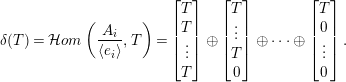 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}(T)={\mathcal{H}}om\left(\frac{A_{i}}{\langle e_{i}\rangle },T\right)=\left[\begin{array}{@{}c@{}}T\\ T\\ \vdots \\ T\end{array}\right]\oplus \left[\begin{array}{@{}c@{}}T\\ \vdots \\ T\\ 0\end{array}\right]\oplus \cdots \oplus \left[\begin{array}{@{}c@{}}T\\ 0\\ \vdots \\ 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}(T)={\mathcal{H}}om\left(\frac{A_{i}}{\langle e_{i}\rangle },T\right)=\left[\begin{array}{@{}c@{}}T\\ T\\ \vdots \\ T\end{array}\right]\oplus \left[\begin{array}{@{}c@{}}T\\ \vdots \\ T\\ 0\end{array}\right]\oplus \cdots \oplus \left[\begin{array}{@{}c@{}}T\\ 0\\ \vdots \\ 0\end{array}\right].\end{eqnarray}$$
(To see this, compare the definition of
![]() $\unicode[STIX]{x1D6FF}$
at the beginning of Section 3 with the equivalence of Proposition 6.1.)
$\unicode[STIX]{x1D6FF}$
at the beginning of Section 3 with the equivalence of Proposition 6.1.)
As a final step for translating our general setup from Section 4 to the explicit setup here, note that the restriction functors are just given by tensoring with the structure sheaf on the corresponding subvarieties. Thus, writing
![]() ${\mathcal{O}}_{J}$
for the structure sheaf on the intersection
${\mathcal{O}}_{J}$
for the structure sheaf on the intersection
![]() $\cap _{c\in J}L_{j}$
, we obtain the following result directly by translating Theorem 4.7 to this setup.
$\cap _{c\in J}L_{j}$
, we obtain the following result directly by translating Theorem 4.7 to this setup.
Theorem 6.7. Let
![]() ${\mathcal{A}}=\mathsf{mod}\,A$
be as above. If, for all
${\mathcal{A}}=\mathsf{mod}\,A$
be as above. If, for all
![]() $I,J\subseteq \{1,\ldots ,n\}$
with
$I,J\subseteq \{1,\ldots ,n\}$
with
![]() $I\cap J=\emptyset$
and
$I\cap J=\emptyset$
and
![]() $j\not \in I\cup J$
,
$j\not \in I\cup J$
,
-
∙
 $T_{I}\otimes {\mathcal{O}}_{J}\otimes {\mathcal{O}}(-L_{j})\rightarrow T_{I}\otimes {\mathcal{O}}_{J}$
is injective,
$T_{I}\otimes {\mathcal{O}}_{J}\otimes {\mathcal{O}}(-L_{j})\rightarrow T_{I}\otimes {\mathcal{O}}_{J}$
is injective, -
∙
 $\operatorname{Ext}_{{\mathcal{O}}_{I\cup J}}^{i}(T_{I}\otimes {\mathcal{O}}_{J},T_{I\cup J})=0$
, for all
$\operatorname{Ext}_{{\mathcal{O}}_{I\cup J}}^{i}(T_{I}\otimes {\mathcal{O}}_{J},T_{I\cup J})=0$
, for all
 $i>0$
,
$i>0$
,
then
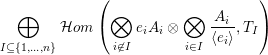 $$\begin{eqnarray}\bigoplus _{I\subseteq \{1,\ldots ,n\}}{\mathcal{H}}om\left(\mathop{\bigotimes }_{i\not \in I}e_{i}A_{i}\otimes \bigotimes _{i\in I}\frac{A_{i}}{\langle e_{i}\rangle },T_{I}\right)\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{I\subseteq \{1,\ldots ,n\}}{\mathcal{H}}om\left(\mathop{\bigotimes }_{i\not \in I}e_{i}A_{i}\otimes \bigotimes _{i\in I}\frac{A_{i}}{\langle e_{i}\rangle },T_{I}\right)\end{eqnarray}$$
is tilting in
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
7 Examples
We now apply Theorem 6.7 to various situations. Note that if
![]() $T_{I}$
is in fact a tilting bundle, then the first condition of the theorem is automatically satisfied. Furthermore, by Serre vanishing, we can always twist the
$T_{I}$
is in fact a tilting bundle, then the first condition of the theorem is automatically satisfied. Furthermore, by Serre vanishing, we can always twist the
![]() $T_{I}$
so that the second condition is also satisfied. Inertly, assuming that all
$T_{I}$
so that the second condition is also satisfied. Inertly, assuming that all
![]() $T_{I}$
with smaller index sets are already fixed, we twist
$T_{I}$
with smaller index sets are already fixed, we twist
![]() $T_{I\cup J}$
in the second condition by a sufficiently high power of
$T_{I\cup J}$
in the second condition by a sufficiently high power of
![]() ${\mathcal{O}}_{I\cup J}(1)$
to guarantee the
${\mathcal{O}}_{I\cup J}(1)$
to guarantee the
![]() $\operatorname{Ext}$
-vanishing in that condition.
$\operatorname{Ext}$
-vanishing in that condition.
7.1 Geigle–Lenzing weighted projective lines
Let
![]() $X=\mathbb{P}_{X_{0}:X_{1}}^{1}$
, and let
$X=\mathbb{P}_{X_{0}:X_{1}}^{1}$
, and let
![]() ${\mathcal{A}}=\mathsf{coh}\,X$
. For
${\mathcal{A}}=\mathsf{coh}\,X$
. For
![]() $i=1,\ldots ,n$
, choose points
$i=1,\ldots ,n$
, choose points
![]() $L_{i}=(\unicode[STIX]{x1D706}_{0,i}:\unicode[STIX]{x1D706}_{1,i})$
and corresponding weights
$L_{i}=(\unicode[STIX]{x1D706}_{0,i}:\unicode[STIX]{x1D706}_{1,i})$
and corresponding weights
![]() $p_{i}$
.
$p_{i}$
.
![]() $T_{\emptyset }={\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}(1)$
is a tilting object in
$T_{\emptyset }={\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}(1)$
is a tilting object in
![]() $\mathsf{coh}\,X$
and
$\mathsf{coh}\,X$
and
![]() $T_{\{i\}}={\mathcal{O}}_{L_{i}}$
is a tilting object in
$T_{\{i\}}={\mathcal{O}}_{L_{i}}$
is a tilting object in
![]() $\mathsf{coh}\,L_{i}$
. Then,
$\mathsf{coh}\,L_{i}$
. Then,
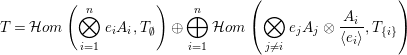 $$\begin{eqnarray}T={\mathcal{H}}om\left(\mathop{\bigotimes }_{i=1}^{n}e_{i}A_{i},T_{\emptyset }\right)\oplus \bigoplus _{i=1}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{j\neq i}e_{j}A_{j}\otimes \frac{A_{i}}{\langle e_{i}\rangle },T_{\{i\}}\right)\end{eqnarray}$$
$$\begin{eqnarray}T={\mathcal{H}}om\left(\mathop{\bigotimes }_{i=1}^{n}e_{i}A_{i},T_{\emptyset }\right)\oplus \bigoplus _{i=1}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{j\neq i}e_{j}A_{j}\otimes \frac{A_{i}}{\langle e_{i}\rangle },T_{\{i\}}\right)\end{eqnarray}$$
is a tilting object in
with endomorphism algebra
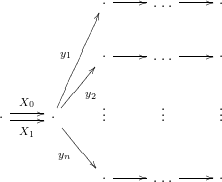
with relations
This algebra is known as the “squid”. (The reader may check directly that this is indeed the quiver with relations for the endomorphism algebra, or check our discussion of squid algebras more generally in Section 7.4.)
7.2 Geigle–Lenzing weighted
 $\mathbb{P}^{2}$
$\mathbb{P}^{2}$
Let
![]() ${\mathcal{A}}=\mathsf{coh}\,\mathbb{P}^{2}$
. Note that both lines and smooth conics in
${\mathcal{A}}=\mathsf{coh}\,\mathbb{P}^{2}$
. Note that both lines and smooth conics in
![]() $\mathbb{P}^{2}$
are isomorphic to
$\mathbb{P}^{2}$
are isomorphic to
![]() $\mathbb{P}^{1}$
, and hence have tilting bundles. Fix weights
$\mathbb{P}^{1}$
, and hence have tilting bundles. Fix weights
![]() $p_{1},\ldots ,p_{n}$
, and hyperplanes
$p_{1},\ldots ,p_{n}$
, and hyperplanes
![]() $L_{1},\ldots ,L_{l}$
, as well as smooth conics
$L_{1},\ldots ,L_{l}$
, as well as smooth conics
![]() $L_{l+1},\ldots ,L_{n}$
. As before, we consider the category
$L_{l+1},\ldots ,L_{n}$
. As before, we consider the category
![]() $T_{\emptyset }={\mathcal{O}}_{\mathbb{P}^{2}}(-2)\oplus {\mathcal{O}}_{\mathbb{P}^{2}}(-1)\oplus {\mathcal{O}}_{\mathbb{P}^{2}}$
is a tilting bundle in
$T_{\emptyset }={\mathcal{O}}_{\mathbb{P}^{2}}(-2)\oplus {\mathcal{O}}_{\mathbb{P}^{2}}(-1)\oplus {\mathcal{O}}_{\mathbb{P}^{2}}$
is a tilting bundle in
![]() $\mathsf{coh}\,\mathbb{P}^{2}$
,
$\mathsf{coh}\,\mathbb{P}^{2}$
,
![]() $T_{\{i\}}={\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)$
is a tilting bundle in
$T_{\{i\}}={\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)$
is a tilting bundle in
![]() $\mathsf{coh}\,L_{i}$
(where
$\mathsf{coh}\,L_{i}$
(where
![]() ${\mathcal{O}}_{L_{i}}(1)$
denotes the degree-
${\mathcal{O}}_{L_{i}}(1)$
denotes the degree-
![]() $1$
line bundle on
$1$
line bundle on
![]() $L_{i}$
), and
$L_{i}$
), and
![]() $T_{\{i,j\}}={\mathcal{O}}_{L_{i}\cap L_{j}}$
is a tilting bundle in
$T_{\{i,j\}}={\mathcal{O}}_{L_{i}\cap L_{j}}$
is a tilting bundle in
![]() $L_{i}\cap L_{j}$
. Thus, by Theorem 6.7,
$L_{i}\cap L_{j}$
. Thus, by Theorem 6.7,
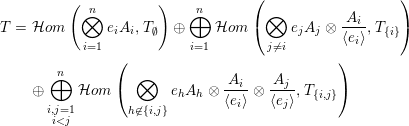 $$\begin{eqnarray}\displaystyle T & = & \displaystyle {\mathcal{H}}om\left(\mathop{\bigotimes }_{i=1}^{n}e_{i}A_{i},T_{\emptyset }\right)\oplus \bigoplus _{i=1}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{j\neq i}e_{j}A_{j}\otimes \frac{A_{i}}{\langle e_{i}\rangle },T_{\{i\}}\right)\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\substack{ i,j=1 \\ i<j}}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{h\not \in \{i,j\}}e_{h}A_{h}\otimes \frac{A_{i}}{\langle e_{i}\rangle }\otimes \frac{A_{j}}{\langle e_{j}\rangle },T_{\{i,j\}}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T & = & \displaystyle {\mathcal{H}}om\left(\mathop{\bigotimes }_{i=1}^{n}e_{i}A_{i},T_{\emptyset }\right)\oplus \bigoplus _{i=1}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{j\neq i}e_{j}A_{j}\otimes \frac{A_{i}}{\langle e_{i}\rangle },T_{\{i\}}\right)\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\substack{ i,j=1 \\ i<j}}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{h\not \in \{i,j\}}e_{h}A_{h}\otimes \frac{A_{i}}{\langle e_{i}\rangle }\otimes \frac{A_{j}}{\langle e_{j}\rangle },T_{\{i,j\}}\right)\nonumber\end{eqnarray}$$
is a tilting object provided that the two conditions of the theorem are satisfied. The first condition is automatically satisfied as all of the tilting objects are in fact vector bundles. Furthermore, the second condition is also satisfied as
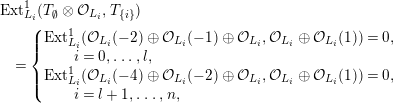 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Ext}_{L_{i}}^{1}(T_{\emptyset }\otimes {\mathcal{O}}_{L_{i}},T_{\{i\}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}l@{}}\operatorname{Ext}_{L_{i}}^{1}({\mathcal{O}}_{L_{i}}(-2)\oplus {\mathcal{O}}_{L_{i}}(-1)\oplus {\mathcal{O}}_{L_{i}},{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1))=0,\\ \qquad i=0,\ldots ,l,\\ \operatorname{Ext}_{L_{i}}^{1}({\mathcal{O}}_{L_{i}}(-4)\oplus {\mathcal{O}}_{L_{i}}(-2)\oplus {\mathcal{O}}_{L_{i}},{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1))=0,\\ \qquad i=l+1,\ldots ,n,\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Ext}_{L_{i}}^{1}(T_{\emptyset }\otimes {\mathcal{O}}_{L_{i}},T_{\{i\}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}l@{}}\operatorname{Ext}_{L_{i}}^{1}({\mathcal{O}}_{L_{i}}(-2)\oplus {\mathcal{O}}_{L_{i}}(-1)\oplus {\mathcal{O}}_{L_{i}},{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1))=0,\\ \qquad i=0,\ldots ,l,\\ \operatorname{Ext}_{L_{i}}^{1}({\mathcal{O}}_{L_{i}}(-4)\oplus {\mathcal{O}}_{L_{i}}(-2)\oplus {\mathcal{O}}_{L_{i}},{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1))=0,\\ \qquad i=l+1,\ldots ,n,\end{array}\right.\nonumber\end{eqnarray}$$
and so
![]() $T$
is indeed a tilting bundle in
$T$
is indeed a tilting bundle in
![]() $\mathsf{mod}\,A$
.
$\mathsf{mod}\,A$
.
7.3 Geigle–Lenzing weighted Hirzebruch surfaces
In this section, we follow King’s conventions from [Reference KingK]. For
![]() $m\geqslant 0$
, the Hirzebruch surface is defined as
$m\geqslant 0$
, the Hirzebruch surface is defined as
We embed such a surface in
![]() $\mathbb{P}_{x_{0}:x_{1}}^{1}\times \mathbb{P}_{y_{0}:\ldots :y_{m+1}}^{m+1}$
via
$\mathbb{P}_{x_{0}:x_{1}}^{1}\times \mathbb{P}_{y_{0}:\ldots :y_{m+1}}^{m+1}$
via
and so line bundles on
![]() $\unicode[STIX]{x1D6F4}_{m}$
arise as pullbacks of line bundles on
$\unicode[STIX]{x1D6F4}_{m}$
arise as pullbacks of line bundles on
![]() $\mathbb{P}^{1}$
and
$\mathbb{P}^{1}$
and
![]() $\mathbb{P}^{m+1}$
via the stated embedding followed by the natural projections. Thus,
$\mathbb{P}^{m+1}$
via the stated embedding followed by the natural projections. Thus,
![]() $\mathsf{Pic}\,\unicode[STIX]{x1D6F4}_{m}=\mathbb{Z}^{2}$
with intersection form
$\mathsf{Pic}\,\unicode[STIX]{x1D6F4}_{m}=\mathbb{Z}^{2}$
with intersection form
![]() $\left[\begin{array}{@{}cc@{}}0 & 1\\ 1 & m\end{array}\right]$
and canonical bundle
$\left[\begin{array}{@{}cc@{}}0 & 1\\ 1 & m\end{array}\right]$
and canonical bundle
![]() ${\mathcal{O}}(m-2,-2)$
. Using the adjunction formula, which states that a smooth genus
${\mathcal{O}}(m-2,-2)$
. Using the adjunction formula, which states that a smooth genus
![]() $g$
curve
$g$
curve
![]() $C$
on a surface
$C$
on a surface
![]() $X$
with canonical divisor
$X$
with canonical divisor
![]() $K$
satisfies
$K$
satisfies
we see that any curve of type
![]() $(a,1)$
or
$(a,1)$
or
![]() $(1,0)$
is rational and hence has a tilting bundle.
$(1,0)$
is rational and hence has a tilting bundle.
Until the end of this section, we let
![]() ${\mathcal{O}}={\mathcal{O}}_{\unicode[STIX]{x1D6F4}_{m}}$
. Similar to the GL weighted
${\mathcal{O}}={\mathcal{O}}_{\unicode[STIX]{x1D6F4}_{m}}$
. Similar to the GL weighted
![]() $\mathbb{P}^{2}$
case, for
$\mathbb{P}^{2}$
case, for
![]() $i=1,\ldots ,l$
let
$i=1,\ldots ,l$
let
![]() $L_{i}$
be a curve of type
$L_{i}$
be a curve of type
![]() $(a_{i},1)$
and for
$(a_{i},1)$
and for
![]() $i=l+1,\ldots ,n$
a
$i=l+1,\ldots ,n$
a
![]() $(1,0)$
divisor. Note that since
$(1,0)$
divisor. Note that since
![]() $L_{i}$
is effective,
$L_{i}$
is effective,
![]() $a_{i}\geqslant -m$
(see [Reference KingK, Proposition 6.1]). As before, we consider the category
$a_{i}\geqslant -m$
(see [Reference KingK, Proposition 6.1]). As before, we consider the category
Let
![]() $T_{\emptyset }={\mathcal{O}}\oplus {\mathcal{O}}(1,0)\oplus {\mathcal{O}}(0,1)\oplus {\mathcal{O}}(1,1)$
, which is a tilting bundle in
$T_{\emptyset }={\mathcal{O}}\oplus {\mathcal{O}}(1,0)\oplus {\mathcal{O}}(0,1)\oplus {\mathcal{O}}(1,1)$
, which is a tilting bundle in
![]() $\mathsf{coh}\,\unicode[STIX]{x1D6F4}_{m}$
. For
$\mathsf{coh}\,\unicode[STIX]{x1D6F4}_{m}$
. For
![]() $i=1,\ldots ,l$
, let
$i=1,\ldots ,l$
, let
![]() $T_{\{i\}}={\mathcal{O}}_{L_{i}}(a_{i}+m)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m+1)$
, and let
$T_{\{i\}}={\mathcal{O}}_{L_{i}}(a_{i}+m)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m+1)$
, and let
![]() $T_{\{i\}}={\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)$
for
$T_{\{i\}}={\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)$
for
![]() $i=l+1,\ldots ,m$
. Finally, let
$i=l+1,\ldots ,m$
. Finally, let
![]() $T_{\{i,j\}}={\mathcal{O}}_{L_{i}\cap L_{j}}$
. Thus, by Theorem 6.7,
$T_{\{i,j\}}={\mathcal{O}}_{L_{i}\cap L_{j}}$
. Thus, by Theorem 6.7,
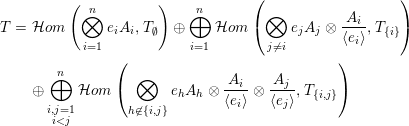 $$\begin{eqnarray}\displaystyle T & = & \displaystyle {\mathcal{H}}om\left(\mathop{\bigotimes }_{i=1}^{n}e_{i}A_{i},T_{\emptyset }\right)\oplus \bigoplus _{i=1}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{j\neq i}e_{j}A_{j}\otimes \frac{A_{i}}{\langle e_{i}\rangle },T_{\{i\}}\right)\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\substack{ i,j=1 \\ i<j}}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{h\not \in \{i,j\}}e_{h}A_{h}\otimes \frac{A_{i}}{\langle e_{i}\rangle }\otimes \frac{A_{j}}{\langle e_{j}\rangle },T_{\{i,j\}}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T & = & \displaystyle {\mathcal{H}}om\left(\mathop{\bigotimes }_{i=1}^{n}e_{i}A_{i},T_{\emptyset }\right)\oplus \bigoplus _{i=1}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{j\neq i}e_{j}A_{j}\otimes \frac{A_{i}}{\langle e_{i}\rangle },T_{\{i\}}\right)\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\substack{ i,j=1 \\ i<j}}^{n}{\mathcal{H}}om\left(\mathop{\bigotimes }_{h\not \in \{i,j\}}e_{h}A_{h}\otimes \frac{A_{i}}{\langle e_{i}\rangle }\otimes \frac{A_{j}}{\langle e_{j}\rangle },T_{\{i,j\}}\right)\nonumber\end{eqnarray}$$
is a tilting object provided that the two conditions of the theorem are satisfied. Again, the first condition is automatically satisfied as all of the tilting objects are in fact vector bundles. Furthermore, the second condition is also satisfied as
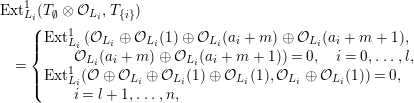 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Ext}_{L_{i}}^{1}(T_{\emptyset }\otimes {\mathcal{O}}_{L_{i}},T_{\{i\}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}l@{}}\operatorname{Ext}_{L_{i}}^{1} (\!{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m+1),\\ \qquad {\mathcal{O}}_{L_{i}}(a_{i}+m)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m+1)\!)=0,\quad i=0,\ldots ,l,\\ \operatorname{Ext}_{L_{i}}^{1}({\mathcal{O}}\oplus {\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(1),{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1))=0,\\ \qquad i=l+1,\ldots ,n,\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Ext}_{L_{i}}^{1}(T_{\emptyset }\otimes {\mathcal{O}}_{L_{i}},T_{\{i\}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}l@{}}\operatorname{Ext}_{L_{i}}^{1} (\!{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m+1),\\ \qquad {\mathcal{O}}_{L_{i}}(a_{i}+m)\oplus {\mathcal{O}}_{L_{i}}(a_{i}+m+1)\!)=0,\quad i=0,\ldots ,l,\\ \operatorname{Ext}_{L_{i}}^{1}({\mathcal{O}}\oplus {\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(1),{\mathcal{O}}_{L_{i}}\oplus {\mathcal{O}}_{L_{i}}(1))=0,\\ \qquad i=l+1,\ldots ,n,\end{array}\right.\nonumber\end{eqnarray}$$
since
![]() $a_{i}\geqslant -m$
, and so
$a_{i}\geqslant -m$
, and so
![]() $T$
is indeed a tilting bundle in
$T$
is indeed a tilting bundle in
![]() $\mathsf{mod}\,A$
.
$\mathsf{mod}\,A$
.
7.4 Squids
We have already seen the squid algebra that arose as the endomorphism algebra of tilting objects on GL weighted projective lines. We now generalize this to higher-dimensional GL weighted projective spaces.
Let
![]() $X=\mathbb{P}_{X_{0}:\ldots :X_{d}}^{d}$
, and for
$X=\mathbb{P}_{X_{0}:\ldots :X_{d}}^{d}$
, and for
![]() $i=1,\ldots ,n$
let
$i=1,\ldots ,n$
let
![]() $L_{i}:\ell _{i}(X_{0},\ldots ,X_{d})=0$
be hyperplanes in general position. For
$L_{i}:\ell _{i}(X_{0},\ldots ,X_{d})=0$
be hyperplanes in general position. For
![]() $I\subseteq \{1,\ldots ,n\}$
with
$I\subseteq \{1,\ldots ,n\}$
with
![]() $|I|\leqslant d$
,
$|I|\leqslant d$
,
is a tilting bundle in
![]() $\mathsf{coh}\,L_{I}$
, where
$\mathsf{coh}\,L_{I}$
, where
Furthermore, as we have seen, the category
![]() $\mathsf{mod}\,A$
, where
$\mathsf{mod}\,A$
, where
has a tilting object as described in Theorem 6.7, since the first condition is trivial as all
![]() $T_{I}$
are bundles, and the second condition is easy to verify with our choice of
$T_{I}$
are bundles, and the second condition is easy to verify with our choice of
![]() $T_{I}$
.
$T_{I}$
.
We now describe
![]() $\operatorname{End}_{A}(T)$
, where
$\operatorname{End}_{A}(T)$
, where
![]() $T$
is given by Theorem 6.7, presenting it as a quiver with relations. First, we describe the vertices, then the arrows, and finally the relations. For simplicity, we allow nonadmissible relations.
$T$
is given by Theorem 6.7, presenting it as a quiver with relations. First, we describe the vertices, then the arrows, and finally the relations. For simplicity, we allow nonadmissible relations.
7.4.1 Vertices
The vertices correspond to the indecomposable summands of
![]() $T$
. Writing
$T$
. Writing
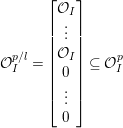 $$\begin{eqnarray}{\mathcal{O}}_{I}^{p/l}=\left[\begin{array}{@{}c@{}}{\mathcal{O}}_{I}\\ \vdots \\ {\mathcal{O}}_{I}\\ 0\\ \vdots \\ 0\end{array}\right]\subseteq {\mathcal{O}}_{I}^{p}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{I}^{p/l}=\left[\begin{array}{@{}c@{}}{\mathcal{O}}_{I}\\ \vdots \\ {\mathcal{O}}_{I}\\ 0\\ \vdots \\ 0\end{array}\right]\subseteq {\mathcal{O}}_{I}^{p}\end{eqnarray}$$
for the length
![]() $p$
-vectors such that the last
$p$
-vectors such that the last
![]() $l-1$
entries vanish, we may observe (see the discussion of functors above Theorem 6.7) that
$l-1$
entries vanish, we may observe (see the discussion of functors above Theorem 6.7) that
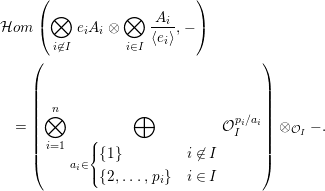 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{H}}om\left(\mathop{\bigotimes }_{i\not \in I}e_{i}A_{i}\otimes \bigotimes _{i\in I}\frac{A_{i}}{\langle e_{i}\rangle },-\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\mathop{\bigotimes }_{i=1}^{n}\mathop{\bigoplus }_{a_{i}\in \left\{\begin{array}{@{}ll@{}}\{1\}\quad & i\not \in I\\ \{2,\ldots ,p_{i}\}\quad & i\in I\end{array}\right.}{\mathcal{O}}_{I}^{p_{i}/a_{i}}\right)\otimes _{{\mathcal{O}}_{I}}-.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{H}}om\left(\mathop{\bigotimes }_{i\not \in I}e_{i}A_{i}\otimes \bigotimes _{i\in I}\frac{A_{i}}{\langle e_{i}\rangle },-\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\mathop{\bigotimes }_{i=1}^{n}\mathop{\bigoplus }_{a_{i}\in \left\{\begin{array}{@{}ll@{}}\{1\}\quad & i\not \in I\\ \{2,\ldots ,p_{i}\}\quad & i\in I\end{array}\right.}{\mathcal{O}}_{I}^{p_{i}/a_{i}}\right)\otimes _{{\mathcal{O}}_{I}}-.\nonumber\end{eqnarray}$$
Thus,
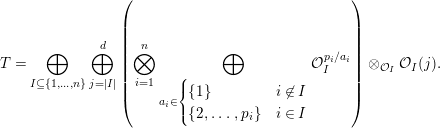 $$\begin{eqnarray}T=\bigoplus _{I\subseteq \{1,\ldots ,n\}}\mathop{\bigoplus }_{j=|I|}^{d}\left(\mathop{\bigotimes }_{i=1}^{n}\mathop{\bigoplus }_{a_{i}\in \left\{\begin{array}{@{}ll@{}}\{1\}\quad & i\not \in I\\ \{2,\ldots ,p_{i}\}\quad & i\in I\end{array}\right.}{\mathcal{O}}_{I}^{p_{i}/a_{i}}\right)\otimes _{{\mathcal{O}}_{I}}{\mathcal{O}}_{I}(j).\end{eqnarray}$$
$$\begin{eqnarray}T=\bigoplus _{I\subseteq \{1,\ldots ,n\}}\mathop{\bigoplus }_{j=|I|}^{d}\left(\mathop{\bigotimes }_{i=1}^{n}\mathop{\bigoplus }_{a_{i}\in \left\{\begin{array}{@{}ll@{}}\{1\}\quad & i\not \in I\\ \{2,\ldots ,p_{i}\}\quad & i\in I\end{array}\right.}{\mathcal{O}}_{I}^{p_{i}/a_{i}}\right)\otimes _{{\mathcal{O}}_{I}}{\mathcal{O}}_{I}(j).\end{eqnarray}$$
We note that, in total, the vector
![]() $\mathbf{a}$
runs over
$\mathbf{a}$
runs over
![]() $S$
, where
$S$
, where
![]() $S=\times _{i=1}^{n}\{1,\ldots ,p_{i}\}$
, as before. Thus, setting
$S=\times _{i=1}^{n}\{1,\ldots ,p_{i}\}$
, as before. Thus, setting
![]() $I_{\mathbf{a}}=\{i\mid a_{i}\neq 1\}$
, we may reorganize the above to
$I_{\mathbf{a}}=\{i\mid a_{i}\neq 1\}$
, we may reorganize the above to
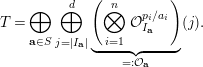 $$\begin{eqnarray}T=\bigoplus _{\mathbf{a}\in S}\mathop{\bigoplus }_{j=|I_{\mathbf{a}}|}^{d}\underbrace{\left(\mathop{\bigotimes }_{i=1}^{n}{\mathcal{O}}_{I_{\mathbf{a}}}^{p_{i}/a_{i}}\right)}_{=:{\mathcal{O}}_{\mathbf{a}}}(j).\end{eqnarray}$$
$$\begin{eqnarray}T=\bigoplus _{\mathbf{a}\in S}\mathop{\bigoplus }_{j=|I_{\mathbf{a}}|}^{d}\underbrace{\left(\mathop{\bigotimes }_{i=1}^{n}{\mathcal{O}}_{I_{\mathbf{a}}}^{p_{i}/a_{i}}\right)}_{=:{\mathcal{O}}_{\mathbf{a}}}(j).\end{eqnarray}$$
Thus, the vertices of the quiver are labeled
![]() ${\mathcal{O}}_{\mathbf{a}}(j)$
with
${\mathcal{O}}_{\mathbf{a}}(j)$
with
![]() $\mathbf{a}\in S$
and
$\mathbf{a}\in S$
and
![]() $|I_{\mathbf{a}}|\leqslant j\leqslant d$
.
$|I_{\mathbf{a}}|\leqslant j\leqslant d$
.
7.4.2 Arrows
-
∙
 $(d+1)$
arrows labeled
$(d+1)$
arrows labeled
 $X_{I_{\mathbf{a}}}^{0},\ldots ,X_{I_{\mathbf{a}}}^{d}$
between
$X_{I_{\mathbf{a}}}^{0},\ldots ,X_{I_{\mathbf{a}}}^{d}$
between
whenever
 $|I_{\mathbf{a}}|\leqslant j<d$
.
$|I_{\mathbf{a}}|\leqslant j<d$
. -
∙ One arrow labeled
 $y_{i}$
between when
$y_{i}$
between when $$\begin{eqnarray}{\mathcal{O}}_{\mathbf{a}}(j)\rightarrow {\mathcal{O}}_{\mathbf{a}+\mathbf{e}_{i}}(j)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\mathbf{a}}(j)\rightarrow {\mathcal{O}}_{\mathbf{a}+\mathbf{e}_{i}}(j)\end{eqnarray}$$
 $I_{\mathbf{a}+\mathbf{e}_{i}}\leqslant j\leqslant d$
.
$I_{\mathbf{a}+\mathbf{e}_{i}}\leqslant j\leqslant d$
.
7.4.3 Relations
-
∙ Commutativity relations:
 $X_{I_{\mathbf{a}}}^{i}X_{I_{\mathbf{a}}}^{j}=X_{I_{\mathbf{a}}}^{j}X_{I_{\mathbf{a}}}^{i},\;X_{I_{\mathbf{a}}}^{i}y_{j}=y_{j}X_{I_{\mathbf{a}+\mathbf{e}_{j}}}^{i},\;y_{i}y_{j}=y_{j}y_{i}$
whenever these compositions make sense.
$X_{I_{\mathbf{a}}}^{i}X_{I_{\mathbf{a}}}^{j}=X_{I_{\mathbf{a}}}^{j}X_{I_{\mathbf{a}}}^{i},\;X_{I_{\mathbf{a}}}^{i}y_{j}=y_{j}X_{I_{\mathbf{a}+\mathbf{e}_{j}}}^{i},\;y_{i}y_{j}=y_{j}y_{i}$
whenever these compositions make sense. -
∙
 $\ell _{i}(X_{I_{\mathbf{a}}}^{0},\ldots ,X_{I_{\mathbf{a}}}^{d})=0$
for all
$\ell _{i}(X_{I_{\mathbf{a}}}^{0},\ldots ,X_{I_{\mathbf{a}}}^{d})=0$
for all
 $\mathbf{a}\in S$
and
$\mathbf{a}\in S$
and
 $i\in I_{\mathbf{a}}$
.
$i\in I_{\mathbf{a}}$
. -
∙ For all
 $\mathbf{a}\in S$
and
$\mathbf{a}\in S$
and
 $i$
such that
$i$
such that
 $a_{i}=1$
, for any subquivers of the form
$a_{i}=1$
, for any subquivers of the form
we have the relation
 $$\begin{eqnarray}\ell _{j}(X_{I_{\mathbf{a}}}^{0},\ldots ,X_{I_{\mathbf{a}}}^{d})y_{i}=0.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{j}(X_{I_{\mathbf{a}}}^{0},\ldots ,X_{I_{\mathbf{a}}}^{d})y_{i}=0.\end{eqnarray}$$
Example 7.1. (On
 $\mathbb{P}^{2}$
with two weights
$\mathbb{P}^{2}$
with two weights
 $3$
and
$3$
and
 $3$
)
$3$
)
Consider
![]() $\mathbb{P}_{X_{0}:X_{1}:X_{2}}^{2}$
and hyperplanes
$\mathbb{P}_{X_{0}:X_{1}:X_{2}}^{2}$
and hyperplanes
![]() $L_{i}:\ell _{i}(X_{0},X_{1},X_{2})=0$
for
$L_{i}:\ell _{i}(X_{0},X_{1},X_{2})=0$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
 $$\begin{eqnarray}A=\left[\begin{array}{@{}ccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{1}) & {\mathcal{O}}(-L_{1})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}(-L_{1})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]\otimes \left[\begin{array}{@{}ccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{2}) & {\mathcal{O}}(-L_{2})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}(-L_{2})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]=A_{1}\otimes A_{2}.\end{eqnarray}$$
$$\begin{eqnarray}A=\left[\begin{array}{@{}ccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{1}) & {\mathcal{O}}(-L_{1})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}(-L_{1})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]\otimes \left[\begin{array}{@{}ccc@{}}{\mathcal{O}} & {\mathcal{O}}(-L_{2}) & {\mathcal{O}}(-L_{2})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}(-L_{2})\\ {\mathcal{O}} & {\mathcal{O}} & {\mathcal{O}}\end{array}\right]=A_{1}\otimes A_{2}.\end{eqnarray}$$
Then,
![]() $T_{\emptyset }={\mathcal{O}}\oplus {\mathcal{O}}(1)\oplus {\mathcal{O}}(2)$
,
$T_{\emptyset }={\mathcal{O}}\oplus {\mathcal{O}}(1)\oplus {\mathcal{O}}(2)$
,
![]() $T_{\{i\}}={\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(2)$
and
$T_{\{i\}}={\mathcal{O}}_{L_{i}}(1)\oplus {\mathcal{O}}_{L_{i}}(2)$
and
![]() $T_{\{1,2\}}={\mathcal{O}}_{L_{1}\cap L_{2}}$
. Then, by Theorem 6.7,
$T_{\{1,2\}}={\mathcal{O}}_{L_{1}\cap L_{2}}$
. Then, by Theorem 6.7,
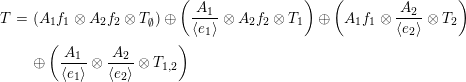 $$\begin{eqnarray}\displaystyle T & = & \displaystyle \left(A_{1}f_{1}\otimes A_{2}f_{2}\otimes T_{\emptyset }\right)\oplus \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes A_{2}f_{2}\otimes T_{1}\right)\oplus \left(A_{1}f_{1}\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \oplus \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{1,2}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T & = & \displaystyle \left(A_{1}f_{1}\otimes A_{2}f_{2}\otimes T_{\emptyset }\right)\oplus \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes A_{2}f_{2}\otimes T_{1}\right)\oplus \left(A_{1}f_{1}\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \oplus \left(\frac{A_{1}}{\langle e_{1}\rangle }\otimes \frac{A_{2}}{\langle e_{2}\rangle }\otimes T_{1,2}\right)\nonumber\end{eqnarray}$$
is a tilting object in
![]() ${\mathcal{A}}=\mathsf{mod}\,A$
.
${\mathcal{A}}=\mathsf{mod}\,A$
.
![]() $\operatorname{End}_{A}(T)$
is given by the following quiver:
$\operatorname{End}_{A}(T)$
is given by the following quiver:
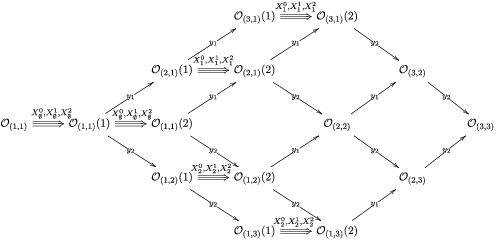
with commutativity relations as well as
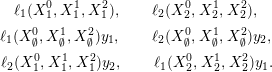 $$\begin{eqnarray}\displaystyle & \displaystyle \ell _{1}(X_{1}^{0},X_{1}^{1},X_{1}^{2}),\qquad \ell _{2}(X_{2}^{0},X_{2}^{1},X_{2}^{2}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \ell _{1}(X_{\emptyset }^{0},X_{\emptyset }^{1},X_{\emptyset }^{2})y_{1},\qquad \ell _{2}(X_{\emptyset }^{0},X_{\emptyset }^{1},X_{\emptyset }^{2})y_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \ell _{2}(X_{1}^{0},X_{1}^{1},X_{1}^{2})y_{2},\qquad \ell _{1}(X_{2}^{0},X_{2}^{1},X_{2}^{2})y_{1}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \ell _{1}(X_{1}^{0},X_{1}^{1},X_{1}^{2}),\qquad \ell _{2}(X_{2}^{0},X_{2}^{1},X_{2}^{2}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \ell _{1}(X_{\emptyset }^{0},X_{\emptyset }^{1},X_{\emptyset }^{2})y_{1},\qquad \ell _{2}(X_{\emptyset }^{0},X_{\emptyset }^{1},X_{\emptyset }^{2})y_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \ell _{2}(X_{1}^{0},X_{1}^{1},X_{1}^{2})y_{2},\qquad \ell _{1}(X_{2}^{0},X_{2}^{1},X_{2}^{2})y_{1}. & \displaystyle \nonumber\end{eqnarray}$$
Acknowledgments
Most of the work on this paper was done while the second author visited Nagoya. He would like to thank Osamu Iyama and his group for their hospitality. The first author thanks Daniel Chan for his valuable comments and suggestions. Both authors are deeply in debt to Osamu Iyama for providing many ideas, suggestions and comments to this project.