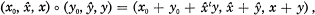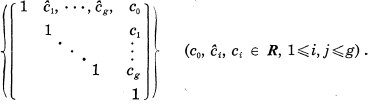Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Jae-Hyun
1991.
Harmonic analysis on the quotient spaces of Heisenberg groups.
Nagoya Mathematical Journal,
Vol. 123,
Issue. ,
p.
103.
Morikawa, Hisasi
1992.
Unitary representations of unipotent groups associated with theta series.
Nagoya Mathematical Journal,
Vol. 127,
Issue. ,
p.
167.