Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:14:46.633Z Has data issue: false hasContentIssue false
  • English
  • Français

Sous-algèbres birégulières d’une algèbre de Kac-Moody-Borcherds

Published online by Cambridge University Press:  22 January 2016

Nicole Bardy
Nicole Bardy*
Affiliation:
Institut Elie Cartan, U.M.R. 9973, Département de mathématiques de l’Université de Nancy I, B.P. 239 54506 Vandoeuvre-lès-Nancy Cedex, France, Nicole.Bardy-Panse@iecn.u-nancy.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 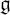be a Kac-Moody-Borcherds algebra on a field 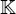associated to a symetrizable matrix and with Cartan subalgebra 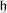. Let 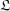be an ad 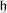-invariant subalgebra such that the restriction to 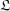of the standard bilinear form is nondegenerate. We show that the root system Ψ of 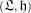is a subsystem according to [Ba] of 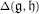. Moreover, if a subsystem Ω satisfies some conditions (i.e. Ω is “réduit et presque-clos”) of Ψ, we construct inside of 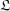a Kac-Moody-Borcherds algebra with root system Ω.

Let k be a subfield of 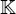. We prove similar results in the case of an action of a finite group of k-semi-automorphisms. In particular, we obtain a generalization to the Kac-Moody case of a result by Borel and Tits.

Let 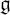be an almost-k-split form of a Kac-Moody algebra. We construct a Kac-Moody k-algebra with root system similar to the system of 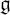(save on some multiples of certain roots).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 156 , 1999 , pp. 1 - 83
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1999

References

Références

[Ba] Bardy, N., Systèmes de racines infinis, Mémoires de la SMF, 65 (1996).Google Scholar
[Bbki, Lie] Bourbaki, N., Groupes et algèbres de Lie, Paris.Google Scholar
[Bo] Borcherds, R., Generalized Kac-Moody algebras, J. algebra, 115 (1989), 501–512.Google Scholar
[B-T] Borel, A. et Tits, J., Groupes réductifs, Publ. Math. I.H.E.S., 27 (1965).Google Scholar
[B3R] Back, V., Bardy, N., Ben-Messaoud, H. et Rousseau, G., Formes presque déployées d’algèbres de Kac-Moody: Classification et racines relatives, J. Algebra, 171 (1995), 43–96.Google Scholar
[D] Dynkin, B. E., Sous-algèbres semi-simples des algèbres semi-simples, Amer. math. Soc. Transl., Ser. 2, 6, 111–244.Google Scholar
[H] Humphreys, E. J., Linear algebraic groups, Springer-Verlag, 1975.Google Scholar
[K] Kac, G. V., Infinite dimensional Lie algebras, troisième édition, Cambridge University Press, 1990.Google Scholar
[M] Morita, J., Satured sets for generalized Cartan matrices, Tsukuba J. Math., 11 (1987), 77–91.Google Scholar
[N] Naito, S., On regular subalgebras of a symmetrizable Kac-Moody algebra, Proc. Japan Acad., 67 (1991), 117–121.Google Scholar
[T] Tits, J., Sous-algèbres des algèbres de Lie semi-simples, Séminaire Bourbaki, 119 (1955), 01–18.Google Scholar