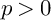1 Introduction
In the present article, rings are assumed to be commutative with a unity. Recently, Yves André established Perfectoid Abhyankar’s Lemma in [Reference André1] as a conceptual generalization of Almost Purity Theorem (see [Reference Scholze52, Th. 7.9]). This result is stated for perfectoid algebras over a perfectoid field, which are defined to be certain p-adically complete and separated rings. Using his results, André proved the existence of big Cohen–Macaulay algebras in mixed characteristic in [Reference André2]. More precisely, he constructed a certain almost Cohen–Macaulay algebra using perfectoids. We are inspired by this result and led to the following commutative algebra question, which is raised in [Reference Roberts49] and [Reference Roberts50] implicitly.
Question 1.1 (Roberts)
Let
![]() $(R,\frak {m})$
be a complete Noetherian local domain of arbitrary characteristic with its absolute integral closure
$(R,\frak {m})$
be a complete Noetherian local domain of arbitrary characteristic with its absolute integral closure
![]() $R^+$
. Then does there exist an R-algebra B such that B is an almost Cohen–Macaulay R-algebra and
$R^+$
. Then does there exist an R-algebra B such that B is an almost Cohen–Macaulay R-algebra and
![]() $R \subset B \subset R^+$
?
$R \subset B \subset R^+$
?
Essentially, Question 1.1 asks for a possibility to find a relatively small almost Cohen–Macaulay algebra. The structure of this article is twofold. We begin with giving an answer to Question 1.1 and then discuss necessary perfectoid techniques.
1.1 Main results on commutative algebra
André proved that any complete Noetherian local domain maps to a big Cohen–Macaulay algebra and using his result, it was proved that such a big Cohen–Macaulay algebra could be refined to be an integral perfectoid big Cohen–Macaulay algebra in [Reference Shimomoto58]. See Definitions 6.1 and 6.2 for big (almost) Cohen–Macaulay algebras. Question 1.1 was stated in a characteristic-free manner. Let us point out that if
![]() $\dim R \le 2$
, then
$\dim R \le 2$
, then
![]() $R^+$
is a big Cohen–Macaulay algebra in an arbitrary characteristic. This is easily seen by using Serre’s normality criterion. Recall that if R has prime characteristic
$R^+$
is a big Cohen–Macaulay algebra in an arbitrary characteristic. This is easily seen by using Serre’s normality criterion. Recall that if R has prime characteristic
![]() $p>0$
, then
$p>0$
, then
![]() $R^+$
is a big Cohen–Macaulay R-algebra. This result was proved by Hochster and Huneke and their proof is quite involved (see [Reference Hochster28]–[Reference Hochster and Huneke30], [Reference Huneke and Lyubeznik34], [Reference Quy48], and [Reference Sannai and Singh51] for related results as well as [Reference Heitmann and Ma26], [Reference Heitmann and Ma27], [Reference Ma and Schwede38], [Reference Murayama43], and [Reference Murayama44] for applications to tight closure, multiplier/test ideals, and singularities on algebraic varieties). There is another important work on the purity of Brauer groups using perfectoids (see [Reference Cesnavicius13]). It seems to be an open question whether
$R^+$
is a big Cohen–Macaulay R-algebra. This result was proved by Hochster and Huneke and their proof is quite involved (see [Reference Hochster28]–[Reference Hochster and Huneke30], [Reference Huneke and Lyubeznik34], [Reference Quy48], and [Reference Sannai and Singh51] for related results as well as [Reference Heitmann and Ma26], [Reference Heitmann and Ma27], [Reference Ma and Schwede38], [Reference Murayama43], and [Reference Murayama44] for applications to tight closure, multiplier/test ideals, and singularities on algebraic varieties). There is another important work on the purity of Brauer groups using perfectoids (see [Reference Cesnavicius13]). It seems to be an open question whether
![]() $R^+$
is almost Cohen–Macaulay when R has equal-characteristic zero. If R has mixed characteristic of dimension
$R^+$
is almost Cohen–Macaulay when R has equal-characteristic zero. If R has mixed characteristic of dimension
![]() $3$
, Heitmann proved that
$3$
, Heitmann proved that
![]() $R^+$
is a
$R^+$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay R-algebra in [Reference Heitmann24]. Our main concern, inspired also by the recent result of Heitmann and Ma [Reference Heitmann and Ma27], is to extend Heitmann’s result to the higher-dimensional case, thus giving a positive answer to Roberts’ question in mixed characteristic (see Theorem 6.5).
$(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay R-algebra in [Reference Heitmann24]. Our main concern, inspired also by the recent result of Heitmann and Ma [Reference Heitmann and Ma27], is to extend Heitmann’s result to the higher-dimensional case, thus giving a positive answer to Roberts’ question in mixed characteristic (see Theorem 6.5).
Main Theorem 1. Let
![]() $(R,\frak {m})$
be a complete Noetherian local domain of mixed characteristic
$(R,\frak {m})$
be a complete Noetherian local domain of mixed characteristic
![]() $p>0$
with perfect residue field k. Let
$p>0$
with perfect residue field k. Let
![]() $p,x_2,\ldots ,x_d$
be a system of parameters, and let
$p,x_2,\ldots ,x_d$
be a system of parameters, and let
![]() $R^+$
be the absolute integral closure of R. Then there exists an R-algebra T together with a nonzero element
$R^+$
be the absolute integral closure of R. Then there exists an R-algebra T together with a nonzero element
![]() $g \in R$
such that the following hold:
$g \in R$
such that the following hold:
-
1. T admits compatible systems of p-power roots
 $p^{\frac {1}{p^n}}, g^{\frac {1}{p^n}} \in T$
for all
$p^{\frac {1}{p^n}}, g^{\frac {1}{p^n}} \in T$
for all
 $n>0$
.
$n>0$
. -
2. The Frobenius endomorphism
 $Frob:T/(p) \to T/(p)$
is surjective.
$Frob:T/(p) \to T/(p)$
is surjective. -
3. T is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal domain with respect to
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal domain with respect to
 $p,x_2,\ldots ,x_d$
and
$p,x_2,\ldots ,x_d$
and
 $R \subset T \subset R^+$
.
$R \subset T \subset R^+$
. -
4. The p-adic completion
 $\widehat {T}$
is integral perfectoid.
$\widehat {T}$
is integral perfectoid. -
5.
 $R[\frac {1}{pg}] \to T[\frac {1}{pg}]$
is an ind-étale extension. In other words,
$R[\frac {1}{pg}] \to T[\frac {1}{pg}]$
is an ind-étale extension. In other words,
 $T[\frac {1}{pg}]$
is a filtered colimit of finite étale
$T[\frac {1}{pg}]$
is a filtered colimit of finite étale
 $R[\frac {1}{pg}]$
-algebras contained in
$R[\frac {1}{pg}]$
-algebras contained in
 $T[\frac {1}{pg}]$
.
$T[\frac {1}{pg}]$
.
In other words, one can find an almost Cohen–Macaulay, normal domain whose p-adic completion is integral perfectoid between R and its absolute integral closure. Using Hochster’s partial algebra modification and tilting, one can construct an integral perfectoid big Cohen–Macaulay R-algebra over T (see [Reference Shimomoto58] for details). In a sense, Main Theorem 1 is regarded as a weak analog of the mixed characteristic version of a result by Hochster and Huneke. The proof of our result does not seem to come by merely considering decompleted versions of the construction by Heitmann and Ma [Reference Heitmann and Ma27], due to the difficulty of studying
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost (or
$(pg)^{\frac {1}{p^{\infty }}}$
-almost (or
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost) mathematics under p-adic completion. For instance, we do not know if it is possible to decomplete André’s Riemann’s extension theorem (Theorem 8.1), because it is hard to analyze how the functor
$(g)^{\frac {1}{p^{\infty }}}$
-almost) mathematics under p-adic completion. For instance, we do not know if it is possible to decomplete André’s Riemann’s extension theorem (Theorem 8.1), because it is hard to analyze how the functor
![]() $g^{-\frac {1}{p^{\infty }}}(~)$
and the p-adic completion are related to each other.Footnote
1
This is the main reason one is required to redo the decompletion of André’s results in [Reference André1] and [Reference André2].
$g^{-\frac {1}{p^{\infty }}}(~)$
and the p-adic completion are related to each other.Footnote
1
This is the main reason one is required to redo the decompletion of André’s results in [Reference André1] and [Reference André2].
Finally, Bhatt recently proved that the absolute integral closure of a complete local domain
![]() $(R,\frak {m})$
of mixed characteristic has the property that
$(R,\frak {m})$
of mixed characteristic has the property that
![]() $R^+/p^nR^+$
is a balanced big Cohen–Macaulay
$R^+/p^nR^+$
is a balanced big Cohen–Macaulay
![]() $R/p^nR$
-algebra for any
$R/p^nR$
-algebra for any
![]() $n>0$
(see [Reference Bhatt7] in which the perfectoidization functor introduced in [Reference Bhatt and Scholze11] is used as an essential tool). It will be interesting to know how his methods and results are compared to ours; at present, the authors have no clue. However, it is worth pointing out the following fact.
$n>0$
(see [Reference Bhatt7] in which the perfectoidization functor introduced in [Reference Bhatt and Scholze11] is used as an essential tool). It will be interesting to know how his methods and results are compared to ours; at present, the authors have no clue. However, it is worth pointing out the following fact.
-
• The almost Cohen–Macaulay algebra T constructed in Main Theorem 1 is integral over the Noetherian local domain
 $(R,\frak {m})$
and much smaller than the absolute integral closure
$(R,\frak {m})$
and much smaller than the absolute integral closure
 $R^+$
.
$R^+$
.
In a sense, T is close to being a Noetherian ring. We mention some potential applications of Main Theorem 1.
-
1. Connections with the singularities studied in [Reference Ma and Schwede39] by exploiting the ind-étaleness of
 $R[\frac {1}{pg}] \to T[\frac {1}{pg}]$
.
$R[\frac {1}{pg}] \to T[\frac {1}{pg}]$
. -
2. A refined study of the main results on the closure operations in mixed characteristic as developed in [Reference Jiang35].
-
3. An explicit construction of a big Cohen–Macaulay module from the R-algebra T (see Corollary 6.10).
1.2 Main results on the decompletion of perfectoids and Riemann’s extension theorem
To prove Main Theorem 1, we need to relax the p-adic completeness from Perfectoid Abhyankar’s Lemma and incorporate the so-called Witt-perfect condition, which is introduced by Davis and Kedlaya [Reference Davis and Kedlaya15]. Roughly speaking, a Witt-perfect (or p-Witt-perfect) algebra is a p-torsion-free ring A whose p-adic completion becomes an integral perfectoid ring. Indeed, Davis and Kedlaya succeeded in proving the almost purity theorem for Witt-perfect rings. The present article is a sequel to authors’ previous work [Reference Nakazato and Shimomoto45], in which the authors were able to give a conceptual proof of the almost purity theorem by Davis–Kedlaya by analyzing the integral structure of Tate rings under completion. The advantage of working with Witt-perfect rings is that it allows one to take an infinite integral extension over a certain p-adically complete ring to construct an almost Cohen–Macaulay algebra. The resulting algebra is not p-adically complete, but its p-adic completion is integral perfectoid. Let us state the main result (see Theorem 5.20 and Proposition 5.21).
Main Theorem 2. Let A be a p-torsion-free algebra over a p-adically separated p-torsion-free Witt-perfect valuation domain V of rank
![]() $1$
admitting a compatible system of p-power roots
$1$
admitting a compatible system of p-power roots
![]() $p^{\frac {1}{p^n}} \in V$
, together with a regular element
$p^{\frac {1}{p^n}} \in V$
, together with a regular element
![]() $g \in A$
admitting a compatible system of p-power roots
$g \in A$
admitting a compatible system of p-power roots
![]() $g^{\frac {1}{p^n}} \in A$
. Suppose that the following conditions hold:
$g^{\frac {1}{p^n}} \in A$
. Suppose that the following conditions hold:
-
1. A is a p-adically Zariskian and normal ring.
-
2. A is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring. -
3. A is torsion-free and integral over a Noetherian normal domain R such that
 $g \in R$
and the height of the ideal
$g \in R$
and the height of the ideal
 $(p,g) \subset R$
is
$(p,g) \subset R$
is
 $2$
.
$2$
.Let us put
which is an A-subalgebra of $$ \begin{align*} g^{-\frac{1}{p^{\infty}}}A:=\Big\{a \in A[\frac{1}{g}]~\Big|~g^{\frac{1}{p^n}} a \in A,~\forall n>0\Big\}, \end{align*} $$
$$ \begin{align*} g^{-\frac{1}{p^{\infty}}}A:=\Big\{a \in A[\frac{1}{g}]~\Big|~g^{\frac{1}{p^n}} a \in A,~\forall n>0\Big\}, \end{align*} $$
 $A[\frac {1}{g}]$
. Let
$A[\frac {1}{g}]$
. Let
 $A[\frac {1}{pg}] \hookrightarrow B'$
be a finite étale extension, and denote by B the integral closure of
$A[\frac {1}{pg}] \hookrightarrow B'$
be a finite étale extension, and denote by B the integral closure of
 $g^{-\frac {1}{p^{\infty }}}A$
in
$g^{-\frac {1}{p^{\infty }}}A$
in
 $B'$
. Then the following statements hold:
$B'$
. Then the following statements hold:
-
(a) The Frobenius endomorphism
 $Frob:B/(p) \to B/(p)$
is
$Frob:B/(p) \to B/(p)$
is
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective and it induces an injection
$(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective and it induces an injection
 $B/(p^{\frac {1}{p}}) \hookrightarrow B/(p)$
.
$B/(p^{\frac {1}{p}}) \hookrightarrow B/(p)$
. -
(b) The induced map
 $A/(p^m) \to B/(p^m)$
is
$A/(p^m) \to B/(p^m)$
is
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale for all
$(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale for all
 $m>0$
.
$m>0$
.
-
In the original version of Perfectoid Abhyankar’s Lemma as proved in [Reference André1] and [Reference André2], it is assumed that A is an integral perfectoid ring, which is necessarily p-adically complete and separated. In Main Theorem 2, this assumption is weakened to p-adic Zariskianness. A detailed study of almost Witt-perfect rings appears in the article [Reference Nakazato and Shimomoto45] (see also Definition 5.2). The functor
![]() $A \mapsto g^{-\frac {1}{p^{\infty }}}A$
is called a functor of almost elements, which is fundamental in almost ring theory. The idea of the proof of Main Theorem 2 is to transport André’s original proof to our situation. Here is a summary of ingredients toward the proof:
$A \mapsto g^{-\frac {1}{p^{\infty }}}A$
is called a functor of almost elements, which is fundamental in almost ring theory. The idea of the proof of Main Theorem 2 is to transport André’s original proof to our situation. Here is a summary of ingredients toward the proof:
-
• The almost purity theorem for Witt-perfect rings.
-
• Descent to Galois extensions of commutative rings.
-
• Riemann’s extension theorem (Hebbarkeitssatz).
-
• Description of the integral structures of affinoid Tate rings via continuous valuations.
-
• Comparison of integral closure and complete integral closure.
The almost purity theorem for Witt-perfect rings is attributed to Davis and Kedlaya (see [Reference Davis and Kedlaya15], [Reference Davis and Kedlaya16]). A systematic approach to this important result was carried out in authors’ article [Reference Nakazato and Shimomoto45]. The almost purity theorem yields the assertion of Main Theorem 2 in the case when
![]() $g=1$
. To extend it to the general situations, we need a ring theoretic analog of Riemann’s Extension Theorem. Its perfectoid version has been proved by Scholze [Reference Scholze53], and André used it in the proof of Perfectoid Abhyankar’s Lemma in [Reference André1]. We establish two types of decompleted variant of it, which are at the core of the technical part of this article. The first one, which we call Zariskian Riemann’s extension theorem, is the following result (see Theorem 5.11). We should remark that it is independent of the theory of perfectoid rings.
$g=1$
. To extend it to the general situations, we need a ring theoretic analog of Riemann’s Extension Theorem. Its perfectoid version has been proved by Scholze [Reference Scholze53], and André used it in the proof of Perfectoid Abhyankar’s Lemma in [Reference André1]. We establish two types of decompleted variant of it, which are at the core of the technical part of this article. The first one, which we call Zariskian Riemann’s extension theorem, is the following result (see Theorem 5.11). We should remark that it is independent of the theory of perfectoid rings.
Main Theorem 3. Let A be a ring with a regular element t that is t-adically Zariskian and integral over a Noetherian ring. Let
![]() $g\in A$
be a regular element. Let
$g\in A$
be a regular element. Let
![]() $A^{j}$
be the Tate ring associated with
$A^{j}$
be the Tate ring associated with
![]() $\big (A[\frac {t^j}{g}], (t)\big )$
for every integer
$\big (A[\frac {t^j}{g}], (t)\big )$
for every integer
![]() $j>0$
(see Definition 2.8 for Tate rings). Then we have an isomorphism of rings
$j>0$
(see Definition 2.8 for Tate rings). Then we have an isomorphism of rings
 $$ \begin{align*}A^+_{A[\frac{1}{tg}]} \xrightarrow{\cong} \varprojlim_{j>0}A^{j\circ}, \end{align*} $$
$$ \begin{align*}A^+_{A[\frac{1}{tg}]} \xrightarrow{\cong} \varprojlim_{j>0}A^{j\circ}, \end{align*} $$
where the transition map
![]() $A^{j+1\circ }\to A^{j\circ }$
is the natural one, and
$A^{j+1\circ }\to A^{j\circ }$
is the natural one, and
![]() $A^+_{A[\frac {1}{tg}]}$
is the integral closure of A in
$A^+_{A[\frac {1}{tg}]}$
is the integral closure of A in
![]() $A[\frac {1}{tg}]$
.
$A[\frac {1}{tg}]$
.
For proving Main Theorem 3, a preliminary result Corollary 5.8 is crucial. Recall that an integrally closed domain A is the intersection of all valuation domains that lie between A and the field of fractions (see [Reference Swanson and Huneke59, Prop. 6.8.14] for the proof of this assertion from classical valuation theory). Corollary 5.8 is viewed as a variant of this result for affinoid Tate rings. The assumption that A is t-adically Zariskian and integral over a Noetherian ring is necessary in order to find valuation rings of rank
![]() $1$
for the proof to work (it is interesting to know to what extent one can relax these assumptions). Main Theorem 3 is also relevant to a standard technique used in non-archimedean geometry. Indeed, our proof for Proposition 5.7 is inspired by Huber’s description of integral structures of affinoid rings via continuous valuations (see [Reference Huber31, Lem. 3.3]). Moreover, one can formulate Corollary 5.8 as a variant of Fujiwara–Kato’s theorem (cf. [Reference Fujiwara and Kato19, II, Th. 8.1.11 and 8.2.19]) in rigid geometry (see Corollary 5.9 and Corollary 5.10).
$1$
for the proof to work (it is interesting to know to what extent one can relax these assumptions). Main Theorem 3 is also relevant to a standard technique used in non-archimedean geometry. Indeed, our proof for Proposition 5.7 is inspired by Huber’s description of integral structures of affinoid rings via continuous valuations (see [Reference Huber31, Lem. 3.3]). Moreover, one can formulate Corollary 5.8 as a variant of Fujiwara–Kato’s theorem (cf. [Reference Fujiwara and Kato19, II, Th. 8.1.11 and 8.2.19]) in rigid geometry (see Corollary 5.9 and Corollary 5.10).
The second variant, which we call Witt-perfect Riemann’s extension theorem, is stated as the assertions (c) and (d) of the following result (see Proposition 5.15 and Theorem 5.16 as well as the explanation of appearing notation).
Main Theorem 4. Let A be a p-torsion-free algebra over a p-adically separated p-torsion-free Witt-perfect valuation domain V of rank
![]() $1$
admitting a compatible system of p-power roots
$1$
admitting a compatible system of p-power roots
![]() $p^{\frac {1}{p^n}} \in V$
, together with a regular element
$p^{\frac {1}{p^n}} \in V$
, together with a regular element
![]() $g \in A$
admitting a compatible system of p-power roots
$g \in A$
admitting a compatible system of p-power roots
![]() $g^{\frac {1}{p^n}} \in A$
. Denote by
$g^{\frac {1}{p^n}} \in A$
. Denote by
![]() $\widehat {(~)}$
the p-adic completion and suppose that the following conditions hold:
$\widehat {(~)}$
the p-adic completion and suppose that the following conditions hold:
-
1. A is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring and completely integrally closed in
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring and completely integrally closed in
 $A[\frac {1}{p}]$
.
$A[\frac {1}{p}]$
. -
2.
 $(p,g)$
is a
$(p,g)$
is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A (which merely says that g is a
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A (which merely says that g is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost regular element on
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular element on
 $A/(p)$
).
$A/(p)$
).Then the following statements hold:
-
(a) The inclusion map:
(1.1)is a $$ \begin{align} A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big] \hookrightarrow A^{j \circ} \end{align} $$
$$ \begin{align} A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big] \hookrightarrow A^{j \circ} \end{align} $$
 $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
-
(b) There is an
 $A[\frac {p^{j}}{g}]$
-algebra isomorphism:
$A[\frac {p^{j}}{g}]$
-algebra isomorphism:  $$ \begin{align*}\widehat{A^{j\circ}} \xrightarrow{\cong} \mathcal{A}^{j\circ}. \end{align*} $$
$$ \begin{align*}\widehat{A^{j\circ}} \xrightarrow{\cong} \mathcal{A}^{j\circ}. \end{align*} $$
Moreover,
 $A^{j\circ }$
is Witt-perfect.
$A^{j\circ }$
is Witt-perfect. -
(c) We have the following identification of rings:
(1.2) $$ \begin{align} \varprojlim_{j>0}A^{j\circ}=A[\frac{1}{pg}]\times_{\mathcal{A}[\frac{1}{g}]}g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}. \end{align} $$
$$ \begin{align} \varprojlim_{j>0}A^{j\circ}=A[\frac{1}{pg}]\times_{\mathcal{A}[\frac{1}{g}]}g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}. \end{align} $$
-
(d) There is an injective A-algebra map:
whose cokernel is $$ \begin{align*}\widehat{\varprojlim_{j>0} A^{j\circ}} \hookrightarrow \varprojlim_{j>0} \widehat{A^{j\circ}}, \end{align*} $$
$$ \begin{align*}\widehat{\varprojlim_{j>0} A^{j\circ}} \hookrightarrow \varprojlim_{j>0} \widehat{A^{j\circ}}, \end{align*} $$
 $(g)^{\frac {1}{p^{\infty }}}$
-almost zero.
$(g)^{\frac {1}{p^{\infty }}}$
-almost zero.
-
The almost isomorphism in the assertion (d) is at the heart of the theorem; notice that in general, inverse limits and taking completion do not commute. Our proof for the assertions (c) and (d) relies on the already-known Riemann’s extension theorem for perfectoid algebras. Thus, we need to describe the relationship between rational localizations of Tate rings associated with a Witt-perfect ring and the corresponding integral perfectoid ring. The assertions (a) and (b) are consequences of a fine study on it. The
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost regularity assumption on the sequence
$(p)^{\frac {1}{p^{\infty }}}$
-almost regularity assumption on the sequence
![]() $(p,g)$
ensures that g is
$(p,g)$
ensures that g is
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost regular on the p-adic completion
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular on the p-adic completion
![]() $\widehat {A}$
; this is due to Lemma 3.11. Another reason for assuming
$\widehat {A}$
; this is due to Lemma 3.11. Another reason for assuming
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost regularity rather than
$(p)^{\frac {1}{p^{\infty }}}$
-almost regularity rather than
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost regularity is due to Lemma 5.14 (see also Proposition 3.14 as an intermediary step). We remark that there are no common assumptions of both Main Theorems 3 and 4 on the ring A. Let us summarize the content of each section of the present article.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost regularity is due to Lemma 5.14 (see also Proposition 3.14 as an intermediary step). We remark that there are no common assumptions of both Main Theorems 3 and 4 on the ring A. Let us summarize the content of each section of the present article.
In §2, we give generalities on almost rings, almost modules, and topological rings. We also recall the definitions of perfectoid algebras and their almost analogs whose detailed studies are given in the authors’ article [Reference Nakazato and Shimomoto45].
In §3, some basic results are proved on complete integral closure and its behavior under completion. We stress that the use of “Beauville–Laszlo’s lemma” is indispensable for getting meaningful results. This section is intended to give some justification/clarification on the difference between integral and complete integral closures.
In §4, we study some behavior of finite étale extensions of Tate rings under rational localization. This section is regarded as a complement to [Reference Nakazato and Shimomoto45], and so also includes a brief review of several results in that article.
In §5, we establish the decompleted variants of Riemann’s extension theorem as well as Perfectoid Abhyankar’s lemma over almost perfectoid rings. As this section contains quite technical discussions, the reader can skip the details on first reading.
In §6, we give the main applications of the results obtained in the previous sections. The main theorem asserts that one can construct an almost Cohen–Macaulay normal domain between the original complete local domain and its absolute integral closure.
In §7, we prove auxiliary facts on integrality as well as almost integrality via rigid analytic methods, following the book [Reference Fujiwara and Kato19].
In §8, we give a complete account of the proof of André’s Riemann’s extension theorem. To this aim, we also give a proof of the almost vanishing theorem on derived limits, which is discussed in [Reference André1]. We hope that this appendix will be helpful for the reader to understand key results in André’s original approach.
In §9, we give a brief account on (almost) Galois extensions of commutative rings. These are already treated in André’s article [Reference André1] and we omit the proofs.
Caution: In this article, we take both integral closure and complete integral closure for a given ring extension. This distinction is not essential in our setting in view of Proposition 7.1. However, we opt to formulate the results (mostly) in complete integral closure, because we believe that correct statements of the possible generalizations of our main results without integrality over a Noetherian ring should be given in terms of complete integral closure. The reader is warned that complete integral closure is coined as total integral closure in the lecture notes [Reference Bhatt8]. We collect notation used in the proof of Theorem 5.20 in Definition 5.12 (see also Remark 5.13).
The almost version of perfectoid or Witt-perfect rings often appears in the following discussions. To the best of our knowledge, the first appearance of almost perfectoid rings came from André’s work on Perfectoid Abhyankar’s Lemma. The reason is that
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost mathematics is essential in André’s work, in which case, we can only say that the cokernel of the Frobenius map is
$(pg)^{\frac {1}{p^{\infty }}}$
-almost mathematics is essential in André’s work, in which case, we can only say that the cokernel of the Frobenius map is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-surjective. The reader will notice that the base ring in Theorem 5.20 is required to be almost Witt-perfect in order for the proof to work. In a future’s occasion, we hope to clarify a real distinction between perfectoid and almost perfectoid rings.
$(pg)^{\frac {1}{p^{\infty }}}$
-surjective. The reader will notice that the base ring in Theorem 5.20 is required to be almost Witt-perfect in order for the proof to work. In a future’s occasion, we hope to clarify a real distinction between perfectoid and almost perfectoid rings.
2 Notation and conventions
We say that a commutative ring A is normal, if the localization
![]() $A_{\frak {p}}$
is an integrally closed domain in its field of fractions for every prime ideal
$A_{\frak {p}}$
is an integrally closed domain in its field of fractions for every prime ideal
![]() $\frak {p} \subset A$
. For ring maps
$\frak {p} \subset A$
. For ring maps
![]() $A \to C$
and
$A \to C$
and
![]() $B \to C$
, we write
$B \to C$
, we write
![]() $A \times _C B$
for the fiber product. The completion of a module is always taken to be complete and separated.
$A \times _C B$
for the fiber product. The completion of a module is always taken to be complete and separated.
2.1 Almost ring theory
We use language of almost ring theory. The most comprehensive references are [Reference Gabber and Ramero20] and [Reference Gabber and Ramero21], where the latter discusses applications of almost ring theory to algebraic geometry and commutative ring theory. Notably, it includes an extension of the Direct Summand Conjecture to the setting of log-regular rings. Throughout this article, for an integral domain A, let
![]() $\operatorname {Frac}(A)$
denote the field of fractions of A. A basic setup is a pair
$\operatorname {Frac}(A)$
denote the field of fractions of A. A basic setup is a pair
![]() $(A,I)$
, where A is a ring and I is its ideal such that
$(A,I)$
, where A is a ring and I is its ideal such that
![]() $I^2=I$
.Footnote
2
An A-module M is I-almost zero (or simply almost zero) if
$I^2=I$
.Footnote
2
An A-module M is I-almost zero (or simply almost zero) if
![]() $I M=0$
. Let
$I M=0$
. Let
![]() $f:M \to N$
be an A-module map. Then we say that f is I-almost injective (resp. I-almost surjective if the kernel (resp. cokernel) of f is annihilated by I. Moreover, we say that f is an I-almost isomorphism (or simply an almost isomorphism) if both kernel and cokernel of f are annihilated by I. Let us define an important class of basic setup
$f:M \to N$
be an A-module map. Then we say that f is I-almost injective (resp. I-almost surjective if the kernel (resp. cokernel) of f is annihilated by I. Moreover, we say that f is an I-almost isomorphism (or simply an almost isomorphism) if both kernel and cokernel of f are annihilated by I. Let us define an important class of basic setup
![]() $(K,I)$
as follows: Let K be a perfectoid field of characteristic 0 with a non-archimedean norm
$(K,I)$
as follows: Let K be a perfectoid field of characteristic 0 with a non-archimedean norm
![]() $|\cdot |:K \to \mathbf {R}_{\ge 0}$
. Fix an element
$|\cdot |:K \to \mathbf {R}_{\ge 0}$
. Fix an element
![]() $\varpi \in K$
such that
$\varpi \in K$
such that
![]() $|p| \le |\varpi |<1$
and
$|p| \le |\varpi |<1$
and
![]() $I:=\bigcup _{n>0} \varpi ^{\frac {1}{p^n}}K^{\circ }$
(such an element
$I:=\bigcup _{n>0} \varpi ^{\frac {1}{p^n}}K^{\circ }$
(such an element
![]() $\varpi $
exists and plays a fundamental role in perfectoid geometry). Set
$\varpi $
exists and plays a fundamental role in perfectoid geometry). Set
![]() $K^{\circ }:=\{x \in K~|~|x| \le 1\}$
and
$K^{\circ }:=\{x \in K~|~|x| \le 1\}$
and
![]() $K^{\circ \circ }:=\{x \in K~|~|x| < 1\}$
. Then
$K^{\circ \circ }:=\{x \in K~|~|x| < 1\}$
. Then
![]() $K^{\circ }$
is a complete valuation domain of rank
$K^{\circ }$
is a complete valuation domain of rank
![]() $1$
with field of fractions K and the pair
$1$
with field of fractions K and the pair
![]() $(K^{\circ },I)$
is a basic setup.
$(K^{\circ },I)$
is a basic setup.
Let
![]() $(A,I)$
be a basic setup. Then the category of almost A-modules or
$(A,I)$
be a basic setup. Then the category of almost A-modules or
![]() $A^a$
-modules
$A^a$
-modules
![]() $A^a-\mathbf {Mod}$
, is the quotient category of A-modules
$A^a-\mathbf {Mod}$
, is the quotient category of A-modules
![]() $A-\mathbf {Mod}$
by the Serre subcategory of I-almost zero modules. So this defines the localization functor
$A-\mathbf {Mod}$
by the Serre subcategory of I-almost zero modules. So this defines the localization functor
![]() $(~)^a:A-\mathbf {Mod} \to A^a-\mathbf {Mod}$
. This functor admits a right adjoint and a left adjoint functors, respectively:
$(~)^a:A-\mathbf {Mod} \to A^a-\mathbf {Mod}$
. This functor admits a right adjoint and a left adjoint functors, respectively:
These are defined by
![]() $M_*:=\operatorname {Hom}_A(I,M_0)$
with
$M_*:=\operatorname {Hom}_A(I,M_0)$
with
![]() $M_0^a=M$
and
$M_0^a=M$
and
![]() $M_!:=I \otimes _A M_*$
(see [Reference Gabber and Ramero20, Prop. 2.2.14 and 2.2.23] for these functors). So we have the following fact: The functor
$M_!:=I \otimes _A M_*$
(see [Reference Gabber and Ramero20, Prop. 2.2.14 and 2.2.23] for these functors). So we have the following fact: The functor
![]() $(~)_*$
commutes with limits and
$(~)_*$
commutes with limits and
![]() $(~)_!$
commutes with colimits. Finally, the functor
$(~)_!$
commutes with colimits. Finally, the functor
![]() $(~)^a$
commutes with both colimits and limits. In particular, an explicit description of
$(~)^a$
commutes with both colimits and limits. In particular, an explicit description of
![]() $M_*$
will be helpful. Henceforth, we abusively write
$M_*$
will be helpful. Henceforth, we abusively write
![]() $M_*$
for
$M_*$
for
![]() $(M^a)_*$
for an A-module M. The notation
$(M^a)_*$
for an A-module M. The notation
![]() $ M \xrightarrow {\approx } N$
will be used throughout to indicate that there is an A-homomorphism
$ M \xrightarrow {\approx } N$
will be used throughout to indicate that there is an A-homomorphism
![]() $M \to N$
that is an I-almost isomorphism. An isomorphism in the category
$M \to N$
that is an I-almost isomorphism. An isomorphism in the category
![]() $A^a-\mathbf {Mod}$
will be denoted by
$A^a-\mathbf {Mod}$
will be denoted by
![]() $M \approx N$
.Footnote
3
For technical details, we refer the reader to [Reference Gabber and Ramero20].
$M \approx N$
.Footnote
3
For technical details, we refer the reader to [Reference Gabber and Ramero20].
Let us recall an explicit description of
![]() $M_{*}$
.
$M_{*}$
.
Lemma 2.1. Let M be a module over a ring A, and let
![]() $\varpi \in A$
be an element such that A admits a compatible system of p-power roots
$\varpi \in A$
be an element such that A admits a compatible system of p-power roots
![]() $\varpi ^{\frac {1}{p^n}} \in A$
for
$\varpi ^{\frac {1}{p^n}} \in A$
for
![]() $n \ge 0$
. Set
$n \ge 0$
. Set
![]() $I=\bigcup _{n>0} \varpi _n A$
with
$I=\bigcup _{n>0} \varpi _n A$
with
![]() $\varpi _n:=\varpi ^{\frac {1}{p^n}}$
and suppose that
$\varpi _n:=\varpi ^{\frac {1}{p^n}}$
and suppose that
![]() $\varpi $
is regular on both A and M. Then the following statements hold:
$\varpi $
is regular on both A and M. Then the following statements hold:
-
1.
 $(A,I)$
is a basic setup.
$(A,I)$
is a basic setup. -
2. There is an equality:
Moreover, the natural map $$ \begin{align*}M_*=\Big\{b \in M[\frac{1}{\varpi}]~\Big|~\varpi_n b \in M~ \mbox{for all}~n>0\Big\}. \end{align*} $$
$$ \begin{align*}M_*=\Big\{b \in M[\frac{1}{\varpi}]~\Big|~\varpi_n b \in M~ \mbox{for all}~n>0\Big\}. \end{align*} $$
 $M \to M_*$
is an I-almost isomorphism. If M is an A-algebra, then
$M \to M_*$
is an I-almost isomorphism. If M is an A-algebra, then
 $M_*$
has an A-algebra structure and the natural map
$M_*$
has an A-algebra structure and the natural map
 $M \to M_*$
is an A-algebra map.
$M \to M_*$
is an A-algebra map.
Proof. The presentation for
![]() $M_*$
is found in [Reference Scholze52, Lem. 5.3] over a perfectoid field and the proof there works under our setting without any modifications. If M is an A-algebra, then the above presentation will endow
$M_*$
is found in [Reference Scholze52, Lem. 5.3] over a perfectoid field and the proof there works under our setting without any modifications. If M is an A-algebra, then the above presentation will endow
![]() $M_*$
with an A-algebra structure. In other words,
$M_*$
with an A-algebra structure. In other words,
![]() $M_*$
is naturally an A-subring of
$M_*$
is naturally an A-subring of
![]() $M[\frac {1}{\varpi }]$
.
$M[\frac {1}{\varpi }]$
.
In the situation of the lemma, we often write
![]() $M_*$
as
$M_*$
as
![]() $\bigcap _{n>0} \varpi ^{-\frac {1}{p^n}}M$
or
$\bigcap _{n>0} \varpi ^{-\frac {1}{p^n}}M$
or
![]() $\varpi ^{-\frac {1}{p^{\infty }}}M$
to indicate that what basic setup of almost ring theory we are talking. Next, we observe that I-almost isomorphy is preserved under pullbacks in the category of (actual) A-algebras.
$\varpi ^{-\frac {1}{p^{\infty }}}M$
to indicate that what basic setup of almost ring theory we are talking. Next, we observe that I-almost isomorphy is preserved under pullbacks in the category of (actual) A-algebras.
Lemma 2.2. Let
![]() $(A, I)$
be a basic setup. Let
$(A, I)$
be a basic setup. Let
![]() $f: R\to S$
be an A-algebra homomorphism that admits a commutative diagram of A-algebras:
$f: R\to S$
be an A-algebra homomorphism that admits a commutative diagram of A-algebras:

Let
![]() $\psi : T'\to T$
be an A-algebra homomorphism. Then the following assertions hold:
$\psi : T'\to T$
be an A-algebra homomorphism. Then the following assertions hold:
-
1. If f is I-almost injective (i.e.,
 $\operatorname {Ker} (f)$
is annihilated by I), then so is the base extension
$\operatorname {Ker} (f)$
is annihilated by I), then so is the base extension
 $\operatorname {id}_{T'}\times _{T}f: T'\times _{T}R\to T'\times _{T}S$
.
$\operatorname {id}_{T'}\times _{T}f: T'\times _{T}R\to T'\times _{T}S$
. -
2. If f is I-almost surjective (i.e.,
 $\operatorname {Coker} (f)$
is annihilated by I), then so is the base extension
$\operatorname {Coker} (f)$
is annihilated by I), then so is the base extension
 $\operatorname {id}_{T'}\times _{T}f: T'\times _{T}R\to T'\times _{T}S$
.
$\operatorname {id}_{T'}\times _{T}f: T'\times _{T}R\to T'\times _{T}S$
.
Proof. We use the explicit description of fiber products:
![]() $T'\times _{T}R=\{(t',r) \in T'\times R~|~\psi (t')=\varphi _{R}(r)\}$
and
$T'\times _{T}R=\{(t',r) \in T'\times R~|~\psi (t')=\varphi _{R}(r)\}$
and
![]() $T'\times _{T}S=\{(t',s) \in T'\times S~|~\psi (t')=\varphi _{S}(s)\}$
.
$T'\times _{T}S=\{(t',s) \in T'\times S~|~\psi (t')=\varphi _{S}(s)\}$
.
(1): Pick an element
![]() $(t',r)\in T'\times _{T}R$
with
$(t',r)\in T'\times _{T}R$
with
![]() $\operatorname {id}_{T'}\times _{T}f((t',r))=0$
. Then
$\operatorname {id}_{T'}\times _{T}f((t',r))=0$
. Then
![]() $t'=\operatorname {id}_{T'}(t')=0$
. Moreover, since
$t'=\operatorname {id}_{T'}(t')=0$
. Moreover, since
![]() $f(r)=0$
,
$f(r)=0$
,
![]() $xs=0$
for every
$xs=0$
for every
![]() $x\in I$
by assumption. Hence
$x\in I$
by assumption. Hence
![]() $x(t',r)=0$
for every
$x(t',r)=0$
for every
![]() $x\in I$
, which yields the assertion.
$x\in I$
, which yields the assertion.
(2): Pick an element
![]() $(t',s)\in T'\times _{T}S$
. Then by assumption, for every
$(t',s)\in T'\times _{T}S$
. Then by assumption, for every
![]() $x\in I$
, there exists some
$x\in I$
, there exists some
![]() $r_{x}\in R$
such that
$r_{x}\in R$
such that
![]() $f(r_{x})=xs$
. Thus, we obtain an element
$f(r_{x})=xs$
. Thus, we obtain an element
![]() $(xt', r_{x})\in T'\times _{T}R$
whose image in
$(xt', r_{x})\in T'\times _{T}R$
whose image in
![]() $T'\times _{T}S$
is
$T'\times _{T}S$
is
![]() $x(t', s)$
, as desired.
$x(t', s)$
, as desired.
The following lemma claims that almost isomorphy is preserved under adic completion.
Lemma 2.3. Let
![]() $(A, I)$
be a basic setup. Let
$(A, I)$
be a basic setup. Let
![]() $f: M\to N$
be an I-almost isomorphism between A-modules. Let
$f: M\to N$
be an I-almost isomorphism between A-modules. Let
![]() $J\subset A$
be an ideal, and let
$J\subset A$
be an ideal, and let
![]() $\widehat {M}$
and
$\widehat {M}$
and
![]() $\widehat {N}$
be the J-adic completions. Then the A-module map
$\widehat {N}$
be the J-adic completions. Then the A-module map
![]() $\widehat {f}: \widehat {M}\to \widehat {N}$
induced by f is also an I-almost isomorphism.
$\widehat {f}: \widehat {M}\to \widehat {N}$
induced by f is also an I-almost isomorphism.
Proof. The assertion is equivalent to the assertion that the map
![]() $(\widehat {f})^{a}: (\widehat {M})^{a}\to (\widehat {N})^{a}$
in
$(\widehat {f})^{a}: (\widehat {M})^{a}\to (\widehat {N})^{a}$
in
![]() $A^a-\mathbf {Mod}$
is an isomorphism. Since the functor
$A^a-\mathbf {Mod}$
is an isomorphism. Since the functor
![]() $(~)^a$
commutes with limits,
$(~)^a$
commutes with limits,
![]() $(\widehat {f})^{a}$
is canonically isomorphic to
$(\widehat {f})^{a}$
is canonically isomorphic to
![]() $\varprojlim _{n>0}f^{a}_{n}: \varprojlim _{n>0}(M/J^{n}M)^{a}\to \varprojlim _{n>0}(N/J^{n}N)^{a}$
, where
$\varprojlim _{n>0}f^{a}_{n}: \varprojlim _{n>0}(M/J^{n}M)^{a}\to \varprojlim _{n>0}(N/J^{n}N)^{a}$
, where
![]() $f_{n}: M/J^{n}M\to N/J^{n}N$
is the A-module map induced by f for every
$f_{n}: M/J^{n}M\to N/J^{n}N$
is the A-module map induced by f for every
![]() $n> 0$
. Thus, it suffices to show that
$n> 0$
. Thus, it suffices to show that
![]() $f_{n}$
is an I-almost isomorphism for every
$f_{n}$
is an I-almost isomorphism for every
![]() $n> 0$
. It can be easily seen that
$n> 0$
. It can be easily seen that
![]() $f_{n}$
is I-almost surjective because f is so. Let us verify that
$f_{n}$
is I-almost surjective because f is so. Let us verify that
![]() $f_{n}$
is I-almost injective. First, we have
$f_{n}$
is I-almost injective. First, we have
![]() $\operatorname {Ker} (f_{n})=f^{-1}(J^{n}N)/J^{n}M$
. Moreover, for an arbitrary
$\operatorname {Ker} (f_{n})=f^{-1}(J^{n}N)/J^{n}M$
. Moreover, for an arbitrary
![]() $\epsilon \in I$
,
$\epsilon \in I$
,
because f is I-almost surjective. Thus, since f is I-almost injective, for an arbitrary
![]() $\epsilon '\in I$
, we have
$\epsilon '\in I$
, we have
Therefore,
![]() $\epsilon '\epsilon \operatorname {Ker} (f_{n})=0$
. Since
$\epsilon '\epsilon \operatorname {Ker} (f_{n})=0$
. Since
![]() $I^{2}=I$
, it implies that
$I^{2}=I$
, it implies that
![]() $\epsilon " \operatorname {Ker} (f_{n})=0$
for every
$\epsilon " \operatorname {Ker} (f_{n})=0$
for every
![]() $\epsilon "\in I$
. Hence, the assertion follows.
$\epsilon "\in I$
. Hence, the assertion follows.
2.2 Integrality and almost integrality
Here, we list several closure operations of rings that will be used frequently.
Definition 2.4. Let
![]() $R \subset S$
be a ring extension.
$R \subset S$
be a ring extension.
-
1. An element
 $s \in S$
is integral over R, if
$s \in S$
is integral over R, if
 $\sum _{n=0}^{\infty } R \cdot s^n$
is a finitely generated R-submodule of S. The set of all elements denoted as T of S that are integral over R forms a subring of S. If
$\sum _{n=0}^{\infty } R \cdot s^n$
is a finitely generated R-submodule of S. The set of all elements denoted as T of S that are integral over R forms a subring of S. If
 $R=T$
, then R is called integrally closed in S. We denote by
$R=T$
, then R is called integrally closed in S. We denote by
 $R^+_S$
the integral closure of R in S.
$R^+_S$
the integral closure of R in S. -
2. An element
 $s \in S$
is almost integral over R, if
$s \in S$
is almost integral over R, if
 $\sum _{n=0}^{\infty } R \cdot s^n$
is contained in a finitely generated R-submodule of S. The set of all elements denoted as T of S that are almost integral over R forms a subring of S, which is called the complete integral closure of R in S. We denote this ring by
$\sum _{n=0}^{\infty } R \cdot s^n$
is contained in a finitely generated R-submodule of S. The set of all elements denoted as T of S that are almost integral over R forms a subring of S, which is called the complete integral closure of R in S. We denote this ring by
 $R^*_S$
. If
$R^*_S$
. If
 $R=T$
, then R is called completely integrally closed in S.
$R=T$
, then R is called completely integrally closed in S.
This definition can be extended to any ring map
![]() $R \to S$
in a natural way, as follows. Let R be a ring, let S be an R-algebra, and let
$R \to S$
in a natural way, as follows. Let R be a ring, let S be an R-algebra, and let
![]() $s\in S$
be an element. Then we say that s is integral (resp. almost integral) over R, if s is integral (resp. almost integral) over the image of R in S. We should remark that “almost integrality” does not mean “integrality in almost ring theory” in a strict sense, but there is an interesting connection between these two notions (see [Reference Nakazato and Shimomoto45, Lem. 5.3]).
$s\in S$
be an element. Then we say that s is integral (resp. almost integral) over R, if s is integral (resp. almost integral) over the image of R in S. We should remark that “almost integrality” does not mean “integrality in almost ring theory” in a strict sense, but there is an interesting connection between these two notions (see [Reference Nakazato and Shimomoto45, Lem. 5.3]).
From the definition, it is immediate to see that if R is a Noetherian domain and S is the field of fractions of R, then R is integrally closed if and only if it is completely integrally closed. There are subtle points that we must be careful about on complete integral closure. The complete integral closure T of R is not necessarily completely integrally closed in S and such an example was constructed by Heinzer [Reference Heinzer23]. Let
![]() $R \subset S \subset T$
be ring extensions. Let
$R \subset S \subset T$
be ring extensions. Let
![]() $b \in S$
be an element. Assume that b is almost integral over R when b is regarded as an element of T. Then it does not necessarily mean that b is almost integral over R when b is regarded as an element of S (see [Reference Gilmer and Heinzer22] for such an example).
$b \in S$
be an element. Assume that b is almost integral over R when b is regarded as an element of T. Then it does not necessarily mean that b is almost integral over R when b is regarded as an element of S (see [Reference Gilmer and Heinzer22] for such an example).
We also recall the notion of absolute integral closure due to Artin [Reference Artin4].
Definition 2.5 (Absolute integral closure)
Let A be an integral domain. Then the absolute integral closure of A denoted by
![]() $A^+$
, is defined to be the integral closure of A in a fixed algebraic closure of
$A^+$
, is defined to be the integral closure of A in a fixed algebraic closure of
![]() $\operatorname {Frac}(A)$
.
$\operatorname {Frac}(A)$
.
2.3 Semivaluation and adic spectra
We need some basic language from Huber’s continuous valuations and adic spectra (see [Reference Huber31], [Reference Huber32]). Continuous valuations are a special class of semivaluations (see Definition 2.6) that satisfy a certain topological condition.
Definition 2.6 (Semivaluation)
Let A be a ring, and let
![]() $|\cdot |:A \to \Gamma \cup \{0\}$
be a map for a totally ordered abelian group
$|\cdot |:A \to \Gamma \cup \{0\}$
be a map for a totally ordered abelian group
![]() $\Gamma $
with group unit
$\Gamma $
with group unit
![]() $1,$
and we let
$1,$
and we let
![]() $0< \gamma $
for arbitrary
$0< \gamma $
for arbitrary
![]() $\gamma \in \Gamma $
. Then
$\gamma \in \Gamma $
. Then
![]() $|\cdot |$
is called a semivaluation, if
$|\cdot |$
is called a semivaluation, if
![]() $|0|=0$
,
$|0|=0$
,
![]() $|1|=1$
,
$|1|=1$
,
![]() $|xy|=|x||y|$
and
$|xy|=|x||y|$
and
![]() $|x+y| \le \max \{|x|,|y|\}$
for
$|x+y| \le \max \{|x|,|y|\}$
for
![]() $x,y \in A$
.
$x,y \in A$
.
Definition 2.7 (Continuous valuation)
Let A be a topological ring. Then a semivaluation
![]() $|\cdot |:A \to \Gamma \cup \{0\}$
is continuous if
$|\cdot |:A \to \Gamma \cup \{0\}$
is continuous if
![]() $|\cdot |^{-1}(\Gamma _{<\gamma } \cup \{0\})$
is an open subset of A for any
$|\cdot |^{-1}(\Gamma _{<\gamma } \cup \{0\})$
is an open subset of A for any
![]() $\gamma \in \Gamma $
, where
$\gamma \in \Gamma $
, where
![]() $\Gamma _{<\gamma }:=\{\alpha \in \Gamma ~|~\alpha <\gamma \}$
.
$\Gamma _{<\gamma }:=\{\alpha \in \Gamma ~|~\alpha <\gamma \}$
.
The name “semivaluation” refers to the fact that A need not be an integral domain. However, following the usage employed in [Reference Huber31], we will stick to the word “continuous valuation” rather than “continuous semivaluation” for brevity.
In this article, we mainly consider continuous valuations on Tate rings.
Definition 2.8. Let A be a topological ring.
-
1. A is called Tate, if there is an open subring
 $A_0 \subset A$
together with an element
$A_0 \subset A$
together with an element
 $t \in A_0$
such that the topology on
$t \in A_0$
such that the topology on
 $A_0$
induced from A is t-adic and t becomes a unit in A.
$A_0$
induced from A is t-adic and t becomes a unit in A.
 $A_0$
is called a ring of definition and t is called a pseudouniformizer.
$A_0$
is called a ring of definition and t is called a pseudouniformizer. -
2. Let
 $A_0$
be a ring and
$A_0$
be a ring and
 $t \in A_0$
is a regular element. Then the Tate ring associated with
$t \in A_0$
is a regular element. Then the Tate ring associated with
 $(A_0,(t))$
Footnote
4
is the ring
$(A_0,(t))$
Footnote
4
is the ring
 $A:=A_{0}[\frac {1}{t}]$
equipped with the linear topology such that
$A:=A_{0}[\frac {1}{t}]$
equipped with the linear topology such that
 $\{t^{n}A_0\}_{n\geq 1}$
forms a fundamental system of open neighborhoods of
$\{t^{n}A_0\}_{n\geq 1}$
forms a fundamental system of open neighborhoods of
 $0\in A$
(it is a unique Tate ring containing
$0\in A$
(it is a unique Tate ring containing
 $A_{0}$
such that
$A_{0}$
such that
 $A_{0}$
is a ring of definition and t is a pseudouniformizer; see [Reference Nakazato and Shimomoto45, Lem. 2.11]).
$A_{0}$
is a ring of definition and t is a pseudouniformizer; see [Reference Nakazato and Shimomoto45, Lem. 2.11]).
For a Tate ring A, we denote by
![]() $A^{\circ } \subset A$
the subset consisting of power-bounded elements of A and by
$A^{\circ } \subset A$
the subset consisting of power-bounded elements of A and by
![]() $A^{\circ \circ } \subset A$
the subset consisting of topologically nilpotent elements of A. It is easy to verify that
$A^{\circ \circ } \subset A$
the subset consisting of topologically nilpotent elements of A. It is easy to verify that
![]() $A^{\circ \circ } \subset A^{\circ } \subset A$
,
$A^{\circ \circ } \subset A^{\circ } \subset A$
,
![]() $A^{\circ }$
is a subring of A and
$A^{\circ }$
is a subring of A and
![]() $A^{\circ \circ }$
is an ideal of
$A^{\circ \circ }$
is an ideal of
![]() $A^{\circ }$
. The pair
$A^{\circ }$
. The pair
![]() $(A,A^+)$
is called an affinoid Tate ring, if
$(A,A^+)$
is called an affinoid Tate ring, if
![]() $A^+ \subset A$
is an open and integrally closed subring contained in
$A^+ \subset A$
is an open and integrally closed subring contained in
![]() $A^{\circ }$
.Footnote
5
Let
$A^{\circ }$
.Footnote
5
Let
![]() $\operatorname {Spa}(A,A^+)$
denote the set of continuous valuations
$\operatorname {Spa}(A,A^+)$
denote the set of continuous valuations
![]() $|\cdot |$
on an affinoid Tate ring
$|\cdot |$
on an affinoid Tate ring
![]() $(A,A^+)$
satisfying an additional condition
$(A,A^+)$
satisfying an additional condition
![]() $|A^+|\le 1$
modulo a natural equivalence relation.
$|A^+|\le 1$
modulo a natural equivalence relation.
Let us pick an element
![]() $|\cdot | \in \operatorname {Spa}(A,A^+)$
, and set
$|\cdot | \in \operatorname {Spa}(A,A^+)$
, and set
![]() $\frak {p}:=\{x\in A^{+}~|~|x|=0\}$
. Then by Lemma 2.9,
$\frak {p}:=\{x\in A^{+}~|~|x|=0\}$
. Then by Lemma 2.9,
![]() $\frak {p}$
is a prime ideal, and
$\frak {p}$
is a prime ideal, and
![]() $|\cdot |$
defines a valuation ring
$|\cdot |$
defines a valuation ring
![]() $V_{|\cdot |} \subset \operatorname {Frac}(A^+/\frak {p})$
. This valuation ring is microbial attached to
$V_{|\cdot |} \subset \operatorname {Frac}(A^+/\frak {p})$
. This valuation ring is microbial attached to
![]() $|\cdot |$
in view of [Reference Bhatt8, Prop. 7.3.7]. For microbial valuation rings, we refer the reader to [Reference Huber33].
$|\cdot |$
in view of [Reference Bhatt8, Prop. 7.3.7]. For microbial valuation rings, we refer the reader to [Reference Huber33].
Lemma 2.9. Let
![]() $|\cdot |:A \to \Gamma \cup \{0\}$
be a semivaluation. Then
$|\cdot |:A \to \Gamma \cup \{0\}$
be a semivaluation. Then
![]() $\frak {p}:=\{x\in A~|~|x|=0\}$
is a prime ideal of A. Moreover,
$\frak {p}:=\{x\in A~|~|x|=0\}$
is a prime ideal of A. Moreover,
![]() $|\cdot |$
uniquely extends to a valuation
$|\cdot |$
uniquely extends to a valuation
![]() $|\cdot |_{\frak {p}}:\operatorname {Frac}(A/\frak {p}) \to \Gamma \cup \{0\}$
, and
$|\cdot |_{\frak {p}}:\operatorname {Frac}(A/\frak {p}) \to \Gamma \cup \{0\}$
, and
![]() $V_{|\cdot |}:=\{x \in \operatorname {Frac}(A/\mathfrak {p})~|~|x|_{\frak {p}}\le 1\}$
is a valuation ring with its field of fractions
$V_{|\cdot |}:=\{x \in \operatorname {Frac}(A/\mathfrak {p})~|~|x|_{\frak {p}}\le 1\}$
is a valuation ring with its field of fractions
![]() $\operatorname {Frac}(A/\frak {p})$
.
$\operatorname {Frac}(A/\frak {p})$
.
Proof. This is an easy exercise, using the properties stated in Definition 2.6.
The prime ideal
![]() $\frak {p}$
in Lemma 2.9 is called the support of the semivaluation
$\frak {p}$
in Lemma 2.9 is called the support of the semivaluation
![]() $|\cdot |$
.
$|\cdot |$
.
2.4 Perfectoid algebras
Let us recall the notion of perfectoid algebras over a perfectoid field as defined in [Reference Scholze52]. These are a special class of Banach algebras (see [Reference Nakazato and Shimomoto45, Sec. 2.4] for the definition of Banach rings in this context and how they are related to Tate rings).
Definition 2.10 (Perfectoid K-algebra)
Fix a perfectoid field K and let
![]() $\mathcal {A}$
be a Banach K-algebra. Then we say that
$\mathcal {A}$
be a Banach K-algebra. Then we say that
![]() $\mathcal {A}$
is a perfectoid K-algebra, if the following conditions hold:
$\mathcal {A}$
is a perfectoid K-algebra, if the following conditions hold:
-
1. The set of power-bounded elements
 $\mathcal {A}^{\circ } \subset \mathcal {A}$
is open and bounded.
$\mathcal {A}^{\circ } \subset \mathcal {A}$
is open and bounded. -
2. The Frobenius endomorphism on
 $\mathcal {A}^{\circ }/(p)$
is surjective.
$\mathcal {A}^{\circ }/(p)$
is surjective.
We will recall the almost variant of perfectoid algebras (see [Reference André1]).
Definition 2.11 (Almost perfectoid K-algebra)
Fix a perfectoid field K and let
![]() $\mathcal {A}$
be a Banach K-algebra with a basic setup
$\mathcal {A}$
be a Banach K-algebra with a basic setup
![]() $(\mathcal {A}^{\circ },I)$
. Then we say that
$(\mathcal {A}^{\circ },I)$
. Then we say that
![]() $\mathcal {A}$
is I-almost perfectoid, if the following conditions hold:
$\mathcal {A}$
is I-almost perfectoid, if the following conditions hold:
-
1. The set of power-bounded elements
 $\mathcal {A}^{\circ } \subset \mathcal {A}$
is open and bounded.
$\mathcal {A}^{\circ } \subset \mathcal {A}$
is open and bounded. -
2. The Frobenius endomorphism
 $Frob:\mathcal {A}^{\circ }/(p) \to \mathcal {A}^{\circ }/(p)$
is I-almost surjective.
$Frob:\mathcal {A}^{\circ }/(p) \to \mathcal {A}^{\circ }/(p)$
is I-almost surjective.
Example 2.12. Let
![]() $\mathcal {A}$
be a perfectoid K-algebra with a nonzero nonunit element
$\mathcal {A}$
be a perfectoid K-algebra with a nonzero nonunit element
![]() $t \in K^{\circ }$
admitting a compatible system of p-power roots
$t \in K^{\circ }$
admitting a compatible system of p-power roots
![]() $\{t^{\frac {1}{p^n}}\}_{n>0}$
. Fix any regular element
$\{t^{\frac {1}{p^n}}\}_{n>0}$
. Fix any regular element
![]() $g \in \mathcal {A}^{\circ }$
that admits a compatible system
$g \in \mathcal {A}^{\circ }$
that admits a compatible system
![]() $\{g^{\frac {1}{p^n}}\}_{n>0}$
. Let
$\{g^{\frac {1}{p^n}}\}_{n>0}$
. Let
![]() $I:=\bigcup _{n>0} (tg)^{\frac {1}{p^n}}$
. Then the pair
$I:=\bigcup _{n>0} (tg)^{\frac {1}{p^n}}$
. Then the pair
![]() $(\mathcal {A}^{\circ },I)$
gives a basic setup, which is a prototypical example that is encountered in this article.
$(\mathcal {A}^{\circ },I)$
gives a basic setup, which is a prototypical example that is encountered in this article.
3 Preliminary lemmas
3.1 Some properties of complete integral closure
Here, we investigate several properties of complete integral closure. First, we study how it behaves under separated completion. Thus, we start with recalling the following lemma, which is a key for the main results of [Reference Beauville and Laszlo6] (see also [61, Tag 0BNR] for a proof and related results).
Lemma 3.1 (Beauville–Laszlo)
Let A be a ring with a regular element
![]() $t\in A$
, and let
$t\in A$
, and let
![]() $\widehat {A}$
be the t-adic completion. Then t is a regular element in
$\widehat {A}$
be the t-adic completion. Then t is a regular element in
![]() $\widehat {A}$
and one has the commutative diagram:
$\widehat {A}$
and one has the commutative diagram:

that is Cartesian. In other words, we have
![]() $A \cong A[\frac {1}{t}] \times _{\widehat {A}[\frac {1}{t}]} \widehat {A}$
.
$A \cong A[\frac {1}{t}] \times _{\widehat {A}[\frac {1}{t}]} \widehat {A}$
.
Corollary 3.2. Let A be a Tate ring, and let
![]() $\mathcal {A}$
be the separated completion of A. Then the natural map
$\mathcal {A}$
be the separated completion of A. Then the natural map
![]() $\psi : A\to \mathcal {A}$
restricts to
$\psi : A\to \mathcal {A}$
restricts to
![]() $\psi ^{\circ }: A^{\circ }\to \mathcal {A}^{\circ }$
, and the commutative diagram:
$\psi ^{\circ }: A^{\circ }\to \mathcal {A}^{\circ }$
, and the commutative diagram:

is Cartesian.
Proof. Let
![]() $(A_{0}, (t))$
be a pair of definition of A, and
$(A_{0}, (t))$
be a pair of definition of A, and
![]() $\widehat {A_{0}}$
the t-adic completion of
$\widehat {A_{0}}$
the t-adic completion of
![]() $A_{0}$
. Then
$A_{0}$
. Then
![]() $\mathcal {A}$
is the Tate ring associated with
$\mathcal {A}$
is the Tate ring associated with
![]() $(\widehat {A_0}, (t))$
. Hence, the first assertion is clear. To check the second assertion, pick
$(\widehat {A_0}, (t))$
. Hence, the first assertion is clear. To check the second assertion, pick
![]() $a\in A$
such that
$a\in A$
such that
![]() $\psi (a)\in \mathcal {A}^{\circ }$
. Then there exists some
$\psi (a)\in \mathcal {A}^{\circ }$
. Then there exists some
![]() $l>0$
such that
$l>0$
such that
![]() $\psi (t^la^{n})=t^{l}\psi (a)^{n}\in \widehat {A_{0}}$
for every
$\psi (t^la^{n})=t^{l}\psi (a)^{n}\in \widehat {A_{0}}$
for every
![]() $n\geq 0$
. Hence
$n\geq 0$
. Hence
![]() $t^{l}a^{n}\in A_{0}$
for every
$t^{l}a^{n}\in A_{0}$
for every
![]() $n\geq 0$
by Lemma 3.1. Therefore,
$n\geq 0$
by Lemma 3.1. Therefore,
![]() $a\in A^{\circ }$
as desired.
$a\in A^{\circ }$
as desired.
The following lemma is quite useful and often used in basic theory of perfectoid spaces. We take a copy from Bhatt’s lecture notes [Reference Bhatt8].
Lemma 3.3. Let A be a ring with a regular element
![]() $t \in A$
, and let
$t \in A$
, and let
![]() $\widehat {A}$
be the t-adic completion of A. Fix a prime number
$\widehat {A}$
be the t-adic completion of A. Fix a prime number
![]() $p>0$
. Then the following assertions hold:
$p>0$
. Then the following assertions hold:
-
1. Suppose that A is integrally closed in
 $A[\frac {1}{t}]$
. Then
$A[\frac {1}{t}]$
. Then
 $\widehat {A}$
is integrally closed in
$\widehat {A}$
is integrally closed in
 $\widehat {A}[\frac {1}{t}]$
. If moreover A admits a compatible system of p-power roots
$\widehat {A}[\frac {1}{t}]$
. If moreover A admits a compatible system of p-power roots
 $\{t^{\frac {1}{p^n}}\}_{n>0}$
, then
$\{t^{\frac {1}{p^n}}\}_{n>0}$
, then
 $t^{-\frac {1}{p^{\infty }}} A$
is integrally closed in
$t^{-\frac {1}{p^{\infty }}} A$
is integrally closed in
 $A[\frac {1}{t}]$
.
$A[\frac {1}{t}]$
. -
2. Suppose that A is completely integrally closed in
 $A[\frac {1}{t}]$
. Then
$A[\frac {1}{t}]$
. Then
 $\widehat {A}$
is completely integrally closed in
$\widehat {A}$
is completely integrally closed in
 $\widehat {A}[\frac {1}{t}]$
. If moreover A admits a compatible system of p-power roots
$\widehat {A}[\frac {1}{t}]$
. If moreover A admits a compatible system of p-power roots
 $\{t^{\frac {1}{p^n}}\}_{n>0}$
, then
$\{t^{\frac {1}{p^n}}\}_{n>0}$
, then
 $t^{-\frac {1}{p^{\infty }}} A$
is completely integrally closed in
$t^{-\frac {1}{p^{\infty }}} A$
is completely integrally closed in
 $A[\frac {1}{t}]$
.
$A[\frac {1}{t}]$
.
Proof. We refer the reader to [Reference Bhatt8, Lem. 5.1.1–5.1.3] and [Reference Nakazato and Shimomoto45, Lem. 2.7]. Here, we point out that Lemma 3.1 plays a role in the proofs.
The following lemma is easy to prove, but plays an important role in our arguments.
Lemma 3.4. Let A be a ring, and let
![]() $t \in A$
be a regular element. Fix a prime number
$t \in A$
be a regular element. Fix a prime number
![]() $p>0$
. Suppose that A admits a compatible system of p-power roots
$p>0$
. Suppose that A admits a compatible system of p-power roots
![]() $\{t^{\frac {1}{p^n}}\}_{n>0}$
. Then for any
$\{t^{\frac {1}{p^n}}\}_{n>0}$
. Then for any
![]() $A[\frac {1}{t}]$
-algebra B, we have
$A[\frac {1}{t}]$
-algebra B, we have
![]() $A^{*}_{B} = (t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}$
.
$A^{*}_{B} = (t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}$
.
Proof. It suffices to show that
![]() $(t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}\subset A^{*}_{B}$
. Let
$(t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}\subset A^{*}_{B}$
. Let
![]() $A'$
be the image of A in B. Then the image of
$A'$
be the image of A in B. Then the image of
![]() $t^{-\frac {1}{p^{\infty }}}A$
in B is contained in
$t^{-\frac {1}{p^{\infty }}}A$
in B is contained in
![]() $t^{-\frac {1}{p^{\infty }}}A'$
. Thus, we have
$t^{-\frac {1}{p^{\infty }}}A'$
. Thus, we have
![]() $(t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}\subset (t^{-\frac {1}{p^{\infty }}}A')^{*}_{B}$
and
$(t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}\subset (t^{-\frac {1}{p^{\infty }}}A')^{*}_{B}$
and
![]() $A^*_{B}=(A')^{*}_{B}$
. Hence, we may assume that
$A^*_{B}=(A')^{*}_{B}$
. Hence, we may assume that
![]() $A=A'$
, that is,
$A=A'$
, that is,
![]() $A[\frac {1}{t}]$
is a subring of B. Pick
$A[\frac {1}{t}]$
is a subring of B. Pick
![]() $x\in (t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}$
. Then,
$x\in (t^{-\frac {1}{p^{\infty }}}A)^{*}_{B}$
. Then,
![]() $\sum ^{\infty }_{n=0}t^{-\frac {1}{p^{\infty }}}A\cdot x^{n}$
is contained in a finitely generated
$\sum ^{\infty }_{n=0}t^{-\frac {1}{p^{\infty }}}A\cdot x^{n}$
is contained in a finitely generated
![]() $t^{-\frac {1}{p^{\infty }}} A$
-submodule of B, and thus so is
$t^{-\frac {1}{p^{\infty }}} A$
-submodule of B, and thus so is
![]() $\sum _{n=0}^{\infty } A\cdot x^{n}$
. Hence
$\sum _{n=0}^{\infty } A\cdot x^{n}$
. Hence
![]() $t\sum ^{\infty }_{n=0}A \cdot x^{n}$
is contained in a finitely generated A-submodule M of B. Let
$t\sum ^{\infty }_{n=0}A \cdot x^{n}$
is contained in a finitely generated A-submodule M of B. Let
![]() $b_{1},\ldots , b_{r}$
be a system of generators of M over A. Then, since t is invertible in B, we obtain a finitely generated A-submodule
$b_{1},\ldots , b_{r}$
be a system of generators of M over A. Then, since t is invertible in B, we obtain a finitely generated A-submodule
![]() $\sum ^{r}_{i=1}A\cdot \frac {b_{i}}{t}$
of B, which contains
$\sum ^{r}_{i=1}A\cdot \frac {b_{i}}{t}$
of B, which contains
![]() $\sum ^{\infty }_{n=0}A\cdot x^{n}$
, as desired.
$\sum ^{\infty }_{n=0}A\cdot x^{n}$
, as desired.
The following corollary is an immediate consequence of Lemma 3.4.
Corollary 3.5. Let A be a ring with a regular element
![]() $t \in A$
such that A is completely integrally closed in
$t \in A$
such that A is completely integrally closed in
![]() $A[\frac {1}{t}]$
. Fix a prime number
$A[\frac {1}{t}]$
. Fix a prime number
![]() $p>0$
. Suppose that A admits a compatible system of p-power roots
$p>0$
. Suppose that A admits a compatible system of p-power roots
![]() $\{t^{\frac {1}{p^n}}\}_{n>0}$
. Then we have
$\{t^{\frac {1}{p^n}}\}_{n>0}$
. Then we have
![]() $t^{-\frac {1}{p^{\infty }}} A=A$
(in particular,
$t^{-\frac {1}{p^{\infty }}} A=A$
(in particular,
![]() $t^{-\frac {1}{p^{\infty }}} A$
is completely integrally closed in
$t^{-\frac {1}{p^{\infty }}} A$
is completely integrally closed in
![]() $A[\frac {1}{t}]$
).
$A[\frac {1}{t}]$
).
Now, let us discuss complete integral closedness of inverse limits.
Lemma 3.6. Let A be a ring with an element
![]() $t\in A$
, let
$t\in A$
, let
![]() $\Lambda $
be a directed poset, and let
$\Lambda $
be a directed poset, and let
![]() $\{A_{\lambda }\}_{\lambda \in \Lambda }$
an inverse system of A-algebras. Suppose that each
$\{A_{\lambda }\}_{\lambda \in \Lambda }$
an inverse system of A-algebras. Suppose that each
![]() $A_{\lambda }$
is t-torsion-free and completely integrally closed in
$A_{\lambda }$
is t-torsion-free and completely integrally closed in
![]() $A_{\lambda }[\frac {1}{t}]$
. Then
$A_{\lambda }[\frac {1}{t}]$
. Then
![]() $\varprojlim _{\lambda } A_{\lambda }$
is a t-torsion-free A-algebra and completely integrally closed in
$\varprojlim _{\lambda } A_{\lambda }$
is a t-torsion-free A-algebra and completely integrally closed in
![]() $(\varprojlim _{\lambda } A_{\lambda })[\frac {1}{t}]$
.
$(\varprojlim _{\lambda } A_{\lambda })[\frac {1}{t}]$
.
Proof. Clearly,
![]() $\varprojlim _{\lambda } A_{\lambda }$
is a t-torsion-free A-algebra. Pick an element
$\varprojlim _{\lambda } A_{\lambda }$
is a t-torsion-free A-algebra. Pick an element
![]() $b\in (\varprojlim _{\lambda } A_{\lambda })[\frac {1}{t}]$
which is almost integral over
$b\in (\varprojlim _{\lambda } A_{\lambda })[\frac {1}{t}]$
which is almost integral over
![]() $\varprojlim _{\lambda } A_{\lambda }$
. Then there exists some
$\varprojlim _{\lambda } A_{\lambda }$
. Then there exists some
![]() $m>0$
such that
$m>0$
such that
![]() $t^{m}b^{n}\in \varprojlim _{\lambda } A_{\lambda }$
for every
$t^{m}b^{n}\in \varprojlim _{\lambda } A_{\lambda }$
for every
![]() $n>0$
. Take
$n>0$
. Take
![]() $d>0$
and
$d>0$
and
![]() $a=(a_{\lambda })\in \varprojlim _{\lambda } A_{\lambda }$
for which
$a=(a_{\lambda })\in \varprojlim _{\lambda } A_{\lambda }$
for which
![]() $t^{d}b=a$
. Then for every
$t^{d}b=a$
. Then for every
![]() $n>0$
, it follows that
$n>0$
, it follows that
![]() $t^{dn+m}b^{n}=t^{m}a^{n}$
, which implies
$t^{dn+m}b^{n}=t^{m}a^{n}$
, which implies
![]() $t^{m}a^{n}\in t^{dn}(\varprojlim _{\lambda } A_{\lambda })$
. Thus for each
$t^{m}a^{n}\in t^{dn}(\varprojlim _{\lambda } A_{\lambda })$
. Thus for each
![]() $\lambda \in \Lambda $
, the element
$\lambda \in \Lambda $
, the element
![]() $\frac {a_{\lambda }}{t^{d}}\in A_{\lambda }[\frac {1}{t}]$
satisfies
$\frac {a_{\lambda }}{t^{d}}\in A_{\lambda }[\frac {1}{t}]$
satisfies
![]() $t^{m}(\frac {a_{\lambda }}{t^{d}})^{n}\in A_{\lambda }$
for every n. Since
$t^{m}(\frac {a_{\lambda }}{t^{d}})^{n}\in A_{\lambda }$
for every n. Since
![]() $A_{\lambda }$
is completely integrally closed in
$A_{\lambda }$
is completely integrally closed in
![]() $A_{\lambda }[\frac {1}{t}]$
, one finds that
$A_{\lambda }[\frac {1}{t}]$
, one finds that
![]() $a_{\lambda }\in t^{d}A_{\lambda }\ (\forall \lambda \in \Lambda )$
and thus
$a_{\lambda }\in t^{d}A_{\lambda }\ (\forall \lambda \in \Lambda )$
and thus
![]() $a\in t^{d}(\varprojlim _{\lambda } A_{\lambda })$
. Hence
$a\in t^{d}(\varprojlim _{\lambda } A_{\lambda })$
. Hence
![]() $b=\frac {a}{t^d} \in \varprojlim _{\lambda }A_{\lambda }$
, as desired.
$b=\frac {a}{t^d} \in \varprojlim _{\lambda }A_{\lambda }$
, as desired.
In the situation of Lemma 2.1, complete integral closedness is preserved under
![]() $(~)_*$
.
$(~)_*$
.
Lemma 3.7. Let
![]() $A \hookrightarrow B$
be a ring extension such that A is completely integrally closed in B. Suppose that A has an element t such that B is t-torsion-free and A admits a compatible system of p-power roots
$A \hookrightarrow B$
be a ring extension such that A is completely integrally closed in B. Suppose that A has an element t such that B is t-torsion-free and A admits a compatible system of p-power roots
![]() $\{t^{\frac {1}{p^{n}}}\}_{n>0}$
. Then
$\{t^{\frac {1}{p^{n}}}\}_{n>0}$
. Then
![]() $t^{-\frac {1}{p^{\infty }}}A$
is completely integrally closed in
$t^{-\frac {1}{p^{\infty }}}A$
is completely integrally closed in
![]() $t^{-\frac {1}{p^{\infty }}}B$
.
$t^{-\frac {1}{p^{\infty }}}B$
.
Proof. Pick an element
![]() $c\in t^{-\frac {1}{p^{\infty }}}B$
which is almost integral over
$c\in t^{-\frac {1}{p^{\infty }}}B$
which is almost integral over
![]() $t^{-\frac {1}{p^{\infty }}}A$
. We would like to show that
$t^{-\frac {1}{p^{\infty }}}A$
. We would like to show that
![]() $t^{\frac {1}{p^{k}}}c\ \in A$
for every
$t^{\frac {1}{p^{k}}}c\ \in A$
for every
![]() $k>0$
. Since A is completely integrally closed in B, it suffices to check that each
$k>0$
. Since A is completely integrally closed in B, it suffices to check that each
![]() $t^{\frac {1}{p^{k}}}c\in B$
is almost integral over A. Now by assumption,
$t^{\frac {1}{p^{k}}}c\in B$
is almost integral over A. Now by assumption,
![]() $\sum ^{\infty }_{n=0}t^{-\frac {1}{p^{\infty }}}A\cdot c^{n}$
is contained in a finitely generated
$\sum ^{\infty }_{n=0}t^{-\frac {1}{p^{\infty }}}A\cdot c^{n}$
is contained in a finitely generated
![]() $t^{-\frac {1}{p^{\infty }}}A$
-submodule of
$t^{-\frac {1}{p^{\infty }}}A$
-submodule of
![]() $t^{-\frac {1}{p^{\infty }}}B$
. Hence,
$t^{-\frac {1}{p^{\infty }}}B$
. Hence,
![]() $t^{\frac {1}{p^{k}}}(\sum ^{\infty }_{n=0}t^{-\frac {1}{p^{\infty }}}A\cdot c^{n})$
is contained in a finitely generated A-submodule of B for every
$t^{\frac {1}{p^{k}}}(\sum ^{\infty }_{n=0}t^{-\frac {1}{p^{\infty }}}A\cdot c^{n})$
is contained in a finitely generated A-submodule of B for every
![]() $k>0$
. Meanwhile, it follows that
$k>0$
. Meanwhile, it follows that
 $$ \begin{align*}\sum^{\infty}_{n=0} A\cdot (t^{\frac{1}{p^{k}}}c)^n \subset t^{\frac{1}{p^{k}}}\biggl(\sum^{\infty}_{n=0}A\cdot c^{n}\biggr) \subset t^{\frac{1}{p^{k}}}\biggl(\sum^{\infty}_{n=0}t^{-\frac{1}{p^{\infty}}}A\cdot c^{n}\biggr). \end{align*} $$
$$ \begin{align*}\sum^{\infty}_{n=0} A\cdot (t^{\frac{1}{p^{k}}}c)^n \subset t^{\frac{1}{p^{k}}}\biggl(\sum^{\infty}_{n=0}A\cdot c^{n}\biggr) \subset t^{\frac{1}{p^{k}}}\biggl(\sum^{\infty}_{n=0}t^{-\frac{1}{p^{\infty}}}A\cdot c^{n}\biggr). \end{align*} $$
Therefore,
![]() $t^{\frac {1}{p^{k}}}c\in B$
is almost integral over A, as desired.
$t^{\frac {1}{p^{k}}}c\in B$
is almost integral over A, as desired.
Next, we consider several types of ring extensions. The following lemmas are mainly used in §6.
Lemma 3.8. The following assertions hold:
-
1. Let R be a Noetherian integrally closed domain with its absolute integral closure
 $R^+$
and assume that A is a ring such that
$R^+$
and assume that A is a ring such that
 $R \subset A \subset R^+$
. Then A is integrally closed in
$R \subset A \subset R^+$
. Then A is integrally closed in
 $\operatorname {Frac}(A)$
if and only if A is completely integrally closed in
$\operatorname {Frac}(A)$
if and only if A is completely integrally closed in
 $\operatorname {Frac}(A)$
.
$\operatorname {Frac}(A)$
. -
2. Let
 $R \subset S \subset T$
be ring extensions. Assume that R is completely integrally closed in T. Then R is also completely integrally closed in S.
$R \subset S \subset T$
be ring extensions. Assume that R is completely integrally closed in T. Then R is also completely integrally closed in S.
Proof. (1): The proof is found in the proof of [Reference Shimomoto55, Th. 5.9], whose statement is given only for Noetherian normal rings of characteristic
![]() $p>0$
. However, the argument there remains valid for Noetherian normal rings of arbitrary characteristic (see also Proposition 7.1).
$p>0$
. However, the argument there remains valid for Noetherian normal rings of arbitrary characteristic (see also Proposition 7.1).
(2): For
![]() $s \in S$
, assume that
$s \in S$
, assume that
![]() $\sum _{n=0}^{\infty } R \cdot s^n$
is contained in a finitely generated R-submodule of S. Then this property remains true when regarded as an R-submodule of T. So we have
$\sum _{n=0}^{\infty } R \cdot s^n$
is contained in a finitely generated R-submodule of S. Then this property remains true when regarded as an R-submodule of T. So we have
![]() $s \in R$
by our assumption.
$s \in R$
by our assumption.
Lemma 3.9. Let A be a normal domain with field of fractions
![]() $\operatorname {Frac}(A)$
and assume that
$\operatorname {Frac}(A)$
and assume that
![]() $\operatorname {Frac}(A) \hookrightarrow B$
is an integral extension such that B is reduced. Denote by
$\operatorname {Frac}(A) \hookrightarrow B$
is an integral extension such that B is reduced. Denote by
![]() $C:=A^+_B$
the integral closure of A in B. Then
$C:=A^+_B$
the integral closure of A in B. Then
![]() $C_{\frak {p}}$
is a normal domain for any prime ideal
$C_{\frak {p}}$
is a normal domain for any prime ideal
![]() $\frak {p}$
of C.
$\frak {p}$
of C.
Proof. Notice that B can be written as the filtered colimit of finite integral subextensions
![]() $\operatorname {Frac}(A) \to B' \to B$
. Without loss of generality, we may assume and do that
$\operatorname {Frac}(A) \to B' \to B$
. Without loss of generality, we may assume and do that
![]() $\operatorname {Frac}(A) \to B$
is a finite integral extension. Since
$\operatorname {Frac}(A) \to B$
is a finite integral extension. Since
![]() $\operatorname {Frac}(A)$
is a field, B is a reduced Artinian ring, so that we can write
$\operatorname {Frac}(A)$
is a field, B is a reduced Artinian ring, so that we can write
![]() $B=\Pi _{i=1}^m L_i$
with
$B=\Pi _{i=1}^m L_i$
with
![]() $L_i$
being a field. Since
$L_i$
being a field. Since
![]() $A \to C$
is torsion-free and integral, we see that
$A \to C$
is torsion-free and integral, we see that
![]() $\operatorname {Frac}(A) \otimes _A C$
is the total ring of fractions of C, which is just B. In other words, C has finitely many minimal prime ideals, because so does B. Then by [61, Tag 030C], C is a finite product of normal domains, which shows that
$\operatorname {Frac}(A) \otimes _A C$
is the total ring of fractions of C, which is just B. In other words, C has finitely many minimal prime ideals, because so does B. Then by [61, Tag 030C], C is a finite product of normal domains, which shows that
![]() $C_{\frak {p}}$
is a normal domain for any prime ideal
$C_{\frak {p}}$
is a normal domain for any prime ideal
![]() $\frak {p} \subset C$
.
$\frak {p} \subset C$
.
3.2 Almost regular sequences and the ring of bounded functions
The notion of almost regular sequences often shows up in the main content of this article.
Definition 3.10 (Almost regular sequence)
Let
![]() $(A,I)$
be a basic setup with a sequence of elements
$(A,I)$
be a basic setup with a sequence of elements
![]() $x_1,\ldots ,x_n$
in A, and let M be an A-module. Then we say that
$x_1,\ldots ,x_n$
in A, and let M be an A-module. Then we say that
![]() $x_1,\ldots ,x_n$
is an I-almost regular sequence in M if
$x_1,\ldots ,x_n$
is an I-almost regular sequence in M if
for any
![]() $b \in I$
and
$b \in I$
and
![]() $i=0,\ldots ,n-1$
. In particular, we say that an element
$i=0,\ldots ,n-1$
. In particular, we say that an element
![]() $x \in M$
is I-almost regular if the kernel of the multiplication map
$x \in M$
is I-almost regular if the kernel of the multiplication map
![]() $M \xrightarrow {x} M$
is annihilated by I.
$M \xrightarrow {x} M$
is annihilated by I.
First of all, we record the following fundamental lemma.
Lemma 3.11. Let
![]() $(A,I)$
be a basic setup and assume that
$(A,I)$
be a basic setup and assume that
![]() $a,b$
is an I-almost regular sequence on A. Let
$a,b$
is an I-almost regular sequence on A. Let
![]() $\widehat {A}$
denote the a-adic completion of A. Then a and b are I-almost regular elements of
$\widehat {A}$
denote the a-adic completion of A. Then a and b are I-almost regular elements of
![]() $\widehat {A}$
.
$\widehat {A}$
.
Proof. First, we prove that a is I-almost regular on
![]() $\widehat {A}$
. For any
$\widehat {A}$
. For any
![]() $k>0$
, the multiplication map
$k>0$
, the multiplication map
![]() $A \xrightarrow {a} A$
induces an I-almost injective map
$A \xrightarrow {a} A$
induces an I-almost injective map
![]() $A/(a^k) \xrightarrow {a} A/(a^{k+1})$
. This forms a commutative diagram:
$A/(a^k) \xrightarrow {a} A/(a^{k+1})$
. This forms a commutative diagram:

Taking inverse limits along the vertical directions, respectively,
![]() $\widehat {A} \xrightarrow {a} \widehat {A}$
is I-almost injective.
$\widehat {A} \xrightarrow {a} \widehat {A}$
is I-almost injective.
Next, we prove that b is I-almost regular. Let
![]() $t \in \widehat {A}$
be such that
$t \in \widehat {A}$
be such that
![]() $bt=0$
. Then one obviously has
$bt=0$
. Then one obviously has
![]() $bt \in a^n \widehat {A}$
for all
$bt \in a^n \widehat {A}$
for all
![]() $n>0$
. Since b is I-almost regular on
$n>0$
. Since b is I-almost regular on
![]() $A/(a^n) \cong \widehat {A}/(a^n)$
, it follows that
$A/(a^n) \cong \widehat {A}/(a^n)$
, it follows that
![]() $\epsilon t \in \bigcap _{n>0} a^n \widehat {A}=0$
for any
$\epsilon t \in \bigcap _{n>0} a^n \widehat {A}=0$
for any
![]() $\epsilon \in I$
.
$\epsilon \in I$
.
Example 3.12. We give a counterexample to Lemma 3.11 without almost regularity condition. Let us consider the subring:
Then it is clear that R is a domain. However, after taking the p-adic completion
![]() $\widehat {R}$
, since
$\widehat {R}$
, since
![]() $x \in p^nR$
, x becomes zero in
$x \in p^nR$
, x becomes zero in
![]() $\widehat {R}$
. Therefore, p is a regular element in
$\widehat {R}$
. Therefore, p is a regular element in
![]() $\widehat {R}$
, while x is not so.
$\widehat {R}$
, while x is not so.
Let A be a ring with elements
![]() $f,g \in A$
. Then we can consider the ring of bounded functions defined by a sequence
$f,g \in A$
. Then we can consider the ring of bounded functions defined by a sequence
![]() $f^n,g$
, denoted by
$f^n,g$
, denoted by
![]() $A[\frac {f^n}{g}]$
as a subring of
$A[\frac {f^n}{g}]$
as a subring of
![]() $A[\frac {1}{g}]$
. In other words, we define
$A[\frac {1}{g}]$
. In other words, we define
 $$ \begin{align*}A[\frac{f^n}{g}]:=\big(A[T]/(gT-f^n)\big)\big/\frak{a}, \end{align*} $$
$$ \begin{align*}A[\frac{f^n}{g}]:=\big(A[T]/(gT-f^n)\big)\big/\frak{a}, \end{align*} $$
where
![]() $\frak {a}:=\bigcup _{m>0} (0: g^m)$
as an ideal of
$\frak {a}:=\bigcup _{m>0} (0: g^m)$
as an ideal of
![]() $A[T]/(gT-f^n)$
. In the technical part of this article, the following problem plays a central role.
$A[T]/(gT-f^n)$
. In the technical part of this article, the following problem plays a central role.
Problem 1 (Algebraic formulation of Riemann’s extension problem)
Study the ring-theoretic structure of the intersection
 $$ \begin{align*}\bigcap_{n>0} \biggl(A[\frac{f^n}{g}]\biggr)^{*}_{A[\frac{1}{fg}]} \end{align*} $$
$$ \begin{align*}\bigcap_{n>0} \biggl(A[\frac{f^n}{g}]\biggr)^{*}_{A[\frac{1}{fg}]} \end{align*} $$
taken inside
![]() $A[\frac {1}{fg}]$
.
$A[\frac {1}{fg}]$
.
In his remarkable article [Reference Scholze53], Scholze studied the perfectoid version of Problem 1, with an application to the construction of Galois representations using torsion classes in the cohomology of certain symmetric spaces. We need the following fact on the description of the ring of bounded functions as a Rees algebra. In the case that the relevant sequence is regular, the proof is found in [61, Tag 0BIQ].
Lemma 3.13. Let
![]() $(A,I)$
be a basic setup, and let
$(A,I)$
be a basic setup, and let
![]() $f, g \in A$
be elements such that
$f, g \in A$
be elements such that
![]() $f,g$
forms an I-almost regular sequence. Then the ring map
$f,g$
forms an I-almost regular sequence. Then the ring map
 $$ \begin{align*}A[T]/(gT-f) \to A[\frac{f}{g}];~T \mapsto \dfrac{f}{g} \end{align*} $$
$$ \begin{align*}A[T]/(gT-f) \to A[\frac{f}{g}];~T \mapsto \dfrac{f}{g} \end{align*} $$
is an I-almost isomorphism.
Proof. It suffices to prove that
![]() $A[T]/(gT-f)$
is I-almost g-torsion-free. So suppose that
$A[T]/(gT-f)$
is I-almost g-torsion-free. So suppose that
for some
![]() $a \in A[T]$
and some
$a \in A[T]$
and some
![]() $k \in \mathbb {N}$
. Let
$k \in \mathbb {N}$
. Let
![]() $\epsilon \in I$
be any element. Then we want to show that
$\epsilon \in I$
be any element. Then we want to show that
![]() $\epsilon a \in (gT-f)$
. Now, we can find
$\epsilon a \in (gT-f)$
. Now, we can find
![]() $b \in A[T]$
such that
$b \in A[T]$
such that
![]() $g^ka=(gT-f)b$
and write this equation as
$g^ka=(gT-f)b$
and write this equation as
By the almost regularity of
![]() $f,g$
on
$f,g$
on
![]() $A[T]$
, for any
$A[T]$
, for any
![]() $\epsilon _{n_1} \in I$
, it follows that
$\epsilon _{n_1} \in I$
, it follows that
![]() $\epsilon _{n_1}(bT-g^{k-1}a)=fc$
for some
$\epsilon _{n_1}(bT-g^{k-1}a)=fc$
for some
![]() $c \in A[T]$
. Substituting this back into (3.2), we have
$c \in A[T]$
. Substituting this back into (3.2), we have
![]() $\epsilon _{n_1} bf=gfc$
. As f is I-almost regular, we have
$\epsilon _{n_1} bf=gfc$
. As f is I-almost regular, we have
![]() $\epsilon _{n_1}\epsilon _{n_2} b=\epsilon _{n_2}gc$
for any
$\epsilon _{n_1}\epsilon _{n_2} b=\epsilon _{n_2}gc$
for any
![]() $\epsilon _{n_2} \in I$
. Since
$\epsilon _{n_2} \in I$
. Since
![]() $\epsilon _{n_1}\epsilon _{n_2}g^{k-1}a=\epsilon _{n_1}\epsilon _{n_2} bT-\epsilon _{n_2} fc$
, we obtain
$\epsilon _{n_1}\epsilon _{n_2}g^{k-1}a=\epsilon _{n_1}\epsilon _{n_2} bT-\epsilon _{n_2} fc$
, we obtain
![]() $\epsilon _{n_1}\epsilon _{n_2}g^{k-1}a=\epsilon _{n_2}c(gT-f)$
. Since
$\epsilon _{n_1}\epsilon _{n_2}g^{k-1}a=\epsilon _{n_2}c(gT-f)$
. Since
![]() $\epsilon _{n_1},\epsilon _{n_2} \in I$
are arbitrary and
$\epsilon _{n_1},\epsilon _{n_2} \in I$
are arbitrary and
![]() $I=I^2$
, we find that
$I=I^2$
, we find that
![]() $\epsilon g^{k-1}a \in (gT-f)$
for any
$\epsilon g^{k-1}a \in (gT-f)$
for any
![]() $\epsilon \in I$
. Arguing inductively on k in view of (3.1), it follows that
$\epsilon \in I$
. Arguing inductively on k in view of (3.1), it follows that
![]() $\epsilon a \in (gT-f)$
for any
$\epsilon a \in (gT-f)$
for any
![]() $\epsilon \in I$
, as desired.
$\epsilon \in I$
, as desired.
We prove a result which compares the ring of bounded functions under completion. This result will play a crucial role later.
Proposition 3.14. Let the notation and the hypotheses be as in Lemma 3.13. Then for any
![]() $n \ge 0$
, there is an I-almost isomorphism of rings:
$n \ge 0$
, there is an I-almost isomorphism of rings:
 $$ \begin{align*}\widehat{A[\dfrac{f^n}{g}]} \xrightarrow{\approx} \widehat{\widehat{A}[\frac{f^n}{g}]}, \end{align*} $$
$$ \begin{align*}\widehat{A[\dfrac{f^n}{g}]} \xrightarrow{\approx} \widehat{\widehat{A}[\frac{f^n}{g}]}, \end{align*} $$
where
![]() $\widehat {(~)}$
is the f-adic completion.
$\widehat {(~)}$
is the f-adic completion.
Proof. In view of Lemma 3.13, we need to show that the natural map
is bijective. It suffices to show that for any
![]() $n>0$
, (3.3) is bijective after dividing out by the ideal generated by
$n>0$
, (3.3) is bijective after dividing out by the ideal generated by
![]() $f^n$
on both sides. So we get
$f^n$
on both sides. So we get
which is isomorphic to
Since
![]() $A/(f^n) \cong \widehat {A}/(f^n)$
, we are done.
$A/(f^n) \cong \widehat {A}/(f^n)$
, we are done.
4 Finite étale extensions of Tate rings
Here, we study some behavior of finite étale extensions of Tate rings under rational localization.
4.1 Finite étale extensions of preuniform Tate rings
Let us begin with a review on some results in [Reference Nakazato and Shimomoto45] used later. First, we recall a canonical structure as a Tate ring that is induced on a module-finite algebra over a Tate ring (see [Reference Nakazato and Shimomoto45, Lem. 2.19 and 2.20] for the next lemma).
Lemma 4.1. Let A be a Tate ring, and let B be a module-finite A-algebra. Take a ring of definition
![]() $A_0\subset A$
, a pseudouniformizer
$A_0\subset A$
, a pseudouniformizer
![]() $t\in A_0$
and a finite generating set S of B over A. Let
$t\in A_0$
and a finite generating set S of B over A. Let
![]() $M_0\subset B$
be the
$M_0\subset B$
be the
![]() $A_0$
-submodule generated by S. Equip B with the linear topology defined by
$A_0$
-submodule generated by S. Equip B with the linear topology defined by
![]() $\{t^nM_0\}_{n>0}$
. Then the following assertions hold:
$\{t^nM_0\}_{n>0}$
. Then the following assertions hold:
-
1. The topology on B is independent of the choices of
 $A_0$
, t and S.
$A_0$
, t and S. -
2. B is a Tate ring with the following property:
-
• for every ring of definition
 $A_0$
and every pseudouniformizer
$A_0$
and every pseudouniformizer
 $t\in A_0$
of A, there exists a ring of definition
$t\in A_0$
of A, there exists a ring of definition
 $B_0$
of B that is an integral
$B_0$
of B that is an integral
 $A_0$
-subalgebra of B with finitely many generators and
$A_0$
-subalgebra of B with finitely many generators and
 $t\in B_0$
is a pseudouniformizer of B.
$t\in B_0$
is a pseudouniformizer of B.
-
Next, we recall the definition of (pre)uniformity of Tate rings.
Definition 4.2. Let A be a Tate ring. We say that A is preuniform if
![]() $A^{\circ }$
is a ring of definition of A. Moreover, we say that A is uniform if A is preuniform and complete and separated.
$A^{\circ }$
is a ring of definition of A. Moreover, we say that A is uniform if A is preuniform and complete and separated.
Permanence of (pre)uniformity is one of the most remarkable features of finite étale extensions of Tate rings (see [Reference Nakazato and Shimomoto45, Cor. 4.8(1), (4), and (5)] for the next proposition).
Proposition 4.3. Let A be a preuniform Tate ring. Let
![]() $f: A\to B$
be a finite étale ring map. Equip B with the canonical structure as a Tate ring (cf. Lemma 4.1). Then the following assertions hold:
$f: A\to B$
be a finite étale ring map. Equip B with the canonical structure as a Tate ring (cf. Lemma 4.1). Then the following assertions hold:
-
1. B is also preuniform. In particular, for any ring of definition
 $A_0$
of A,
$A_0$
of A,
 $(A_0)^+_B$
and
$(A_0)^+_B$
and
 $(A_0)^*_B$
are rings of definition of B.
$(A_0)^*_B$
are rings of definition of B. -
2. If f is injective, then
 $f^{-1}(B^{\circ })=A^{\circ }$
.
$f^{-1}(B^{\circ })=A^{\circ }$
. -
3. If A is uniform, then so is B.
When one considers separated completion of finite étale extensions of Tate rings, two types of extension of complete Tate rings appear. The following statement assures that they are isomorphic under the preuniformity assumption (see [Reference Nakazato and Shimomoto45, Cor. 4.10] for the next proposition).
Proposition 4.4. Let A be a preuniform Tate ring with a pseudouniformizer t. Let
![]() $\mathcal {A}$
be the separated completion of A. Let B be a finite étale A-algebra and denote by
$\mathcal {A}$
be the separated completion of A. Let B be a finite étale A-algebra and denote by
![]() $\mathcal {B}$
the finite étale
$\mathcal {B}$
the finite étale
![]() $\mathcal {A}$
-algebra
$\mathcal {A}$
-algebra
![]() $B\otimes _A\mathcal {A}$
. Equip B and
$B\otimes _A\mathcal {A}$
. Equip B and
![]() $\mathcal {B}$
with the canonical structure as a Tate ring (cf. Lemma 4.1), respectively. Let
$\mathcal {B}$
with the canonical structure as a Tate ring (cf. Lemma 4.1), respectively. Let
![]() $\widehat {B^{\circ }}$
be the t-adic completion of
$\widehat {B^{\circ }}$
be the t-adic completion of
![]() $B^{\circ }$
. Then the natural A-algebra homomorphism
$B^{\circ }$
. Then the natural A-algebra homomorphism
![]() $\varphi : \mathcal {B}\rightarrow \widehat {B^{\circ }}[\frac {1}{t}]$
is an isomorphism which induces an isomorphism
$\varphi : \mathcal {B}\rightarrow \widehat {B^{\circ }}[\frac {1}{t}]$
is an isomorphism which induces an isomorphism
![]() $\mathcal {B}^{\circ }\xrightarrow {\cong }\widehat {B^{\circ }}$
.
$\mathcal {B}^{\circ }\xrightarrow {\cong }\widehat {B^{\circ }}$
.
In addition, we record a complement to §3.1. Preuniform Tate rings fit into Galois theory of rings.
Lemma 4.5. Let A be a Tate ring, and let
![]() $A \hookrightarrow B$
be a finite Galois extension with Galois group G. Equip B with the canonical structure as a Tate ring as in Lemma 4.1. Then the action of G preserves
$A \hookrightarrow B$
be a finite Galois extension with Galois group G. Equip B with the canonical structure as a Tate ring as in Lemma 4.1. Then the action of G preserves
![]() $B^{\circ }$
. Moreover, if further A is preuniform, then
$B^{\circ }$
. Moreover, if further A is preuniform, then
![]() $(B^{\circ })^G=A^{\circ }$
.
$(B^{\circ })^G=A^{\circ }$
.
Proof. Let
![]() $A_0$
be a ring of definition of A, and let
$A_0$
be a ring of definition of A, and let
![]() $t\in A_0$
be a pseudouniformizer of A. As in the proof of [Reference Nakazato and Shimomoto45, Lem. 2.20], we can take a ring of definition
$t\in A_0$
be a pseudouniformizer of A. As in the proof of [Reference Nakazato and Shimomoto45, Lem. 2.20], we can take a ring of definition
![]() $B_0$
of B that is finitely generated as an
$B_0$
of B that is finitely generated as an
![]() $A_0$
-module and satisfies
$A_0$
-module and satisfies
![]() $B=B_0[\frac {1}{t}]$
. Pick
$B=B_0[\frac {1}{t}]$
. Pick
![]() $b\in B^{\circ }$
and
$b\in B^{\circ }$
and
![]() $\sigma \in G$
arbitrarily. Then there is some
$\sigma \in G$
arbitrarily. Then there is some
![]() $l>0$
such that
$l>0$
such that
![]() $t^lb^n\in B_0$
and, therefore,
$t^lb^n\in B_0$
and, therefore,
![]() $t^l\sigma (b)^n\in \sigma (B_0)$
for every
$t^l\sigma (b)^n\in \sigma (B_0)$
for every
![]() $n>0$
. Meanwhile, since
$n>0$
. Meanwhile, since
![]() $\sigma (B_0)$
is also finitely generated as an
$\sigma (B_0)$
is also finitely generated as an
![]() $A_0$
-module, we have
$A_0$
-module, we have
![]() $t^{l'}\sigma (B_0)\subset B_0$
for some
$t^{l'}\sigma (B_0)\subset B_0$
for some
![]() $l'>0$
. Hence
$l'>0$
. Hence
![]() $\sigma (b)$
is also almost integral over
$\sigma (b)$
is also almost integral over
![]() $B_0$
. Thus, the action of G preserves
$B_0$
. Thus, the action of G preserves
![]() $B^{\circ }$
. If further A is preuniform, then we have
$B^{\circ }$
. If further A is preuniform, then we have
by Proposition 4.3(2), as wanted.
4.2 Rational functions associated with regular sequences
We specialize the above results to study the rings of rational functions associated with regular sequences.
Notation. Let A be Tate ring,
![]() $(A_0, (t))$
a pair of definition of A, and
$(A_0, (t))$
a pair of definition of A, and
![]() $f,g \in A_{0}$
regular elements. Then we define a Tate ring
$f,g \in A_{0}$
regular elements. Then we define a Tate ring
![]() $A(\frac {f}{g})$
as the Tate ring associated with
$A(\frac {f}{g})$
as the Tate ring associated with
![]() $(A_{0}[\frac {f}{g}], (t))$
(see Definition 2.8(2)), and also define
$(A_{0}[\frac {f}{g}], (t))$
(see Definition 2.8(2)), and also define
![]() $A\{\frac {f}{g}\}$
as the separated completion of
$A\{\frac {f}{g}\}$
as the separated completion of
![]() $A(\frac {f}{g})$
. These Tate rings are independent of the choice of a pair of definition
$A(\frac {f}{g})$
. These Tate rings are independent of the choice of a pair of definition
![]() $(A_{0}, (t))$
.
$(A_{0}, (t))$
.
One can clarify the relationship between
![]() $A\{\frac {f}{g}\}$
and
$A\{\frac {f}{g}\}$
and
![]() $\widehat {A}\{\frac {f}{g}\}$
.
$\widehat {A}\{\frac {f}{g}\}$
.
Lemma 4.6. Let A be Tate ring, let
![]() $(A_0, (t))$
a pair of definition of A, and let
$(A_0, (t))$
a pair of definition of A, and let
![]() $f,g \in A_{0}$
be regular elements. Let
$f,g \in A_{0}$
be regular elements. Let
![]() $\mathcal {A}$
be the separated completion of
$\mathcal {A}$
be the separated completion of
![]() ${A}$
. Suppose that
${A}$
. Suppose that
![]() $(f,g)$
forms a regular sequence in
$(f,g)$
forms a regular sequence in
![]() $A_{0}$
. Then
$A_{0}$
. Then
![]() $\mathcal {A}\{\frac {f}{g}\}$
is the separated completions of
$\mathcal {A}\{\frac {f}{g}\}$
is the separated completions of
![]() $A(\frac {f}{g})$
.
$A(\frac {f}{g})$
.
Proof. For any
![]() $A_{0}$
-algebra B, we let
$A_{0}$
-algebra B, we let
![]() $\widehat {B}$
denote the t-adic completion of B. By definition,
$\widehat {B}$
denote the t-adic completion of B. By definition,
![]() $A(\frac {f}{g})$
has a pair of definition
$A(\frac {f}{g})$
has a pair of definition
![]() $(A_{0}[\frac {f}{g}], (t))$
. Moreover, the completion
$(A_{0}[\frac {f}{g}], (t))$
. Moreover, the completion
![]() $\widehat {A_{0}[\frac {f}{g}]}$
is canonically isomorphic to
$\widehat {A_{0}[\frac {f}{g}]}$
is canonically isomorphic to
![]() $\widehat {\widehat {A_{0}}[\frac {f}{g}]}$
by Proposition 3.14 because
$\widehat {\widehat {A_{0}}[\frac {f}{g}]}$
by Proposition 3.14 because
![]() $(f,g)$
forms a regular sequence. Since
$(f,g)$
forms a regular sequence. Since
![]() $(\widehat {\widehat {A_{0}}[\frac {f}{g}]}, (t))$
is a pair of definition of
$(\widehat {\widehat {A_{0}}[\frac {f}{g}]}, (t))$
is a pair of definition of
![]() $\mathcal {A}\{\frac {f}{g}\}$
, the assertion follows.
$\mathcal {A}\{\frac {f}{g}\}$
, the assertion follows.
Let us inspect topological features of finite étale algebras over the rings of rational functions.
Proposition 4.7. Let A be a Tate ring, and let
![]() $(A_{0}, (t))$
be a pair of definition of A. Let
$(A_{0}, (t))$
be a pair of definition of A. Let
![]() $g\in A_{0}$
be a regular element. Suppose that
$g\in A_{0}$
be a regular element. Suppose that
![]() $A(\frac {t}{g})$
is preuniform. Let
$A(\frac {t}{g})$
is preuniform. Let
![]() $B'$
be a finite étale
$B'$
be a finite étale
![]() $A[\frac {1}{g}]$
-algebra. Let
$A[\frac {1}{g}]$
-algebra. Let
![]() $B_{0}$
be the integral closure of
$B_{0}$
be the integral closure of
![]() $A_{0}$
in
$A_{0}$
in
![]() $B'$
, and let B be the Tate ring associated with
$B'$
, and let B be the Tate ring associated with
![]() $(B_{0},(t))$
. Let
$(B_{0},(t))$
. Let
![]() $B^{\prime }_{t/g}$
be the finite étale
$B^{\prime }_{t/g}$
be the finite étale
![]() $A(\frac {t}{g})$
-algebra
$A(\frac {t}{g})$
-algebra
![]() $B'$
equipped with the canonical structure as a Tate ring (cf. Lemma 4.1). Then the following assertions hold:
$B'$
equipped with the canonical structure as a Tate ring (cf. Lemma 4.1). Then the following assertions hold:
-
1.
 $B^{\prime }_{t/g}$
is preuniform.
$B^{\prime }_{t/g}$
is preuniform. -
2.
 $B^{\prime }_{t/g}=B(\frac {t}{g})$
as topological rings. In particular,
$B^{\prime }_{t/g}=B(\frac {t}{g})$
as topological rings. In particular,
 $B(\frac {t}{g})$
is preuniform.
$B(\frac {t}{g})$
is preuniform.
Proof. By Proposition 4.3(1),
![]() $B^{\prime }_{t/g}$
is preuniform, and
$B^{\prime }_{t/g}$
is preuniform, and
![]() $\big ((A_{0}[\frac {t}{g}])^+_{B'}, (t)\big )$
is a pair of definition of
$\big ((A_{0}[\frac {t}{g}])^+_{B'}, (t)\big )$
is a pair of definition of
![]() $B^{\prime }_{t/g}$
. Moreover,
$B^{\prime }_{t/g}$
. Moreover,
![]() $\big (B_0[\frac {t}{g}]\big )^+_{B'}=\big (A_{0}[\frac {t}{g}]\big )^+_{B'}$
because
$\big (B_0[\frac {t}{g}]\big )^+_{B'}=\big (A_{0}[\frac {t}{g}]\big )^+_{B'}$
because
![]() $B_{0}=(A_{0})^{+}_{B'}$
. Thus, we find that
$B_{0}=(A_{0})^{+}_{B'}$
. Thus, we find that
![]() $B_{0}[\frac {t}{g}]$
is bounded in
$B_{0}[\frac {t}{g}]$
is bounded in
![]() $B^{\prime }_{t/g}$
. Hence, it suffices to show that
$B^{\prime }_{t/g}$
. Hence, it suffices to show that
![]() $B_{0}[\frac {t}{g}]\subset B^{\prime }_{t/g}$
is open. Note that
$B_{0}[\frac {t}{g}]\subset B^{\prime }_{t/g}$
is open. Note that
![]() $B^{\prime }_{t/g}=(A_{0}[\frac {1}{tg}])^{+}_{B'}=(A_{0})^{+}_{B'}[\frac {1}{tg}]=B_{0}[\frac {1}{tg}]$
as rings. By Lemma 4.1(2), one can take a ring of definition
$B^{\prime }_{t/g}=(A_{0}[\frac {1}{tg}])^{+}_{B'}=(A_{0})^{+}_{B'}[\frac {1}{tg}]=B_{0}[\frac {1}{tg}]$
as rings. By Lemma 4.1(2), one can take a ring of definition
![]() $B^{\prime }_{0}$
of
$B^{\prime }_{0}$
of
![]() $B^{\prime }_{t/g}$
which is module finite over
$B^{\prime }_{t/g}$
which is module finite over
![]() $A_0[\frac {t}{g}]$
. Then, since
$A_0[\frac {t}{g}]$
. Then, since
![]() $A_0[\frac {t}{g}]\subset B_{0}[\frac {t}{g}]$
and
$A_0[\frac {t}{g}]\subset B_{0}[\frac {t}{g}]$
and
![]() $(B_{0}[\frac {t}{g}])[\frac {1}{t}]=B^{\prime }_{t/g}$
as rings, there exists some
$(B_{0}[\frac {t}{g}])[\frac {1}{t}]=B^{\prime }_{t/g}$
as rings, there exists some
![]() $l>0$
such that
$l>0$
such that
![]() $t^{l}B^{\prime }_{0}\subset B_{0}[\frac {t}{g}]$
. Hence
$t^{l}B^{\prime }_{0}\subset B_{0}[\frac {t}{g}]$
. Hence
![]() $B_{0}[\frac {t}{g}]$
is open in
$B_{0}[\frac {t}{g}]$
is open in
![]() $B^{\prime }_{t/g}$
, as desired.
$B^{\prime }_{t/g}$
, as desired.
Proposition 4.8. Keep the notations and assumptions as in Proposition 4.7. Suppose further that
![]() $(t,g)$
forms a regular sequence in
$(t,g)$
forms a regular sequence in
![]() $A_{0}$
and
$A_{0}$
and
![]() $B_{0}$
. Let
$B_{0}$
. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be the separated completions of A and B, respectively. Then the following assertions hold:
$\mathcal {B}$
be the separated completions of A and B, respectively. Then the following assertions hold:
-
1.
 $\mathcal {A}\{\frac {t}{g}\}$
and
$\mathcal {A}\{\frac {t}{g}\}$
and
 $\mathcal {B}\{\frac {t}{g}\}$
are the separated completions of
$\mathcal {B}\{\frac {t}{g}\}$
are the separated completions of
 $A(\frac {t}{g})$
and
$A(\frac {t}{g})$
and
 $B(\frac {t}{g})$
, respectively.
$B(\frac {t}{g})$
, respectively. -
2.
 $\mathcal {A}\{\frac {t}{g}\}$
and
$\mathcal {A}\{\frac {t}{g}\}$
and
 $\mathcal {B}\{\frac {t}{g}\}$
are uniform.
$\mathcal {B}\{\frac {t}{g}\}$
are uniform. -
3. Set
 $\mathcal {B}^{\prime }_{t/g}:=B'\otimes _{A[\frac {1}{g}]}\mathcal {A}\{\frac {t}{g}\}$
, and equip
$\mathcal {B}^{\prime }_{t/g}:=B'\otimes _{A[\frac {1}{g}]}\mathcal {A}\{\frac {t}{g}\}$
, and equip
 $\mathcal {B}^{\prime }_{t/g}$
with the canonical structure as a Tate ring that is module-finite over
$\mathcal {B}^{\prime }_{t/g}$
with the canonical structure as a Tate ring that is module-finite over
 $\mathcal {A} \{\frac {t}{g}\}$
(cf. Lemma 4.1). Then we have isomorphisms of topological rings (4.1)(where
$\mathcal {A} \{\frac {t}{g}\}$
(cf. Lemma 4.1). Then we have isomorphisms of topological rings (4.1)(where $$ \begin{align} \mathcal{B}^{\prime}_{t/g}\cong \widehat{B^{\prime}_{t/g}}\cong \widehat{B(\frac{t}{g})}\cong\mathcal{B}\{\frac{t}{g}\} \end{align} $$
$$ \begin{align} \mathcal{B}^{\prime}_{t/g}\cong \widehat{B^{\prime}_{t/g}}\cong \widehat{B(\frac{t}{g})}\cong\mathcal{B}\{\frac{t}{g}\} \end{align} $$
 $\widehat {B^{\prime }_{t/g}}$
and
$\widehat {B^{\prime }_{t/g}}$
and
 $\widehat {B(\frac {t}{g})}$
denote the separated completions). In particular,
$\widehat {B(\frac {t}{g})}$
denote the separated completions). In particular,
 $\mathcal {B}^{\prime }_{t/g}$
is uniform.
$\mathcal {B}^{\prime }_{t/g}$
is uniform.
Proof. The assertion (1) follows from Lemma 4.6. Thus, since
![]() $A(\frac {t}{g})$
and
$A(\frac {t}{g})$
and
![]() $B(\frac {t}{g})$
are preuniform by Proposition 4.7, the assertion (2) follows from [Reference Nakazato and Shimomoto45, Prop. 2.4 (1)]. Let us prove (3). By the assertion (1) and Proposition 4.3(3),
$B(\frac {t}{g})$
are preuniform by Proposition 4.7, the assertion (2) follows from [Reference Nakazato and Shimomoto45, Prop. 2.4 (1)]. Let us prove (3). By the assertion (1) and Proposition 4.3(3),
![]() $\mathcal {B}^{\prime }_{t/g}$
is uniform. Moreover, by Corollary 4.4, the natural
$\mathcal {B}^{\prime }_{t/g}$
is uniform. Moreover, by Corollary 4.4, the natural
![]() $A[\frac {1}{g}]$
-algebra homomorphism
$A[\frac {1}{g}]$
-algebra homomorphism
is an isomorphism which restricts to an isomorphism of rings
![]() ${\mathcal {B}}^{\prime \circ }_{t/g}\xrightarrow {\cong }\widehat {B^{\prime \circ }_{t/g}}$
. Since
${\mathcal {B}}^{\prime \circ }_{t/g}\xrightarrow {\cong }\widehat {B^{\prime \circ }_{t/g}}$
. Since
![]() ${\mathcal {B}}^{\prime \circ }_{t/g}$
and
${\mathcal {B}}^{\prime \circ }_{t/g}$
and
![]() $B^{\prime \circ }_{t/g}$
are rings of definitions of
$B^{\prime \circ }_{t/g}$
are rings of definitions of
![]() $\mathcal {B}^{\prime }_{t/g}$
and
$\mathcal {B}^{\prime }_{t/g}$
and
![]() $B^{\prime }_{t/g}$
, respectively, (4.2) gives an isomorphism of topological rings
$B^{\prime }_{t/g}$
, respectively, (4.2) gives an isomorphism of topological rings
![]() $\mathcal {B}^{\prime }_{t/g}\xrightarrow {\cong } \widehat {B^{\prime }_{t/g}}$
. The other isomorphism in (4.1) follows from the assertion (1) and Proposition 4.7(2).
$\mathcal {B}^{\prime }_{t/g}\xrightarrow {\cong } \widehat {B^{\prime }_{t/g}}$
. The other isomorphism in (4.1) follows from the assertion (1) and Proposition 4.7(2).
For example, the assumption of regularity in Proposition 4.8 is realized in the following situation.
Lemma 4.9. Keep the notations and assumptions as in Proposition 4.7. Suppose that
![]() $A_{0}$
is a normal ring, and there exists a ring map
$A_{0}$
is a normal ring, and there exists a ring map
![]() $f: R\to A_0$
with the following properties.
$f: R\to A_0$
with the following properties.
-
1. R is a Noetherian N-2 normal domain.Footnote 6
-
2. There exist
 $t_0\in f^{-1}(t)$
and
$t_0\in f^{-1}(t)$
and
 $g_{0}\in f^{-1}(g)$
such that the height of the ideal
$g_{0}\in f^{-1}(g)$
such that the height of the ideal
 $(t_{0},g_{0})\subset R$
is
$(t_{0},g_{0})\subset R$
is
 $2$
.
$2$
. -
3. f is integral.
-
4.
 $f(R\setminus \{0\})$
consists of regular elements of
$f(R\setminus \{0\})$
consists of regular elements of
 $A_{0}$
.
$A_{0}$
.
Then,
![]() $(t, g)$
forms a regular sequence on
$(t, g)$
forms a regular sequence on
![]() $A_{0}$
and
$A_{0}$
and
![]() $B_{0}$
.
$B_{0}$
.
To prove Lemma 4.9, we need a more fundamental lemma.
Lemma 4.10. Let A be a normal ring that is torsion-free and integral over a Noetherian N-2 normal domain R. Assume that
![]() $(x,y)$
is an ideal of R such that the height of
$(x,y)$
is an ideal of R such that the height of
![]() $(x,y)$
is
$(x,y)$
is
![]() $2$
. Then
$2$
. Then
![]() $x,y$
forms a regular sequence on A.
$x,y$
forms a regular sequence on A.
Proof. If A is the zero ring, then any sequence in A forms a regular sequence. Thus, we assume that A is not the zero ring below. Notice that then the map
![]() $R\to A$
is injective because it is torsion-free and R is a domain.
$R\to A$
is injective because it is torsion-free and R is a domain.
Since R is a Noetherian normal domain, every associated prime of the quotient ring
![]() $R/(x)$
is minimal by Serre’s normality criterion (see [Reference Swanson and Huneke59, Th. 4.5.3]). Thus,
$R/(x)$
is minimal by Serre’s normality criterion (see [Reference Swanson and Huneke59, Th. 4.5.3]). Thus,
![]() $\overline {y} \in R/(x)$
is a regular element by the assumption that the height of
$\overline {y} \in R/(x)$
is a regular element by the assumption that the height of
![]() $(x,y)$
is
$(x,y)$
is
![]() $2$
.Footnote
7
That is,
$2$
.Footnote
7
That is,
![]() $x,y$
is a regular sequence on R. Let
$x,y$
is a regular sequence on R. Let
![]() $\operatorname {Frac}(R)$
be the field of fractions of R. Then, since
$\operatorname {Frac}(R)$
be the field of fractions of R. Then, since
![]() $R \to A$
is integral and torsion-free, it follows that
$R \to A$
is integral and torsion-free, it follows that
![]() $\operatorname {Frac}(R) \otimes _R A$
is the total ring of fractions of A. Let
$\operatorname {Frac}(R) \otimes _R A$
is the total ring of fractions of A. Let
![]() $\operatorname {Frac}(R) \to B$
be a finite-dimensional subextension of
$\operatorname {Frac}(R) \to B$
be a finite-dimensional subextension of
![]() $\operatorname {Frac}(R) \otimes _R A$
and denote by
$\operatorname {Frac}(R) \otimes _R A$
and denote by
![]() $R^+_B$
be the integral closure of R in B. Since B is a reduced finite
$R^+_B$
be the integral closure of R in B. Since B is a reduced finite
![]() $\operatorname {Frac}(R)$
-algebra, it is a finite product of fields. Hence,
$\operatorname {Frac}(R)$
-algebra, it is a finite product of fields. Hence,
![]() $R \to R^+_B$
is module-finite and
$R \to R^+_B$
is module-finite and
![]() $R^+_B$
is a Noetherian normal ring because R is N-2. We can write
$R^+_B$
is a Noetherian normal ring because R is N-2. We can write
![]() $R^+_B= \prod _{i=1}^m R_i$
, where
$R^+_B= \prod _{i=1}^m R_i$
, where
![]() $R \to R_i$
is module-finite and
$R \to R_i$
is module-finite and
![]() $R_i$
is a normal domain. In this case, we see that the height of
$R_i$
is a normal domain. In this case, we see that the height of
![]() $(x,y)R_i$
is
$(x,y)R_i$
is
![]() $2$
for each i and thus,
$2$
for each i and thus,
![]() $x, y$
is a regular sequence on
$x, y$
is a regular sequence on
![]() $R^+_B$
. Since A is a normal ring, it can be written as a colimit of such
$R^+_B$
. Since A is a normal ring, it can be written as a colimit of such
![]() $R^+_B$
. So we conclude that
$R^+_B$
. So we conclude that
![]() $x,y$
is regular on A.
$x,y$
is regular on A.
Now, we can deduce Lemma 4.9 easily.
Proof of Lemma 4.9
Since
![]() $A_{0}$
is normal, so is
$A_{0}$
is normal, so is
![]() $A_{0}[\frac {1}{tg}]$
(
$A_{0}[\frac {1}{tg}]$
(
![]() $=A[\frac {1}{g}]$
). Hence, the étale
$=A[\frac {1}{g}]$
). Hence, the étale
![]() $A[\frac {1}{g}]$
-algebra
$A[\frac {1}{g}]$
-algebra
![]() $B'$
is normal, which implies that
$B'$
is normal, which implies that
![]() $B_{0}$
is normal because it is integrally closed in
$B_{0}$
is normal because it is integrally closed in
![]() $B'$
. Since the map
$B'$
. Since the map
![]() $A[\frac {1}{g}]\to B'$
is flat, it sends any regular element of
$A[\frac {1}{g}]\to B'$
is flat, it sends any regular element of
![]() $A_{0}$
to a regular element of
$A_{0}$
to a regular element of
![]() $B_{0}$
. Thus, since
$B_{0}$
. Thus, since
![]() $f(R\setminus \{0\})\subset A_{0}$
consists of regular elements, the composite map
$f(R\setminus \{0\})\subset A_{0}$
consists of regular elements, the composite map
defines the structure as a torsion-free integral R-algebra on
![]() $B_{0}$
. Therefore, we can apply Lemma 4.10 to deduce the assertion.
$B_{0}$
. Therefore, we can apply Lemma 4.10 to deduce the assertion.
5 A variant of perfectoid Abhyankar’s lemma for almost Witt-perfect rings
Let
![]() $p>0$
be a prime number. For the sake of reader’s convenience, we recall the definition of Witt-perfect rings due to Davis and Kedlaya (see [Reference Davis and Kedlaya15], [Reference Davis and Kedlaya16]).
$p>0$
be a prime number. For the sake of reader’s convenience, we recall the definition of Witt-perfect rings due to Davis and Kedlaya (see [Reference Davis and Kedlaya15], [Reference Davis and Kedlaya16]).
Definition 5.1 (Witt-perfect ring)
For a prime number
![]() $p>0$
, we say that a ring A is p-Witt-perfect (simply Witt-perfect), if the Witt-Frobenius map
$p>0$
, we say that a ring A is p-Witt-perfect (simply Witt-perfect), if the Witt-Frobenius map
![]() $ \mathbf {F}:\mathbf {W}_{p^n}(A) \to \mathbf {W}_{p^{n-1}}(A)$
is surjective for all
$ \mathbf {F}:\mathbf {W}_{p^n}(A) \to \mathbf {W}_{p^{n-1}}(A)$
is surjective for all
![]() $n \ge 2$
.
$n \ge 2$
.
The most part of this article will deal with p-torsion-free Witt-perfect rings. Let us recall the almost version of the Witt-perfect condition as introduced in [Reference Nakazato and Shimomoto45].
Definition 5.2 (Almost Witt-perfect ring)
Let A be a p-torsion-free ring with an element
![]() $\varpi \in A$
admitting a compatible system of p-power roots
$\varpi \in A$
admitting a compatible system of p-power roots
![]() $\varpi ^{\frac {1}{p^n}} \in A$
. Then we say that A is
$\varpi ^{\frac {1}{p^n}} \in A$
. Then we say that A is
![]() $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect, if the following conditions are satisfied.
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect, if the following conditions are satisfied.
-
1. The Frobenius endomorphism on
 $A/(p)$
is
$A/(p)$
is
 $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost surjective.
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost surjective. -
2. For every
 $a\in A$
and every
$a\in A$
and every
 $n>0$
, there is an element
$n>0$
, there is an element
 $b \in A$
such that
$b \in A$
such that
 $b^p \equiv p\varpi ^{\frac {1}{p^n}}a\ \pmod {p^2}$
.
$b^p \equiv p\varpi ^{\frac {1}{p^n}}a\ \pmod {p^2}$
.
For applications, we often consider the case that
![]() $\varpi \in A$
is a regular element and A is (completely) integrally closed in
$\varpi \in A$
is a regular element and A is (completely) integrally closed in
![]() $A[\frac {1}{p}]$
.Footnote
8
If one takes
$A[\frac {1}{p}]$
.Footnote
8
If one takes
![]() $\varpi =1$
, then it is shown that
$\varpi =1$
, then it is shown that
![]() $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost Witt perfectness coincides with the Witt-perfectness (see [Reference Nakazato and Shimomoto45] for details). Let us recall the following fact (see [Reference Nakazato and Shimomoto45, Prop. 3.20]).
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost Witt perfectness coincides with the Witt-perfectness (see [Reference Nakazato and Shimomoto45] for details). Let us recall the following fact (see [Reference Nakazato and Shimomoto45, Prop. 3.20]).
Proposition 5.3. Let V be a p-adically separated p-torsion-free valuation ring, and let A be a p-torsion-free
![]() $V[T^{\frac {1}{p^{\infty }}}]$
-algebra. Set
$V[T^{\frac {1}{p^{\infty }}}]$
-algebra. Set
![]() $\varpi ^{\frac {1}{p^n}}:=T^{\frac {1}{p^n}}\cdot 1\in A$
for every
$\varpi ^{\frac {1}{p^n}}:=T^{\frac {1}{p^n}}\cdot 1\in A$
for every
![]() $n\geq 0$
and denote by
$n\geq 0$
and denote by
![]() $\widehat {V}$
and
$\widehat {V}$
and
![]() $\widehat {A}$
the p-adic completions of V and A, respectively. Then the following conditions are equivalent:
$\widehat {A}$
the p-adic completions of V and A, respectively. Then the following conditions are equivalent:
-
(a) V is a Witt-perfect valuation ring of rank
 $1$
and A is
$1$
and A is
 $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect and integrally closed (resp. completely integrally closed) in
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect and integrally closed (resp. completely integrally closed) in
 $A[\frac {1}{p}]$
.
$A[\frac {1}{p}]$
. -
(b) There exist a perfectoid field K and a
 $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost perfectoid
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost perfectoid
 $K\langle T^{\frac {1}{p^{\infty }}}\rangle $
-algebra
$K\langle T^{\frac {1}{p^{\infty }}}\rangle $
-algebra
 $\mathcal {A}$
with the following properties:
$\mathcal {A}$
with the following properties:-
• K is a Banach ring associated with
 $(\widehat {V}, (p))$
, the norm on K is multiplicative and
$(\widehat {V}, (p))$
, the norm on K is multiplicative and
 $K^{\circ }=\widehat {V}$
;
$K^{\circ }=\widehat {V}$
; -
•
 $\mathcal {A}$
is a Banach ring associated with
$\mathcal {A}$
is a Banach ring associated with
 $(\widehat {A},(p))$
and
$(\widehat {A},(p))$
and
 $\widehat {A}$
is open and integrally closed in
$\widehat {A}$
is open and integrally closed in
 $\mathcal {A}$
(resp.
$\mathcal {A}$
(resp.
 $\mathcal {A}^{\circ }=\widehat {A}$
);
$\mathcal {A}^{\circ }=\widehat {A}$
); -
• the bounded ring map of Banach rings
 $K\langle T^{\frac {1}{p^{\infty }}}\rangle \to \mathcal {A}$
is induced by the ring map
$K\langle T^{\frac {1}{p^{\infty }}}\rangle \to \mathcal {A}$
is induced by the ring map
 $V[T^{\frac {1}{p^{\infty }}}]\to A$
.
$V[T^{\frac {1}{p^{\infty }}}]\to A$
.
-
Remark 5.4.
-
1. In Proposition 5.3, one is allowed to map T to
 $pg \in A$
, in which case A is a
$pg \in A$
, in which case A is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring for some
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring for some
 $g \in A$
. We will consider almost Witt-perfect rings of this type.
$g \in A$
. We will consider almost Witt-perfect rings of this type. -
2. The advantage of working with (almost) Witt-perfect rings is in the fact that one need not impose p-adic completeness condition on a ring. Let
 $A:=W(k)[[x_2,\ldots ,x_d]]$
be the power series algebra over the ring of Witt vectors of a perfect field k of characteristic
$A:=W(k)[[x_2,\ldots ,x_d]]$
be the power series algebra over the ring of Witt vectors of a perfect field k of characteristic
 $p>0$
. Then is a Witt-perfect algebra that is an integrally closed domain and integral, faithfully flat over A. The p-adic completion
$p>0$
. Then is a Witt-perfect algebra that is an integrally closed domain and integral, faithfully flat over A. The p-adic completion $$ \begin{align*}A_{\infty}:=\bigcup_{n>0} W(k)[p^{\frac{1}{p^n}}][[x_2^{\frac{1}{p^n}},\ldots,x_d^{\frac{1}{p^n}}]] \end{align*} $$
$$ \begin{align*}A_{\infty}:=\bigcup_{n>0} W(k)[p^{\frac{1}{p^n}}][[x_2^{\frac{1}{p^n}},\ldots,x_d^{\frac{1}{p^n}}]] \end{align*} $$
 $\widehat {A_{\infty }}$
of
$\widehat {A_{\infty }}$
of
 $A_{\infty }$
is integral perfectoid. While
$A_{\infty }$
is integral perfectoid. While
 $A \to \widehat {A_{\infty }}$
remains flat by [Reference Yekutieli63, Th. 1.1], it is not integral. The ring
$A \to \widehat {A_{\infty }}$
remains flat by [Reference Yekutieli63, Th. 1.1], it is not integral. The ring
 $A_{\infty }$
will be used essentially in the construction of almost Cohen–Macaulay algebras later. A similar construction for complete ramified regular local rings appears in [Reference Shimomoto57, Prop. 4.9].
$A_{\infty }$
will be used essentially in the construction of almost Cohen–Macaulay algebras later. A similar construction for complete ramified regular local rings appears in [Reference Shimomoto57, Prop. 4.9].
Another important example of a Witt-perfect ring is given by an arbitrary absolutely integrally closed domain A, where A is a faithfully flat
 $\mathbb {Z}_p$
-algebra. The p-adic completion
$\mathbb {Z}_p$
-algebra. The p-adic completion
 $\widehat {A}$
is an integral perfectoid algebra over
$\widehat {A}$
is an integral perfectoid algebra over
 $\widehat {\mathbb {Z}_p[p^{\frac {1}{p^{\infty }}}]}$
. Indeed, as A is absolutely integrally closed in its field of fractions, it contains
$\widehat {\mathbb {Z}_p[p^{\frac {1}{p^{\infty }}}]}$
. Indeed, as A is absolutely integrally closed in its field of fractions, it contains
 $\mathbb {Z}_p^+$
. Hence
$\mathbb {Z}_p^+$
. Hence
 $\widehat {A}$
is a
$\widehat {A}$
is a
 $\widehat {\mathbb {Z}_p^+}$
-algebra.
$\widehat {\mathbb {Z}_p^+}$
-algebra.
5.1 Variants of Riemann’s extension theorems
In the context of commutative ring theory, Riemann’s extension theorem often means a kind of theorem that gives a satisfactory answer to Problem 1 in §3.2. Such a theorem for perfectoid algebras is a key result to the proof of the Direct Summand Conjecture and its derived variant (see [Reference André2], [Reference Bhatt9]). In this subsection, we establish two types of decompleted variant of the perfectoid Riemann’s extension theorem (see Theorems 5.11 and 5.16).
5.1.1 Zariskian Riemann’s extension theorem
We start with recalling the definition of adically Zariskian rings.
Definition 5.5. Let A be ring with an ideal
![]() $I \subset A$
. Then we say that A is I-adically Zariskian if I is contained in every maximal ideal of A.
$I \subset A$
. Then we say that A is I-adically Zariskian if I is contained in every maximal ideal of A.
Note that Zariskianness is preserved under integral ring maps by [Reference Matsumura40, Sec. 9 and Lem. 2]. In other words, for an I-adically Zariskian ring A, any integral A-algebra B is
![]() $IB$
-adically Zariskian.
$IB$
-adically Zariskian.
We then introduce an important notion using semivaluations (cf. Definition 2.6). In the following definition, for a semivaluation
![]() $|\cdot |$
, we denote by
$|\cdot |$
, we denote by
![]() $V_{|\cdot |}$
the valuation ring described in Definition 2.9.
$V_{|\cdot |}$
the valuation ring described in Definition 2.9.
Definition 5.6. Let
![]() $D \subset C$
be a ring extension, and let us set
$D \subset C$
be a ring extension, and let us set
where
![]() $\sim $
is generated by natural equivalence classes of semivaluations.
$\sim $
is generated by natural equivalence classes of semivaluations.
Let us prove the following algebraic result.
Proposition 5.7. Let
![]() $(C,D)$
be a pair of rings such that C is the localization of D with respect to some multiplicative set consisting of regular elements. Suppose that D is an integral extension of a Noetherian ring R. Fix a (possibly empty) subset
$(C,D)$
be a pair of rings such that C is the localization of D with respect to some multiplicative set consisting of regular elements. Suppose that D is an integral extension of a Noetherian ring R. Fix a (possibly empty) subset
![]() $\mathcal {S} \subset D$
that consists of only regular elements. Then one has
$\mathcal {S} \subset D$
that consists of only regular elements. Then one has
where
![]() $D^+_C$
is the integral closure of D in C. In particular,
$D^+_C$
is the integral closure of D in C. In particular,
![]() $D^+_C$
does not depend on the choice of
$D^+_C$
does not depend on the choice of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Proof. Since the containment
![]() $\subset $
is clear by the definition of
$\subset $
is clear by the definition of
![]() $\operatorname {Val}(C,D)$
, let us prove the reverse containment
$\operatorname {Val}(C,D)$
, let us prove the reverse containment
![]() $\supset $
. Let
$\supset $
. Let
![]() $y \in C$
be such that
$y \in C$
be such that
![]() $|y| \le 1$
, where
$|y| \le 1$
, where
![]() $|\cdot | \in \operatorname {Val}(C,D)$
satisfies
$|\cdot | \in \operatorname {Val}(C,D)$
satisfies
![]() $|g| \ne 0$
for every
$|g| \ne 0$
for every
![]() $g \in \mathcal {S}$
. Let
$g \in \mathcal {S}$
. Let
![]() $D[\frac {1}{y}]$
be the subring of the localization
$D[\frac {1}{y}]$
be the subring of the localization
![]() $C[\frac {1}{y}]$
which is generated by
$C[\frac {1}{y}]$
which is generated by
![]() $y^{-1}=\frac {1}{y}$
over D.Footnote
9
Consider the ring extension
$y^{-1}=\frac {1}{y}$
over D.Footnote
9
Consider the ring extension
![]() $D[\frac {1}{y}] \subset C[\frac {1}{y}]$
. First, suppose that
$D[\frac {1}{y}] \subset C[\frac {1}{y}]$
. First, suppose that
![]() $y^{-1}$
is a unit in
$y^{-1}$
is a unit in
![]() $D[\frac {1}{y}]$
. Then we can write
$D[\frac {1}{y}]$
. Then we can write
for
![]() $a_i \in D$
. Then we have
$a_i \in D$
. Then we have
![]() $y^n-a_{n-1}y^{n-1}-\cdots -a_0=0$
. Hence
$y^n-a_{n-1}y^{n-1}-\cdots -a_0=0$
. Hence
![]() $y \in C$
is integral over D and
$y \in C$
is integral over D and
![]() $y \in D^+_C$
.
$y \in D^+_C$
.
To derive a contradiction, suppose that
![]() $y^{-1} \in D[\frac {1}{y}]$
is not a unit. We may assume that y is not nilpotent. Choose a prime ideal
$y^{-1} \in D[\frac {1}{y}]$
is not a unit. We may assume that y is not nilpotent. Choose a prime ideal
![]() $\frak {m} \subset D[\frac {1}{y}]$
such that
$\frak {m} \subset D[\frac {1}{y}]$
such that
![]() $y^{-1} \in \frak {m}$
. Let
$y^{-1} \in \frak {m}$
. Let
![]() $\frak {p} \subset D[\frac {1}{y}]$
be a minimal prime ideal satisfying
$\frak {p} \subset D[\frac {1}{y}]$
be a minimal prime ideal satisfying
![]() $\frak {p} \subset \frak {m}$
. On the other hand,
$\frak {p} \subset \frak {m}$
. On the other hand,
![]() $R[\frac {1}{y}] \subset D[\frac {1}{y}]$
is an integral extension and
$R[\frac {1}{y}] \subset D[\frac {1}{y}]$
is an integral extension and
![]() $R[\frac {1}{y}]$
is Noetherian by Hilbert’s Basis Theorem.
$R[\frac {1}{y}]$
is Noetherian by Hilbert’s Basis Theorem.
Then, one can find a valuation ring
![]() $D[\frac {1}{y}]/\frak {p} \subset V \subset \operatorname {Frac}(D[\frac {1}{y}]/\frak {p})$
such that the center (the maximal ideal) of V contains
$D[\frac {1}{y}]/\frak {p} \subset V \subset \operatorname {Frac}(D[\frac {1}{y}]/\frak {p})$
such that the center (the maximal ideal) of V contains
![]() $y^{-1}$
and the Krull dimension of V is
$y^{-1}$
and the Krull dimension of V is
![]() $1$
: More concretely, one can construct V in the following way. Let
$1$
: More concretely, one can construct V in the following way. Let
![]() $\frak {n}:=\frak {m} \cap R[\frac {1}{y}]$
and
$\frak {n}:=\frak {m} \cap R[\frac {1}{y}]$
and
![]() $\frak {q}:=\frak {p} \cap R[\frac {1}{y}]$
. Then we have a Noetherian subdomain
$\frak {q}:=\frak {p} \cap R[\frac {1}{y}]$
. Then we have a Noetherian subdomain
![]() $R[\frac {1}{y}]/\frak {q} \subset \operatorname {Frac}(R[\frac {1}{y}]/\frak {q})$
. By [Reference Swanson and Huneke59, Th. 6.3.2 and 6.3.3], there is a Noetherian valuation ring
$R[\frac {1}{y}]/\frak {q} \subset \operatorname {Frac}(R[\frac {1}{y}]/\frak {q})$
. By [Reference Swanson and Huneke59, Th. 6.3.2 and 6.3.3], there is a Noetherian valuation ring
![]() $V_{\frak {n}}$
such that
$V_{\frak {n}}$
such that
![]() $R[\frac {1}{y}]/\frak {q} \subset V_{\frak {n}} \subset \operatorname {Frac}(R[\frac {1}{y}]/\frak {q})$
and the center of
$R[\frac {1}{y}]/\frak {q} \subset V_{\frak {n}} \subset \operatorname {Frac}(R[\frac {1}{y}]/\frak {q})$
and the center of
![]() $V_{\frak {n}}$
contains
$V_{\frak {n}}$
contains
![]() $\overline {\frak {n}} \subset R[\frac {1}{y}]/\frak {q}$
. We have the commutative diagram:
$\overline {\frak {n}} \subset R[\frac {1}{y}]/\frak {q}$
. We have the commutative diagram:

where V is defined as the localization of the integral closure of
![]() $V_{\frak {n}}$
in
$V_{\frak {n}}$
in
![]() $\operatorname {Frac}(D[\frac {1}{y}]/\frak {p})$
(this integral closure is a so-called Prüfer domain) at the maximal ideal containing
$\operatorname {Frac}(D[\frac {1}{y}]/\frak {p})$
(this integral closure is a so-called Prüfer domain) at the maximal ideal containing
![]() $\overline {\frak {m}}$
. So V is a valuation ring of Krull dimension
$\overline {\frak {m}}$
. So V is a valuation ring of Krull dimension
![]() $1$
and we have the composite map
$1$
and we have the composite map
![]() $D \to D[\frac {1}{y}] \to V$
. Let
$D \to D[\frac {1}{y}] \to V$
. Let
![]() $|\cdot |_V$
denote the corresponding valuation. Moreover,
$|\cdot |_V$
denote the corresponding valuation. Moreover,
![]() $\mathcal {S} \subset D$
consists of regular elements and
$\mathcal {S} \subset D$
consists of regular elements and
![]() $C[\frac {1}{y}]$
is the localization of D, so the image of elements in
$C[\frac {1}{y}]$
is the localization of D, so the image of elements in
![]() $\mathcal {S}$
remains regular elements in
$\mathcal {S}$
remains regular elements in
![]() $C[\frac {1}{y}]$
and thus in the subring
$C[\frac {1}{y}]$
and thus in the subring
![]() $D[\frac {1}{y}]$
. As
$D[\frac {1}{y}]$
. As
![]() $\frak {p}$
is a minimal prime ideal of
$\frak {p}$
is a minimal prime ideal of
![]() $D[\frac {1}{y}]$
,
$D[\frac {1}{y}]$
,
![]() $g \notin \frak {p}$
for every
$g \notin \frak {p}$
for every
![]() $g \in \mathcal {S}$
. So we find that
$g \in \mathcal {S}$
. So we find that
![]() $|g| _V\ne 0$
and, in particular, this implies that
$|g| _V\ne 0$
and, in particular, this implies that
![]() $D \to D[\frac {1}{y}] \to V$
extends to the map
$D \to D[\frac {1}{y}] \to V$
extends to the map
![]() $C \to C[\frac {1}{y}] \to \operatorname {Frac}(V)$
and the semivaluation on
$C \to C[\frac {1}{y}] \to \operatorname {Frac}(V)$
and the semivaluation on
![]() $(C,D)$
induced by
$(C,D)$
induced by
![]() $|\cdot |_V$
gives a point
$|\cdot |_V$
gives a point
![]() $|\cdot |_C \in \operatorname {Val}(C,D)$
.
$|\cdot |_C \in \operatorname {Val}(C,D)$
.
By our assumption, we have
![]() $|y|_C \le 1$
. Since
$|y|_C \le 1$
. Since
![]() $y^{-1} \in V$
is in the center, we know
$y^{-1} \in V$
is in the center, we know
![]() $|y^{-1}|_C< 1$
. However, these facts are not compatible with
$|y^{-1}|_C< 1$
. However, these facts are not compatible with
![]() $|y|_C|y^{-1}|_C=|yy^{-1}|_C=1$
and thus,
$|y|_C|y^{-1}|_C=|yy^{-1}|_C=1$
and thus,
![]() $y^{-1} \in D[\frac {1}{y}]$
must be a unit, as desired.
$y^{-1} \in D[\frac {1}{y}]$
must be a unit, as desired.
The above proposition has the following implication: Keep in mind that
![]() $A^+$
stands for an open integrally closed subring in a Tate ring A.
$A^+$
stands for an open integrally closed subring in a Tate ring A.
Corollary 5.8. Let
![]() $(A,A^+)$
be an affinoid Tate ring with a fixed pseudouniformizer
$(A,A^+)$
be an affinoid Tate ring with a fixed pseudouniformizer
![]() $t \in A^+$
such that
$t \in A^+$
such that
![]() $A^+$
is t-adically Zariskian and
$A^+$
is t-adically Zariskian and
![]() $A^+$
is integral over a Noetherian ring. For a regular element
$A^+$
is integral over a Noetherian ring. For a regular element
![]() $g \in A^+$
, let us set
$g \in A^+$
, let us set
![]() $(C,D):=(A[\frac {1}{g}],A^+)$
. Then we have
$(C,D):=(A[\frac {1}{g}],A^+)$
. Then we have
Finally, let
![]() $\operatorname {Val}(C,D)_{|t|<1}$
be the set of all elements
$\operatorname {Val}(C,D)_{|t|<1}$
be the set of all elements
![]() $|\cdot | \in \operatorname {Val}(C,D)$
for which
$|\cdot | \in \operatorname {Val}(C,D)$
for which
![]() $0<|t|<1$
. Then the natural map
$0<|t|<1$
. Then the natural map
![]() $(A,A^+) \to (C,D)$
induces an injection
$(A,A^+) \to (C,D)$
induces an injection
![]() $\operatorname {Val}(C,D)_{|t|<1} \hookrightarrow \operatorname {Spa}(A,A^+)$
.
$\operatorname {Val}(C,D)_{|t|<1} \hookrightarrow \operatorname {Spa}(A,A^+)$
.
Proof. Keep the notation as in the proof of Proposition 5.7. The point is that one can choose the valuation domain V so as to satisfy the required property. So assume that
![]() $y \in A[\frac {1}{g}]$
satisfies
$y \in A[\frac {1}{g}]$
satisfies
![]() $|y| \le 1$
for all
$|y| \le 1$
for all
![]() $|\cdot | \in \operatorname {Val}(A[\frac {1}{g}],A^+)$
and
$|\cdot | \in \operatorname {Val}(A[\frac {1}{g}],A^+)$
and
![]() $y^{-1} \in A^+[\frac {1}{y}]$
is not a unit. Then we can find a maximal ideal
$y^{-1} \in A^+[\frac {1}{y}]$
is not a unit. Then we can find a maximal ideal
![]() $\frak {m} \subset A^+[\frac {1}{y}]$
such that
$\frak {m} \subset A^+[\frac {1}{y}]$
such that
![]() $y^{-1} \in \frak {m}$
, which gives the surjection
$y^{-1} \in \frak {m}$
, which gives the surjection
![]() $A^+ \twoheadrightarrow A^+[\frac {1}{y}]/\frak {m}$
and let
$A^+ \twoheadrightarrow A^+[\frac {1}{y}]/\frak {m}$
and let
![]() $\frak {n} \subset A^+$
be its kernel. Then
$\frak {n} \subset A^+$
be its kernel. Then
![]() $\frak {n}$
is a maximal ideal of
$\frak {n}$
is a maximal ideal of
![]() $A^+$
. The element
$A^+$
. The element
![]() $t \in A^+$
is in the Jacobson radical by assumption, so we have
$t \in A^+$
is in the Jacobson radical by assumption, so we have
![]() $t \in \frak {n}$
. There is a chain of prime ideals
$t \in \frak {n}$
. There is a chain of prime ideals
![]() $\frak {p} \subset \frak {m} \subset A^+[\frac {1}{y}]$
such that
$\frak {p} \subset \frak {m} \subset A^+[\frac {1}{y}]$
such that
![]() $\frak {p}$
is minimal and
$\frak {p}$
is minimal and
![]() $t,y^{-1} \in \frak {m}$
. Then, we have the associated valuation ring
$t,y^{-1} \in \frak {m}$
. Then, we have the associated valuation ring
![]() $(V,|\cdot |_V)$
and the map
$(V,|\cdot |_V)$
and the map
![]() $A^+[\frac {1}{y}]/{\frak p} \hookrightarrow V$
. It follows from the above construction that
$A^+[\frac {1}{y}]/{\frak p} \hookrightarrow V$
. It follows from the above construction that
![]() $|t|_V<1$
, establishing (5.1). As t maps into the maximal ideal of the rank
$|t|_V<1$
, establishing (5.1). As t maps into the maximal ideal of the rank
![]() $1$
valuation ring V, it follows from [Reference Bhatt8, Prop. 7.3.7] that
$1$
valuation ring V, it follows from [Reference Bhatt8, Prop. 7.3.7] that
![]() $|\cdot |_V$
pulled back to
$|\cdot |_V$
pulled back to
![]() $A^+$
gives a point of
$A^+$
gives a point of
![]() $\operatorname {Spa}(A,A^+)$
. Finally, the injectivity of the claimed map is clear from the construction.
$\operatorname {Spa}(A,A^+)$
. Finally, the injectivity of the claimed map is clear from the construction.
Corollary 5.8 can be formulated also in terms of adic geometry as in Corollary 5.9, where the notion of maximal separated quotient plays an essential role. For generalities on topological spaces and maximal separated quotients, we refer the reader to [Reference Fujiwara and Kato19, Chap. 0, 2.3(c)] and [Reference Kedlaya and Liu37, Defn. 2.4.8] (see also [Reference Munster42] for the construction and properties of maximal separated quotients in general topology). A detailed construction of the maximal separated quotient of an adic space via rank
![]() $1$
valuations is found in [Reference Bhatt8, Prop. 7.4.13].
$1$
valuations is found in [Reference Bhatt8, Prop. 7.4.13].
Corollary 5.9. Let
![]() $(A, A^+)$
be an affinoid Tate ring, and let
$(A, A^+)$
be an affinoid Tate ring, and let
![]() $(A_0, (t))$
be a pair of definition of A. Let
$(A_0, (t))$
be a pair of definition of A. Let
![]() $s\in A_0$
be an element such that
$s\in A_0$
be an element such that
![]() $t\in sa:0$
. Let
$t\in sa:0$
. Let
![]() $X=\text {Spa}(A, A^+)$
, and let U be the subspace of X:
$X=\text {Spa}(A, A^+)$
, and let U be the subspace of X:
Suppose that
![]() $A_0$
is s-adically Zariskian and integral over a Noetherian ring. Then we have
$A_0$
is s-adically Zariskian and integral over a Noetherian ring. Then we have
where
![]() $[U]$
denotes the maximal separated quotient of U.
$[U]$
denotes the maximal separated quotient of U.
Proof. Since we have the containments
(the third inclusion holds because
![]() $|\cdot |_x$
is of rank
$|\cdot |_x$
is of rank
![]() $1$
), it suffices to show that
$1$
), it suffices to show that
By assumption, there exists
![]() $g\in A_0$
such that
$g\in A_0$
such that
![]() $t=sg$
. Let B be the Tate ring associated with
$t=sg$
. Let B be the Tate ring associated with
![]() $(A_0,(s))$
and
$(A_0,(s))$
and
![]() $B^+:=(A_0)^+_B$
. Then we have
$B^+:=(A_0)^+_B$
. Then we have
![]() $A=B[\frac {1}{g}]$
,
$A=B[\frac {1}{g}]$
,
![]() $(A_0)^+_A=(B^+)^+_{B[\frac {1}{g}]}$
and
$(A_0)^+_A=(B^+)^+_{B[\frac {1}{g}]}$
and
by Corollary 5.8. Let us deduce (5.2) from (5.3) by constructing a canonical bijection
Any point
![]() $|\cdot |\in \operatorname {Val}(B[\frac {1}{g}],B^+)_{|s|<1}$
satisfies that
$|\cdot |\in \operatorname {Val}(B[\frac {1}{g}],B^+)_{|s|<1}$
satisfies that
![]() $|a|\leq 1$
for any
$|a|\leq 1$
for any
![]() $a\in A_0$
and
$a\in A_0$
and
![]() $|t|=|sg|<1$
. Thus, since
$|t|=|sg|<1$
. Thus, since
![]() $|\cdot |$
is of rank
$|\cdot |$
is of rank
![]() $1$
,
$1$
,
![]() $|\cdot |$
gives a continuous semivaluation on A such that
$|\cdot |$
gives a continuous semivaluation on A such that
![]() $|A^{\circ }|\leq 1$
. Hence, we have a canonical injection
$|A^{\circ }|\leq 1$
. Hence, we have a canonical injection
Moreover,
![]() $B^+\subset A^+$
, and
$B^+\subset A^+$
, and
![]() $|s|_{x}\neq 0$
for every
$|s|_{x}\neq 0$
for every
![]() $x\in [U]$
because
$x\in [U]$
because
![]() $s\in A$
is invertible. Hence (5.4) is also surjective, as desired.
$s\in A$
is invertible. Hence (5.4) is also surjective, as desired.
Indeed, the following immediate corollary is already documented in a treatise on rigid geometry.
Corollary 5.10 (Compare [Reference Fujiwara and Kato19, II, Th. 8.1.11 and 8.2.19])
Let A be a complete and separated Tate ring. Suppose that A has a ring of definition
![]() $A_0$
that is Noetherian. Set
$A_0$
that is Noetherian. Set
![]() $X=\operatorname {Spa}\big (A, (A_0)^+_A\big )$
. Then we have
$X=\operatorname {Spa}\big (A, (A_0)^+_A\big )$
. Then we have
Let us discuss an application of the above results. Let A be a ring with regular elements
![]() $t,g$
. For every
$t,g$
. For every
![]() $j>0$
, we let
$j>0$
, we let
![]() $A^{j}$
denote the Tate ring associated with
$A^{j}$
denote the Tate ring associated with
![]() $(A[\frac {t^{j}}{g}], (t))$
. Then the set of
$(A[\frac {t^{j}}{g}], (t))$
. Then the set of
![]() ${A}$
-algebras
${A}$
-algebras
![]() $\{{A}^j\}_{j>0}$
naturally forms an inverse system, where
$\{{A}^j\}_{j>0}$
naturally forms an inverse system, where
![]() ${A}^{j+1} \to {A}^{j}$
is the isomorphism
${A}^{j+1} \to {A}^{j}$
is the isomorphism
![]() $A[\frac {t^{j+1}}{g}][\frac {1}{t}]\xrightarrow {\cong } A[\frac {t^j}{g}][\frac {1}{t}]$
defined by the rule
$A[\frac {t^{j+1}}{g}][\frac {1}{t}]\xrightarrow {\cong } A[\frac {t^j}{g}][\frac {1}{t}]$
defined by the rule
 $$ \begin{align} \frac{t^{j+1}}{g}\mapsto t\cdot\frac{t^{j}}{g} \end{align} $$
$$ \begin{align} \frac{t^{j+1}}{g}\mapsto t\cdot\frac{t^{j}}{g} \end{align} $$
and compatible with the isomorphisms
![]() $A[\frac {t^j}{g}][\frac {1}{t}]\xrightarrow {\cong }A[\frac {1}{t g}]\ (j>0)$
. Then
$A[\frac {t^j}{g}][\frac {1}{t}]\xrightarrow {\cong }A[\frac {1}{t g}]\ (j>0)$
. Then
![]() ${A}^{j+1} \to {A}^{j}$
is a continuous ring map between Tate rings, so that it induces
${A}^{j+1} \to {A}^{j}$
is a continuous ring map between Tate rings, so that it induces
![]() $A^{j+1\circ } \to A^{j\circ }$
. There is the following commutative diagram:
$A^{j+1\circ } \to A^{j\circ }$
. There is the following commutative diagram:

Now, we can prove the following type of extension theorem, which is fitting into the framework of Zariskian geometry (see [Reference Tanaka60] for more details).
Theorem 5.11 (Zariskian Riemann’s extension theorem)
Let A be a ring with a regular element t that is t-adically Zariskian and integral over a Noetherian ring. Let
![]() $g\in A$
be a regular element. Let
$g\in A$
be a regular element. Let
![]() $A^{j}$
be the Tate ring associated with
$A^{j}$
be the Tate ring associated with
![]() $\big (A[\frac {t^j}{g}], (t)\big )$
for every integer
$\big (A[\frac {t^j}{g}], (t)\big )$
for every integer
![]() $j>0$
. Then we have an isomorphism of rings
$j>0$
. Then we have an isomorphism of rings
 $$ \begin{align*}A^+_{A[\frac{1}{tg}]} \xrightarrow{\cong} \varprojlim_{j>0}A^{j\circ}. \end{align*} $$
$$ \begin{align*}A^+_{A[\frac{1}{tg}]} \xrightarrow{\cong} \varprojlim_{j>0}A^{j\circ}. \end{align*} $$
Proof. By assumption, we have a canonical ring isomorphism
![]() $\varphi _j: A[\frac {1}{tg}]\xrightarrow {\cong }A^{j}$
for each
$\varphi _j: A[\frac {1}{tg}]\xrightarrow {\cong }A^{j}$
for each
![]() $j>0$
. By restricting
$j>0$
. By restricting
![]() $\varphi _j$
to
$\varphi _j$
to
![]() $A^+_{A[\frac {1}{tg}]}$
, we obtain the ring map
$A^+_{A[\frac {1}{tg}]}$
, we obtain the ring map
![]() $\varphi ^+_j: A^+_{A[\frac {1}{tg}]}\to A^{j\circ }$
. Then
$\varphi ^+_j: A^+_{A[\frac {1}{tg}]}\to A^{j\circ }$
. Then
![]() $\{\varphi _j\}_{j>0}$
and
$\{\varphi _j\}_{j>0}$
and
![]() $\{\varphi ^+_j\}_{j>0}$
induce the commutative diagram of ring maps:
$\{\varphi ^+_j\}_{j>0}$
induce the commutative diagram of ring maps:

where
![]() $\varphi $
is an isomorphism and the vertical maps are injective. Thus, it suffices to prove that (5.6) is Cartesian. Pick
$\varphi $
is an isomorphism and the vertical maps are injective. Thus, it suffices to prove that (5.6) is Cartesian. Pick
![]() $c\in A[\frac {1}{tg}]$
such that
$c\in A[\frac {1}{tg}]$
such that
![]() $\varphi _j(c)\in A^{j\circ }$
for every
$\varphi _j(c)\in A^{j\circ }$
for every
![]() $j>0$
. Let us show that c lies in
$j>0$
. Let us show that c lies in
![]() $A^+_{A[\frac {1}{tg}]}$
by applying Corollary 5.9. For this, we consider the
$A^+_{A[\frac {1}{tg}]}$
by applying Corollary 5.9. For this, we consider the
![]() $(tg)$
-adic topology: let
$(tg)$
-adic topology: let
![]() $A_{(tg)}$
be the Tate ring associated with
$A_{(tg)}$
be the Tate ring associated with
![]() $\big (A, (tg)\big )$
(notice that each
$\big (A, (tg)\big )$
(notice that each
![]() $A^j$
is also the Tate ring associated with
$A^j$
is also the Tate ring associated with
![]() $\big (A[\frac {t^j}{g}], (tg)\big )$
). Let
$\big (A[\frac {t^j}{g}], (tg)\big )$
). Let
![]() $X_{(tg)}=\operatorname {Spa}(A_{(tg)}, A^+_{A_{(tg)}})$
,
$X_{(tg)}=\operatorname {Spa}(A_{(tg)}, A^+_{A_{(tg)}})$
,
![]() $X_{j}=\operatorname {Spa}(A^{j}, A^{j\circ })$
for each
$X_{j}=\operatorname {Spa}(A^{j}, A^{j\circ })$
for each
![]() $j>0$
, and let U be the subspace
$j>0$
, and let U be the subspace
of
![]() $X_{(tg)}$
. Then the underlying ring of
$X_{(tg)}$
. Then the underlying ring of
![]() $A_{(tg)}$
is equal to
$A_{(tg)}$
is equal to
![]() $A[\frac {1}{tg}]$
, and we have
$A[\frac {1}{tg}]$
, and we have
by Corollary 5.9. On the other hand, since
by Proposition 7.1, we have
![]() $|\varphi _j(c)|_{x_j}\leq 1$
for all
$|\varphi _j(c)|_{x_j}\leq 1$
for all
![]() $j>0$
and all
$j>0$
and all
![]() $x_j\in [X_{j}]$
. Now, since
$x_j\in [X_{j}]$
. Now, since
![]() $\varphi _j$
gives a continuous map
$\varphi _j$
gives a continuous map
![]() $\big (A_{(tg)},A^+_{A_{(tg)}}\big ) \to (A^j,A^{j\circ })$
, (5.6) induces the continuous map
$\big (A_{(tg)},A^+_{A_{(tg)}}\big ) \to (A^j,A^{j\circ })$
, (5.6) induces the continuous map
![]() $\varinjlim _{j>0}[X_j]\to [X_{(tg)}]$
, which factors through
$\varinjlim _{j>0}[X_j]\to [X_{(tg)}]$
, which factors through
![]() $[U]$
because
$[U]$
because
![]() $t\in A^{j}$
is topologically nilpotent. Thus, we are reduced to showing that the resulting map
$t\in A^{j}$
is topologically nilpotent. Thus, we are reduced to showing that the resulting map
![]() $f: \varinjlim _{j>0}[X_{j}]\to [U]$
is surjective.
$f: \varinjlim _{j>0}[X_{j}]\to [U]$
is surjective.
Pick
![]() $x\in [U]$
and let
$x\in [U]$
and let
![]() $|\cdot |_x: {A}_{(tg)}\to \mathbb {R}_{\geq 0}$
be a corresponding semivaluation. Let us find some
$|\cdot |_x: {A}_{(tg)}\to \mathbb {R}_{\geq 0}$
be a corresponding semivaluation. Let us find some
![]() $j_0>0$
such that the composite
$j_0>0$
such that the composite
gives a point
![]() $x_{j_0}\in [X_{j_0}]$
for which
$x_{j_0}\in [X_{j_0}]$
for which
![]() $f([x_{j_0}])=x$
. Since
$f([x_{j_0}])=x$
. Since
![]() $|t|_x<1$
and
$|t|_x<1$
and
![]() $|\cdot |_x$
is of rank
$|\cdot |_x$
is of rank
![]() $1$
, there exists some
$1$
, there exists some
![]() $j_0>0$
such that
$j_0>0$
such that
![]() $|\frac {t^{j_0}}{g}|_x<1$
. Then we have
$|\frac {t^{j_0}}{g}|_x<1$
. Then we have
![]() $|A[\frac {t^{j_0}}{g}]|_x\leq 1$
because
$|A[\frac {t^{j_0}}{g}]|_x\leq 1$
because
![]() $|A|_x\leq 1$
and
$|A|_x\leq 1$
and
![]() $|\cdot |_x$
is of rank
$|\cdot |_x$
is of rank
![]() $1$
. Thus, since any
$1$
. Thus, since any
![]() $a\in A^{j_0\circ }$
is almost integral over
$a\in A^{j_0\circ }$
is almost integral over
![]() $A[\frac {t^{j_0}}{g}]$
and
$A[\frac {t^{j_0}}{g}]$
and
![]() $|\cdot |_x$
is of rank 1, we have
$|\cdot |_x$
is of rank 1, we have
![]() $|A^{j_0\circ }|_{x, j_0}\leq 1$
. Hence
$|A^{j_0\circ }|_{x, j_0}\leq 1$
. Hence
![]() $|\cdot |_{x, j_0}$
gives the desired point
$|\cdot |_{x, j_0}$
gives the desired point
![]() $x_{j_0}\in [X_{j_0}]$
.
$x_{j_0}\in [X_{j_0}]$
.
5.1.2 Witt-perfect Riemann’s extension theorem
Next, we shall investigate the Riemann’s extension problem in the context of Witt-perfect rings by transporting the situation to the case of perfectoid algebras, in which case, Riemann’s extension theorem has been studied by André, Bhatt, and Scholze and known to experts. Let us start setting up some notation.
Notation. Fix a prime number
![]() $p>0$
and a p-torsion-free ring A that admits a compatible system of p-power roots
$p>0$
and a p-torsion-free ring A that admits a compatible system of p-power roots
![]() $g^{\frac {1}{p^n}} \in A$
for a regular element
$g^{\frac {1}{p^n}} \in A$
for a regular element
![]() $g \in A$
for
$g \in A$
for
![]() $n>0$
. Moreover, assume the following premises:
$n>0$
. Moreover, assume the following premises:
-
1. A is an algebra over a p-adically separated p-torsion-free Witt-perfect valuation domain V of rank
 $1$
such that
$1$
such that
 $p^{\frac {1}{p^n}} \in V$
for
$p^{\frac {1}{p^n}} \in V$
for
 $n>0$
.
$n>0$
. -
2. A is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring and A is completely integrally closed in
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring and A is completely integrally closed in
 $A[\frac {1}{p}]$
.
$A[\frac {1}{p}]$
. -
3.
 $(p,g)$
is a
$(p,g)$
is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A (while retaining that
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A (while retaining that
 $p,g$
are regular elements).
$p,g$
are regular elements).
In this situation, we use the following notation.
Definition 5.12. Let B be a
![]() $pg$
-torsion-free A-algebra, and let
$pg$
-torsion-free A-algebra, and let
![]() $\widehat {(~)}$
denote the p-adic completion.
$\widehat {(~)}$
denote the p-adic completion.
-
1. We define
 $K:=\widehat {V}[\frac {1}{p}]$
and equip it with the norm
$K:=\widehat {V}[\frac {1}{p}]$
and equip it with the norm
 $||\cdot ||_{\widehat {V}, (p), p}$
in the sense of [Reference Nakazato and Shimomoto45, Defn. 2.26].
$||\cdot ||_{\widehat {V}, (p), p}$
in the sense of [Reference Nakazato and Shimomoto45, Defn. 2.26]. -
2. We define
 $\mathcal {B}:=\widehat {B}[\frac {1}{p}]$
and equip it with the norm
$\mathcal {B}:=\widehat {B}[\frac {1}{p}]$
and equip it with the norm
 $||\cdot ||_{\widehat {B}, (p), p}$
in the sense of [Reference Nakazato and Shimomoto45, Defn. 2.26].
$||\cdot ||_{\widehat {B}, (p), p}$
in the sense of [Reference Nakazato and Shimomoto45, Defn. 2.26]. -
3. For every
 $j>0$
, we define
$j>0$
, we define
 $B^{j}$
as the Tate ring associated with
$B^{j}$
as the Tate ring associated with
 $(B[\frac {p^{j}}{g}], (p))$
(cf. Definition 2.8(2)).
$(B[\frac {p^{j}}{g}], (p))$
(cf. Definition 2.8(2)). -
4. Let
 $\mathcal {C}$
be a Banach
$\mathcal {C}$
be a Banach
 $\mathcal {A}$
-algebra, and let
$\mathcal {A}$
-algebra, and let
 $||\cdot ||_{\mathcal {C}}$
be the norm on it. Put
$||\cdot ||_{\mathcal {C}}$
be the norm on it. Put  $$ \begin{align*}\mathcal{C}_{0}:=\{c\in \mathcal{C}\ |\ ||c||_{\mathcal{C}}\leq 1\}. \end{align*} $$
$$ \begin{align*}\mathcal{C}_{0}:=\{c\in \mathcal{C}\ |\ ||c||_{\mathcal{C}}\leq 1\}. \end{align*} $$
For every
 $j>0$
, we define
$j>0$
, we define
 $\mathcal {C}^{j}=\widehat {\mathcal {C}_{0}[\frac {p^{j}}{g}]}[\frac {1}{p}]$
and equip it with the norm
$\mathcal {C}^{j}=\widehat {\mathcal {C}_{0}[\frac {p^{j}}{g}]}[\frac {1}{p}]$
and equip it with the norm
 $||\cdot ||_{\widehat {\mathcal {C}_{0}[\frac {p^{j}}{g}]}, (p), p}$
in the sense of [Reference Nakazato and Shimomoto45, Defn. 2.26]. In particular,
$||\cdot ||_{\widehat {\mathcal {C}_{0}[\frac {p^{j}}{g}]}, (p), p}$
in the sense of [Reference Nakazato and Shimomoto45, Defn. 2.26]. In particular,
 $\mathcal {B}^{j}$
is the Banach ring
$\mathcal {B}^{j}$
is the Banach ring
 $\widehat {\widehat {B}[\frac {p^{j}}{g}]}[\frac {1}{p}]$
equipped with the norm
$\widehat {\widehat {B}[\frac {p^{j}}{g}]}[\frac {1}{p}]$
equipped with the norm
 $||\cdot ||_{\widehat {\widehat {B}[\frac {p^{j}}{g}]}, (p), p}$
.
$||\cdot ||_{\widehat {\widehat {B}[\frac {p^{j}}{g}]}, (p), p}$
.
Here, we should list several remarks.
Remark 5.13. The notations are as above.
-
1. By Proposition 5.3 (and its proof), K is a perfectoid field and
 $\mathcal {A}$
is a
$\mathcal {A}$
is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost perfectoid algebra over K.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost perfectoid algebra over K. -
2. It follows from Lemma 3.11 that
 $g \in \mathcal {A}$
is a
$g \in \mathcal {A}$
is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost regular element.
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular element. -
3. The natural map
 $\mathcal {A}^{\natural \circ } \hookrightarrow \mathcal {A}^{\circ }$
is a
$\mathcal {A}^{\natural \circ } \hookrightarrow \mathcal {A}^{\circ }$
is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism, where
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism, where
 $\mathcal {A}^{\natural }$
denotes the untilt of the tilt of
$\mathcal {A}^{\natural }$
denotes the untilt of the tilt of
 $\mathcal {A}$
and
$\mathcal {A}$
and
 $\mathcal {A}^{\natural }$
is a perfectoid K-algebra in view of [Reference André1, Prop. 3.5.4].
$\mathcal {A}^{\natural }$
is a perfectoid K-algebra in view of [Reference André1, Prop. 3.5.4]. -
4.
 $\mathcal {B}$
is a Banach
$\mathcal {B}$
is a Banach
 $\mathcal {A}$
-algebra. Moreover,
$\mathcal {A}$
-algebra. Moreover,
 ${\mathcal {B}}^{j}$
is a Banach
${\mathcal {B}}^{j}$
is a Banach
 $\mathcal {B}$
-algebra that is viewed as a ring of analytic functions on the rational subset
$\mathcal {B}$
-algebra that is viewed as a ring of analytic functions on the rational subset
 $\big \{x \in X~\big |~|p^j| \le |g(x)|\big \}$
of
$\big \{x \in X~\big |~|p^j| \le |g(x)|\big \}$
of
 $X:=\operatorname {Spa}(\mathcal {B},\mathcal {B}^{\circ })$
(cf. [Reference Huber32, Prop. 1.3 and 1.6]).
$X:=\operatorname {Spa}(\mathcal {B},\mathcal {B}^{\circ })$
(cf. [Reference Huber32, Prop. 1.3 and 1.6]). -
5. Equip the polynomial ring
 $\mathcal {B}[T]$
with the Gauss norm (cf. [Reference Kedlaya36, Defn. 1.6]), and consider the completion
$\mathcal {B}[T]$
with the Gauss norm (cf. [Reference Kedlaya36, Defn. 1.6]), and consider the completion
 $\mathcal {B}\langle T\rangle $
of it. Let
$\mathcal {B}\langle T\rangle $
of it. Let
 $(gT-p^{j})^{-}$
denote the closure of the ideal
$(gT-p^{j})^{-}$
denote the closure of the ideal
 $(gT-p^{j})$
in
$(gT-p^{j})$
in
 ${\mathcal {B}}\langle T\rangle $
. Then
${\mathcal {B}}\langle T\rangle $
. Then
 ${\mathcal {B}}^{j}$
can be identified with
${\mathcal {B}}^{j}$
can be identified with
 $\mathcal {B}\langle T\rangle /(gT-p^{j})^{-}$
as a ring, and the norm on
$\mathcal {B}\langle T\rangle /(gT-p^{j})^{-}$
as a ring, and the norm on
 ${\mathcal {B}}^{j}$
is equivalent to the quotient norm on
${\mathcal {B}}^{j}$
is equivalent to the quotient norm on
 $\mathcal {B}\langle T\rangle /(gT-p^{j})^{-}$
.
$\mathcal {B}\langle T\rangle /(gT-p^{j})^{-}$
.
The most important case is when
![]() $B=A$
. Let us investigate several properties of
$B=A$
. Let us investigate several properties of
![]() $A^{j}$
and
$A^{j}$
and
![]() $\mathcal {A}^{j}$
. First, we describe the relationship of them.
$\mathcal {A}^{j}$
. First, we describe the relationship of them.
Lemma 5.14. In the situation of Definition 5.12, the following assertions hold for every
![]() $j>0$
.
$j>0$
.
-
1. The natural A-algebra map:
(5.7)(where the completions are p-adic) is a $$ \begin{align} \widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \rightarrow \widehat{\widehat{A}\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \end{align} $$
$$ \begin{align} \widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \rightarrow \widehat{\widehat{A}\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \end{align} $$
 $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
-
2. Let
 $\widehat {A^{j}}$
be the separated completion of
$\widehat {A^{j}}$
be the separated completion of
 $A^{j}$
. Applying the functor
$A^{j}$
. Applying the functor
 $(~)\otimes _{A}A[\frac {1}{p}]$
to (5.7) yields an isomorphism of topological rings:
$(~)\otimes _{A}A[\frac {1}{p}]$
to (5.7) yields an isomorphism of topological rings:  $$ \begin{align*}\widehat{A^{j}}\xrightarrow{\cong} \mathcal{A}^{j}. \end{align*} $$
$$ \begin{align*}\widehat{A^{j}}\xrightarrow{\cong} \mathcal{A}^{j}. \end{align*} $$
-
3. Let
 $\psi _{j}$
denote the composite map
$\psi _{j}$
denote the composite map
 $A[\frac {1}{pg}]=A^{j}\to \widehat {A^{j}}\xrightarrow {\cong } \mathcal {A}^{j}$
. Then we have the following identification of rings: (5.8)
$A[\frac {1}{pg}]=A^{j}\to \widehat {A^{j}}\xrightarrow {\cong } \mathcal {A}^{j}$
. Then we have the following identification of rings: (5.8) $$ \begin{align} A^{j\circ}=A[\frac{1}{pg}] \times_{\mathcal{A}^j} \mathcal{A}^{j\circ}=\Big\{a \in A[\frac{1}{pg}]~\Big|~\psi_{j}(a) \in \mathcal{A}^{j\circ}\Big\}. \end{align} $$
$$ \begin{align} A^{j\circ}=A[\frac{1}{pg}] \times_{\mathcal{A}^j} \mathcal{A}^{j\circ}=\Big\{a \in A[\frac{1}{pg}]~\Big|~\psi_{j}(a) \in \mathcal{A}^{j\circ}\Big\}. \end{align} $$
Proof. (1): By assumption,
![]() $(p,g)$
is a
$(p,g)$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A. Hence, by Proposition 3.14, the natural map
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A. Hence, by Proposition 3.14, the natural map
![]() $\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^n}}\big ]} \to \widehat {\widehat {A}\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^n}}\big ]}$
is a
$\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^n}}\big ]} \to \widehat {\widehat {A}\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^n}}\big ]}$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism for every
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism for every
![]() $n\geq 0$
. Moreover, we have the following commutative diagram:
$n\geq 0$
. Moreover, we have the following commutative diagram:

The vertical maps become isomorphisms after applying
![]() $(~)\otimes _{A}A/p^{m}A$
. Hence, they become isomorphisms after p-adic completion. Hence, by Lemma 2.3, the lower map (5.7) is also a
$(~)\otimes _{A}A/p^{m}A$
. Hence, they become isomorphisms after p-adic completion. Hence, by Lemma 2.3, the lower map (5.7) is also a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
(2): Since
![]() $pgA[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset A[\frac {p^{j}}{g}]$
and
$pgA[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset A[\frac {p^{j}}{g}]$
and
![]() $p^{j+1}=\frac {p^{j}}{g}\cdot pg$
, we have
$p^{j+1}=\frac {p^{j}}{g}\cdot pg$
, we have
![]() $p^{j+1}A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset A[\frac {p^{j}}{g}]$
. Similarly,
$p^{j+1}A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset A[\frac {p^{j}}{g}]$
. Similarly,
![]() $p^{j+1}\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset \widehat {A}[\frac {p^{j}}{g}]$
. Hence, by [Reference Nakazato and Shimomoto45, Lem. 2.5], the ring maps
$p^{j+1}\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset \widehat {A}[\frac {p^{j}}{g}]$
. Hence, by [Reference Nakazato and Shimomoto45, Lem. 2.5], the ring maps
![]() $\widehat {A[\frac {p^{j}}{g}]}\to \widehat {A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
and
$\widehat {A[\frac {p^{j}}{g}]}\to \widehat {A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
and
![]() $\widehat {\widehat {A}[\frac {p^{j}}{g}]}\to \widehat {\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
are injective, and their cokernels are annihilated by
$\widehat {\widehat {A}[\frac {p^{j}}{g}]}\to \widehat {\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
are injective, and their cokernels are annihilated by
![]() $p^{j+1}$
. In particular, they become isomorphisms after inverting p. Hence, one can regard
$p^{j+1}$
. In particular, they become isomorphisms after inverting p. Hence, one can regard
![]() $\widehat {A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
and
$\widehat {A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
and
![]() $\widehat {\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
as rings of definition of
$\widehat {\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
as rings of definition of
![]() $\widehat {A^{j}}$
and
$\widehat {A^{j}}$
and
![]() $\mathcal {A}^{j}$
, respectively.
$\mathcal {A}^{j}$
, respectively.
Since (5.7) is
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost bijective, it becomes an isomorphism after inverting p. Thus, applying the functor
$(p)^{\frac {1}{p^{\infty }}}$
-almost bijective, it becomes an isomorphism after inverting p. Thus, applying the functor
![]() $(~)\otimes _{A}A[\frac {1}{p}]$
to (5.7) yields a canonical isomorphism of rings
$(~)\otimes _{A}A[\frac {1}{p}]$
to (5.7) yields a canonical isomorphism of rings
which restricts to (5.7). Moreover, (5.7) is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost surjective embedding from a ring of definition of
$(p)^{\frac {1}{p^{\infty }}}$
-almost surjective embedding from a ring of definition of
![]() $\widehat {A^{j}}$
into that of
$\widehat {A^{j}}$
into that of
![]() $\mathcal {A}^{j}$
. In particular,
$\mathcal {A}^{j}$
. In particular,
![]() $p(\widehat {\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]})$
is contained in the image of
$p(\widehat {\widehat {A}[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]})$
is contained in the image of
![]() $\widehat {A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
via (5.9). Therefore, (5.9) is also a homeomorphism, as desired.
$\widehat {A[(\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]}$
via (5.9). Therefore, (5.9) is also a homeomorphism, as desired.
(3): Since
![]() $A^{j}=A[\frac {1}{pg}]$
as rings, this assertion immediately follows from the assertion (2) and Corollary 3.2.
$A^{j}=A[\frac {1}{pg}]$
as rings, this assertion immediately follows from the assertion (2) and Corollary 3.2.
Next, we discuss preuniformity (resp. uniformity) of
![]() $A^{j}$
(resp.
$A^{j}$
(resp.
![]() $\mathcal {A}^{j}$
).
$\mathcal {A}^{j}$
).
Proposition 5.15. In the situation of Definition 5.12, the following assertions hold for every
![]() $j>0$
.
$j>0$
.
-
1.
 $\mathcal {A}^{j}$
is a perfectoid K-algebra. In particular,
$\mathcal {A}^{j}$
is a perfectoid K-algebra. In particular,
 $\mathcal {A}^{j}$
is uniform.
$\mathcal {A}^{j}$
is uniform. -
2. There is an
 $A[\frac {p^j}{g}]$
-algebra homomorphism: (5.10)that is
$A[\frac {p^j}{g}]$
-algebra homomorphism: (5.10)that is $$ \begin{align} \widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \xrightarrow{\approx}\mathcal{A}^{j \circ} \end{align} $$
$$ \begin{align} \widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \xrightarrow{\approx}\mathcal{A}^{j \circ} \end{align} $$
 $(p)^{\frac {1}{p^{\infty }}}$
-almost bijective.
$(p)^{\frac {1}{p^{\infty }}}$
-almost bijective.
-
3. The inclusion map:
(5.11)is a $$ \begin{align} A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big] \hookrightarrow A^{j \circ} \end{align} $$
$$ \begin{align} A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big] \hookrightarrow A^{j \circ} \end{align} $$
 $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. In particular,
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. In particular,
 $A^j$
is preuniform.
$A^j$
is preuniform.
-
4. There is an
 $A[\frac {p^j}{g}]$
-algebra isomorphism: Moreover,
$A[\frac {p^j}{g}]$
-algebra isomorphism: Moreover, $$ \begin{align*}\widehat{A^{j\circ}} \xrightarrow{\cong} \mathcal{A}^{j\circ}. \end{align*} $$
$$ \begin{align*}\widehat{A^{j\circ}} \xrightarrow{\cong} \mathcal{A}^{j\circ}. \end{align*} $$
 $A^{j\circ }$
is Witt-perfect.
$A^{j\circ }$
is Witt-perfect.
Proof. (1): Let
![]() $\mathcal {A}^{\natural }$
denote the untilt of the tilt of
$\mathcal {A}^{\natural }$
denote the untilt of the tilt of
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $\mathcal {A}^{\natural }$
is a perfectoid K-algebra in view of [Reference André1, Prop. 3.5.4]. Since the natural map
$\mathcal {A}^{\natural }$
is a perfectoid K-algebra in view of [Reference André1, Prop. 3.5.4]. Since the natural map
![]() $\mathcal {A}^{\natural \circ } \hookrightarrow \mathcal {A}^{\circ }$
is a
$\mathcal {A}^{\natural \circ } \hookrightarrow \mathcal {A}^{\circ }$
is a
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism, the induced map
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism, the induced map
![]() $\mathcal {A}^{\natural \circ }[\frac {p^{j}}{g}] \hookrightarrow \mathcal {A}^{\circ }[\frac {p^{j}}{g}]$
is a
$\mathcal {A}^{\natural \circ }[\frac {p^{j}}{g}] \hookrightarrow \mathcal {A}^{\circ }[\frac {p^{j}}{g}]$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Therefore, the induced map
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Therefore, the induced map
![]() $\widehat {\mathcal {A}^{\natural \circ }[\frac {p^{j}}{g}]} \rightarrow \widehat {\mathcal {A}^{\circ }[\frac {p^{j}}{g}]}$
is also a
$\widehat {\mathcal {A}^{\natural \circ }[\frac {p^{j}}{g}]} \rightarrow \widehat {\mathcal {A}^{\circ }[\frac {p^{j}}{g}]}$
is also a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism by Lemma 2.3. Hence, inverting p yields an isomorphism of topological rings
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism by Lemma 2.3. Hence, inverting p yields an isomorphism of topological rings
![]() $(\mathcal {A}^{\natural })^{j}\to \mathcal {A}^{j}$
. On the other hand,
$(\mathcal {A}^{\natural })^{j}\to \mathcal {A}^{j}$
. On the other hand,
![]() $(\mathcal {A}^{\natural })^j$
is a perfectoid K-algebra by [Reference Scholze52, Th. 6.3 (ii)]. Thus,
$(\mathcal {A}^{\natural })^j$
is a perfectoid K-algebra by [Reference Scholze52, Th. 6.3 (ii)]. Thus,
![]() $\mathcal {A}^j$
is a perfectoid K-algebra.
$\mathcal {A}^j$
is a perfectoid K-algebra.
(2): By the above,
![]() $(\mathcal {A}^{\natural })^{j}\to \mathcal {A}^{j}$
restricts to an isomorphism of rings
$(\mathcal {A}^{\natural })^{j}\to \mathcal {A}^{j}$
restricts to an isomorphism of rings
![]() $(\mathcal {A}^{\natural })^{j\circ }\xrightarrow {\cong }\mathcal {A}^{j\circ }$
. Moreover,
$(\mathcal {A}^{\natural })^{j\circ }\xrightarrow {\cong }\mathcal {A}^{j\circ }$
. Moreover,
![]() $\mathcal {A}^{\natural \circ } \hookrightarrow \mathcal {A}^{\circ }$
induces the
$\mathcal {A}^{\natural \circ } \hookrightarrow \mathcal {A}^{\circ }$
induces the
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism
![]() $\widehat {\mathcal {A}^{\natural \circ }\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]}\xrightarrow {\approx }\widehat {\mathcal {A}^{\circ }\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]}$
by Lemma 2.3, and
$\widehat {\mathcal {A}^{\natural \circ }\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]}\xrightarrow {\approx }\widehat {\mathcal {A}^{\circ }\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]}$
by Lemma 2.3, and
![]() $\mathcal {A}^{\circ }=\widehat {A}$
. Thus, we have the following commutative diagram:
$\mathcal {A}^{\circ }=\widehat {A}$
. Thus, we have the following commutative diagram:

where the left vertical map is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism in view of Scholze’s result [Reference Scholze52, Lem. 6.4]. Hence, the right vertical map:
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism in view of Scholze’s result [Reference Scholze52, Lem. 6.4]. Hence, the right vertical map:
 $$ \begin{align} \widehat{\widehat{A}\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \xrightarrow{\approx} \mathcal{A}^{j \circ} \end{align} $$
$$ \begin{align} \widehat{\widehat{A}\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \xrightarrow{\approx} \mathcal{A}^{j \circ} \end{align} $$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. By considering the composition of (5.7) and (5.12), we obtain the desired
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. By considering the composition of (5.7) and (5.12), we obtain the desired
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism
 $$ \begin{align} \widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \xrightarrow{\approx} \mathcal{A}^{j \circ}. \end{align} $$
$$ \begin{align} \widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]} \xrightarrow{\approx} \mathcal{A}^{j \circ}. \end{align} $$
(3): First recall that
![]() $A^j=A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ][\frac {1}{p}]$
as rings (see the proof of Lemma 5.14(2)). By Lemma 3.1, we have
$A^j=A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ][\frac {1}{p}]$
as rings (see the proof of Lemma 5.14(2)). By Lemma 3.1, we have
 $A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]=A^j \times _{\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ] }[\frac {1}{p}]}\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ] }$
. Moreover, the
$A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]=A^j \times _{\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ] }[\frac {1}{p}]}\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ] }$
. Moreover, the
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism (5.13) extends to an isomorphism of rings
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism (5.13) extends to an isomorphism of rings
![]() $\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]}[\frac {1}{p}] \xrightarrow {\cong } \mathcal {A}^{j}$
. Hence, we have
$\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]}[\frac {1}{p}] \xrightarrow {\cong } \mathcal {A}^{j}$
. Hence, we have
![]() $A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]=A[\frac {1}{pg}] \times _{\mathcal {A}^j}\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ] }$
. On the other hand, by Lemma 5.14(3),
$A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]=A[\frac {1}{pg}] \times _{\mathcal {A}^j}\widehat {A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ] }$
. On the other hand, by Lemma 5.14(3),
![]() $A^{j\circ }=A[\frac {1}{pg}] \times _{\mathcal {A}^j}\mathcal {A}^{j \circ }$
. By construction, the diagram of rings:
$A^{j\circ }=A[\frac {1}{pg}] \times _{\mathcal {A}^j}\mathcal {A}^{j \circ }$
. By construction, the diagram of rings:

is commutative. Thus, the ring map
 $$ \begin{align} A[\frac{1}{pg}] \times_{\mathcal{A}^j}\widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big] }\to A[\frac{1}{pg}] \times_{\mathcal{A}^j}\mathcal{A}^{j \circ} \end{align} $$
$$ \begin{align} A[\frac{1}{pg}] \times_{\mathcal{A}^j}\widehat{A\big[\big(\frac{p^j}{g}\big)^{\frac{1}{p^{\infty}}}\big] }\to A[\frac{1}{pg}] \times_{\mathcal{A}^j}\mathcal{A}^{j \circ} \end{align} $$
induced by (5.13) is isomorphic to
![]() $A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]\hookrightarrow A^{j\circ }$
. Moreover, by Lemma 2.2, (5.14) is a
$A\big [\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}\big ]\hookrightarrow A^{j\circ }$
. Moreover, by Lemma 2.2, (5.14) is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Hence, the first assertion follows. In particular, we have
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Hence, the first assertion follows. In particular, we have
![]() $p^{j+2}A^{j\circ }\subset p^{j+1}A[\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset A[\frac {p^{j}}{g}]$
. Therefore,
$p^{j+2}A^{j\circ }\subset p^{j+1}A[\big (\frac {p^j}{g}\big )^{\frac {1}{p^{\infty }}}]\subset A[\frac {p^{j}}{g}]$
. Therefore,
![]() $A^{j}$
is preuniform.
$A^{j}$
is preuniform.
(4): Since
![]() $A^{j}$
is preuniform, one can apply [Reference Nakazato and Shimomoto45, Prop. 2.4 (1)-(b)] to the inclusion map
$A^{j}$
is preuniform, one can apply [Reference Nakazato and Shimomoto45, Prop. 2.4 (1)-(b)] to the inclusion map
![]() $A[\frac {p^{j}}{g}]\hookrightarrow A^{j\circ }$
and deduce that the induced map
$A[\frac {p^{j}}{g}]\hookrightarrow A^{j\circ }$
and deduce that the induced map
![]() $\widehat {A[\frac {p^{j}}{g}]}\rightarrow \widehat {A^{j\circ }}$
extends to an isomorphism of rings
$\widehat {A[\frac {p^{j}}{g}]}\rightarrow \widehat {A^{j\circ }}$
extends to an isomorphism of rings
On the other hand, Lemma 5.14(2) allows us to extend (5.7) to a ring isomorphism:
By composing the inverse map of (5.15) and (5.16), we obtain the desired isomorphism. In particular,
![]() $A^{j\circ }/(p)\cong \mathcal {A}^{j\circ }/(p)$
and
$A^{j\circ }/(p)\cong \mathcal {A}^{j\circ }/(p)$
and
![]() $A^{j\circ }/(p^{2})\cong \mathcal {A}^{j\circ }/(p^{2})$
. Since
$A^{j\circ }/(p^{2})\cong \mathcal {A}^{j\circ }/(p^{2})$
. Since
![]() $\mathcal {A}^{j}$
is perfectoid,
$\mathcal {A}^{j}$
is perfectoid,
![]() $\mathcal {A}^{j\circ }$
is Witt-perfect by Proposition 5.3. Hence
$\mathcal {A}^{j\circ }$
is Witt-perfect by Proposition 5.3. Hence
![]() $A^{j\circ }$
is also Witt-perfect.
$A^{j\circ }$
is also Witt-perfect.
The set of
![]() $\mathcal {A}$
-algebras
$\mathcal {A}$
-algebras
![]() $\{\mathcal {A}^j\}_{j>0}$
forms an inverse system, where
$\{\mathcal {A}^j\}_{j>0}$
forms an inverse system, where
![]() $\mathcal {A}^{j+1} \to \mathcal {A}^{j}$
is the natural inclusion defined by
$\mathcal {A}^{j+1} \to \mathcal {A}^{j}$
is the natural inclusion defined by
 $$ \begin{align} \frac{p^{j+1}}{g}\mapsto p\cdot\frac{p^{j}}{g}. \end{align} $$
$$ \begin{align} \frac{p^{j+1}}{g}\mapsto p\cdot\frac{p^{j}}{g}. \end{align} $$
Then
![]() $\mathcal {A}^{j+1} \to \mathcal {A}^{j}$
is a continuous map between Banach K-algebras, so that it induces
$\mathcal {A}^{j+1} \to \mathcal {A}^{j}$
is a continuous map between Banach K-algebras, so that it induces
![]() $\mathcal {A}^{j+1\circ } \to \mathcal {A}^{j\circ }$
. Recall that we already defined an inverse system
$\mathcal {A}^{j+1\circ } \to \mathcal {A}^{j\circ }$
. Recall that we already defined an inverse system
![]() $\{A^{j}\}_{j> 0}$
in a similar way (see (5.5)). After the preparations we have made above, we will establish Witt-perfect Riemann’s Extension Theorem (see Theorem 5.16). Notice that it is independent of Zariskian Riemann’s extension theorem (Theorem 5.11).
$\{A^{j}\}_{j> 0}$
in a similar way (see (5.5)). After the preparations we have made above, we will establish Witt-perfect Riemann’s Extension Theorem (see Theorem 5.16). Notice that it is independent of Zariskian Riemann’s extension theorem (Theorem 5.11).
Theorem 5.16 (Witt-perfect Riemann’s extension theorem)
Let A be a p-torsion-free algebra over a p-adically separated p-torsion-free Witt-perfect valuation domain V of rank
![]() $1$
admitting a compatible system of p-power roots
$1$
admitting a compatible system of p-power roots
![]() $p^{\frac {1}{p^n}} \in V$
, together with a regular element
$p^{\frac {1}{p^n}} \in V$
, together with a regular element
![]() $g \in A$
admitting a compatible system of p-power roots
$g \in A$
admitting a compatible system of p-power roots
![]() $g^{\frac {1}{p^n}} \in A$
. Denote by
$g^{\frac {1}{p^n}} \in A$
. Denote by
![]() $\widehat {(~)}$
the p-adic completion and suppose that the following conditions hold:
$\widehat {(~)}$
the p-adic completion and suppose that the following conditions hold:
-
1. A is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring and A is completely integrally closed in
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring and A is completely integrally closed in
 $A[\frac {1}{p}]$
.
$A[\frac {1}{p}]$
. -
2.
 $(p,g)$
is a
$(p,g)$
is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A (which merely says that g is a
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on A (which merely says that g is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost regular element on
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular element on
 $A/(p)$
).
$A/(p)$
).Then the following assertions hold:
-
(a) We have the following identification of rings:
(5.18) $$ \begin{align} \varprojlim_{j>0}A^{j\circ}=A[\frac{1}{pg}]\times_{\mathcal{A}[\frac{1}{g}]}g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}. \end{align} $$
$$ \begin{align} \varprojlim_{j>0}A^{j\circ}=A[\frac{1}{pg}]\times_{\mathcal{A}[\frac{1}{g}]}g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}. \end{align} $$
-
(b) There is an injective A-algebra map:
whose cokernel is $$ \begin{align*}\widehat{\varprojlim_{j>0} A^{j\circ}} \hookrightarrow \varprojlim_{j>0} \widehat{A^{j\circ}}, \end{align*} $$
$$ \begin{align*}\widehat{\varprojlim_{j>0} A^{j\circ}} \hookrightarrow \varprojlim_{j>0} \widehat{A^{j\circ}}, \end{align*} $$
 $(g)^{\frac {1}{p^{\infty }}}$
-almost zero.
$(g)^{\frac {1}{p^{\infty }}}$
-almost zero.
-
Proof. (a): By Lemma 5.14(3), we have canonical isomorphisms:
 $$ \begin{align*} \varprojlim_{j>0} A^{j\circ} \cong\varprojlim_{j>0}\Big(A[\frac{1}{pg}] \times_{\mathcal{A}^j} \mathcal{A}^{j\circ}\Big) \cong A[\frac{1}{pg}] \times_{\varprojlim_{j>0}\mathcal{A}^j} \varprojlim_{j>0}\mathcal{A}^{j\circ}. \end{align*} $$
$$ \begin{align*} \varprojlim_{j>0} A^{j\circ} \cong\varprojlim_{j>0}\Big(A[\frac{1}{pg}] \times_{\mathcal{A}^j} \mathcal{A}^{j\circ}\Big) \cong A[\frac{1}{pg}] \times_{\varprojlim_{j>0}\mathcal{A}^j} \varprojlim_{j>0}\mathcal{A}^{j\circ}. \end{align*} $$
On the other hand, it follows from Riemann’s extension theorem for (almost) perfectoid K-algebras [Reference André1, théorème 4.2.2] (see Theorem 8.1 for the detailed proof) that there is an
![]() $\mathcal {A}^{\circ }$
-algebra isomorphism:
$\mathcal {A}^{\circ }$
-algebra isomorphism:
 $$ \begin{align} g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ} \xrightarrow{\cong} \varprojlim_{j>0} \mathcal{A}^{j\circ}. \end{align} $$
$$ \begin{align} g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ} \xrightarrow{\cong} \varprojlim_{j>0} \mathcal{A}^{j\circ}. \end{align} $$
Moreover, we have the commutative diagram of rings:

where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are the unique maps induced by the universal property of localization. Since the composite map
$\beta $
are the unique maps induced by the universal property of localization. Since the composite map
![]() $g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }\xrightarrow {\cong } \varprojlim _{j>0}\mathcal {A}^{j\circ }\hookrightarrow \varprojlim _{j>0}\mathcal {A}^{j}$
is injective,
$g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }\xrightarrow {\cong } \varprojlim _{j>0}\mathcal {A}^{j\circ }\hookrightarrow \varprojlim _{j>0}\mathcal {A}^{j}$
is injective,
![]() $\beta $
is also injective. Thus, we have
$\beta $
is also injective. Thus, we have
 $$ \begin{align*}A[\frac{1}{pg}] \times_{\varprojlim_{j>0}\mathcal{A}^j} \varprojlim_{j>0}\mathcal{A}^{j\circ} \cong A[\frac{1}{pg}] \times_{\varprojlim_{j>0}\mathcal{A}^j} g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\cong A[\frac{1}{pg}] \times_{(g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ})[\frac{1}{pg}]} g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}. \end{align*} $$
$$ \begin{align*}A[\frac{1}{pg}] \times_{\varprojlim_{j>0}\mathcal{A}^j} \varprojlim_{j>0}\mathcal{A}^{j\circ} \cong A[\frac{1}{pg}] \times_{\varprojlim_{j>0}\mathcal{A}^j} g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\cong A[\frac{1}{pg}] \times_{(g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ})[\frac{1}{pg}]} g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}. \end{align*} $$
Since
![]() $(g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ })[\frac {1}{pg}]=\mathcal {A}[\frac {1}{g}]$
, the assertion follows.
$(g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ })[\frac {1}{pg}]=\mathcal {A}[\frac {1}{g}]$
, the assertion follows.
(b): Since the natural maps
![]() $A\to A^{j\circ } \ (j> 0)$
are compatible with the inverse system
$A\to A^{j\circ } \ (j> 0)$
are compatible with the inverse system
![]() $\{A^{j\circ }\}_{j> 0}$
, one can define a canonical structures as an A-algebra on each one of the rings
$\{A^{j\circ }\}_{j> 0}$
, one can define a canonical structures as an A-algebra on each one of the rings
 $$ \begin{align} \widehat{\varprojlim_{j> 0}A^{j\circ}}=\varprojlim_{n>0}\Big(\big(\varprojlim_{j>0} A^{j\circ}\big)/(p^n)\Big)\ \ \text{and}\ \ \varprojlim_{j>0} \widehat{A^{j\circ}}=\varprojlim_{j>0}\varprojlim_{n>0}\big(A^{j\circ}/(p^n)\big). \end{align} $$
$$ \begin{align} \widehat{\varprojlim_{j> 0}A^{j\circ}}=\varprojlim_{n>0}\Big(\big(\varprojlim_{j>0} A^{j\circ}\big)/(p^n)\Big)\ \ \text{and}\ \ \varprojlim_{j>0} \widehat{A^{j\circ}}=\varprojlim_{j>0}\varprojlim_{n>0}\big(A^{j\circ}/(p^n)\big). \end{align} $$
For a fixed
![]() $n>0$
, consider the exact sequence of inverse systems of A-algebras:
$n>0$
, consider the exact sequence of inverse systems of A-algebras:
![]() $0 \to \{A^{j\circ }\}_{j>0} \xrightarrow {p^n} \{A^{j\circ }\}_{j>0} \to \{A^{j\circ }/(p^n)\}_{j>0} \to 0$
. Then this induces an injective ring map
$0 \to \{A^{j\circ }\}_{j>0} \xrightarrow {p^n} \{A^{j\circ }\}_{j>0} \to \{A^{j\circ }/(p^n)\}_{j>0} \to 0$
. Then this induces an injective ring map
In view of (5.20), taking the inverse limit with respect to
![]() $n>0$
yields the composite ring map
$n>0$
yields the composite ring map
 $$ \begin{align} \widehat{\varprojlim_{j>0} A^{j\circ}} \hookrightarrow \varprojlim_{n>0}\varprojlim_{j>0}\big(A^{j\circ}/(p^n)\big) \xrightarrow{\cong} \varprojlim_{j>0} \widehat{A^{j\circ}}, \end{align} $$
$$ \begin{align} \widehat{\varprojlim_{j>0} A^{j\circ}} \hookrightarrow \varprojlim_{n>0}\varprojlim_{j>0}\big(A^{j\circ}/(p^n)\big) \xrightarrow{\cong} \varprojlim_{j>0} \widehat{A^{j\circ}}, \end{align} $$
which gives an injective A-algebra map. Now, we want to prove that (5.22) is
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost surjective. Note that the map
$(g)^{\frac {1}{p^{\infty }}}$
-almost surjective. Note that the map
![]() $A\to \widehat {\varprojlim _{j>0} A^{j\circ }}$
extends to
$A\to \widehat {\varprojlim _{j>0} A^{j\circ }}$
extends to
![]() $\widehat {A}\to \widehat {\varprojlim _{j>0} A^{j\circ }}$
by the universality of completion (see [Reference Fujiwara and Kato19, Prop. 7.1.9]). Hence, (5.22) yields the composite map of A-algebras
$\widehat {A}\to \widehat {\varprojlim _{j>0} A^{j\circ }}$
by the universality of completion (see [Reference Fujiwara and Kato19, Prop. 7.1.9]). Hence, (5.22) yields the composite map of A-algebras
 $$ \begin{align} \widehat{A} \to \widehat{\varprojlim_{j>0} A^{j\circ}} \xrightarrow{(5.22)} \varprojlim_{j>0} \widehat{A^{j\circ}}. \end{align} $$
$$ \begin{align} \widehat{A} \to \widehat{\varprojlim_{j>0} A^{j\circ}} \xrightarrow{(5.22)} \varprojlim_{j>0} \widehat{A^{j\circ}}. \end{align} $$
On the other hand, by the universality of completion again, we have the commutative squares:

(
![]() $j> 0$
) of which the bottom arrows are compatible with the inverse system
$j> 0$
) of which the bottom arrows are compatible with the inverse system
![]() $\{\widehat {A^{j\circ }}\}_{j> 0}$
. Hence, we obtain an A-algebra map
$\{\widehat {A^{j\circ }}\}_{j> 0}$
. Hence, we obtain an A-algebra map
 $$ \begin{align} \widehat{A}\to \varprojlim_{j\geq 0}\widehat{A^{j\circ}}, \end{align} $$
$$ \begin{align} \widehat{A}\to \varprojlim_{j\geq 0}\widehat{A^{j\circ}}, \end{align} $$
which extends to the isomorphism (5.19) as described in the proof of Theorem 8.1. In particular, (5.24) is
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost surjective. Here, since
$(g)^{\frac {1}{p^{\infty }}}$
-almost surjective. Here, since
![]() $\varprojlim _{j>0} \widehat {A^{j\circ }}$
is p-adically separated, an extension of the map
$\varprojlim _{j>0} \widehat {A^{j\circ }}$
is p-adically separated, an extension of the map
![]() $A\to \varprojlim _{j>0} \widehat {A^{j\circ }}$
along the completion
$A\to \varprojlim _{j>0} \widehat {A^{j\circ }}$
along the completion
![]() $A\to \widehat {A}$
is unique. Therefore, (5.23) is identified with (5.24). Thus, we conclude that (5.23) and hence (5.22) are
$A\to \widehat {A}$
is unique. Therefore, (5.23) is identified with (5.24). Thus, we conclude that (5.23) and hence (5.22) are
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost surjective. This completes the proof of the assertion.
$(g)^{\frac {1}{p^{\infty }}}$
-almost surjective. This completes the proof of the assertion.
By combining Theorem 5.16 with Theorem 5.11, we obtain the following corollary.
Corollary 5.17. Keep the notations and the hypotheses as in Theorem 5.16. Suppose further that A is p-adically Zariskian and integral over a Noetherian ring. Then we have the equality:
 $$ \begin{align} A_{A[\frac{1}{pg}]}^+=\Big\{x \in A[\frac{1}{pg}]~\Big|~\widetilde{\psi}(x) \in g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\Big\}, \end{align} $$
$$ \begin{align} A_{A[\frac{1}{pg}]}^+=\Big\{x \in A[\frac{1}{pg}]~\Big|~\widetilde{\psi}(x) \in g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\Big\}, \end{align} $$
where
![]() $\widetilde {\psi }: A[\frac {1}{pg}]\to \mathcal {A}[\frac {1}{g}]$
is the natural map.
$\widetilde {\psi }: A[\frac {1}{pg}]\to \mathcal {A}[\frac {1}{g}]$
is the natural map.
Proof. By Theorems 5.11 and 5.16(a), we have the commutative diagram of rings:

where
![]() $\pi _{1}$
is the projection map. Since
$\pi _{1}$
is the projection map. Since
![]() $\pi _{1}$
is injective and
$\pi _{1}$
is injective and
![]() $\operatorname {Im} (\pi _{1})=\{x \in A[\frac {1}{pg}]~\Big |~\widetilde {\psi }(x) \in g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }\}$
, the assertion follows.
$\operatorname {Im} (\pi _{1})=\{x \in A[\frac {1}{pg}]~\Big |~\widetilde {\psi }(x) \in g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }\}$
, the assertion follows.
Discussion 5.18. Here is an alternative way to deduce Corollary 5.17. Since
![]() $\mathcal {A}^{j\circ }$
is completely integrally closed in
$\mathcal {A}^{j\circ }$
is completely integrally closed in
![]() $\mathcal {A}^{j\circ }[\frac {1}{pg}]$
, it follows that the right-hand side of (5.19) is completely integrally closed after inverting
$\mathcal {A}^{j\circ }[\frac {1}{pg}]$
, it follows that the right-hand side of (5.19) is completely integrally closed after inverting
![]() $pg$
by Lemma 3.6. This implies that
$pg$
by Lemma 3.6. This implies that
![]() $g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }$
is completely integrally closed after inverting
$g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }$
is completely integrally closed after inverting
![]() $pg$
. Thus,
$pg$
. Thus,
![]() $A_{A[\frac {1}{pg}]}^+$
is contained in the right-hand side of (5.25), and it remains to prove the other inclusion. Note that
$A_{A[\frac {1}{pg}]}^+$
is contained in the right-hand side of (5.25), and it remains to prove the other inclusion. Note that
![]() $A \to g^{-\frac {1}{p^{\infty }}}A$
is almost integral and
$A \to g^{-\frac {1}{p^{\infty }}}A$
is almost integral and
![]() $A \subset g^{-\frac {1}{p^{\infty }}}A \subset A_{A[\frac {1}{pg}]}^+$
by Proposition 7.1. So Corollary 5.8 gives us
$A \subset g^{-\frac {1}{p^{\infty }}}A \subset A_{A[\frac {1}{pg}]}^+$
by Proposition 7.1. So Corollary 5.8 gives us
by setting
![]() $(C,D):=(g^{-\frac {1}{p^{\infty }}}A[\frac {1}{pg}],g^{-\frac {1}{p^{\infty }}}A)$
, where
$(C,D):=(g^{-\frac {1}{p^{\infty }}}A[\frac {1}{pg}],g^{-\frac {1}{p^{\infty }}}A)$
, where
![]() $(g^{-\frac {1}{p^{\infty }}}A)[\frac {1}{p}]$
is equipped with the canonical structure as a Tate ring by declaring that
$(g^{-\frac {1}{p^{\infty }}}A)[\frac {1}{p}]$
is equipped with the canonical structure as a Tate ring by declaring that
![]() $g^{-\frac {1}{p^{\infty }}}A$
is a ring of definition and the topology is p-adic. A result of Huber [Reference Huber31, Prop. 3.9] asserts thatFootnote
10
$g^{-\frac {1}{p^{\infty }}}A$
is a ring of definition and the topology is p-adic. A result of Huber [Reference Huber31, Prop. 3.9] asserts thatFootnote
10
 $$ \begin{align*} \operatorname{Val}(C,D)_{|p|<1} \hookrightarrow \operatorname{Spa} \Big((g^{-\frac{1}{p^{\infty}}}A)[\frac{1}{p}],g^{-\frac{1}{p^{\infty}}}A\Big) \\ \cong \operatorname{Spa} \Big((g^{-\frac{1}{p^{\infty}}}\widehat{A})[\frac{1}{p}],g^{-\frac{1}{p^{\infty}}}\widehat{A}\Big) \cong \operatorname{Spa} \Big((g^{-\frac{1}{p^{\infty}}}\mathcal{A^{\circ}})[\frac{1}{p}],g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\Big), \end{align*} $$
$$ \begin{align*} \operatorname{Val}(C,D)_{|p|<1} \hookrightarrow \operatorname{Spa} \Big((g^{-\frac{1}{p^{\infty}}}A)[\frac{1}{p}],g^{-\frac{1}{p^{\infty}}}A\Big) \\ \cong \operatorname{Spa} \Big((g^{-\frac{1}{p^{\infty}}}\widehat{A})[\frac{1}{p}],g^{-\frac{1}{p^{\infty}}}\widehat{A}\Big) \cong \operatorname{Spa} \Big((g^{-\frac{1}{p^{\infty}}}\mathcal{A^{\circ}})[\frac{1}{p}],g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\Big), \end{align*} $$
which shows that any
![]() $|\cdot | \in \operatorname {Val}(C,D)_{|p|<1}$
extends to an element
$|\cdot | \in \operatorname {Val}(C,D)_{|p|<1}$
extends to an element
![]() $|\cdot | \in \operatorname {Spa}\Big ((g^{-\frac {1}{p^{\infty }}}\mathcal {A^{\circ }})[\frac {1}{p}], g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }\Big )$
for which we know
$|\cdot | \in \operatorname {Spa}\Big ((g^{-\frac {1}{p^{\infty }}}\mathcal {A^{\circ }})[\frac {1}{p}], g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }\Big )$
for which we know
![]() $|x| \le 1$
for
$|x| \le 1$
for
![]() $x \in g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }$
. This fact combined with (5.26) yields the following:
$x \in g^{-\frac {1}{p^{\infty }}}\mathcal {A}^{\circ }$
. This fact combined with (5.26) yields the following:
 $$ \begin{align*}A_{A[\frac{1}{pg}]}^+ \subset \Big\{x \in A[\frac{1}{pg}]~\Big|~\widetilde{\psi}(x) \in g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\Big\} \subset \Big\{x \in C~\Big|~|x| \le 1;~\forall~|\cdot| \in \operatorname{Val}(C,D)_{|p|<1}\Big\}=A_{A[\frac{1}{pg}]}^+, \end{align*} $$
$$ \begin{align*}A_{A[\frac{1}{pg}]}^+ \subset \Big\{x \in A[\frac{1}{pg}]~\Big|~\widetilde{\psi}(x) \in g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ}\Big\} \subset \Big\{x \in C~\Big|~|x| \le 1;~\forall~|\cdot| \in \operatorname{Val}(C,D)_{|p|<1}\Big\}=A_{A[\frac{1}{pg}]}^+, \end{align*} $$
so that (5.25) has been proved.
Remark 5.19.
-
1. Witt-perfect rings are almost never Noetherian and thus, it is natural to ask whether such algebras could be integral over a Noetherian ring. One way for constructing such an algebra over a Noetherian normal domain R is to take the maximal étale extension of R. The details are found in [Reference Shimomoto58] and [Reference Shimomoto56]. We will apply this method to construct almost Cohen–Macaulay algebras in §6.
-
2. As we have seen so far, almost Witt-perfect rings play a central role. So the next question naturally arises in view of the Scholze’s crucial result that the structure presheaf of a perfectoid space is indeed a sheaf. Let
 $(A,A^+)$
be an affinoid Tate ring such that
$(A,A^+)$
be an affinoid Tate ring such that
 $A^+$
is almost Witt-perfect and completely integrally closed in A. Then is the pair
$A^+$
is almost Witt-perfect and completely integrally closed in A. Then is the pair
 $(A,A^+)$
sheafy, or is it stably uniform? Some relevant results are found in the articles [Reference Buzzard and Verberkmoes12] and [Reference Mihara41].
$(A,A^+)$
sheafy, or is it stably uniform? Some relevant results are found in the articles [Reference Buzzard and Verberkmoes12] and [Reference Mihara41].
5.2 Witt-perfect Abhyankar’s lemma
Now, we are prepared to prove the main result, which is a variant of André’s Perfectoid Abhyankar’s Lemma. Here is the statement of the above main theorem.
Theorem 5.20 (Witt-perfect Abhyankar’s lemma)
Let A be a p-torsion-free algebra over a p-adically separated p-torsion-free Witt-perfect valuation domain V of rank
![]() $1$
admitting a compatible system of p-power roots
$1$
admitting a compatible system of p-power roots
![]() $p^{\frac {1}{p^n}} \in V$
, together with a regular element
$p^{\frac {1}{p^n}} \in V$
, together with a regular element
![]() $g \in A$
admitting a compatible system of p-power roots
$g \in A$
admitting a compatible system of p-power roots
![]() $g^{\frac {1}{p^n}} \in A$
. Suppose that the following conditions hold:
$g^{\frac {1}{p^n}} \in A$
. Suppose that the following conditions hold:
-
1. A is a p-adically Zariskian and normal ring.
-
2. A is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring. -
3. A is torsion-free and integral over a Noetherian normal domain R such that
 $g \in R$
and the height of the ideal
$g \in R$
and the height of the ideal
 $(p,g) \subset R$
is
$(p,g) \subset R$
is
 $2$
.
$2$
.Let
 $A[\frac {1}{pg}] \hookrightarrow B'$
be a finite étale extension. Denote by
$A[\frac {1}{pg}] \hookrightarrow B'$
be a finite étale extension. Denote by
 $B:=(g^{-\frac {1}{p^{\infty }}}A)_{B}^{\prime +}$
the integral closure of
$B:=(g^{-\frac {1}{p^{\infty }}}A)_{B}^{\prime +}$
the integral closure of
 $g^{-\frac {1}{p^{\infty }}}A$
in
$g^{-\frac {1}{p^{\infty }}}A$
in
 $B'$
. Then the following statements hold:
$B'$
. Then the following statements hold:-
(a) The Frobenius endomorphism
 $Frob:B/(p) \to B/(p)$
is
$Frob:B/(p) \to B/(p)$
is
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective and it induces an injection
$(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective and it induces an injection
 $B/(p^{\frac {1}{p}}) \hookrightarrow B/(p)$
.
$B/(p^{\frac {1}{p}}) \hookrightarrow B/(p)$
. -
(b) The induced map
 $A/(p^m) \to B/(p^m)$
is
$A/(p^m) \to B/(p^m)$
is
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale for all
$(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale for all
 $m>0$
.
$m>0$
.
-
We first prove the following preliminary result, which substantially contains the assertion (a) of the theorem.
Proposition 5.21. Keep the notation and the assumption as in Theorem 5.20. Then the following assertions hold:
-
1. B is the integral closure of A in
 $B'$
.
$B'$
. -
2. For every
 $j>0$
, the following assertions hold (see Definition 5.12 for the notation).
$j>0$
, the following assertions hold (see Definition 5.12 for the notation).-
(a) Equip
 $B'$
with the canonical structure as a Tate ring that is module-finite over
$B'$
with the canonical structure as a Tate ring that is module-finite over
 $A^{j}$
(as in Lemma 4.1). Then
$A^{j}$
(as in Lemma 4.1). Then
 $B'=B^{j}$
as topological rings. In particular, the ring extension
$B'=B^{j}$
as topological rings. In particular, the ring extension
 $A[\frac {1}{pg}]\hookrightarrow B'$
is identified with a continuous ring map (5.27)
$A[\frac {1}{pg}]\hookrightarrow B'$
is identified with a continuous ring map (5.27) $$ \begin{align} A^{j}\to B^{j}. \end{align} $$
$$ \begin{align} A^{j}\to B^{j}. \end{align} $$
-
(b) Equip
 $B'\otimes _{A[\frac {1}{pg}]}\mathcal {A}^j$
with the canonical structure as a Tate ring that is module-finite over
$B'\otimes _{A[\frac {1}{pg}]}\mathcal {A}^j$
with the canonical structure as a Tate ring that is module-finite over
 $\mathcal {A}^j$
. Then
$\mathcal {A}^j$
. Then
 $B'\otimes _{A[\frac {1}{pg}]}\mathcal {A}^{j}\cong \mathcal {B}^{j}$
as topological rings.
$B'\otimes _{A[\frac {1}{pg}]}\mathcal {A}^{j}\cong \mathcal {B}^{j}$
as topological rings. -
(c)
 $\mathcal {B}^j$
is a perfectoid K-algebra.
$\mathcal {B}^j$
is a perfectoid K-algebra. -
(d) The restriction
 $A^{j\circ } \to B^{j\circ }$
of (5.27) is integral. Moreover, it is
$A^{j\circ } \to B^{j\circ }$
of (5.27) is integral. Moreover, it is
 $(p)^{\frac {1}{p^{\infty }}}$
-almost finite étale, and
$(p)^{\frac {1}{p^{\infty }}}$
-almost finite étale, and
 $B^{j\circ }$
is a Witt-perfect V-algebra.
$B^{j\circ }$
is a Witt-perfect V-algebra.
-
-
3. The natural ring map
 $B\to \varprojlim _{j>0}B^{j\circ }$
(cf. (5.5)) is an isomorphism.
$B\to \varprojlim _{j>0}B^{j\circ }$
(cf. (5.5)) is an isomorphism. -
4. The following assertions hold. In particular, B satisfies the assumptions in Theorem 5.11 (with
 $t=p$
), Proposition 5.15, and Theorem 5.16.
$t=p$
), Proposition 5.15, and Theorem 5.16.-
(a) B is p-adically Zariskian and integral over a Noetherian ring.
-
(b)
 $(p,g)$
is a regular sequence on B.
$(p,g)$
is a regular sequence on B. -
(c) B is completely integrally closed in
 $B[\frac {1}{pg}]$
.
$B[\frac {1}{pg}]$
. -
(d) B is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect ring.
-
-
5. The p-adic completion
 $\widehat {\varprojlim _{j>0}B^{j\circ }}$
is integral
$\widehat {\varprojlim _{j>0}B^{j\circ }}$
is integral
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost perfectoid.Footnote
11
$(pg)^{\frac {1}{p^{\infty }}}$
-almost perfectoid.Footnote
11
Proof of Proposition 5.21
(1): Since A is normal and integral over a Noetherian ring, it is completely integrally closed in
![]() $A[\frac {1}{g}]$
in view of Proposition 7.1. Hence
$A[\frac {1}{g}]$
in view of Proposition 7.1. Hence
![]() $A=g^{-\frac {1}{p^{\infty }}}A$
by Corollary 3.5. Thus the assertion follows.
$A=g^{-\frac {1}{p^{\infty }}}A$
by Corollary 3.5. Thus the assertion follows.
(2): By Proposition 5.15,
![]() $A^{j}$
is preuniform. Hence the assertion (a) follows from Proposition 4.7. In view of Proposition 4.8, to deduce the assertion (b), it suffices to show that
$A^{j}$
is preuniform. Hence the assertion (a) follows from Proposition 4.7. In view of Proposition 4.8, to deduce the assertion (b), it suffices to show that
![]() $(p^j, g)$
forms a regular sequence on A and B. Since A is p-torsion-free and p-adically Zariskian, any prime number in A is a regular element. Thus, if the generic characteristic of R is positive, then the R-algebra A and the A-algebra B are the zero rings, where
$(p^j, g)$
forms a regular sequence on A and B. Since A is p-torsion-free and p-adically Zariskian, any prime number in A is a regular element. Thus, if the generic characteristic of R is positive, then the R-algebra A and the A-algebra B are the zero rings, where
![]() $(p^j, g)$
forms a regular sequence. If the generic characteristic of R is
$(p^j, g)$
forms a regular sequence. If the generic characteristic of R is
![]() $0$
, then R is N-2 by [Reference Ford18, Th. 4.6.10], and hence the assertion follows from Lemma 4.9, as desired. The assertion (c) follows from the assertion (b) and [Reference Scholze52, Th. 7.9]. Finally, let us prove the assertion (d). By assumption,
$0$
, then R is N-2 by [Reference Ford18, Th. 4.6.10], and hence the assertion follows from Lemma 4.9, as desired. The assertion (c) follows from the assertion (b) and [Reference Scholze52, Th. 7.9]. Finally, let us prove the assertion (d). By assumption,
![]() $A[\frac {p^{j}}{g}]$
and
$A[\frac {p^{j}}{g}]$
and
![]() $B[\frac {p^{j}}{g}]$
are integral over a Noetherian ring. Moreover, the ring map
$B[\frac {p^{j}}{g}]$
are integral over a Noetherian ring. Moreover, the ring map
![]() $A[\frac {p^{j}}{g}]\to B[\frac {p^{j}}{g}]$
is integral. Hence, by Proposition 7.1,
$A[\frac {p^{j}}{g}]\to B[\frac {p^{j}}{g}]$
is integral. Hence, by Proposition 7.1,
 $$ \begin{align*}B^{j\circ}=\biggl(B[\frac{p^{j}}{g}]\biggr)^{+}_{B^{j}}=\biggl(A[\frac{p^{j}}{g}]\biggr)^{+}_{B^{j}}=\biggl(\biggl(A[\frac{p^{j}}{g}]\biggr)^{+}_{A^{j}}\biggr)^{+}_{B^{j}}=(A^{j\circ})^{+}_{B^{j}}. \end{align*} $$
$$ \begin{align*}B^{j\circ}=\biggl(B[\frac{p^{j}}{g}]\biggr)^{+}_{B^{j}}=\biggl(A[\frac{p^{j}}{g}]\biggr)^{+}_{B^{j}}=\biggl(\biggl(A[\frac{p^{j}}{g}]\biggr)^{+}_{A^{j}}\biggr)^{+}_{B^{j}}=(A^{j\circ})^{+}_{B^{j}}. \end{align*} $$
Therefore, the first assertion follows. Thus, the second assertion follows from the almost purity theorem for Witt-perfect rings [Reference Davis and Kedlaya15, Th. 5.2] or [Reference Davis and Kedlaya16, Th. 2.9] (see [Reference Nakazato and Shimomoto45, Th. 5.9] for a conceptual proof).
(3): Since B is integral over A and
![]() $p\in A$
is contained in the Jacobson radical, it is also contained in the Jacobson radical of B. Moreover, B is integral over a Noetherian normal domain R, and integrally closed in
$p\in A$
is contained in the Jacobson radical, it is also contained in the Jacobson radical of B. Moreover, B is integral over a Noetherian normal domain R, and integrally closed in
![]() $B[\frac {1}{pg}]$
. Hence, we can apply Theorem 5.11 to B and obtain the assertion.
$B[\frac {1}{pg}]$
. Hence, we can apply Theorem 5.11 to B and obtain the assertion.
(4): The assertions (a) and (b) have already been proved above. Since B is integrally closed in
![]() $B[\frac {1}{pg}]$
, the assertion (c) follows from Proposition 7.1. Let us show the assertion (d). To prove the almost Witt-perfectness, it suffices to check that the condition (1) in Definition 5.2 is satisfied because B contains
$B[\frac {1}{pg}]$
, the assertion (c) follows from Proposition 7.1. Let us show the assertion (d). To prove the almost Witt-perfectness, it suffices to check that the condition (1) in Definition 5.2 is satisfied because B contains
![]() $p^{\frac {1}{p}}$
. By applying [Reference André1, Prop. 4.4.1] (see Corollary 8.2 for a self-contained proof), for any fixed
$p^{\frac {1}{p}}$
. By applying [Reference André1, Prop. 4.4.1] (see Corollary 8.2 for a self-contained proof), for any fixed
![]() $r=\frac {n}{p}$
with
$r=\frac {n}{p}$
with
![]() $n \in \mathbb {N}$
, we get a
$n \in \mathbb {N}$
, we get a
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism:
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism:
After applying
![]() $\varprojlim $
to the standard short exact sequence
$\varprojlim $
to the standard short exact sequence
![]() $0 \to B^{j\circ }/(p^{\frac {p-1}{p}}) \to B^{j\circ }/(p) \to B^{j\circ }/(p^{\frac {1}{p}}) \to 0$
, the following
$0 \to B^{j\circ }/(p^{\frac {p-1}{p}}) \to B^{j\circ }/(p) \to B^{j\circ }/(p^{\frac {1}{p}}) \to 0$
, the following
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost surjection follows from (5.28):
$(pg)^{\frac {1}{p^{\infty }}}$
-almost surjection follows from (5.28):
 $$ \begin{align} \varprojlim_j \big(B^{j\circ}/(p)\big) \to \varprojlim_j \big(B^{j\circ}/(p^{\frac{1}{p}})\big). \end{align} $$
$$ \begin{align} \varprojlim_j \big(B^{j\circ}/(p)\big) \to \varprojlim_j \big(B^{j\circ}/(p^{\frac{1}{p}})\big). \end{align} $$
By Witt-perfectness of
![]() $B^{j\circ }$
, the Frobenius isomorphism
$B^{j\circ }$
, the Frobenius isomorphism
![]() $B^{j\circ }/(p^{\frac {1}{p}}) \cong B^{j\circ }/(p)$
yields a short exact sequence:
$B^{j\circ }/(p^{\frac {1}{p}}) \cong B^{j\circ }/(p)$
yields a short exact sequence:
![]() $0 \to B^{j\circ }/(p^{\frac {1}{p}}) \to B^{j\circ }/(p) \xrightarrow {Frob} B^{j\circ }/(p) \to 0$
. Then again by (5.28), we get
$0 \to B^{j\circ }/(p^{\frac {1}{p}}) \to B^{j\circ }/(p) \xrightarrow {Frob} B^{j\circ }/(p) \to 0$
. Then again by (5.28), we get
 $$ \begin{align} \varprojlim_j \big(B^{j\circ}/(p)\big) \xrightarrow{Frob} \varprojlim_j \big(B^{j\circ}/(p)\big)~\mbox{is}~(pg)^{\frac{1}{p^{\infty}}}\mbox{-almost surjective}. \end{align} $$
$$ \begin{align} \varprojlim_j \big(B^{j\circ}/(p)\big) \xrightarrow{Frob} \varprojlim_j \big(B^{j\circ}/(p)\big)~\mbox{is}~(pg)^{\frac{1}{p^{\infty}}}\mbox{-almost surjective}. \end{align} $$
Consider the commutative diagram

It suffices to show that in view of (5.30) that
 $$ \begin{align} \big(\varprojlim_j B^{j\circ}\big)/(p) \to \varprojlim_j \big(B^{j\circ}/(p)\big)~\mbox{is a}~(pg)^{\frac{1}{p^{\infty}}}\mbox{-almost isomorphism}. \end{align} $$
$$ \begin{align} \big(\varprojlim_j B^{j\circ}\big)/(p) \to \varprojlim_j \big(B^{j\circ}/(p)\big)~\mbox{is a}~(pg)^{\frac{1}{p^{\infty}}}\mbox{-almost isomorphism}. \end{align} $$
By taking the inverse limits over j to the short exact sequence:
![]() $0 \to B^{j\circ } \xrightarrow {p} B^{j\circ } \to B^{j\circ }/ (p) \to 0$
, we see that the map in (5.31) is injective. On the other hand, the above map is
$0 \to B^{j\circ } \xrightarrow {p} B^{j\circ } \to B^{j\circ }/ (p) \to 0$
, we see that the map in (5.31) is injective. On the other hand, the above map is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective by applying the almost surjectivity of (5.29) to [Reference André1, Prop. 4.3.1 and remarque 4.3.1], which shows that the Frobenius endomorphism on
$(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective by applying the almost surjectivity of (5.29) to [Reference André1, Prop. 4.3.1 and remarque 4.3.1], which shows that the Frobenius endomorphism on
![]() $(\varprojlim _{j}{B^{j\circ }})/(p)$
is
$(\varprojlim _{j}{B^{j\circ }})/(p)$
is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective. Hence, by the assertion (3), we obtain the desired consequence.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost surjective. Hence, by the assertion (3), we obtain the desired consequence.
(5): It follows from the assertions (3) and (4).
Let us complete the proof of Theorem 5.20.
Proof of Theorem 5.20
The assertion (a) follows from the assertions (c) and (d) of Proposition 5.21(4). Let us prove the assertion (b). We fix the notation as in Proposition 5.21. Let us make a reduction by using Galois theory of rings. By decomposing A into the direct product of rings, we may assume and do that
![]() $A[\frac {1}{pg}] \to B'$
is finite étale of constant rank (indeed, one can check the conditions (1)–(4) remain to hold for each direct factor of the ring A). By Lemma 9.4 applied to the finite étale extension
$A[\frac {1}{pg}] \to B'$
is finite étale of constant rank (indeed, one can check the conditions (1)–(4) remain to hold for each direct factor of the ring A). By Lemma 9.4 applied to the finite étale extension
![]() $A[\frac {1}{pg}] \hookrightarrow B'=B[\frac {1}{pg}]$
, there is the decomposition
$A[\frac {1}{pg}] \hookrightarrow B'=B[\frac {1}{pg}]$
, there is the decomposition
 $$ \begin{align} A[\frac{1}{pg}] \hookrightarrow B'=B[\frac{1}{pg}] \hookrightarrow C', \end{align} $$
$$ \begin{align} A[\frac{1}{pg}] \hookrightarrow B'=B[\frac{1}{pg}] \hookrightarrow C', \end{align} $$
where
![]() $A[\frac {1}{pg}] \to C'$
and
$A[\frac {1}{pg}] \to C'$
and
![]() $B'=B[\frac {1}{pg}] \to C'$
are Galois coverings. Let G be the Galois group for
$B'=B[\frac {1}{pg}] \to C'$
are Galois coverings. Let G be the Galois group for
![]() $A[\frac {1}{pg}] \to C'$
and let
$A[\frac {1}{pg}] \to C'$
and let
![]() $H \subset G$
be the Galois subgroup for
$H \subset G$
be the Galois subgroup for
![]() $B' \to C'$
. Notice that G is finite. Let C be the integral closure of A in
$B' \to C'$
. Notice that G is finite. Let C be the integral closure of A in
![]() $C'$
. Notice that one can apply Proposition 5.21 to A and C by taking
$C'$
. Notice that one can apply Proposition 5.21 to A and C by taking
![]() $B'=A[\frac {1}{pg}]$
and
$B'=A[\frac {1}{pg}]$
and
![]() $B'=C'$
, respectively (cf. Proposition 5.21(1)). We will use the consequences of this fact without explicit mention in what follows.
$B'=C'$
, respectively (cf. Proposition 5.21(1)). We will use the consequences of this fact without explicit mention in what follows.
In view of (5.5) and Proposition 5.21(2)-(a), we obtain the following commutative diagram:

Taking inverse limits, we have composite map of rings:
 $$ \begin{align} A \cong \widetilde{A}:=\varprojlim_j A^{j\circ} \to \widetilde{B}:=\varprojlim_j B^{j\circ} \to B', \end{align} $$
$$ \begin{align} A \cong \widetilde{A}:=\varprojlim_j A^{j\circ} \to \widetilde{B}:=\varprojlim_j B^{j\circ} \to B', \end{align} $$
where the first isomorphism is due to Theorem 5.11. Similarly, we obtain the compositions of ring maps:
 $$ \begin{align} A \cong\widetilde{A} \to \widetilde{C}:=\varprojlim_j C^{j\circ} \to C'. \end{align} $$
$$ \begin{align} A \cong\widetilde{A} \to \widetilde{C}:=\varprojlim_j C^{j\circ} \to C'. \end{align} $$
By Proposition 5.21(3), we find that (5.33) and (5.34) are isomorphic to the integral maps
![]() $A\to B$
and
$A\to B$
and
![]() $A \to C$
, respectively. Following the convention in Definition 5.12, we set
$A \to C$
, respectively. Following the convention in Definition 5.12, we set
 $$ \begin{align*}\mathcal{B}:=\widehat{B}[\frac{1}{p}]~\mbox{and}~\mathcal{C}:=\widehat{C}[\frac{1}{p}]. \end{align*} $$
$$ \begin{align*}\mathcal{B}:=\widehat{B}[\frac{1}{p}]~\mbox{and}~\mathcal{C}:=\widehat{C}[\frac{1}{p}]. \end{align*} $$
Our goal is the following:
-
• Recall that
 $A[\frac {1}{pg}] \to C'$
is a G-Galois covering and
$A[\frac {1}{pg}] \to C'$
is a G-Galois covering and
 $B'=B[\frac {1}{pg}] \to C'$
is a H-Galois covering. Fix an integer
$B'=B[\frac {1}{pg}] \to C'$
is a H-Galois covering. Fix an integer
 $m>0$
. Then we will establish that
$m>0$
. Then we will establish that
 $A/(p^m) \to C/(p^m)$
is a
$A/(p^m) \to C/(p^m)$
is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost G-Galois covering, and
$(pg)^{\frac {1}{p^{\infty }}}$
-almost G-Galois covering, and
 $B/(p^m) \to C/(p^m)$
is a
$B/(p^m) \to C/(p^m)$
is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost H-Galois covering. Using these facts combined with Proposition 9.3(3), we deduce that
$(pg)^{\frac {1}{p^{\infty }}}$
-almost H-Galois covering. Using these facts combined with Proposition 9.3(3), we deduce that
 $A/(p^m) \to B/(p^m)$
is
$A/(p^m) \to B/(p^m)$
is
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale. As we can treat
$(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale. As we can treat
 $A \to C$
and
$A \to C$
and
 $B \to C$
in a complete parallel manner in view of Proposition 5.21, we consider only the case
$B \to C$
in a complete parallel manner in view of Proposition 5.21, we consider only the case
 $A \to C$
in what follows. We use the notation
$A \to C$
in what follows. We use the notation
 $A \to C$
and
$A \to C$
and
 $\widetilde {A} \to \widetilde {C}$
interchangeably.
$\widetilde {A} \to \widetilde {C}$
interchangeably.
As
![]() $A[\frac {1}{pg}] \to C'$
is a G-Galois covering, so is
$A[\frac {1}{pg}] \to C'$
is a G-Galois covering, so is
![]() $\mathcal {A}^j\to \mathcal {C}^j$
in view of [Reference Ford18, Lem. 12.2.7]. Let
$\mathcal {A}^j\to \mathcal {C}^j$
in view of [Reference Ford18, Lem. 12.2.7]. Let
![]() $\widehat {C^{j\circ }}$
be the p-adic completion of
$\widehat {C^{j\circ }}$
be the p-adic completion of
![]() $C^{j\circ }$
. Since
$C^{j\circ }$
. Since
![]() $C^{j\circ }[\frac {1}{p}]=C'$
, there is a natural
$C^{j\circ }[\frac {1}{p}]=C'$
, there is a natural
![]() $\mathcal {A}^j$
-algebra map
$\mathcal {A}^j$
-algebra map
 $$ \begin{align} \mathcal{C}^j=C' \otimes_{A[\frac{1}{pg}]} \mathcal{A}^j \to \widehat{C^{j\circ}}[\frac{1}{p}]. \end{align} $$
$$ \begin{align} \mathcal{C}^j=C' \otimes_{A[\frac{1}{pg}]} \mathcal{A}^j \to \widehat{C^{j\circ}}[\frac{1}{p}]. \end{align} $$
Since
![]() $\widehat {A^{j\circ }}\cong \mathcal {A}^{j\circ }$
by Proposition 5.15(4), the map (5.35) is an isomorphism, which induces
$\widehat {A^{j\circ }}\cong \mathcal {A}^{j\circ }$
by Proposition 5.15(4), the map (5.35) is an isomorphism, which induces
![]() $\mathcal {C}^{j\circ } \cong \widehat {C^{j\circ }}$
in view of [Reference Nakazato and Shimomoto45, Cor. 4.10]. Thus, G acts on
$\mathcal {C}^{j\circ } \cong \widehat {C^{j\circ }}$
in view of [Reference Nakazato and Shimomoto45, Cor. 4.10]. Thus, G acts on
![]() $\widehat {C^{j\circ }}$
and
$\widehat {C^{j\circ }}$
and
by applying Lemma 4.5 or Discussion 5.22(1). In particular,
![]() $\mathcal {A}^{j\circ } \to \widehat {C^{j\circ }}$
is an integral extension. In summary,
$\mathcal {A}^{j\circ } \to \widehat {C^{j\circ }}$
is an integral extension. In summary,
 $$ \begin{align} \mathcal{A}^{j\circ} \to \mathcal{C}^{j\circ} \cong \widehat{C^{j\circ}}~\mbox{is}~(p)^{\frac{1}{p^{\infty}}}\mbox{-almost} \ \acute{\rm e}\mbox{tale and}~\mathcal{A}^j \to \mathcal{C}^j \cong \widehat{C^{j\circ}}[\frac{1}{p}]~\mbox{is a}~G\mbox{-Galois covering}. \end{align} $$
$$ \begin{align} \mathcal{A}^{j\circ} \to \mathcal{C}^{j\circ} \cong \widehat{C^{j\circ}}~\mbox{is}~(p)^{\frac{1}{p^{\infty}}}\mbox{-almost} \ \acute{\rm e}\mbox{tale and}~\mathcal{A}^j \to \mathcal{C}^j \cong \widehat{C^{j\circ}}[\frac{1}{p}]~\mbox{is a}~G\mbox{-Galois covering}. \end{align} $$
To finish the proof, let us apply the proof of [Reference André1, Prop. 5.2.3] via Galois theory of commutative rings to (5.37). We refer the reader to [Reference André1, (5.6)–(5.10) of Prop. 5.2.3] for the following discussions.
After invoking the notation (5.33) and (5.34), there follows the following
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms by applying Theorem 5.16(b) to
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms by applying Theorem 5.16(b) to
![]() $A^j$
(resp.
$A^j$
(resp.
![]() $C^j$
):
$C^j$
):
Indeed, this is checked by a chain of almost isomorphisms:
 $$ \begin{align*}\widehat{\widetilde{A}} \cong \widehat{\varprojlim_j A^{j\circ}} \approx \varprojlim_j \widehat{A^{j\circ}} \cong g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ} \approx \mathcal{A}^{\circ}. \end{align*} $$
$$ \begin{align*}\widehat{\widetilde{A}} \cong \widehat{\varprojlim_j A^{j\circ}} \approx \varprojlim_j \widehat{A^{j\circ}} \cong g^{-\frac{1}{p^{\infty}}}\mathcal{A}^{\circ} \approx \mathcal{A}^{\circ}. \end{align*} $$
Here, the first isomorphism is the p-adic completion of the isomorphism from Theorem 5.11, and the last second isomorphism is due to Riemann’s extension theorem [Reference André1, théorème 4.2.2] (see Theorem 8.1 for a self-contained proof). The same reasoning applies to deduce
![]() $\widehat {\widetilde {C}} \approx \mathcal {C}^{\circ }$
.
$\widehat {\widetilde {C}} \approx \mathcal {C}^{\circ }$
.
In view of (5.37) and applying [Reference André1, Prop. 3.3.4], the ring map
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism, where the completed tensor product is p-adic. By [Reference André1, Prop. 4.4.4], we have
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism, where the completed tensor product is p-adic. By [Reference André1, Prop. 4.4.4], we have
![]() $\mathcal {C}\{\frac {p^j}{g}\} \cong \mathcal {C}^j$
and
$\mathcal {C}\{\frac {p^j}{g}\} \cong \mathcal {C}^j$
and
![]() $\mathcal {C}$
is an
$\mathcal {C}$
is an
![]() $\mathcal {A}$
-algebra. Using this, we obtain
$\mathcal {A}$
-algebra. Using this, we obtain
 $$ \begin{align*}\big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{C}\big)\{\frac{p^j}{g}\} \cong \mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{A}^j \cong \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{A}^j\big) \otimes_{\mathcal{A}^j} \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{A}^j\big) \cong \mathcal{C}\{\frac{p^j}{g}\} \otimes_{\mathcal{A}^j} \mathcal{C}\{\frac{p^j}{g}\}\cong \mathcal{C}^j \otimes_{\mathcal{A}^j}\mathcal{C}^j. \end{align*} $$
$$ \begin{align*}\big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{C}\big)\{\frac{p^j}{g}\} \cong \mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{A}^j \cong \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{A}^j\big) \otimes_{\mathcal{A}^j} \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{A}^j\big) \cong \mathcal{C}\{\frac{p^j}{g}\} \otimes_{\mathcal{A}^j} \mathcal{C}\{\frac{p^j}{g}\}\cong \mathcal{C}^j \otimes_{\mathcal{A}^j}\mathcal{C}^j. \end{align*} $$
By Riemann’s extension theorem [Reference André1, théorème 4.2.2] (see also Theorem 8.1) and by [Reference André1, Prop. 3.3.4], we have
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms:
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms:
 $$ \begin{align} \varprojlim_j \big(\mathcal{C}^{j\circ} \widehat{\otimes}_{\mathcal{A}^{j\circ}}\mathcal{C}^{j\circ}\big) \approx \varprojlim_j \big(\mathcal{C}^j \otimes_{\mathcal{A}^j}\mathcal{C}^j\big)^{\circ} \cong \varprojlim_j \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{C}\big)\{\frac{p^j}{g}\}^{\circ} \approx \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}}\mathcal{C}\big)^{\circ} \approx \mathcal{C}^{\circ} \widehat{\otimes}_{\mathcal{A}^{\circ}} \mathcal{C}^{\circ}. \end{align} $$
$$ \begin{align} \varprojlim_j \big(\mathcal{C}^{j\circ} \widehat{\otimes}_{\mathcal{A}^{j\circ}}\mathcal{C}^{j\circ}\big) \approx \varprojlim_j \big(\mathcal{C}^j \otimes_{\mathcal{A}^j}\mathcal{C}^j\big)^{\circ} \cong \varprojlim_j \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}} \mathcal{C}\big)\{\frac{p^j}{g}\}^{\circ} \approx \big(\mathcal{C} \widehat{\otimes}_{\mathcal{A}}\mathcal{C}\big)^{\circ} \approx \mathcal{C}^{\circ} \widehat{\otimes}_{\mathcal{A}^{\circ}} \mathcal{C}^{\circ}. \end{align} $$
Putting (5.39) and (5.40) together, we obtain the following
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism:
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism:
By Discussion 5.22(2), we know that
![]() $\mathcal {A}^{\circ }/(p^m) \to \big (\mathcal {C}^{\circ }/(p^m)\big )^G$
is a
$\mathcal {A}^{\circ }/(p^m) \to \big (\mathcal {C}^{\circ }/(p^m)\big )^G$
is a
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism for any
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism for any
![]() $m>0$
. So this fact combined with the
$m>0$
. So this fact combined with the
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms (5.38) and (5.41) modulo
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms (5.38) and (5.41) modulo
![]() $p^m$
yields that the induced map:
$p^m$
yields that the induced map:
![]() $\widetilde {A}/(p^m) \to \widetilde {C}/(p^m)$
is a
$\widetilde {A}/(p^m) \to \widetilde {C}/(p^m)$
is a
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost G-Galois covering. This map factors as
$(pg)^{\frac {1}{p^{\infty }}}$
-almost G-Galois covering. This map factors as
![]() $\widetilde {A}/(p^m) \to \widetilde {B}/(p^m) \to \widetilde {C}/(p^m)$
. It then follows from Proposition 9.3(3) that
$\widetilde {A}/(p^m) \to \widetilde {B}/(p^m) \to \widetilde {C}/(p^m)$
. It then follows from Proposition 9.3(3) that
![]() $\widetilde {A}/(p^m) \to \widetilde {B}/(p^m)$
is
$\widetilde {A}/(p^m) \to \widetilde {B}/(p^m)$
is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale, as desired. This completes the proof of the theorem.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale, as desired. This completes the proof of the theorem.
Discussion 5.22.
-
1. Here is a way to check the isomorphism:
 $(\widehat {C^{j\circ }})^G \cong \mathcal {A}^{j\circ }$
that appears in (5.36). Since inverse limits commutes with taking G-invariants and
$(\widehat {C^{j\circ }})^G \cong \mathcal {A}^{j\circ }$
that appears in (5.36). Since inverse limits commutes with taking G-invariants and
 $\widehat {A^{j\circ }} \cong \mathcal {A}^{j\circ }$
by Proposition 5.15, we have (5.42)where
$\widehat {A^{j\circ }} \cong \mathcal {A}^{j\circ }$
by Proposition 5.15, we have (5.42)where $$ \begin{align} \kern-12pt(\widehat{C^{j\circ}})^G \cong \big(\varprojlim_m C^{j\circ}/(p^m)\big)^G \cong \varprojlim_m \big(C^{j\circ}/(p^m)\big)^G \approx \varprojlim_m \big((C^{j\circ})^G/(p^m)\big) \cong \varprojlim_m A^{j\circ}/(p^m) \cong \mathcal{A}^{j\circ}, \end{align} $$
$$ \begin{align} \kern-12pt(\widehat{C^{j\circ}})^G \cong \big(\varprojlim_m C^{j\circ}/(p^m)\big)^G \cong \varprojlim_m \big(C^{j\circ}/(p^m)\big)^G \approx \varprojlim_m \big((C^{j\circ})^G/(p^m)\big) \cong \varprojlim_m A^{j\circ}/(p^m) \cong \mathcal{A}^{j\circ}, \end{align} $$
 $\approx $
in the middle denotes a
$\approx $
in the middle denotes a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism and we reason this as follows: Consider the short exact sequence
$(p)^{\frac {1}{p^{\infty }}}$
-almost isomorphism and we reason this as follows: Consider the short exact sequence
 $0 \to C^{j\circ } \xrightarrow {p^m} C^{j\circ } \to C^{j\circ }/(p^m) \to 0$
. Applying the Galois cohomology
$0 \to C^{j\circ } \xrightarrow {p^m} C^{j\circ } \to C^{j\circ }/(p^m) \to 0$
. Applying the Galois cohomology
 $H^i(G,~)$
to this exact sequence, we get an injection
$H^i(G,~)$
to this exact sequence, we get an injection
 $(C^{j\circ })^G/(p^m) \hookrightarrow \big (C^{j\circ }/(p^m)\big )^G$
whose cokernel embeds into
$(C^{j\circ })^G/(p^m) \hookrightarrow \big (C^{j\circ }/(p^m)\big )^G$
whose cokernel embeds into
 $H^1(G,C^{j\circ })$
. By applying [Reference Faltings17, Th. 2.4] or [Reference Olsson46, Prop. 3.4],
$H^1(G,C^{j\circ })$
. By applying [Reference Faltings17, Th. 2.4] or [Reference Olsson46, Prop. 3.4],
 $H^1(G,C^{j\circ })$
is
$H^1(G,C^{j\circ })$
is
 $(p)^{\frac {1}{p^{\infty }}}$
-almost zero. Hence (5.42) is proved.
$(p)^{\frac {1}{p^{\infty }}}$
-almost zero. Hence (5.42) is proved.
 $\widehat {C^{j\circ }}$
is completely integrally closed in
$\widehat {C^{j\circ }}$
is completely integrally closed in
 $\widehat {C^{j\circ }}[\frac {1}{p}]$
by Lemma 3.3. Then we have
$\widehat {C^{j\circ }}[\frac {1}{p}]$
by Lemma 3.3. Then we have
 $\widehat {C^{j\circ }} \cong p^{-\frac {1}{p^{\infty }}}(\widehat {C^{j\circ }})$
and
$\widehat {C^{j\circ }} \cong p^{-\frac {1}{p^{\infty }}}(\widehat {C^{j\circ }})$
and
 $p^{-\frac {1}{p^{\infty }}}(\mathcal {A}^{j\circ }) \cong \mathcal {A}^{j\circ }$
by Lemma 3.5. Since the functor
$p^{-\frac {1}{p^{\infty }}}(\mathcal {A}^{j\circ }) \cong \mathcal {A}^{j\circ }$
by Lemma 3.5. Since the functor
 $p^{-\frac {1}{p^{\infty }}}(~)$
commutes with taking G-invariants, (5.42) yields an (honest) isomorphism: which proves (5.36).
$p^{-\frac {1}{p^{\infty }}}(~)$
commutes with taking G-invariants, (5.42) yields an (honest) isomorphism: which proves (5.36). $$ \begin{align*}(\widehat{C^{j\circ}})^G \cong \big(p^{-\frac{1}{p^{\infty}}}(\widehat{C^{j\circ}})\big)^G \cong p^{-\frac{1}{p^{\infty}}}\big((\widehat{C^{j\circ}})^G\big) \cong p^{-\frac{1}{p^{\infty}}}(\mathcal{A}^{j\circ}) \cong \mathcal{A}^{j\circ}, \end{align*} $$
$$ \begin{align*}(\widehat{C^{j\circ}})^G \cong \big(p^{-\frac{1}{p^{\infty}}}(\widehat{C^{j\circ}})\big)^G \cong p^{-\frac{1}{p^{\infty}}}\big((\widehat{C^{j\circ}})^G\big) \cong p^{-\frac{1}{p^{\infty}}}(\mathcal{A}^{j\circ}) \cong \mathcal{A}^{j\circ}, \end{align*} $$
-
2. Using (5.36), let us prove that the map
is a $$ \begin{align*} \mathcal{A}^{\circ}/(p^m) \to\big(\mathcal{C}^{\circ}/(p^m)\big)^G \end{align*} $$
$$ \begin{align*} \mathcal{A}^{\circ}/(p^m) \to\big(\mathcal{C}^{\circ}/(p^m)\big)^G \end{align*} $$
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism for any integer
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphism for any integer
 $m>0$
. We have already seen the
$m>0$
. We have already seen the
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms:
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms:
 $\mathcal {A}^{j\circ }/(p^m) \approx (\mathcal {C}^{j\circ })^G/(p^m) \approx \big (\mathcal {C}^{j\circ }/(p^m)\big )^G$
. Taking the inverse limits
$\mathcal {A}^{j\circ }/(p^m) \approx (\mathcal {C}^{j\circ })^G/(p^m) \approx \big (\mathcal {C}^{j\circ }/(p^m)\big )^G$
. Taking the inverse limits
 $j \to \infty $
and using [Reference André1, Prop. 4.2.1] or the
$j \to \infty $
and using [Reference André1, Prop. 4.2.1] or the
 $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism (8.1), we get
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism (8.1), we get
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms: as wanted.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphisms: as wanted. $$ \begin{align*}\mathcal{A}^{\circ}/(p^m) \approx \varprojlim_{j>0} \big(\mathcal{C}^{j\circ}/(p^m)\big)^G \cong \big(\varprojlim_{j>0} \mathcal{C}^{j\circ}/(p^m)\big)^G \approx \big(\mathcal{C}^{\circ}/(p^m)\big)^G, \end{align*} $$
$$ \begin{align*}\mathcal{A}^{\circ}/(p^m) \approx \varprojlim_{j>0} \big(\mathcal{C}^{j\circ}/(p^m)\big)^G \cong \big(\varprojlim_{j>0} \mathcal{C}^{j\circ}/(p^m)\big)^G \approx \big(\mathcal{C}^{\circ}/(p^m)\big)^G, \end{align*} $$
Problem 2. Does Theorem 5.20 hold true under the more general assumption that A is not necessarily integral over a Noetherian ring?
This problem is related to a possible generalization of Riemann’s extension theorem (see Theorems 5.11 and 5.16) for Witt-perfect rings of general type.
6 Applications of Witt-perfect Abhyankar’s lemma
6.1 A construction of almost Cohen–Macaulay algebras
Before proving the main theorem for this section, we recall the definition of big Cohen–Macaulay algebras, due to Hochster.
Definition 6.1 (Big Cohen–Macaulay algebra)
Let
![]() $(R,\frak {m})$
be a Noetherian local ring of dimension
$(R,\frak {m})$
be a Noetherian local ring of dimension
![]() $d>0$
, and let T be an R-algebra. Then T is a big Cohen–Macaulay R-algebra, if there is a system of parameters
$d>0$
, and let T be an R-algebra. Then T is a big Cohen–Macaulay R-algebra, if there is a system of parameters
![]() $x_1,\ldots ,x_d$
such that
$x_1,\ldots ,x_d$
such that
![]() $x_1,\ldots ,x_d$
is a regular sequence on T and
$x_1,\ldots ,x_d$
is a regular sequence on T and
![]() $(x_1,\ldots ,x_d)T \ne T$
. Moreover, we say that a big Cohen–Macaulay algebra is balanced, if every system of parameters satisfies the above conditions.
$(x_1,\ldots ,x_d)T \ne T$
. Moreover, we say that a big Cohen–Macaulay algebra is balanced, if every system of parameters satisfies the above conditions.
We also recall the definition of almost Cohen–Macaulay algebras from [Reference André2, Defn. 4.1.1]. Refer the reader to [Reference André3, Prop. 2.5.1] for a subtle point on this definition.
Definition 6.2 (Almost Cohen–Macaulay algebra)
Let
![]() $(R,\frak {m})$
be a Noetherian local ring of dimension
$(R,\frak {m})$
be a Noetherian local ring of dimension
![]() $d>0$
, and let
$d>0$
, and let
![]() $(T,I)$
be a basic setup equipped with an R-algebra structure. Fix a system of parameters
$(T,I)$
be a basic setup equipped with an R-algebra structure. Fix a system of parameters
![]() $x_1,\ldots ,x_d$
. We say that T is I-almost Cohen–Macaulay with respect to
$x_1,\ldots ,x_d$
. We say that T is I-almost Cohen–Macaulay with respect to
![]() $x_1,\ldots ,x_d$
, if
$x_1,\ldots ,x_d$
, if
![]() $T/\frak {m} T$
is not I-almost zero and
$T/\frak {m} T$
is not I-almost zero and
for any
![]() $c \in I$
and
$c \in I$
and
![]() $i=0,\ldots ,d-1$
.
$i=0,\ldots ,d-1$
.
It is important to keep in mind that the permutation of the sequence
![]() $x_1,\ldots ,x_d$
in the above definition may fail to form an almost regular sequence. We consider the sequence
$x_1,\ldots ,x_d$
in the above definition may fail to form an almost regular sequence. We consider the sequence
![]() $p,x_2,\ldots ,x_d$
for the main theorem below.
$p,x_2,\ldots ,x_d$
for the main theorem below.
André’s construction: For the applications given below, we take I to be the ideal
![]() $\bigcup _{n>0} \varpi ^{\frac {1}{p^n}}T$
as the basic setup
$\bigcup _{n>0} \varpi ^{\frac {1}{p^n}}T$
as the basic setup
![]() $(T,I)$
for some regular element
$(T,I)$
for some regular element
![]() $\varpi \in R$
. Following [Reference André2], we introduce some auxiliary algebras. Let
$\varpi \in R$
. Following [Reference André2], we introduce some auxiliary algebras. Let
![]() $W(k)$
be the ring of Witt vectors for a perfect field k of characteristic
$W(k)$
be the ring of Witt vectors for a perfect field k of characteristic
![]() $p>0$
, and let
$p>0$
, and let
be an unramified complete regular local ring and
![]() $V_j:=W(k)[p^{\frac {1}{p^j}}]$
. Then
$V_j:=W(k)[p^{\frac {1}{p^j}}]$
. Then
![]() $V_j$
is a complete discrete valuation ring and set
$V_j$
is a complete discrete valuation ring and set
![]() $V_{\infty }:=\varinjlim _j V_j$
. Then this is a Witt-perfect valuation domain. For a fixed element
$V_{\infty }:=\varinjlim _j V_j$
. Then this is a Witt-perfect valuation domain. For a fixed element
![]() $0 \ne g \in A$
, we set
$0 \ne g \in A$
, we set
 $$ \begin{align*}B_{jk}:=V_j[[x^{\frac{1}{p^j}}_2,\ldots,x^{\frac{1}{p^j}}_d]][g^{\frac{1}{p^k}}][\frac{1}{p}]:=\Big(V_j[[x^{\frac{1}{p^j}}_2,\ldots,x^{\frac{1}{p^j}}_d]][T]/(T^{p^k}-g)\Big)[\frac{1}{p}] \end{align*} $$
$$ \begin{align*}B_{jk}:=V_j[[x^{\frac{1}{p^j}}_2,\ldots,x^{\frac{1}{p^j}}_d]][g^{\frac{1}{p^k}}][\frac{1}{p}]:=\Big(V_j[[x^{\frac{1}{p^j}}_2,\ldots,x^{\frac{1}{p^j}}_d]][T]/(T^{p^k}-g)\Big)[\frac{1}{p}] \end{align*} $$
for any pair of nonnegative integers
![]() $(j,k)$
. For any pairs
$(j,k)$
. For any pairs
![]() $(j,k)$
and
$(j,k)$
and
![]() $(j',k')$
with
$(j',k')$
with
![]() $j \le j'$
and
$j \le j'$
and
![]() $k \le k'$
, we can define the natural map
$k \le k'$
, we can define the natural map
![]() $B_{jk} \to B_{j'k'}$
. Let us define the A-algebra
$B_{jk} \to B_{j'k'}$
. Let us define the A-algebra
![]() $A_{jk}$
to be the integral closure of A in
$A_{jk}$
to be the integral closure of A in
![]() $B_{jk}$
. Let us also define
$B_{jk}$
. Let us also define
 $$ \begin{align} A_{\infty\infty}:=\varinjlim_{j,k} A_{jk}~\mbox{and}~A_{\infty g}:=\mbox{the integral closure of}~A_{\infty\infty}~\mbox{in}~A_{\infty\infty}[\frac{1}{pg}]. \end{align} $$
$$ \begin{align} A_{\infty\infty}:=\varinjlim_{j,k} A_{jk}~\mbox{and}~A_{\infty g}:=\mbox{the integral closure of}~A_{\infty\infty}~\mbox{in}~A_{\infty\infty}[\frac{1}{pg}]. \end{align} $$
For brevity, let us write
 $$ \begin{align} A_{\infty}:=A_{\infty0}:=\varinjlim_jV_j[[x^{\frac{1}{p^j}}_2,\ldots,x^{\frac{1}{p^j}}_d]]. \end{align} $$
$$ \begin{align} A_{\infty}:=A_{\infty0}:=\varinjlim_jV_j[[x^{\frac{1}{p^j}}_2,\ldots,x^{\frac{1}{p^j}}_d]]. \end{align} $$
Then we have a tower of integral ring maps:
Lemma 6.3. Let R be a Noetherian domain with a proper ideal I, and let T be a normal ring that is a torsion-free integral extension of R. Assume that
![]() $\varpi \in I$
is a nonzero element such that T admits a compatible system of p-power roots
$\varpi \in I$
is a nonzero element such that T admits a compatible system of p-power roots
![]() $\varpi ^{\frac {1}{p^n}}$
. Then
$\varpi ^{\frac {1}{p^n}}$
. Then
![]() $T/IT$
is not
$T/IT$
is not
![]() $(\varpi ^{\frac {1}{p^{\infty }}})$
-almost zero.
$(\varpi ^{\frac {1}{p^{\infty }}})$
-almost zero.
Proof. In order to prove that
![]() $T/IT$
is not
$T/IT$
is not
![]() $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost zero, it suffices to prove that
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost zero, it suffices to prove that
![]() $T_{\frak {m}}/IT_{\frak {m}}$
is not
$T_{\frak {m}}/IT_{\frak {m}}$
is not
![]() $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost zero, where
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost zero, where
![]() $\frak {m}$
is any maximal ideal of T containing
$\frak {m}$
is any maximal ideal of T containing
![]() $IT$
, since
$IT$
, since
![]() $T_{\frak {m}}/IT_{\frak {m}}$
is the localization of
$T_{\frak {m}}/IT_{\frak {m}}$
is the localization of
![]() $T/IT$
. Then
$T/IT$
. Then
![]() $T_{\frak {m}}$
is a normal domain that is an integral extension over the Noetherian domain
$T_{\frak {m}}$
is a normal domain that is an integral extension over the Noetherian domain
![]() $R_{\frak {m} \cap R}$
, in which I is a proper ideal. To derive a contradiction, we suppose that
$R_{\frak {m} \cap R}$
, in which I is a proper ideal. To derive a contradiction, we suppose that
![]() $T_{\frak {m}}/I T_{\frak {m}}$
is
$T_{\frak {m}}/I T_{\frak {m}}$
is
![]() $(\varpi ^{\frac {1}{p^{\infty }}})$
-almost zero. Notice that
$(\varpi ^{\frac {1}{p^{\infty }}})$
-almost zero. Notice that
![]() $T_{\frak {m}}$
is contained in the absolute integral closure
$T_{\frak {m}}$
is contained in the absolute integral closure
![]() $(R_{\frak {m} \cap R})^+$
. In particular, it implies that
$(R_{\frak {m} \cap R})^+$
. In particular, it implies that
Raising
![]() $p^n$
th power on both sides, we get by [Reference Shimomoto54, Lem. 4.2];
$p^n$
th power on both sides, we get by [Reference Shimomoto54, Lem. 4.2];
 $$ \begin{align*}\varpi \in \bigcap_{n>0} I^{p^n}T_{\frak{m}}=0, \end{align*} $$
$$ \begin{align*}\varpi \in \bigcap_{n>0} I^{p^n}T_{\frak{m}}=0, \end{align*} $$
which is a contradiction.
The big rings
![]() $A_{\infty \infty }$
and
$A_{\infty \infty }$
and
![]() $A_{\infty g}$
enjoy the following desirable properties.
$A_{\infty g}$
enjoy the following desirable properties.
Proposition 6.4. Let the notation be as in (6.1) and (6.2). Then the following assertions hold:
-
1.
 $A_{\infty }$
is completely integrally closed in its field of fractions. It is an integral and faithfully flat extension over A. Moreover, the localization map
$A_{\infty }$
is completely integrally closed in its field of fractions. It is an integral and faithfully flat extension over A. Moreover, the localization map
 $A_{\infty }[\frac {1}{pg}] \to A_{\infty \infty }[\frac {1}{pg}]$
is ind-étale. Finally,
$A_{\infty }[\frac {1}{pg}] \to A_{\infty \infty }[\frac {1}{pg}]$
is ind-étale. Finally,
 $A_{\infty \infty }$
is a
$A_{\infty \infty }$
is a
 $(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay and Witt-perfect algebra.
$(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay and Witt-perfect algebra. -
2.
 $A_{\infty g}$
is a
$A_{\infty g}$
is a
 $(g)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect algebra over the Witt-perfect valuation domain
$(g)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect algebra over the Witt-perfect valuation domain
 $V_{\infty }$
such that
$V_{\infty }$
such that
 $p^{\frac {1}{p^n}} \in V_{\infty }$
and
$p^{\frac {1}{p^n}} \in V_{\infty }$
and
 $g^{\frac {1}{p^n}} \in A_{\infty g}$
. Moreover,
$g^{\frac {1}{p^n}} \in A_{\infty g}$
. Moreover,
 $A_{\infty g}$
is a
$A_{\infty g}$
is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal ring that is completely integrally closed in
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal ring that is completely integrally closed in
 $A_{\infty g}[\frac {1}{pg}]$
. In particular, the localization of
$A_{\infty g}[\frac {1}{pg}]$
. In particular, the localization of
 $A_{\infty g}$
at any maximal ideal is a
$A_{\infty g}$
at any maximal ideal is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal domain.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal domain.
Proof.
![]() $(1)$
: It is clear that
$(1)$
: It is clear that
![]() $A \to A_{\infty }$
is integral by construction. Since
$A \to A_{\infty }$
is integral by construction. Since
![]() $A_{\infty }$
is a filtered colimit of regular local subrings with module-finite transition maps, one readily checks that the transition map is flat and thus,
$A_{\infty }$
is a filtered colimit of regular local subrings with module-finite transition maps, one readily checks that the transition map is flat and thus,
![]() $A \to A_{\infty }$
is faithfully flat. By Lemma 3.8,
$A \to A_{\infty }$
is faithfully flat. By Lemma 3.8,
![]() $A_{\infty }$
is a completely integrally closed domain in its field of fractions. By looking at the discriminant, it is easy to check that
$A_{\infty }$
is a completely integrally closed domain in its field of fractions. By looking at the discriminant, it is easy to check that
![]() $A_{\infty }[\frac {1}{pg}] \to A_{\infty \infty }[\frac {1}{pg}]$
is ind-étale. We claim that
$A_{\infty }[\frac {1}{pg}] \to A_{\infty \infty }[\frac {1}{pg}]$
is ind-étale. We claim that
![]() $A_{\infty \infty }$
is a
$A_{\infty \infty }$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay and Witt-perfect algebra. To show that it is Witt-perfect, it suffices to show that the p-adic completion
$(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay and Witt-perfect algebra. To show that it is Witt-perfect, it suffices to show that the p-adic completion
![]() $\widehat {A_{\infty \infty }}$
is integral perfectoid. But this follows from the description appearing in [Reference André2, lemme 2.5.1] and a comment in [Reference Bhatt9, Defn. 2.2] together with an application of [Reference Nakazato and Shimomoto45, Cor. 3.6] (where we should set
$\widehat {A_{\infty \infty }}$
is integral perfectoid. But this follows from the description appearing in [Reference André2, lemme 2.5.1] and a comment in [Reference Bhatt9, Defn. 2.2] together with an application of [Reference Nakazato and Shimomoto45, Cor. 3.6] (where we should set
![]() $g=1$
). In order to show that
$g=1$
). In order to show that
![]() $A_{\infty \infty }$
is
$A_{\infty \infty }$
is
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay, since
$(p)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay, since
![]() $A_{\infty \infty }$
is p-torsion-free, it suffices to show that
$A_{\infty \infty }$
is p-torsion-free, it suffices to show that
![]() $x_2,\ldots ,x_d$
is a
$x_2,\ldots ,x_d$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on
![]() $A_{\infty \infty }/(p)$
in view of Lemma 6.3. By André’s crucial result [Reference André2, théorème 2.5.2],Footnote
12
the induced map
$A_{\infty \infty }/(p)$
in view of Lemma 6.3. By André’s crucial result [Reference André2, théorème 2.5.2],Footnote
12
the induced map
![]() $A_{\infty }/(p) \to A_{\infty \infty }/(p)$
is
$A_{\infty }/(p) \to A_{\infty \infty }/(p)$
is
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost faithfully flat. Hence, the desired claim follows from this fact together with the fact that
$(p)^{\frac {1}{p^{\infty }}}$
-almost faithfully flat. Hence, the desired claim follows from this fact together with the fact that
![]() $p,x_2,\ldots ,x_d$
is a regular sequence on
$p,x_2,\ldots ,x_d$
is a regular sequence on
![]() $A_{\infty }$
.
$A_{\infty }$
.
![]() $(2)$
: By the assertion
$(2)$
: By the assertion
![]() $(1)$
,
$(1)$
,
![]() $(p,g)$
is a
$(p,g)$
is a
![]() $(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on
$(p)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on
![]() $A_{\infty \infty }$
. Next, we study
$A_{\infty \infty }$
. Next, we study
![]() $A_{\infty g}$
and consider
$A_{\infty g}$
and consider
![]() $\widetilde {A_{\infty \infty }}:=\varprojlim _j A^{j\circ }_{\infty \infty }$
attached to
$\widetilde {A_{\infty \infty }}:=\varprojlim _j A^{j\circ }_{\infty \infty }$
attached to
![]() $A_{\infty \infty }$
as defined in (5.5) (see also Theorem 5.16). Then we claim that
$A_{\infty \infty }$
as defined in (5.5) (see also Theorem 5.16). Then we claim that
Since
![]() $A_{\infty g}$
is integrally closed in
$A_{\infty g}$
is integrally closed in
![]() $A_{\infty \infty }[\frac {1}{pg}]=A_{\infty g}[\frac {1}{pg}]$
, it follows from Proposition 7.1 that
$A_{\infty \infty }[\frac {1}{pg}]=A_{\infty g}[\frac {1}{pg}]$
, it follows from Proposition 7.1 that
![]() $A_{\infty g}$
is completely integrally closed in
$A_{\infty g}$
is completely integrally closed in
![]() $A_{\infty \infty }[\frac {1}{pg}]$
. Now by applying Theorem 5.11 to
$A_{\infty \infty }[\frac {1}{pg}]$
. Now by applying Theorem 5.11 to
![]() $A_{\infty \infty }$
, the isomorphism (6.3) follows. By the construction (6.1),
$A_{\infty \infty }$
, the isomorphism (6.3) follows. By the construction (6.1),
![]() $A_{\infty \infty }$
is integrally closed in
$A_{\infty \infty }$
is integrally closed in
![]() $A_{\infty \infty }[\frac {1}{p}]$
. It follows that
$A_{\infty \infty }[\frac {1}{p}]$
. It follows that
![]() $A_{\infty \infty }$
is completely integrally closed in
$A_{\infty \infty }$
is completely integrally closed in
![]() $A_{\infty \infty }[\frac {1}{p}]$
. Then Lemma 3.3 applies to show that the p-adic completion
$A_{\infty \infty }[\frac {1}{p}]$
. Then Lemma 3.3 applies to show that the p-adic completion
![]() $\widehat {A_{\infty \infty }}$
is completely integrally closed in
$\widehat {A_{\infty \infty }}$
is completely integrally closed in
![]() $\widehat {A_{\infty \infty }}[\frac {1}{p}]$
. Now, we can apply Riemann’s extension theorem [Reference André1, théorème 4.2.2] (see Theorem 8.1 for a self-contained proof), together with (6.3), to get that
$\widehat {A_{\infty \infty }}[\frac {1}{p}]$
. Now, we can apply Riemann’s extension theorem [Reference André1, théorème 4.2.2] (see Theorem 8.1 for a self-contained proof), together with (6.3), to get that
 $$ \begin{align*}g^{-\frac{1}{p^{\infty}}}\widehat{A_{\infty \infty}} \cong \varprojlim_j \widehat{A^{j\circ}_{\infty\infty}} \approx \widehat{\varprojlim_j A^{j\circ}_{\infty\infty}} \cong \widehat{A_{\infty g}}, \end{align*} $$
$$ \begin{align*}g^{-\frac{1}{p^{\infty}}}\widehat{A_{\infty \infty}} \cong \varprojlim_j \widehat{A^{j\circ}_{\infty\infty}} \approx \widehat{\varprojlim_j A^{j\circ}_{\infty\infty}} \cong \widehat{A_{\infty g}}, \end{align*} $$
where the middle map is a
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism due to Theorem 5.16. In particular,
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism due to Theorem 5.16. In particular,
![]() $\widehat {A_{\infty \infty }} \to \widehat {A_{\infty g}}$
is a
$\widehat {A_{\infty \infty }} \to \widehat {A_{\infty g}}$
is a
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism.
From the property of
![]() $A_{\infty \infty }$
mentioned in
$A_{\infty \infty }$
mentioned in
![]() $(1)$
, one finds that
$(1)$
, one finds that
![]() $\widehat {A_{\infty g}}$
is an integral
$\widehat {A_{\infty g}}$
is an integral
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost perfectoid and
$(g)^{\frac {1}{p^{\infty }}}$
-almost perfectoid and
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay algebra. By the fact that
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay algebra. By the fact that
![]() $A_{\infty }[\frac {1}{pg}]$
is a normal domain and
$A_{\infty }[\frac {1}{pg}]$
is a normal domain and
![]() $A_{\infty }[\frac {1}{pg}] \to A_{\infty \infty }[\frac {1}{pg}]$
is obtained as a filtered colimit of finite étale
$A_{\infty }[\frac {1}{pg}] \to A_{\infty \infty }[\frac {1}{pg}]$
is obtained as a filtered colimit of finite étale
![]() $A_{\infty }[\frac {1}{pg}]$
-algebras, we see that
$A_{\infty }[\frac {1}{pg}]$
-algebras, we see that
![]() $A_{\infty \infty }[\frac {1}{pg}]$
is a normal ring; the localization at any maximal ideal is an integrally closed domain by Lemma 3.9. Since
$A_{\infty \infty }[\frac {1}{pg}]$
is a normal ring; the localization at any maximal ideal is an integrally closed domain by Lemma 3.9. Since
![]() $A_{\infty g}$
is integrally closed in
$A_{\infty g}$
is integrally closed in
![]() $A_{\infty \infty }[\frac {1}{pg}]$
, it follows that
$A_{\infty \infty }[\frac {1}{pg}]$
, it follows that
![]() $A_{\infty g}$
is also normal.
$A_{\infty g}$
is also normal.
As a corollary, we obtain the following theorem.
Theorem 6.5. Let
![]() $(R,\frak {m})$
be a complete Noetherian local domain of mixed characteristic
$(R,\frak {m})$
be a complete Noetherian local domain of mixed characteristic
![]() $p>0$
with perfect residue field k. Let
$p>0$
with perfect residue field k. Let
![]() $p,x_2,\ldots ,x_d$
be a system of parameters, and let
$p,x_2,\ldots ,x_d$
be a system of parameters, and let
![]() $R^+$
be the absolute integral closure of R. Then there exists an R-algebra T together with a nonzero element
$R^+$
be the absolute integral closure of R. Then there exists an R-algebra T together with a nonzero element
![]() $g \in R$
such that the following hold:
$g \in R$
such that the following hold:
-
1. T admits compatible systems of p-power roots
 $p^{\frac {1}{p^n}}, g^{\frac {1}{p^n}} \in T$
for all
$p^{\frac {1}{p^n}}, g^{\frac {1}{p^n}} \in T$
for all
 $n>0$
.
$n>0$
. -
2. The Frobenius endomorphism
 $Frob:T/(p) \to T/(p)$
is surjective.
$Frob:T/(p) \to T/(p)$
is surjective. -
3. T is a
 $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal domain with respect to
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal domain with respect to
 $p,x_2,\ldots ,x_d$
and
$p,x_2,\ldots ,x_d$
and
 $R \subset T \subset R^+$
.
$R \subset T \subset R^+$
. -
4. The p-adic completion
 $\widehat {T}$
is integral perfectoid.
$\widehat {T}$
is integral perfectoid. -
5.
 $R[\frac {1}{pg}] \to T[\frac {1}{pg}]$
is an ind-étale extension. In other words,
$R[\frac {1}{pg}] \to T[\frac {1}{pg}]$
is an ind-étale extension. In other words,
 $T[\frac {1}{pg}]$
is a filtered colimit of finite étale
$T[\frac {1}{pg}]$
is a filtered colimit of finite étale
 $R[\frac {1}{pg}]$
-algebras contained in
$R[\frac {1}{pg}]$
-algebras contained in
 $T[\frac {1}{pg}]$
.
$T[\frac {1}{pg}]$
.
Proof. In the following, we may assume
![]() $\dim R \ge 2$
without loss of generality. By Cohen’s structure theorem, there is a module-finite extension
$\dim R \ge 2$
without loss of generality. By Cohen’s structure theorem, there is a module-finite extension
As the induced field extension
![]() $\operatorname {Frac}(A) \to \operatorname {Frac}(R)$
is separable, there is an element
$\operatorname {Frac}(A) \to \operatorname {Frac}(R)$
is separable, there is an element
![]() $g \in A \setminus pA$
such that
$g \in A \setminus pA$
such that
![]() $A[\frac {1}{pg}] \to R[\frac {1}{pg}]$
is étale. As in Proposition 6.4, we set
$A[\frac {1}{pg}] \to R[\frac {1}{pg}]$
is étale. As in Proposition 6.4, we set
 $$ \begin{align*}A_{\infty}:=\bigcup_{n>0} W(k)[p^{\frac{1}{p^n}}][[x_2^{\frac{1}{p^n}},\ldots,x_d^{\frac{1}{p^n}}]]. \end{align*} $$
$$ \begin{align*}A_{\infty}:=\bigcup_{n>0} W(k)[p^{\frac{1}{p^n}}][[x_2^{\frac{1}{p^n}},\ldots,x_d^{\frac{1}{p^n}}]]. \end{align*} $$
Now, consider the integral extensions
![]() $A \to A_{\infty } \to A_{\infty \infty } \to A_{\infty g}$
as in Proposition 6.4. Let
$A \to A_{\infty } \to A_{\infty \infty } \to A_{\infty g}$
as in Proposition 6.4. Let
![]() $\frak {n}$
be a maximal ideal of
$\frak {n}$
be a maximal ideal of
![]() $A_{\infty g}$
. Then the localization
$A_{\infty g}$
. Then the localization
![]() $(A_{\infty g})_{\frak {n}}$
is a normal domain that is an integral extension over A and enjoys the same properties as
$(A_{\infty g})_{\frak {n}}$
is a normal domain that is an integral extension over A and enjoys the same properties as
![]() $A_{\infty g}$
. Since
$A_{\infty g}$
. Since
![]() $(p,g)$
forms part of a system of parameters of A and
$(p,g)$
forms part of a system of parameters of A and
![]() $(A_{\infty g})_{\frak {n}}$
is a filtered colimit of module-finite normal A-algebras, it follows that
$(A_{\infty g})_{\frak {n}}$
is a filtered colimit of module-finite normal A-algebras, it follows that
![]() $(p,g)$
is a regular sequence on
$(p,g)$
is a regular sequence on
![]() $(A_{\infty g})_{\frak {n}}$
by Serre’s normality criterion.Footnote
13
By base change, the map
$(A_{\infty g})_{\frak {n}}$
by Serre’s normality criterion.Footnote
13
By base change, the map
 $$ \begin{align} (A_{\infty g})_{\frak{n}}[\frac{1}{pg}] \to R \otimes_A (A_{\infty g})_{\frak{n}}[\frac{1}{pg}] \end{align} $$
$$ \begin{align} (A_{\infty g})_{\frak{n}}[\frac{1}{pg}] \to R \otimes_A (A_{\infty g})_{\frak{n}}[\frac{1}{pg}] \end{align} $$
is finite étale. It follows from [61, Tag 033C] together with the normality of
![]() $(A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
that
$(A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
that
![]() $R \otimes _A (A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
is a normal ring. Letting the notation be as in (6.4), set
$R \otimes _A (A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
is a normal ring. Letting the notation be as in (6.4), set
 $$ \begin{align*}B:=\mbox{the integral closure of}~R~\mbox{in}~R \otimes_A (A_{\infty g})_{\frak{n}}[\frac{1}{pg}]. \end{align*} $$
$$ \begin{align*}B:=\mbox{the integral closure of}~R~\mbox{in}~R \otimes_A (A_{\infty g})_{\frak{n}}[\frac{1}{pg}]. \end{align*} $$
Let K be the field of fractions of
![]() $(A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
, and let
$(A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
, and let
![]() $K \to L$
be the corresponding base change of (6.4). Then the finite étaleness of (6.4) implies that L is the total ring of fractions of
$K \to L$
be the corresponding base change of (6.4). Then the finite étaleness of (6.4) implies that L is the total ring of fractions of
![]() $R \otimes _A (A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
, and L is a finite direct product of fields that are finite separable over K. Since
$R \otimes _A (A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
, and L is a finite direct product of fields that are finite separable over K. Since
![]() $R \otimes _A (A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
is normal, it is integrally closed in L. Then B is identified with the integral closure of R in L. By Lemma 3.9, it follows that B is a normal ring that fits into the commutative diagram:
$R \otimes _A (A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
is normal, it is integrally closed in L. Then B is identified with the integral closure of R in L. By Lemma 3.9, it follows that B is a normal ring that fits into the commutative diagram:

in which every map is injective and integral. Let
![]() $\frak {n}'$
be any maximal ideal of B. Since A is a local domain and
$\frak {n}'$
be any maximal ideal of B. Since A is a local domain and
![]() $A \to B$
is a torsion-free integral extension, one finds that
$A \to B$
is a torsion-free integral extension, one finds that
![]() $A \cap \frak {n}'$
is the unique maximal ideal of A and the induced localization map
$A \cap \frak {n}'$
is the unique maximal ideal of A and the induced localization map
![]() $A \to B_{\frak {n}'}$
is an injective integral extension between normal domains. By setting
$A \to B_{\frak {n}'}$
is an injective integral extension between normal domains. By setting
![]() $A:=(A_{\infty g})_{\frak {n}}$
in the notation of Theorem 5.20 and applying Lemma 6.3, it follows that B is a
$A:=(A_{\infty g})_{\frak {n}}$
in the notation of Theorem 5.20 and applying Lemma 6.3, it follows that B is a
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal ring with respect to
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay normal ring with respect to
![]() $p,x_2,\ldots ,x_d$
and
$p,x_2,\ldots ,x_d$
and
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect. Since these properties are preserved under localization with respect to any maximal ideal, it follows that the normal domain
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Witt-perfect. Since these properties are preserved under localization with respect to any maximal ideal, it follows that the normal domain
![]() $B_{\frak {n}'}$
enjoys the same properties.
$B_{\frak {n}'}$
enjoys the same properties.
To finish the proof, let us put
![]() $C:=B_{\frak {n}'}$
for brevity of notation. Set
$C:=B_{\frak {n}'}$
for brevity of notation. Set
 $$ \begin{align*}T:=\mbox{the integral closure of}~C~\mbox{in}~C[\frac{1}{p}]^{\mathrm{{\acute{e}t}}}, \end{align*} $$
$$ \begin{align*}T:=\mbox{the integral closure of}~C~\mbox{in}~C[\frac{1}{p}]^{\mathrm{{\acute{e}t}}}, \end{align*} $$
where
![]() $C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
is the maximal étale extension of
$C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
is the maximal étale extension of
![]() $C[\frac {1}{p}]$
contained in the absolute integral closure
$C[\frac {1}{p}]$
contained in the absolute integral closure
![]() $C[\frac {1}{p}]^+$
. By using a direct limit argument combined with [61, Tag 033C] and the fact that
$C[\frac {1}{p}]^+$
. By using a direct limit argument combined with [61, Tag 033C] and the fact that
![]() $C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
is a filtered colimit of finite étale
$C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
is a filtered colimit of finite étale
![]() $C[\frac {1}{p}]$
-algebras, we find that the normality of C implies the normality of
$C[\frac {1}{p}]$
-algebras, we find that the normality of C implies the normality of
![]() $C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
. Since T is integrally closed in
$C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
. Since T is integrally closed in
![]() $C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
, T is a normal domain. Thus, T is a Witt-perfect normal domain in view of [Reference Shimomoto58, Lem. 5.1] or [Reference Shimomoto56, Lem. 10.1]. Using this, it can be seen that the p-adic completion
$C[\frac {1}{p}]^{\mathrm {{\acute {e}t}}}$
, T is a normal domain. Thus, T is a Witt-perfect normal domain in view of [Reference Shimomoto58, Lem. 5.1] or [Reference Shimomoto56, Lem. 10.1]. Using this, it can be seen that the p-adic completion
![]() $\widehat {T}$
is integral perfectoid. In other words, the Frobenius map on
$\widehat {T}$
is integral perfectoid. In other words, the Frobenius map on
![]() $\widehat {T}/(p)$
induces an isomorphism:
$\widehat {T}/(p)$
induces an isomorphism:
![]() $\widehat {T}/(p^{\frac {1}{p}}) \cong \widehat {T}/(p)$
. Therefore, it remains to establish that T is
$\widehat {T}/(p^{\frac {1}{p}}) \cong \widehat {T}/(p)$
. Therefore, it remains to establish that T is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay with respect to
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay with respect to
![]() $p,x_2,\ldots ,x_d$
. Let us note that the composite map
$p,x_2,\ldots ,x_d$
. Let us note that the composite map
 $$ \begin{align*}(A_{\infty g})_{\frak{n}}[\frac{1}{pg}] \to C[\frac{1}{pg}] \to T[\frac{1}{pg}] \end{align*} $$
$$ \begin{align*}(A_{\infty g})_{\frak{n}}[\frac{1}{pg}] \to C[\frac{1}{pg}] \to T[\frac{1}{pg}] \end{align*} $$
satisfies that
![]() $T[\frac {1}{pg}]$
is the filtered colimit of finite étale
$T[\frac {1}{pg}]$
is the filtered colimit of finite étale
![]() $(A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
-algebras. As T is integrally closed in its field of fractions, the integral closure of
$(A_{\infty g})_{\frak {n}}[\frac {1}{pg}]$
-algebras. As T is integrally closed in its field of fractions, the integral closure of
![]() $(A_{\infty g})_{\frak {n}}$
in
$(A_{\infty g})_{\frak {n}}$
in
![]() $T[\frac {1}{pg}]$
is the same as T. In the proof of Proposition 6.4, we showed that
$T[\frac {1}{pg}]$
is the same as T. In the proof of Proposition 6.4, we showed that
![]() $\widehat {A}_{\infty \infty } \to \widehat {A}_{\infty g}$
is a
$\widehat {A}_{\infty \infty } \to \widehat {A}_{\infty g}$
is a
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Thus,
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Thus,
![]() $A_{\infty \infty }/(p) \to A_{\infty g}/(p)$
is a
$A_{\infty \infty }/(p) \to A_{\infty g}/(p)$
is a
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Summing up, we conclude from Theorem 5.20 applied to
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Summing up, we conclude from Theorem 5.20 applied to
![]() $A:=(A_{\infty g})_{\frak {n}}$
that
$A:=(A_{\infty g})_{\frak {n}}$
that
![]() $T/(p)$
is the filtered colimit of
$T/(p)$
is the filtered colimit of
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale
$(pg)^{\frac {1}{p^{\infty }}}$
-almost finite étale
![]() $A_{\infty \infty }/(p)$
-algebras. By Lemma 6.3 and Proposition 6.4, T is
$A_{\infty \infty }/(p)$
-algebras. By Lemma 6.3 and Proposition 6.4, T is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost Cohen–Macaulay.
As a corollary, we obtain the following result, which is the strengthened version of the main results in [Reference Heitmann and Ma27]. The proof uses standard results from the theory of local cohomology. For a Noetherian local ring
![]() $(R,\frak {m})$
, let
$(R,\frak {m})$
, let
![]() $H^i_{\frak {m}}(M)$
be the ith local cohomology module of an R-module M with support at the maximal ideal
$H^i_{\frak {m}}(M)$
be the ith local cohomology module of an R-module M with support at the maximal ideal
![]() $\frak {m}$
of R.
$\frak {m}$
of R.
Corollary 6.6. Let the notation and hypotheses be as in Theorem 6.5. Then the local cohomology modules
![]() $H^i_{\frak {m}}(T)$
are
$H^i_{\frak {m}}(T)$
are
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost zero in the range
$(pg)^{\frac {1}{p^{\infty }}}$
-almost zero in the range
![]() $0 \le i \le \dim R-1$
. In particular, the image of the map
$0 \le i \le \dim R-1$
. In particular, the image of the map
![]() $H_{\frak {m}}^i(T) \to H_{\frak {m}}^i(R^+)$
induced by
$H_{\frak {m}}^i(T) \to H_{\frak {m}}^i(R^+)$
induced by
![]() $T \to R^+$
is
$T \to R^+$
is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost zero.
$(pg)^{\frac {1}{p^{\infty }}}$
-almost zero.
Proof. Letting
![]() $p,x_2,\ldots ,x_d$
be a system of parameters of R, if one inspects the structure of the proof of Theorem 6.5 and Theorem 5.20, it follows that
$p,x_2,\ldots ,x_d$
be a system of parameters of R, if one inspects the structure of the proof of Theorem 6.5 and Theorem 5.20, it follows that
![]() $x_2^m,\ldots ,x_d^m$
forms a
$x_2^m,\ldots ,x_d^m$
forms a
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on
$(pg)^{\frac {1}{p^{\infty }}}$
-almost regular sequence on
![]() $T/(p^m)$
for all integers
$T/(p^m)$
for all integers
![]() $m> 0$
. As in the proof of [Reference Heitmann and Ma27, Th. 3.17], the Koszul cohomology modules
$m> 0$
. As in the proof of [Reference Heitmann and Ma27, Th. 3.17], the Koszul cohomology modules
![]() $H^i(p^m,x_2^m,\ldots ,x_d^m;T)$
and hence
$H^i(p^m,x_2^m,\ldots ,x_d^m;T)$
and hence
![]() $H_{\frak {m}}^i(T)$
are
$H_{\frak {m}}^i(T)$
are
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost zero for
$(pg)^{\frac {1}{p^{\infty }}}$
-almost zero for
![]() $i<\dim R$
.
$i<\dim R$
.
It is reasonable to study the following problem, which we credit to Heitmann in the three-dimensional case thanks to his proof of the direct summand conjecture (see [Reference Heitmann25]).
Problem 3. Let
![]() $(R,\frak {m})$
be a complete Noetherian local domain of arbitrary characteristic with its absolute integral closure
$(R,\frak {m})$
be a complete Noetherian local domain of arbitrary characteristic with its absolute integral closure
![]() $R^+$
and the unique maximal ideal
$R^+$
and the unique maximal ideal
![]() $\frak {m}_{R^+}$
. Fix a system of parameters
$\frak {m}_{R^+}$
. Fix a system of parameters
![]() $x_1,\ldots ,x_d$
of R. Then does it hold true that
$x_1,\ldots ,x_d$
of R. Then does it hold true that
for any
![]() $c \in \frak {m}_{R^+}$
and
$c \in \frak {m}_{R^+}$
and
![]() $i=0,\ldots ,d-1$
?
$i=0,\ldots ,d-1$
?
Bhatt gave an even stronger answer to the above problem in mixed characteristic in [Reference Bhatt7] by taking
![]() $x_1=p^n$
, using prismatic cohomology and mod-
$x_1=p^n$
, using prismatic cohomology and mod-
![]() $p^n$
Riemann–Hilbert correspondence. Namely,
$p^n$
Riemann–Hilbert correspondence. Namely,
![]() $p,x_2,\ldots ,x_d$
is a regular sequence on
$p,x_2,\ldots ,x_d$
is a regular sequence on
![]() $R^+$
. In the equal prime characteristic case, Hochster and Huneke already gave a complete answer in [Reference Hochster and Huneke29]. However, almost nothing is known in the equal characteristic zero case. Even in the mixed characteristic case, the above problem is not known to hold true if one starts with an arbitrary system of parameters.
$R^+$
. In the equal prime characteristic case, Hochster and Huneke already gave a complete answer in [Reference Hochster and Huneke29]. However, almost nothing is known in the equal characteristic zero case. Even in the mixed characteristic case, the above problem is not known to hold true if one starts with an arbitrary system of parameters.
Problem 4. Let T be a big Cohen–Macaulay algebra over a Noetherian local domain
![]() $(R,\frak {m})$
.
$(R,\frak {m})$
.
-
• Assume that R has mixed characteristic. Then does T map to an integral perfectoid big Cohen–Macaulay R-algebra?
-
• Assume that R has an arbitrary characteristic. Then does R (or T) map to a coherent big Cohen–Macaulay R-algebra?
For the coherence of absolutely integrally closed domains, see [Reference Patankar47]. Here, we mention a few related results.
Proposition 6.7. Assume that T is a big Cohen–Macaulay algebra over a Noetherian local domain
![]() $(R,\frak {m})$
of any characteristic. Then T maps to an R-algebra B such that the following hold:
$(R,\frak {m})$
of any characteristic. Then T maps to an R-algebra B such that the following hold:
-
1. B is free over T. In particular, B is a big Cohen–Macaulay R-algebra.
-
2. B is absolutely integrally closed. In other words, every nonzero monic polynomial in
 $B[X]$
has a root in B.
$B[X]$
has a root in B.
Proof. Just apply [61, Tag 0DCR].
In relation to Proposition 6.7 and some observations on p-integral closure as discussed in [Reference Cesnavicius and Scholze14], we prove the following fact, which shows that flatness can be destroyed under taking p-integral closure. We refer the reader to [Reference Cesnavicius and Scholze14, 2.1.7] for details on p-integral closure.
Proposition 6.8. Let
![]() $(R,\frak {m})$
be a non-regular local domain of mixed characteristic
$(R,\frak {m})$
be a non-regular local domain of mixed characteristic
![]() $p>0$
. Then there exists a faithfully flat R-algebra T such that
$p>0$
. Then there exists a faithfully flat R-algebra T such that
![]() $p^{\frac {1}{p^n}} \in T$
for
$p^{\frac {1}{p^n}} \in T$
for
![]() $n>0$
and the Frobenius map induces a surjection
$n>0$
and the Frobenius map induces a surjection
![]() $T/(p^{\frac {1}{p}}) \to T/(p)$
. Moreover, let T be any R-algebra with the aforementioned properties, and let
$T/(p^{\frac {1}{p}}) \to T/(p)$
. Moreover, let T be any R-algebra with the aforementioned properties, and let
![]() $\widetilde {T}$
be the p-integral closure of T in
$\widetilde {T}$
be the p-integral closure of T in
![]() $T[\frac {1}{p}]$
. Then the p-adic completion of
$T[\frac {1}{p}]$
. Then the p-adic completion of
![]() $\widetilde {T}$
is integral perfectoid, but
$\widetilde {T}$
is integral perfectoid, but
![]() $\widetilde {T}$
is never flat over R.
$\widetilde {T}$
is never flat over R.
Proof. The first assertion is due to Proposition 6.7. It follows from [Reference Cesnavicius and Scholze14, Prop. 2.1.8] that the p-adic completion
![]() $\widehat {\widetilde {T}}$
is integral perfectoid. Assume that
$\widehat {\widetilde {T}}$
is integral perfectoid. Assume that
![]() $\widetilde {T}$
is flat over R. Since
$\widetilde {T}$
is flat over R. Since
![]() $T \to \widetilde {T}$
is an integral extension, it follows that
$T \to \widetilde {T}$
is an integral extension, it follows that
![]() $\widetilde {T}$
is faithfully flat over R. Moreover,
$\widetilde {T}$
is faithfully flat over R. Moreover,
![]() $\widehat {\widetilde {T}}$
is faithfully flat over R by [Reference Yekutieli63, Th. 0.1]. But the main result of [Reference Bhatt, Iyengar and Ma10] forces R to be regular, which contradicts the hypothesis that R is not regular.
$\widehat {\widetilde {T}}$
is faithfully flat over R by [Reference Yekutieli63, Th. 0.1]. But the main result of [Reference Bhatt, Iyengar and Ma10] forces R to be regular, which contradicts the hypothesis that R is not regular.
Theorem 6.9 (Gabber–Ramero)
Let
![]() $(R,\frak {m})$
be a complete local domain of mixed characteristic. Then any integral perfectoid big Cohen–Macaulay R-algebra B admits an R-algebra map
$(R,\frak {m})$
be a complete local domain of mixed characteristic. Then any integral perfectoid big Cohen–Macaulay R-algebra B admits an R-algebra map
![]() $B \to C$
such that C is an integral perfectoid big Cohen–Macaulay R-algebra and C is an absolutely integrally closed quasi-local domain.
$B \to C$
such that C is an integral perfectoid big Cohen–Macaulay R-algebra and C is an absolutely integrally closed quasi-local domain.
Proof. See [Reference Gabber and Ramero21, Th. 17.5.96].
Problem 5. Let
![]() $(R,\frak {m})$
be a complete Noetherian local domain of mixed characteristic. Then can one construct a big Cohen–Macaulay R-algebra T such that T has bounded p-power roots of p or equivalently, the radical ideal
$(R,\frak {m})$
be a complete Noetherian local domain of mixed characteristic. Then can one construct a big Cohen–Macaulay R-algebra T such that T has bounded p-power roots of p or equivalently, the radical ideal
![]() $\sqrt {pT}$
is finitely generated?
$\sqrt {pT}$
is finitely generated?
So far, big Cohen–Macaulay algebras constructed using perfectoids necessarily admit p-power roots of p and we do not know if the construction as stated in Problem 5 is possible.
Problem 6. Let the notation be the same as that of Theorem 5.16. Then under what condition is it true that
![]() $ \widehat {\varprojlim _{j>0} A^{j\circ }} \hookrightarrow \varprojlim _{j>0} \widehat {A^{j\circ }}$
is an isomorphism?
$ \widehat {\varprojlim _{j>0} A^{j\circ }} \hookrightarrow \varprojlim _{j>0} \widehat {A^{j\circ }}$
is an isomorphism?
This is connected with the Mittag-Leffler condition (see [Reference Gabber and Ramero21, Cor. 8.2.16] for a relevant result). The article [Reference Gabber and Ramero21] also introduces and discusses the almost variant of the Mittag-Leffler condition. Bhatt and Scholze introduced the “perfectoidization functor” over semiperfectoid rings. While our present article is independent from [Reference Bhatt and Scholze11], we are left to investigate the relationship between
![]() $\widehat {T}$
from Theorem 6.5 and
$\widehat {T}$
from Theorem 6.5 and
![]() $(A_{\infty g} \otimes _A R)_{\mathrm {{perfd}}}$
.
$(A_{\infty g} \otimes _A R)_{\mathrm {{perfd}}}$
.
6.2 A construction of big Cohen–Macaulay modules
We demonstrate a method of constructing a big Cohen–Macaulay module by using the R-algebra T from Theorem 6.5.
Corollary 6.10. Let the notation be as in Theorem 6.5. Set
![]() $M:=(pg)^{\frac {1}{p^{\infty }}}T$
. Then M is an ideal of T that is
$M:=(pg)^{\frac {1}{p^{\infty }}}T$
. Then M is an ideal of T that is
![]() $(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphic to T, and M is a big Cohen–Macaulay R-module. In other words,
$(pg)^{\frac {1}{p^{\infty }}}$
-almost isomorphic to T, and M is a big Cohen–Macaulay R-module. In other words,
![]() $H^i_{\frak {m}}(M)=0$
for all
$H^i_{\frak {m}}(M)=0$
for all
![]() $0 \le i \le \dim R-1$
.
$0 \le i \le \dim R-1$
.
Proof. Notice that T is
![]() $pg$
-torsion-free and there is an isomorphism as T-modules:
$pg$
-torsion-free and there is an isomorphism as T-modules:
![]() $T \cong (pg)^{\frac {1}{p^n}}T$
. Consider the commutative diagram:
$T \cong (pg)^{\frac {1}{p^n}}T$
. Consider the commutative diagram:

where the horizontal arrows in the bottom are natural injections, and the vertical arrows are bijections. Fix any
![]() $i<\dim R$
. Applying the local cohomology to this commutative diagram, the bottom horizontal sequence becomes
$i<\dim R$
. Applying the local cohomology to this commutative diagram, the bottom horizontal sequence becomes
 $$ \begin{align} \varinjlim_{n>0} H_{\frak{m}}^i((pg)^{\frac{1}{p^n}}T) \cong H_{\frak{m}}^i(\varinjlim_{n>0}(pg)^{\frac{1}{p^n}}T) \cong H_{\frak{m}}^i(M), \end{align} $$
$$ \begin{align} \varinjlim_{n>0} H_{\frak{m}}^i((pg)^{\frac{1}{p^n}}T) \cong H_{\frak{m}}^i(\varinjlim_{n>0}(pg)^{\frac{1}{p^n}}T) \cong H_{\frak{m}}^i(M), \end{align} $$
where the first isomorphism uses the commutativity of cohomological functor with direct limit. The horizontal upper sequence becomes
 $$ \begin{align} \varinjlim_{n} \Big\{H_{\frak{m}}^i(T) \xrightarrow{\times(pg)^{1-\frac{1}{p}}} H_{\frak{m}}^i(T) \xrightarrow{\times (pg)^{\frac{1}{p}-\frac{1}{p^2}}} H_{\frak{m}}^i(T) \to \cdots \Big\} \cong 0, \end{align} $$
$$ \begin{align} \varinjlim_{n} \Big\{H_{\frak{m}}^i(T) \xrightarrow{\times(pg)^{1-\frac{1}{p}}} H_{\frak{m}}^i(T) \xrightarrow{\times (pg)^{\frac{1}{p}-\frac{1}{p^2}}} H_{\frak{m}}^i(T) \to \cdots \Big\} \cong 0, \end{align} $$
because the local cohomology modules
![]() $H_{\frak {m}}^i(T)$
are annihilated by
$H_{\frak {m}}^i(T)$
are annihilated by
![]() $(pg)^{\frac {1}{p^n}}$
for any
$(pg)^{\frac {1}{p^n}}$
for any
![]() $n>0$
and
$n>0$
and
![]() $i<\dim R$
. As (6.5) and (6.6) yield the isomorphic modules, we have the desired vanishing cohomology.
$i<\dim R$
. As (6.5) and (6.6) yield the isomorphic modules, we have the desired vanishing cohomology.
Since R is a Noetherian local domain, there is a discrete valuation
![]() $v:R \to \mathbb {Z}_{\ge 0} \cup \{\infty \}$
with center on the maximal ideal. Then one extends v as a
$v:R \to \mathbb {Z}_{\ge 0} \cup \{\infty \}$
with center on the maximal ideal. Then one extends v as a
![]() $\mathbb {Q}$
-valued valuation on T. One can use this valuation to deduce that
$\mathbb {Q}$
-valued valuation on T. One can use this valuation to deduce that
![]() $M \ne \frak {m} M$
and the details are left as an exercise (see also [Reference Asgharzadeh and Shimomoto5, Lem. 3.15]).
$M \ne \frak {m} M$
and the details are left as an exercise (see also [Reference Asgharzadeh and Shimomoto5, Lem. 3.15]).
7 Appendix A: Almost integrality under finiteness conditions
In this appendix, our aim is to give a proof to the following result (see Proposition 7.1). As in Corollary 5.9, for a topological space X, we denote by
![]() $[X]$
the maximal separated quotient of X, thus defining the natural epimorphism
$[X]$
the maximal separated quotient of X, thus defining the natural epimorphism
![]() $X \to [X]$
.
$X \to [X]$
.
Proposition 7.1. Let
![]() $A_0$
be a ring that is integral over a Noetherian ring, and let
$A_0$
be a ring that is integral over a Noetherian ring, and let
![]() $t\in A_0$
be a regular element. Then an element
$t\in A_0$
be a regular element. Then an element
![]() $a\in A_0[\frac {1}{t}]$
is integral over
$a\in A_0[\frac {1}{t}]$
is integral over
![]() $A_0$
if and only if it is almost integral over
$A_0$
if and only if it is almost integral over
![]() $A_0$
. More precisely, for the Tate ring A associated with
$A_0$
. More precisely, for the Tate ring A associated with
![]() $(A_0, (t))$
, we have
$(A_0, (t))$
, we have
The idea of our proof is to reduce the assertion to the situation of Corollary 5.9, using Zariskization. Let us recall its definition below (see also [Reference Fujiwara and Kato19, Chap. 0, 7.3(b)] or [Reference Tanaka60, Defn. 3.1]).
Definition 7.2. Let A be a ring with an ideal
![]() $I\subset A$
. Then we denote by
$I\subset A$
. Then we denote by
![]() $A^{Zar}_I$
the localization
$A^{Zar}_I$
the localization
![]() $(1+I)^{-1}A$
, and call it the I-adic Zariskization of A.
$(1+I)^{-1}A$
, and call it the I-adic Zariskization of A.
We will utilize the following properties of Zariskization.
Lemma 7.3. Let
![]() $A\subset B$
be an integral ring extension, and let
$A\subset B$
be an integral ring extension, and let
![]() $I\subset A$
be an ideal. Then the following assertions hold:
$I\subset A$
be an ideal. Then the following assertions hold:
-
1. The induced ring map
 $A^{Zar}_I\to B^{Zar}_{IB}$
is also integral.
$A^{Zar}_I\to B^{Zar}_{IB}$
is also integral. -
2. Let
 $\{A_{\lambda }\}_{\lambda \in \Lambda }$
be the filtered system of all module-finite A-subalgebras of B. Then we have a canonical isomorphism of rings
$\{A_{\lambda }\}_{\lambda \in \Lambda }$
be the filtered system of all module-finite A-subalgebras of B. Then we have a canonical isomorphism of rings
 $\varinjlim _{\lambda } (A_{\lambda })^{Zar}_{IA_{\lambda }}\xrightarrow {\cong }B^{Zar}_{IB}$
.
$\varinjlim _{\lambda } (A_{\lambda })^{Zar}_{IA_{\lambda }}\xrightarrow {\cong }B^{Zar}_{IB}$
.
Proof.
![]() $(1)$
: Set
$(1)$
: Set
![]() $B'=B\otimes _{A}A^{Zar}_I$
. Then the map
$B'=B\otimes _{A}A^{Zar}_I$
. Then the map
![]() $A^{Zar}_I\to B^{Zar}_{IB}$
is given as the composite of the integral map
$A^{Zar}_I\to B^{Zar}_{IB}$
is given as the composite of the integral map
![]() $A^{Zar}_I\to B'$
and the canonical B-algebra map
$A^{Zar}_I\to B'$
and the canonical B-algebra map
![]() $B'\to B^{Zar}_{IB}$
. Moreover, since
$B'\to B^{Zar}_{IB}$
. Moreover, since
![]() $B'$
is
$B'$
is
![]() $IB'$
-adically Zariskian, we have the B-algebra map
$IB'$
-adically Zariskian, we have the B-algebra map
![]() $B^{Zar}_{IB}\to B'$
. Since the composite
$B^{Zar}_{IB}\to B'$
. Since the composite
![]() $B^{Zar}_{IB}\to B'\to B^{Zar}_{IB}$
is the identity map by the universal property, the map
$B^{Zar}_{IB}\to B'\to B^{Zar}_{IB}$
is the identity map by the universal property, the map
![]() $B'\to B^{Zar}_{IB}$
is surjective. Hence the assertion follows.
$B'\to B^{Zar}_{IB}$
is surjective. Hence the assertion follows.
![]() $(2)$
: Since B is integral over A, we have
$(2)$
: Since B is integral over A, we have
![]() $\varinjlim _{\lambda } A_{\lambda }=B$
. For each
$\varinjlim _{\lambda } A_{\lambda }=B$
. For each
![]() $\lambda \in \Lambda $
, the map
$\lambda \in \Lambda $
, the map
![]() $A_{\lambda }\hookrightarrow B$
induces the
$A_{\lambda }\hookrightarrow B$
induces the
![]() $A_{\lambda }$
-algebra map
$A_{\lambda }$
-algebra map
![]() $\varphi _{\lambda }: (A_{\lambda })^{Zar}_{IA_{\lambda }}\to B^{Zar}_{IB}$
. Hence, we have the B-algebra map
$\varphi _{\lambda }: (A_{\lambda })^{Zar}_{IA_{\lambda }}\to B^{Zar}_{IB}$
. Hence, we have the B-algebra map
![]() $\varphi : \varinjlim _{\lambda }(A_{\lambda })^{Zar}_{IA_{\lambda }}\to B^{Zar}_{IB}$
. Now, for any
$\varphi : \varinjlim _{\lambda }(A_{\lambda })^{Zar}_{IA_{\lambda }}\to B^{Zar}_{IB}$
. Now, for any
![]() $x\in IB$
, there exists some
$x\in IB$
, there exists some
![]() $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
![]() $1+x\in 1+IA_{\lambda }$
. Hence
$1+x\in 1+IA_{\lambda }$
. Hence
![]() $\varphi $
is injective. Set
$\varphi $
is injective. Set
![]() $C:=\varinjlim _{\lambda }(A_{\lambda })^{Zar}_{IA_{\lambda }}$
. Since
$C:=\varinjlim _{\lambda }(A_{\lambda })^{Zar}_{IA_{\lambda }}$
. Since
![]() $A^{Zar}_I\to C$
is integral by the assertion (1), C is
$A^{Zar}_I\to C$
is integral by the assertion (1), C is
![]() $IC$
-adically Zariskian. Hence, we obtain the B-algebra map
$IC$
-adically Zariskian. Hence, we obtain the B-algebra map
![]() $\psi : B^{Zar}_{IB}\to C^{Zar}_{IC}$
, and the composite
$\psi : B^{Zar}_{IB}\to C^{Zar}_{IC}$
, and the composite
![]() $\varphi \circ \psi $
is the identity map by the universal property. Therefore
$\varphi \circ \psi $
is the identity map by the universal property. Therefore
![]() $\varphi $
is surjective. Thus the assertion follows.
$\varphi $
is surjective. Thus the assertion follows.
Corollary 7.4. Let
![]() $A_0$
be a ring with a regular element
$A_0$
be a ring with a regular element
![]() $t \in A_0$
. Put
$t \in A_0$
. Put
![]() $A:=A_0[\frac {1}{t}]$
and
$A:=A_0[\frac {1}{t}]$
and
![]() $A':=({A_0})^{Zar}_{(t)}[\frac {1}{t}]$
. Then the inclusion
$A':=({A_0})^{Zar}_{(t)}[\frac {1}{t}]$
. Then the inclusion
![]() $A_0\hookrightarrow (A_0)^+_{A}$
induces an isomorphism
$A_0\hookrightarrow (A_0)^+_{A}$
induces an isomorphism
![]() $(({A_0})^{Zar}_{(t)})^+_{A'}\xrightarrow {\cong }((A_0)^+_A)^{Zar}_{(t)}$
.
$(({A_0})^{Zar}_{(t)})^+_{A'}\xrightarrow {\cong }((A_0)^+_A)^{Zar}_{(t)}$
.
Proof. Since integrality of a ring extension is preserved under localization, it suffices to show that
![]() $((A_0)^+_A)^{Zar}_{(t)}\cong (A_0)^+_A\otimes _{A_0}(A_0)^{Zar}_{(t)}$
. First, we have an isomorphism
$((A_0)^+_A)^{Zar}_{(t)}\cong (A_0)^+_A\otimes _{A_0}(A_0)^{Zar}_{(t)}$
. First, we have an isomorphism
![]() $\varinjlim _{\lambda }(A_{\lambda })^{Zar}_{(t)}\xrightarrow {\cong } ((A_0)^+_A)^{Zar}_{(t)}$
by Lemma 7.3(2). Moreover, for each
$\varinjlim _{\lambda }(A_{\lambda })^{Zar}_{(t)}\xrightarrow {\cong } ((A_0)^+_A)^{Zar}_{(t)}$
by Lemma 7.3(2). Moreover, for each
![]() $\lambda \in \Lambda $
, there exists some
$\lambda \in \Lambda $
, there exists some
![]() $m>0$
for which
$m>0$
for which
![]() $t^mA_{\lambda }\subset A_0$
. Then, since
$t^mA_{\lambda }\subset A_0$
. Then, since
![]() $1+t^{m+1}A_{\lambda }\subset 1+tA_0$
, we have
$1+t^{m+1}A_{\lambda }\subset 1+tA_0$
, we have
![]() $(A_{\lambda })^{Zar}_{(t)} \cong (A_{\lambda })^{Zar}_{(t^{m+1})}\cong A_{\lambda }\otimes _{A_0}(A_0)^{Zar}_{(t)}$
. Thus the assertion follows.
$(A_{\lambda })^{Zar}_{(t)} \cong (A_{\lambda })^{Zar}_{(t^{m+1})}\cong A_{\lambda }\otimes _{A_0}(A_0)^{Zar}_{(t)}$
. Thus the assertion follows.
Now, we can complete the proof of Proposition 7.1.
Proof of Proposition 7.1
Set
![]() $X=\operatorname {Spa}(A, (A_0)^+_A)$
. Since we know that
$X=\operatorname {Spa}(A, (A_0)^+_A)$
. Since we know that
it suffices to show the reverse inclusion. Pick
![]() $c\in A$
such that
$c\in A$
such that
![]() $|c|_x\leq 1$
for any
$|c|_x\leq 1$
for any
![]() $x\in [X]$
. By assumption, there exists a Noetherian subring
$x\in [X]$
. By assumption, there exists a Noetherian subring
![]() $R\subset A_0$
such that
$R\subset A_0$
such that
![]() $t\in R$
and the filtered system
$t\in R$
and the filtered system
![]() $\{R_{\lambda }\}_{\lambda \in \Lambda }$
of all module-finite R-subalgebras in
$\{R_{\lambda }\}_{\lambda \in \Lambda }$
of all module-finite R-subalgebras in
![]() $A_0$
satisfies
$A_0$
satisfies
![]() $A_0=\varinjlim _{\lambda }R_{\lambda }$
. Then by Lemma 7.3,
$A_0=\varinjlim _{\lambda }R_{\lambda }$
. Then by Lemma 7.3,
![]() $A^{\prime }_0:=\varinjlim _{\lambda } (R_{\lambda })^{Zar}_{(t)}$
is integral over a Noetherian ring
$A^{\prime }_0:=\varinjlim _{\lambda } (R_{\lambda })^{Zar}_{(t)}$
is integral over a Noetherian ring
![]() $R^{Zar}_{(t)}$
. Let
$R^{Zar}_{(t)}$
. Let
![]() $A'$
be the Tate ring associated with
$A'$
be the Tate ring associated with
![]() $(A^{\prime }_0, (t))$
, and
$(A^{\prime }_0, (t))$
, and
![]() $X'=\operatorname {Spa}(A', (A^{\prime }_0)^+_{A'})$
. Then Corollary 5.9 implies that
$X'=\operatorname {Spa}(A', (A^{\prime }_0)^+_{A'})$
. Then Corollary 5.9 implies that
Moreover, for the continuous ring map
![]() $\psi : A\to A'$
, we have
$\psi : A\to A'$
, we have
![]() $|\psi (c)|_{x'}\leq 1$
for any
$|\psi (c)|_{x'}\leq 1$
for any
![]() $x'\in X'$
by assumption. Thus, we find that
$x'\in X'$
by assumption. Thus, we find that
![]() $\psi (c)\in (A^{\prime }_0)^+_{A'}$
. On the other hand,
$\psi (c)\in (A^{\prime }_0)^+_{A'}$
. On the other hand,
![]() $A^{\prime }_0\cong (A_0)^{Zar}_{(t)}$
by Lemma 7.3 and hence we have
$A^{\prime }_0\cong (A_0)^{Zar}_{(t)}$
by Lemma 7.3 and hence we have
by Lemma 7.4. Since the map
![]() $(A_0)^+_A\to ((A_0)^+_A)^{Zar}_{(t)}$
becomes an isomorphism after t-adic completion, one can deduce from Beauville–Laszlo’s lemma (Lemma 3.1) that the diagram of ring maps
$(A_0)^+_A\to ((A_0)^+_A)^{Zar}_{(t)}$
becomes an isomorphism after t-adic completion, one can deduce from Beauville–Laszlo’s lemma (Lemma 3.1) that the diagram of ring maps

is Cartesian. Thus, we obtain
![]() $c\in (A_0)^+_A$
, as wanted.
$c\in (A_0)^+_A$
, as wanted.
8 Appendix B: Almost vanishing of derived limits
We give a self-contained account of the proof of the Riemann’s extension theorem, as proved by André and its consequence on the almost vanishing of the derived limits of a certain tower of perfectoid algebras. This appendix is also meant to help the reader understand André’s articles [Reference André1] and [Reference André2]. See [Reference André1, théorème 4.2.2] and [Reference André1, Prop. 4.4.1] for the following results, respectively.
Theorem 8.1 (Riemann’s extension theorem for perfectoid algebras)
Fix a perfectoid K-algebra
![]() $\mathcal {A}$
, where K is a perfectoid field with a nonzero element
$\mathcal {A}$
, where K is a perfectoid field with a nonzero element
![]() $\varpi \in K^{\circ }$
admitting all p-power roots, and let
$\varpi \in K^{\circ }$
admitting all p-power roots, and let
![]() $g \in \mathcal {A}^{\circ }$
be an element that admits a compatible system of p-power roots
$g \in \mathcal {A}^{\circ }$
be an element that admits a compatible system of p-power roots
![]() $\{g^{\frac {1}{p^m}}\}_{m>0}$
, such that g is a
$\{g^{\frac {1}{p^m}}\}_{m>0}$
, such that g is a
![]() $(\varpi )^{\frac {1}{p^{\infty }}}$
-almost regular element of
$(\varpi )^{\frac {1}{p^{\infty }}}$
-almost regular element of
![]() $\mathcal {A}^{\circ }/(\varpi ^r)$
for any fixed
$\mathcal {A}^{\circ }/(\varpi ^r)$
for any fixed
![]() $r \in \mathbb {N}[\frac {1}{p}]$
. Then there is an isomorphism:
$r \in \mathbb {N}[\frac {1}{p}]$
. Then there is an isomorphism:
 $$ \begin{align*}\varprojlim_{j>0} \mathcal{A} \big\{\frac{\varpi^j}{g}\big\}^{\circ} \cong g^{-\frac{1}{p^{\infty}}} \mathcal{A}^{\circ}. \end{align*} $$
$$ \begin{align*}\varprojlim_{j>0} \mathcal{A} \big\{\frac{\varpi^j}{g}\big\}^{\circ} \cong g^{-\frac{1}{p^{\infty}}} \mathcal{A}^{\circ}. \end{align*} $$
Proof. Throughout the proof, we fix
![]() $r \in \mathbb {N}[\frac {1}{p}]$
and for a given
$r \in \mathbb {N}[\frac {1}{p}]$
and for a given
![]() $j \in \mathbb {N}$
, we set
$j \in \mathbb {N}$
, we set
 $$ \begin{align*}A^j_0:=\mathcal{A}^{\circ}/(\varpi^r)\big[\big(\frac{\varpi^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]. \end{align*} $$
$$ \begin{align*}A^j_0:=\mathcal{A}^{\circ}/(\varpi^r)\big[\big(\frac{\varpi^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]. \end{align*} $$
Then the natural ring map
![]() $\eta _j:A^{j+1}_0 \to A^{j}_0$
is defined by
$\eta _j:A^{j+1}_0 \to A^{j}_0$
is defined by
![]() $\frac {\varpi ^{j+1}}{g} \mapsto \varpi \cdot \frac {\varpi ^j}{g}$
and hence
$\frac {\varpi ^{j+1}}{g} \mapsto \varpi \cdot \frac {\varpi ^j}{g}$
and hence
![]() $\{A^j_0\}_{j \in \mathbb {N}}$
forms an inverse system.Footnote
14
Now, we claim that the natural map
$\{A^j_0\}_{j \in \mathbb {N}}$
forms an inverse system.Footnote
14
Now, we claim that the natural map
 $$ \begin{align} f:\mathcal{A}^{\circ}/(\varpi^r) \to \varprojlim_j A^j_0 \end{align} $$
$$ \begin{align} f:\mathcal{A}^{\circ}/(\varpi^r) \to \varprojlim_j A^j_0 \end{align} $$
is a
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. First, we show that f is
$(g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. First, we show that f is
![]() $(g)^{\frac {1}{\infty }}$
-almost injective. But we remark that the localization map
$(g)^{\frac {1}{\infty }}$
-almost injective. But we remark that the localization map
![]() $\mathcal {A}^{\circ }/(\varpi ^r) \to \mathcal {A}^{\circ }/(\varpi )^r[\frac {1}{g}]$
factors as
$\mathcal {A}^{\circ }/(\varpi ^r) \to \mathcal {A}^{\circ }/(\varpi )^r[\frac {1}{g}]$
factors as
![]() $\mathcal {A}^{\circ }/(\varpi ^r) \to A^j_0 \to \mathcal {A}^{\circ }/(\varpi )^r[\frac {1}{g}]$
which is
$\mathcal {A}^{\circ }/(\varpi ^r) \to A^j_0 \to \mathcal {A}^{\circ }/(\varpi )^r[\frac {1}{g}]$
which is
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost injective by our hypothesis. So it suffices to treat the cokernel of f. Consider the commutative diagram:
$(g)^{\frac {1}{p^{\infty }}}$
-almost injective by our hypothesis. So it suffices to treat the cokernel of f. Consider the commutative diagram:

For any fixed
![]() $m>0$
, we must show that
$m>0$
, we must show that
 $$ \begin{align} \eta_j\circ \cdots \circ \eta_{j+c-1}\Big(g^{\frac{1}{p^m}} \cdot \Big(\frac{\varpi^{j+c}}{g}\Big)^{\frac{i}{p^n}}\Big) \in \operatorname{Im}(f_j)~\mbox{in}~A^j_0~\mbox{for}~\forall c\ge p^mr~\mbox{and}~i,n>0. \end{align} $$
$$ \begin{align} \eta_j\circ \cdots \circ \eta_{j+c-1}\Big(g^{\frac{1}{p^m}} \cdot \Big(\frac{\varpi^{j+c}}{g}\Big)^{\frac{i}{p^n}}\Big) \in \operatorname{Im}(f_j)~\mbox{in}~A^j_0~\mbox{for}~\forall c\ge p^mr~\mbox{and}~i,n>0. \end{align} $$
First, assume that
![]() $p^n \le ip^m$
. Then as
$p^n \le ip^m$
. Then as
![]() $c\ge p^mr$
, we have
$c\ge p^mr$
, we have
![]() $\varpi ^r \mid \varpi ^{\frac {c}{p^m}}$
. Hence
$\varpi ^r \mid \varpi ^{\frac {c}{p^m}}$
. Hence
![]() $\varpi ^r \mid \varpi ^{\frac {ci}{p^n}}$
. This shows that
$\varpi ^r \mid \varpi ^{\frac {ci}{p^n}}$
. This shows that
 $$ \begin{align*}\Big(\frac{\varpi^{j+c}}{g}\Big)^{\frac{i}{p^n}}=\varpi^{\frac{ci}{p^n}} \cdot \Big(\frac{\varpi^{j}}{g}\Big)^{\frac{i}{p^n}}=0, \end{align*} $$
$$ \begin{align*}\Big(\frac{\varpi^{j+c}}{g}\Big)^{\frac{i}{p^n}}=\varpi^{\frac{ci}{p^n}} \cdot \Big(\frac{\varpi^{j}}{g}\Big)^{\frac{i}{p^n}}=0, \end{align*} $$
which gives (8.2) under the assumption
![]() $p^n \le ip^m$
. Second, assume that
$p^n \le ip^m$
. Second, assume that
![]() $p^n> ip^m$
. In this case, we get the following:
$p^n> ip^m$
. In this case, we get the following:
 $$ \begin{align*}g^{\frac{1}{p^m}} \cdot \Big(\frac{\varpi^{j+c}}{g}\Big)^{\frac{i}{p^n}}=g^{\frac{1}{p^m}-\frac{i}{p^n}} \cdot \varpi^{\frac{ji+ci}{p^n}} \in \operatorname{Im}(f_r), \end{align*} $$
$$ \begin{align*}g^{\frac{1}{p^m}} \cdot \Big(\frac{\varpi^{j+c}}{g}\Big)^{\frac{i}{p^n}}=g^{\frac{1}{p^m}-\frac{i}{p^n}} \cdot \varpi^{\frac{ji+ci}{p^n}} \in \operatorname{Im}(f_r), \end{align*} $$
which gives (8.2) under the assumption
![]() $p^n> ip^m$
. So we proved that for any given
$p^n> ip^m$
. So we proved that for any given
![]() $m>0$
, if we choose c such that
$m>0$
, if we choose c such that
![]() $c \ge p^mr$
, then it follows that
$c \ge p^mr$
, then it follows that
So combining (8.1) and [Reference Scholze52, Lem. 6.4] together, we find that
 $$ \begin{align*}\mathcal{A}^{\circ}/(\varpi^r) \to \varprojlim_{j>0} \Big(\mathcal{A} \big\{\frac{\varpi^j}{g}\big\}^{\circ}/(\varpi^r)\Big) \end{align*} $$
$$ \begin{align*}\mathcal{A}^{\circ}/(\varpi^r) \to \varprojlim_{j>0} \Big(\mathcal{A} \big\{\frac{\varpi^j}{g}\big\}^{\circ}/(\varpi^r)\Big) \end{align*} $$
is a
![]() $(\varpi g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. After taking the inverse limits,
$(\varpi g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. After taking the inverse limits,
 $$ \begin{align*}\mathcal{A}^{\circ} \to \varprojlim_{j>0} \mathcal{A} \big\{\frac{\varpi^j}{g}\big\}^{\circ} \end{align*} $$
$$ \begin{align*}\mathcal{A}^{\circ} \to \varprojlim_{j>0} \mathcal{A} \big\{\frac{\varpi^j}{g}\big\}^{\circ} \end{align*} $$
is a
![]() $(\varpi g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Applying the functor of almost elements
$(\varpi g)^{\frac {1}{p^{\infty }}}$
-almost isomorphism. Applying the functor of almost elements
![]() $(\varpi g)^{-\frac {1}{p^{\infty }}}(~)$
on both sides, we obtain the desired isomorphism.
$(\varpi g)^{-\frac {1}{p^{\infty }}}(~)$
on both sides, we obtain the desired isomorphism.
Corollary 8.2 (Almost vanishing of
 $\varprojlim ^1$
)
$\varprojlim ^1$
)
Let the notation and hypotheses be the same as in Theorem 8.1 and fix
![]() $r \in \mathbb {N}[\frac {1}{p}]$
. Set
$r \in \mathbb {N}[\frac {1}{p}]$
. Set
 $$ \begin{align*}A^j_0:=\mathcal{A}^{\circ}/(\varpi^r)\big[\big(\frac{\varpi^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]~\mbox{for}~j \in \mathbb{N}. \end{align*} $$
$$ \begin{align*}A^j_0:=\mathcal{A}^{\circ}/(\varpi^r)\big[\big(\frac{\varpi^j}{g}\big)^{\frac{1}{p^{\infty}}}\big]~\mbox{for}~j \in \mathbb{N}. \end{align*} $$
Then the inverse system
![]() $\{A^j_0\}_{j \in \mathbb {N}}$
gives a
$\{A^j_0\}_{j \in \mathbb {N}}$
gives a
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost vanishing
$(g)^{\frac {1}{p^{\infty }}}$
-almost vanishing
 $$ \begin{align*}{\varprojlim_{j \in \mathbb{N}}}^1 A^j_0 \approx 0. \end{align*} $$
$$ \begin{align*}{\varprojlim_{j \in \mathbb{N}}}^1 A^j_0 \approx 0. \end{align*} $$
Proof. Without loss of generality, we may assume that g is a regular element of
![]() $\mathcal {A}^{\circ }/(\varpi ^r)$
for any
$\mathcal {A}^{\circ }/(\varpi ^r)$
for any
![]() $r \in \mathbb {N}$
. Keep the notation as in Theorem 8.1. Then we have a commutative diagram:
$r \in \mathbb {N}$
. Keep the notation as in Theorem 8.1. Then we have a commutative diagram:

where each horizontal sequence is exact.
Fix an integer
![]() $m>0$
. Let us put
$m>0$
. Let us put
![]() $N_j:=\operatorname {Coker}(f_j)$
. Then choose
$N_j:=\operatorname {Coker}(f_j)$
. Then choose
![]() $c(m) \in \mathbb {N}$
according to (8.3) such that the image of the map
$c(m) \in \mathbb {N}$
according to (8.3) such that the image of the map
![]() $N_{j+c(m)} \to N_j$
is annihilated by
$N_{j+c(m)} \to N_j$
is annihilated by
![]() $g^{\frac {1}{p^m}}$
. Put
$g^{\frac {1}{p^m}}$
. Put
![]() $k(m,n):=1+n \cdot c(m)$
. Then for any fixed
$k(m,n):=1+n \cdot c(m)$
. Then for any fixed
![]() $m>0$
,
$m>0$
,
![]() $\{A_0^{k(m,n)}\}_{n \in \mathbb {N}}$
forms a cofinal subsystem of the inverse system
$\{A_0^{k(m,n)}\}_{n \in \mathbb {N}}$
forms a cofinal subsystem of the inverse system
![]() $\{A^j_0\}_{j \in \mathbb {N}}$
. In other words,
$\{A^j_0\}_{j \in \mathbb {N}}$
. In other words,
 $$ \begin{align*}{\varprojlim_{j \in \mathbb{N}}}^1 A^j_0 \cong {\varprojlim_{n \in \mathbb{N}}}^1 A^{k(m,n)}_0. \end{align*} $$
$$ \begin{align*}{\varprojlim_{j \in \mathbb{N}}}^1 A^j_0 \cong {\varprojlim_{n \in \mathbb{N}}}^1 A^{k(m,n)}_0. \end{align*} $$
Moreover,
![]() $\{\mathcal {A}^{\circ }/(\varpi ^r)\}_{n \in \mathbb {N}}$
is a constant inverse system. So we have
$\{\mathcal {A}^{\circ }/(\varpi ^r)\}_{n \in \mathbb {N}}$
is a constant inverse system. So we have
![]() ${\varprojlim _{j \in \mathbb {N}}}^1 \mathcal {A}^{\circ }/(\varpi ^r)=0$
and by applying the derived limits to the exact sequence:
${\varprojlim _{j \in \mathbb {N}}}^1 \mathcal {A}^{\circ }/(\varpi ^r)=0$
and by applying the derived limits to the exact sequence:
![]() $ 0 \to \{\mathcal {A}^{\circ }/(\varpi ^r)\}_{n \in \mathbb {N}} \to \{A_0^{k(m,n)}\}_{n \in \mathbb {N}} \to \{N_{k(m,n)}\}_{n \in \mathbb {N}} \to 0$
, we get an isomorphism:
$ 0 \to \{\mathcal {A}^{\circ }/(\varpi ^r)\}_{n \in \mathbb {N}} \to \{A_0^{k(m,n)}\}_{n \in \mathbb {N}} \to \{N_{k(m,n)}\}_{n \in \mathbb {N}} \to 0$
, we get an isomorphism:
 $$ \begin{align*}{\varprojlim_{j \in \mathbb{N}}}^1 A^j_0 \cong {\varprojlim_{n \in \mathbb{N}}}^1N_{k(m,n)}. \end{align*} $$
$$ \begin{align*}{\varprojlim_{j \in \mathbb{N}}}^1 A^j_0 \cong {\varprojlim_{n \in \mathbb{N}}}^1N_{k(m,n)}. \end{align*} $$
In particular, the right-hand side does not depend on the choice of
![]() $m \in \mathbb {N}$
. Now, we claim that
$m \in \mathbb {N}$
. Now, we claim that
 $$ \begin{align} g^{\frac{1}{p^m}} \cdot \big({\varprojlim_{n \in \mathbb{N}}}^1N_{k(m,n)}\big)=0. \end{align} $$
$$ \begin{align} g^{\frac{1}{p^m}} \cdot \big({\varprojlim_{n \in \mathbb{N}}}^1N_{k(m,n)}\big)=0. \end{align} $$
To prove this, we may replace the system
![]() $\{N_j\}_{j \in \mathbb {N}}$
with
$\{N_j\}_{j \in \mathbb {N}}$
with
![]() $\{N_{k(m,n)}\}_{n \in \mathbb {N}}$
to simplify the notation.
$\{N_{k(m,n)}\}_{n \in \mathbb {N}}$
to simplify the notation.
Choose any element
![]() $(\beta _i)_{i \in \mathbb {N}} \in \prod _{j \in \mathbb {N}}N_{j}$
and set
$(\beta _i)_{i \in \mathbb {N}} \in \prod _{j \in \mathbb {N}}N_{j}$
and set
![]() $\gamma _i:=g^{\frac {1}{p^m}} \beta _i$
. By using (8.3), the infinite sum
$\gamma _i:=g^{\frac {1}{p^m}} \beta _i$
. By using (8.3), the infinite sum
 $$ \begin{align*}\alpha_k:=\sum_{j=k}^{\infty} f_{j,k}(\gamma_j) \end{align*} $$
$$ \begin{align*}\alpha_k:=\sum_{j=k}^{\infty} f_{j,k}(\gamma_j) \end{align*} $$
makes sense, where
![]() $f_{j,k}:N_j \to N_k$
is the map given above. Then
$f_{j,k}:N_j \to N_k$
is the map given above. Then
![]() $(\alpha _k)_{k \in \mathbb {N}}$
maps to
$(\alpha _k)_{k \in \mathbb {N}}$
maps to
![]() $(\gamma _k)_{k \in \mathbb {N}}$
under the mapping:
$(\gamma _k)_{k \in \mathbb {N}}$
under the mapping:
 $$ \begin{align*}\Delta:\prod_{j \in \mathbb{N}}N_{j} \to \prod_{j \in \mathbb{N}}N_{j} \end{align*} $$
$$ \begin{align*}\Delta:\prod_{j \in \mathbb{N}}N_{j} \to \prod_{j \in \mathbb{N}}N_{j} \end{align*} $$
defined by the formula
![]() $\Delta ((x_i)_{i \in \mathbb {N}}):=\big (x_i-f_{i+1,i}(x_{i+1})\big )_{i \in \mathbb {N}}$
for
$\Delta ((x_i)_{i \in \mathbb {N}}):=\big (x_i-f_{i+1,i}(x_{i+1})\big )_{i \in \mathbb {N}}$
for
![]() $(x_i)_{i \in \mathbb {N}} \in \prod _{j \in \mathbb {N}}N_{j}$
, which gives (8.4). See [Reference Weibel62, Prop. 3.5.7] for the Mittag-Leffler condition and its relation to the derived inverse limits and [Reference Gabber and Ramero20, Lem. 2.4.2] for its almost variants. Since m was arbitrarily chosen, we conclude that
$(x_i)_{i \in \mathbb {N}} \in \prod _{j \in \mathbb {N}}N_{j}$
, which gives (8.4). See [Reference Weibel62, Prop. 3.5.7] for the Mittag-Leffler condition and its relation to the derived inverse limits and [Reference Gabber and Ramero20, Lem. 2.4.2] for its almost variants. Since m was arbitrarily chosen, we conclude that
![]() ${\varprojlim _{j \in \mathbb {N}}}^1 A^j_0$
is
${\varprojlim _{j \in \mathbb {N}}}^1 A^j_0$
is
![]() $(g)^{\frac {1}{p^{\infty }}}$
-almost zero, as desired.
$(g)^{\frac {1}{p^{\infty }}}$
-almost zero, as desired.
9 Appendix C: Almost Galois extensions
We make use of Galois theory of commutative rings in making reductions in steps of proofs of some results in the present article. Let
![]() $A \to B$
be a ring extension, and let G be a finite group acting on B as ring automorphisms.
$A \to B$
be a ring extension, and let G be a finite group acting on B as ring automorphisms.
Definition 9.1. We say that B is a G-Galois extension of A, if
![]() $A=B^G$
and the natural ring map
$A=B^G$
and the natural ring map
is an isomorphism.
Some fundamental results about Galois extensions are found in [Reference André1] or [Reference Ford18]. A source of the definition of almost G-Galois extension is [Reference André1]. Here, we cite some related results for the sake of readers.
Definition 9.2. Let
![]() $(A,I)$
be a basic setup, and let
$(A,I)$
be a basic setup, and let
![]() $B \to C$
be an A-algebra map with G acting on C as ring automorphisms. Then we say that
$B \to C$
be an A-algebra map with G acting on C as ring automorphisms. Then we say that
![]() $B \to C$
is an I-almost G-Galois extension if the natural map
$B \to C$
is an I-almost G-Galois extension if the natural map
![]() $B \to C$
induces an I-almost isomorphism
$B \to C$
induces an I-almost isomorphism
![]() $B \xrightarrow {\approx } C^G$
and
$B \xrightarrow {\approx } C^G$
and
is an I-almost isomorphism.
Proposition 9.3. Let
![]() $(A,I)$
be a basic setup, and let
$(A,I)$
be a basic setup, and let
![]() $B \to C$
be an A-algebra map with a finite group G acting on C such that
$B \to C$
be an A-algebra map with a finite group G acting on C such that
![]() $B \to C$
factors as
$B \to C$
factors as
![]() $B \to C^G \to C$
. Then the following assertions hold:
$B \to C^G \to C$
. Then the following assertions hold:
-
1. If
 $B \to C$
is I-almost G-Galois, then it is I-almost finite étale of constant rank
$B \to C$
is I-almost G-Galois, then it is I-almost finite étale of constant rank
 $|G|$
.
$|G|$
. -
2. Assume that
 $B \to D$
is an A-algebra map. Let G act on the base change
$B \to D$
is an A-algebra map. Let G act on the base change
 $D \otimes _B C$
through the second factor. If
$D \otimes _B C$
through the second factor. If
 $B \to C$
is I-almost G-Galois, then so is
$B \to C$
is I-almost G-Galois, then so is
 $D \to D \otimes _B C$
. Conversely, if D is faithfully flat over B and
$D \to D \otimes _B C$
. Conversely, if D is faithfully flat over B and
 $D \to D \otimes _B C$
is I-almost G-Galois, then so is
$D \to D \otimes _B C$
is I-almost G-Galois, then so is
 $B \to C$
.
$B \to C$
. -
3. Assume that
 $B \to C$
is I-almost G-Galois and assume that
$B \to C$
is I-almost G-Galois and assume that
 $B \to D \to C$
is a factorization of rings such that
$B \to D \to C$
is a factorization of rings such that
 $D \to C$
is I-almost H-Galois for a subgroup
$D \to C$
is I-almost H-Galois for a subgroup
 $H \subset G$
. Then the canonical map is an I-almost isomorphism and
$H \subset G$
. Then the canonical map is an I-almost isomorphism and $$ \begin{align*}D \otimes_B C \to \prod_{G/H} C \end{align*} $$
$$ \begin{align*}D \otimes_B C \to \prod_{G/H} C \end{align*} $$
 $B \to C$
is I-almost finite étale of constant rank
$B \to C$
is I-almost finite étale of constant rank
 $|G/H|$
.
$|G/H|$
.
Proof. See [Reference André1, Prop. 1.9.1] for the proof.
In the next lemma,
![]() $S_n$
will denote the group of permutations of n elements.
$S_n$
will denote the group of permutations of n elements.
Lemma 9.4. The following assertions hold:
-
1. Assume that
 $B \to C$
is étale of constant rank r. Then there is an
$B \to C$
is étale of constant rank r. Then there is an
 $S_r$
-Galois extension
$S_r$
-Galois extension
 $B \to D$
which factors as
$B \to D$
which factors as
 $B \to C \to D$
such that
$B \to C \to D$
such that
 $C \to D$
is an
$C \to D$
is an
 $S_{r-1}$
-Galois extension.
$S_{r-1}$
-Galois extension. -
2. Let C be a ring on which a finite group G acts as ring automorphisms. Set
 $B:=C^G$
. Suppose that there is a factorization
$B:=C^G$
. Suppose that there is a factorization
 $B \to D \to C$
such that
$B \to D \to C$
such that
 $G(D)=D$
and
$G(D)=D$
and
 $B \to D$
is a G-Galois extension. Then
$B \to D$
is a G-Galois extension. Then
 $D \to C$
is bijective.
$D \to C$
is bijective.
Proof. See [Reference André1, lemme 1.9.2 and 1.9.3] for the proof.
Acknowledgment
The authors are grateful to Professor K. Fujiwara for encouragement and comments on this article. They also thank S. Ishiro for helpful discussions. Finally, they thank the referee for a meticulous reading of the article.
Dedication
The present article is dedicated to our teachers, Professor Kazuhiro Fujiwara, and Professor Paul Roberts.